Colour Measurement and Mixture

The following are pairs of most carefully selected complementary colours of pigments, as adopted by Professor Church.

As these pairs of pigments are complementary, it follows that if rotated together in proper proportions, they should make a grey which will be indistinguishable from a grey formed by rotating black and white sectors together. (See chap. XV.)

It will probably happen that a good deal more of one of the pairs of the colours is required in the disc than of the other, and supposing that the two are each used of the full brightness which the pigments are capable of giving, it follows that in a diagram where equal areas are filled with the pigments as complementary, some means must be adopted to give the true depth of tone to each. The mixture of white will heighten the luminosity of either, or the admixture of black will lower it, but often alters the hue.

One of the most beautiful methods of observing complementary colours is by means of the polarization of light, which we need not describe in detail. What is known as Brücke's schistoscope is perhaps one of the most convenient. Dove's Iceland spar prism is also useful, when two pigments have to be worked on to paper, so as to be complementary. The two squares of pigmented paper are placed side by side, and two images of each are formed. One image of one colour can be caused to overlap the second of the other, and if the two when superposed appear of a grey they are complementary one to the other. If too much of one colour appears, it must be toned down till the grey is formed. This is a very simple piece of apparatus, and for experiments with pigments will be found to be very handy. When the right tint of each is secured in this manner, a further test may be made by making the pigmented surfaces into sectors, and rotating them together, when if the double-image prism gives correct results, the angular aperture of the sectors should be 180° each, to match a grey produced by a mixture by rotation of black and white.

We have already shown how the complementaries of the spectrum colours can be found; the question is can we find the complementaries of pigments by the spectrum? There is one very self-evident way. We can place the three slits in the spectrum as given in chapter IX., and match in intensity the white light of the reflected beam, and note the apertures of the slits. We must then in the reflected beam place the pigment whose complementary colour is required, and match its colour with the light from the three slits, keeping, for the sake of convenience, the white light falling on the pigmented surface of unaltered intensity, and again note the apertures. If we deduct the last measures from the first, the difference of aperture will give the complementary colour. Thus it was found that with slits in a certain position in the spectrum, to make white light the following apertures in hundredths of a millimetre were required:

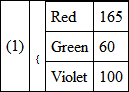
Emerald green was placed in the patch and was matched by the light from the three slits, when it was found that it required

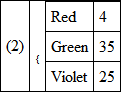
Deducting one from the other we get as the complementary colour,

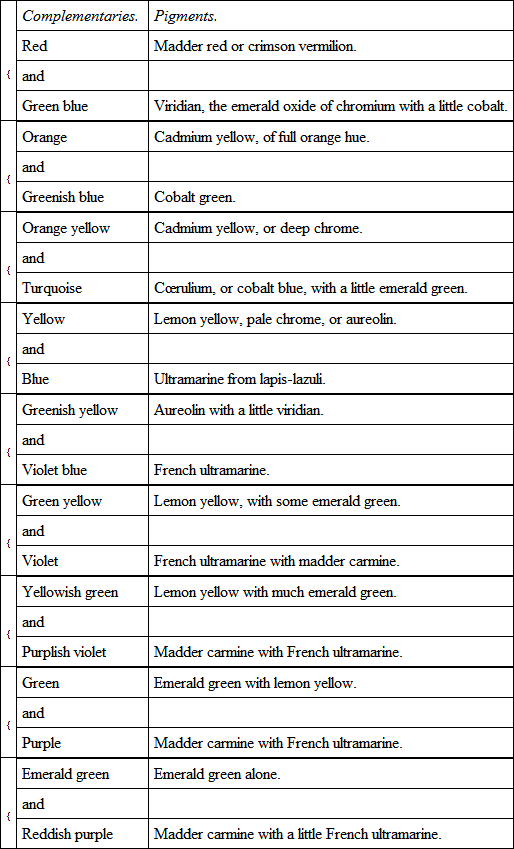
This is a complementary colour, but like the green itself it is mixed with white light; but we can easily deduce what is the simplest complementary colour; for we have only to deduct the possible white light from the second measure. Now evidently the greatest amount of white light is when the whole of the green is taken as forming part of it, with the proper proportions of red and violet, and these we can obtain by taking the proportions of the colours in (1); therefore deduct —

and this would leave as the complementary colour without any admixture of white —

which is a purple as would be expected.

Now to give the same dilution of white to the complementary that the emerald green has, we must take away from the emerald green all the white mixed with it, and add that quantity to the complementary. The white in the emerald green can be found by treating the whole of the red as going to form the white; we then have from (1) —

Deducting these from (2), we find that the colour of emerald green, less the white light, is 20·6 of green mixed with 1 of violet. To find the proper dilution of the complementary colour we must add the above proportions of the three colours, and as our final result we find the complementary colour, of equal impurity, is a mixture of —

The slits may be set at these apertures and a colour patch thrown on the screen, and we shall find it of a delicate pink. The truth of this can be seen by using a double-image prism to view the pigmented surface, illuminated by the same white light as that in which it was measured, and the colour patch on the screen by its side. The two colours may be caused to overlap, when it will be seen that white is produced.

Another example was an orange pigment, and this we will work out in the form of colour equation. The same mixture gave white, viz.:

165 R + 60 G + 100 V = W165 R + 42 G = O∴ the complementary colour, which isW – O = 18 G + 100 V,

or a dark-blue colour. In this case there was apparently no white light reflected from the orange. It was slightly glossy, and as polarized light was used for the reflected beam, it was probably somewhat quenched; but what is more probable is that the green contains some violet as well as red, for the reasons given in chapter XI. The reason we have been particular in showing to what extent complementary colours must be diluted with white to the same proportion that the colour itself is diluted, will be apparent if considered for a moment. A deep brown is in reality orange, much degraded in tone, and can be produced as a colour patch on the screen if a bright orange pigment be placed in the reflected beam of the colour patch, and the light nearly shut off by the rotating sectors. Now the same complementary colour will be found for both, but if we were to use the bright complementary colour which we obtained with the orange for the brown, and endeavoured to obtain a white with it by means of the double-image prism we should fail, as the complementary colour would predominate. Complementary colours can always be formed by a mixture of only two rays, and although the overlapping images may form white, yet when the two are placed side by side, it often will be found that the complementary, unless diluted with white, is evidently too dark to be satisfactory, but the luminosity may be increased by adding white to it, as any amount of white may be added to the mixture of the two rays which form the complementary, and of course white will still be formed with the original colour. It is thus quite feasible to give the complementary the same luminosity as the latter by adding white light to it. Like the colour itself, the complementary colour can always be expressed either by a single ray of the spectrum, or by white light from which a single ray is deducted. (See chapter XIII.)

CHAPTER XV

Persistence of Images on the Retina – The Use of Coloured Discs.

Fig. 39. – Disc to cause alternate opening and closing of two Slits.

By this time we must be thoroughly convinced that by throwing one coloured patch over another a compound colour can be formed; our next business is to demonstrate that the same effect can be produced by successive images of these same colours. Thus we can show that as a mixture of red and blue produces purple, when the two lights are superposed, so precisely the same purple can be produced by allowing the same two colours to strike the eye alternately, and in very rapid succession. We can make a match of the beautiful purple of permanganate of potash as before upon the screen, by placing one adjustable slit in the red and the other in the violet. If we place in front of the slits a disc cut out with equal angular apertures (Fig. 39), the slit S₁ will be covered when the slit S₂ is open, and vice versâ, and the two will never be uncovered at the same time when the card is turning round its centre. When this disc is caused to rotate rapidly, we shall have first a patch formed by the light coming through one slit, and then another formed by that coming through the other slit, thrown on the screen on the same place in rapid succession, and the effect on the eye should be precisely the same as if the disc was not there, save in the matter of intensity. Applying this artifice experimentally to the two slits which were used to give the colour of permanganate, the experiment tells us that such is the case. It would be going away from the intention of this work were the physiological aspect of this experiment dwelt upon; it need only be stated that an impression on the retina lasts an appreciable time, though short, and that the impression made by the blue patch has not had time to disappear before there is an impression made by the red patch, and so on. As the retina retains these two impressions together, they produce the impression of purple.

Fig. 40. – Disc painted Blue and Red.

For experiments in colour this duration of impressions is of great value, for we can take advantage of it to compound the colours of pigments together in a very simple manner. For instance, we can take a circular disc painted in sectors with blue and red (Fig. 40), and produce a purple by causing it to rotate round its centre. Small discs of two inches in diameter may be painted with different coloured sectors, and if a pin be passed through the centre, a smart movement of a finger at the periphery will cause it to rotate sufficiently quickly to make the colours blend. A more convenient plan for exact work is, however, to have an electro-motor similar to that which moves the rotating movable sectors (Fig. 41), and at the end of the spindle to fix a cap with a screw and nut attached. The disc, perforated at the centre with a clean-cut hole, can be slipt over the screw, and fastened by the circular nut. When the armature rotates, the disc also rotates at the same speed, and the colours thus blend without any exertion on the part of the observer. Ordinary tops can also be used, but it is somewhat fatiguing to have to wind them up and start them afresh for each experiment. The motor shown in the figure rotates sufficiently rapidly, with discs of eight inches in diameter, to blend colours. It may here be remarked that the stronger the light in which such sectors rotate, the quicker the rotation should be. Too slow a rotation allows a scintillation which is destructive of accuracy of reading. To blend some colours together also requires more rapid rotation than with others. The brighter the colour the more rapid it should be. We learn from this that the diminution of the more intense impressions on the retina is more rapid at first than of the feebler.

Fig. 41. – Electro-motor with Discs attached.

Fig. 42. – Method of cutting Disc to allow an overlap of a second Disc.

Very convenient discs for producing colours by rotation of sectors may be made by the following: vermilion (V), emerald green (E), French ultramarine blue (U), chrome yellow (Y), lamp-black (X), and (zinc) white (W). With these nearly every colour can be produced, or its value derived. The chrome yellow disc is somewhat superfluous, but is sometimes useful. The alteration in the proportions of the colours can be readily made by Clark-Maxwell's plan. From the circumference to the centre he cut the discs open, as at ab (Fig. 42). Any moderate number of discs, similarly cut, may be slipt over one another, and only a sector of each is left visible. It should be remarked that this necessitates the rotating apparatus being viewed with a direct light, as in the case of two or three overlapping discs it is impossible to keep them entirely flat, and shades are apt to be introduced. If we wish to produce a white, or rather a grey, from three colours, we can take three small discs of V, E and U, of equal diameter, and behind them place discs of black and white, of larger diameter, rotating the whole five on a common centre. We shall find that by altering the proportions of the three first we can get a grey which can be exactly matched by a mixture of black and white, X and W. It has already been shown that even lamp-black reflects a certain amount of white light, so this amount of reflected white light has to be added to the white in the outside sectors. In the sectors used in the following experiments it was found that the following proportions of the three colours were required —

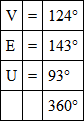
and to make the same grey it required

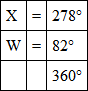
Now the black reflected 3·4 % of white light, so that really the proportions of black and white were

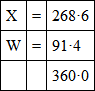
These matches were made in the light emitted by the crater of the positive pole of the electric light, and are correct only for this light. The greys here are dark greys, and such greys can be matched exactly by throwing the white light in which the comparisons were made on a white card, and reducing the intensity by means of the rotating sectors. We can prove whether our matches are fairly correct from our previous measures of the luminosity of these three colours, in comparison with that of white. The luminosities of V, E, and U, as found from the measures (pp. 93-95), are 36, 30, and 4·4, white being 100; 124 of V would have a luminosity of (124×36)/360, or 12·4; 143 of E would have 11·92; and 93 of U would have 1·14; which, added to either, give a luminosity of 25·46. The luminosity of 91·4/360 of white, which is that of the mixture of black and white, comes to 25·39, so that we may assume our observations have been fairly correct.

The influence of the kind of light in which the match was made is well exemplified by taking the matched discs whilst rotating into a room illuminated by the light from the sky, when it is seen that the grey of the outer discs is bluish; or again, if the matched discs be examined in gaslight, the inner grey will be found too blue.

The match of grey in this last light was found to be

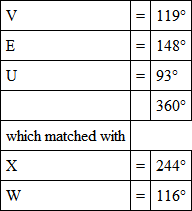
(In this case the black and white are the corrected black and white.)

The importance of making matches in a uniform light is fairly demonstrated by this experiment, and we cannot be wrong in asserting that as skylight and sunlight and cloudlight (the last being often a mixture of the two first), are so variable no measures made on one day can be fairly compared with those made on another, more especially if the observers are different. With an emerald green, a vermilion, an ultramarine, a white, and a black disc any colour may be reproduced in the rotation apparatus, the three first nearly matching what we have already stated to be the three primary colours.

It may seem curious that both black and white may have to be mixed with the colours, to produce a pigment colour; but a little reflection will show how it is. For instance, suppose we want to know the colour composition of gamboge (Y) in terms of vermilion (V), emerald green (E), and ultramarine blue (U). We must make a disc painted with gamboge, and also a black and a white disc of the same diameter, but rather larger than the other three discs, and place them on the spindle of the electro-motor (Fig. 43). We shall soon see on rotating them that no blue is required in the inner disc, and that all that remains to do is to use the red and the green. Mix these two, however, in whatever proportions we may, the mixture will never attain the same luminosity, consequently we must darken the yellow with black. Even then we shall find that, add what black we may, the rotating red and green sectors will always be a little less saturated with colour; which means that on rotation they produce a certain quantity of white light mixed with the yellow. This we might expect, for as emerald green, besides green and red, also contains a fair proportion of blue, and as red, green and blue when mixed give white, it follows that when V and E are rotated together, a grey or subdued white light must be mixed with the colour produced. Turning back to Chapter XIII. we also see that as the emerald green is expressible by a single ray of the spectrum, mixed with white light this result might have been foretold.

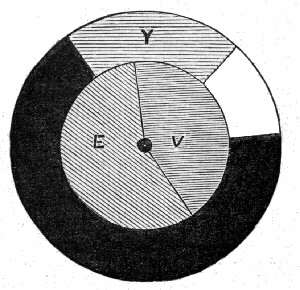
Fig. 43. – Arrangement to find value of Gamboge in terms of Emerald Green and Vermilion.

This necessitates adding some white to the rotating sectors of the yellow and black, as the yellow reflects but little white light, and finally we shall get an absolute match, of which the final results are

172 V + 188 E = 75 Y + 45 W + 240 X

This equation is full of meaning. It tells us in the first place what we have already known, that V and E are one or both impure colours, and that when rotated together in the proportions indicated, they produce at least a luminosity of white equal to 53/360 of a white disc (as the black used reflected just 3·4 % of white light). Further, it tells us that we can obtain the luminosity of Y, when we know the luminosities of V and E. At page 186, the luminosities of these colours are given as 36 and 30 respectively, white being 100. This makes the luminosity of the colours on the left hand of the equation 17·2 + 15·67, or 32·87, and on the right 75/360 Y + 14·76, and consequently the luminosity of Y = 86·9. In the same way we can obtain any other colour in terms of these standards.

We may here show how we can obtain the luminosity of any colour by means of the three inner discs, and the black and white outer discs. We have already shown that any colour may be matched by the combination of not more than two simple colours, after deducting white from it; and from this we deduce that any coloured pigment will form a grey with some two of the three coloured discs, V, E, and U; and this being done we can then calculate the luminosity. For instance, with an orange-coloured pigment we should proceed to make a disc of the same diameter as that of the three above; an inspection would show us that in this colour red predominates, and therefore we could do without the red disc. We should then alter the proportions of V, U, and O, till they gave a match which was the same as that of a grey given by the rotating black and white sectors.

In an experiment with an orange of this kind, the following results were obtained —

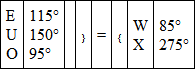
We can now from these deduce the luminosity of the orange employed in this case.

The luminosities of E and U, as already found, were 30 and 4·4, whilst the black (X) reflected 3·4 % of white light; we thus get the following equations —

115 × 30 + 150 × 4·4 + 95 O = (85 + 3·4 × 275) 100This gives 95 O = 9435 – (3450 + 660)O = 56

That is, the luminosity of the orange is ·56 that of white; by direct measurement it was ·57.

In a similar way the luminosity of chrome yellow (Y) is found. In this case —

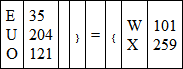
Similar equations were formed as the above.

35 × 30 + 204 × 4·4 + 121 Y = (101 + 3·4 × 259) 100whence Y = 77·6

That is, the luminosity of the chrome yellow is ·78; the same as was obtained by direct measurement.

In the same manner the luminosity of any colour can be found. Thus that of a purple, or of green, can be ascertained; of the former by using the green disc with either the red or the blue disc, and the latter by the red and blue disc. From this it is apparent that we can check the luminosities derived from other means by this plan.

A taking experiment can be made with colour discs to imitate all the colours of the spectrum in their proper order, though diluted more or less by white light. This can be done by rotating V, E, and U together; but in order to get additional luminosity in the yellow, we can use chrome yellow as well. If a disc be made as in the figure (Fig. 44), it will on rotating give a fair imitation of the spectrum, if it be viewed through a slit held in front of the disc.

Fig. 44. – Disc arranged to give approximately all the Spectrum Colours.

The mixture of colours by means of rotating sectors is one which the artist cannot use for artistic purposes, and it might seem that for him any deductions made from this method are useless; but it is not so. Suppose we take black lines ruled closely together on paper, and examine the surface from such a distance that the lines are no longer distinguishable it will appear of a grey; and if we take the amount of black on the paper and amount of white, and prepare two sectors of black and white, whose angles are in these proportions, and rotate them alongside the ruled surface, it will be found that the grey of one matches the grey of the other. If instead of lines of black and white we have them of light yellow and cobalt blue, a grey is also produced when the surface covered by the blue is to that covered by the yellow in correct proportions, and may be matched by rotating sectors containing merely black and white. Now some artists employ stippling, filling up cross-hatching of one colour with dots of a totally different colour, or they place dots side by side. When seen from the distance at which the picture should be viewed, these various colours blend one into another, and form a tint which is the same as that which would be obtained by rotating these colours together in the proportion in which they cover the ground. Artists, however, generally mix their pigments together on the palette, and the resulting mixtures are often totally unlike those which are obtained by rotating the same colours together, a noteworthy example is that of yellow and blue. By rotation, and when in proper proportion, these two give a white, but when mixed on the palette a green results. What causes this difference? Experimental proof is always the most satisfactory proof, so let us have recourse to the spectrum apparatus to obtain an answer. Let a spectrum be thrown on the screen, and in it place a strip of paper painted with the yellow, and then another with the blue. With the first it will be seen that the blue rays are not reflected, but only the green and yellow and red, taking the spectrum as roughly made up of these four colours. With the latter the yellow is not reflected, and but very little red, but the blue and the green are reflected strongly. Now we have already said that the reflection of colour from a surface is indicative of the colours the particles of pigments when taken thin enough to be transparent would transmit; hence we may take it that the yellow pigment transmits the red, yellow, and green, and the blue pigment scarcely anything but blue and green. When we have a mixture of these fine particles of pigment on paper, some will underlie the others. But let us pay attention to what would happen if a yellow particle were at the top, and a blue one beneath it. White light would impinge on the yellow particle, but only red, yellow, and green would pass out or be reflected from it. This sifted light would next fall on the blue particle and – as we have seen – only blue and green can pass through or be reflected from it; but as the yellow particle has already deprived the white light of its blue component, the green light alone would pass to the paper, and be reflected either direct from the surface of the paper, or through the particles themselves to the eye. If the blue particle were on the top, precisely the same effect would be produced; it would only allow blue and green to pass to the yellow particle, and as the yellow is opaque to the blue, only green light again would pass. Similarly if side by side the same phenomena would occur, since the light reflected from one on to the other would be deprived of all colour except the green. A very pretty experimental proof of this is to place a yellow solution of dye in front of the slit of the colour apparatus, and having formed the yellow colour patch to place in it a piece of paper covered with a blue pigment: the latter becomes green. By placing a blue solution in front of the slit, and using a piece of yellow pigmented paper, the same result is obtained. The artist therefore in mixing his pigments calls into play the law of absorption, and from his mixtures very naturally assumes that blue and yellow make green. He makes a neutral tint of blue, red, and yellow, and as the red cuts off the green, this naturally follows from the above. Such experiments as these led him to the conclusion that red, yellow, and blue are the three primary colours, an assumption which had he used simple spectrum colours instead of compound colours, such as pigments, he would not have ventured to make.