Colour Measurement and Mixture

10(34) = 20(35) + 5(28)or (34) = 2(35) + ¼(28)

which means that the colour sensation at (34) is made up of two parts of the sensation of (35), together with ¼ part of the sensation of (28).

In the same way we find that the colour sensation of (18) is made up of the sensations of (17) and (28).

(18) = 4(17) + 1/10(28)

In this way all the different colour sensations can be referred to the sensations which we may happen to consider as best representing the fundamental sensations. What these are is a matter still unsettled; though from the equations formed by colour-blind people, who only require really two colours to form equations, their places are approximately known; evidently as before said, the ray in the spectrum which the green colour-blind person sees as white light, is that where to the normal eye the green fundamental sensation is purest, being free from predominance of either of the other two sensations, and might be taken as a standard colour. Now if our luminosity curve is correct, and if the sum of the luminosities of each colour separately is equal to the luminosity of the colours when mixed (which we have shown to be the case in chapter VII.), it follows that the correctness of the measures can be checked by using the widths of the slits as multipliers of the luminosities. These luminosities can then be added together, and they should equal in luminosity the white light with which the comparison was made. The results can be compared together by reducing the equations to the same standard of white light.

The following is a set of observations which bear this out.

The red and violet slits in this case were kept at 35 and 17·8 on the scale, and the position of the green slit altered.

The red slit was at a point in the spectrum between C and the red lithium line, and excited probably the fundamental sensation of red alone. The violet slit was close to G, and probably in this case the fundamental sensation of violet was almost excited alone. With the green slit the reverse was the case, all three fundamental sensations being excited. At 26·3 the green sensation was probably the fundamental sensation mixed with white light alone, as at that point the green blind person saw white light in the spectrum, on the red side of it there being what he describes as a warm colour, and on the violet side a cold colour.

An inspection of the table will show how very closely the sum of the luminosities agree amongst themselves, the white light formed by them in each case being of equal intensities. It must be recollected that white light is not necessary to form colour equations; colours may be mixed to form any other colour, which may be taken as a standard. This is often useful in the case of the light between the violet and the blue, where the luminosities are small compared with the luminosity in the green, yellow, and red.

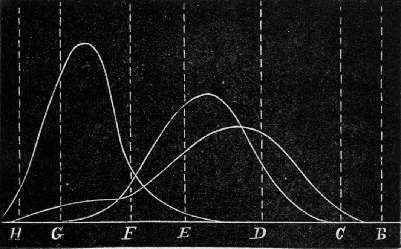
Fig. 35. – Kœnig's Curves of Colour Sensations.

By taking a large number of colour equations, Kœnig, who works in Helmholtz's laboratory, has derived what he considers curves of the three fundamental sensations in a normal-eyed person, and also those of the colour-blind. It may be said that with the colour-blind only two of the fundamental sensations are seen, and therefore only two curves are found, and that these agree in the main with some two of the curves of the three belonging to the normal-eyed.

Fig. 36. Maxwell's Colour-box.

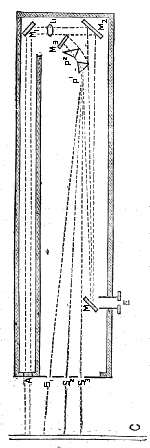
Maxwell was the first to make a definite piece of apparatus for the purpose of obtaining colour equations, and we reproduce from his paper in the Philosophical Transactions of the Royal Society for 18 – , a somewhat modified diagram of it.

This apparatus is often known as Maxwell's colour-box, and is in fact a spectroscope reversed. With a collimator and prisms we form a spectrum on the focusing-screen of the camera (Fig. 6), by light coming through the slit, and we can obtain light on the distant screen, a patch of any colour, by placing in the spectrum slits as given at Fig. 30. If we were to illuminate the slits so placed with white light, and look through the slit of the collimator, we should see the front surface of the first prism illuminated by the mixture of the colours which would, when the light illuminated the collimator slit, have formed one colour patch on the screen. In Maxwell's apparatus, the slits S₁, S₂, S₃ are illuminated by the light reflected from a white card C, placed in the sunshine, the rays passing through them fall on two prisms P₁, P₂, are reflected back again through these prisms by a concave mirror M₃, are received on another mirror M, and fall at E on to the eye. At A is an aperture in the box, letting through white light on to a mirror M₁, which reflects it through a lens L on to M₂, which again reflects it on to M, and so to the eye at E. Thus at E an image of the prisms, and an image of the aperture are seen, and the white light of the latter can be compared with the mixture of the colours formed by the prism passing through S₁, S₂, and S₃.

Suppose we have one slit S₁, the white light will be decomposed by the prisms, and will be seen at E as light of the same colour as would be seen at S₁, if the light were sent from E to S₁, and so with the other slits. Thus when two or three of the slits are uncovered, the light falling on the eye at E will be a mixture of two or three colours.

There are two drawbacks to the mode of illumination used, one being that the quality of sunlight varies, and therefore colour equations will not be accurately comparable one with the other; and the second is that the light reflected from the card is not absolutely the same in all directions, and it cannot be perpendicularly placed to each of the rays which strike the prisms, after passing through the different slits. This latter is a small objection, and is not of much account, but the first drawback is a more serious one.

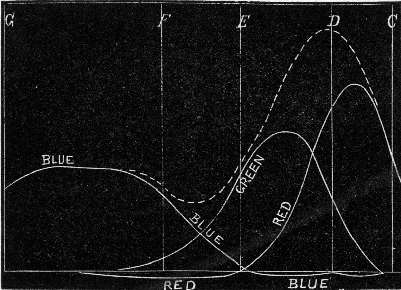
Fig. 37. – Maxwell's Curves of Colour Sensations.

With this apparatus, then, Maxwell formed his colour equations, but he fixed as the colours which may be called his standard colours, portions of the spectrum which are certainly not pure, and hence he got curves which are not as perfect as those of Kœnig.

It will be seen, for instance, that his red and violet curves do not overlap, but touch each other near E. Were this true, the green colour-blind person should see a dark space in the spectrum, since the green sensation is missing in such eyes. As a matter of fact the luminosity of the spectrum is very considerable to such a person at this point.

It will also be seen that some of his curves are negative curves lying below the base. This shows that the three standard colours he took are somewhat wrong. The dotted curve gives the combination of his three sensations at every point, and should be the luminosity curve; but owing to his having taken empirically certain standards of luminosity for his three colours, it does not represent the truth, as may be seen on comparison with Fig. 11, page 79.

It must be recollected that since Maxwell's observations the subject has been largely experimented upon, and naturally improved appliances and greater knowledge have enabled more nearly correct views to be entertained regarding it.

CHAPTER XIII

Match of Compound Colours with Simple Colours – All Colours reduced to Numbers – Method of matching a Colour with a Spectrum Colour and White Light.

If we place the solution of bichromate of potassium in front of the slit of the collimator, we shall see that on producing a spectrum on the screen, all rays from the red to the yellow-green pass; hence bichromate of potash transmits a colour which is a compound colour.

It has been shown that this orange colour and the spectral yellow can be matched by mixing the simple colours of red and green together; but it will be instructive to see if a simple colour in the spectrum itself can be found which can match such a compound colour as that of the bichromate.

If we place the bichromate in the reflected beam of the colour patch apparatus and illuminate one shadow cast by the rod with the light transmitted by it, and pass a slit along the spectrum, to produce monochromatic light, with which the other shadow of the rod is illuminated, a position will be found near the orange sodium line "D," where the two colours apparently match in every respect; when the intensities of the two illuminated shadows are equalized as before by the rotating sectors. In the same way by filling the part of the square with the pigment on which the shadow illuminated by the reflected beam falls, we can see if we can match emerald green, cyanine blue, and other coloured pigments.

It will often be – more often than not – necessary, however, to dilute the spectrum colour thrown on the white half of the patch with a trace of white light. By reference to our previous experiments we arrive at what may appear an unlooked-for result, that no matter what the colour may be, we can refer it to one ray of the spectrum, together with a percentage of added white light. It is worthy of remark, that the place in the spectrum where the simple and the compound colours match, varies according to the kind of light with which the pigment is illuminated. This we can show in a very simple way.

To persons who are totally colour-blind to one sensation, viz. the green or the red, the matching of a compound colour with a simple one in the spectrum should possess no difficulties. Taking the trichromic theory of three sensations for the normal-eyed person, it is evident that only the following classes of sensations are possible in the normal-eyed, the green colour-blind and the red colour-blind —

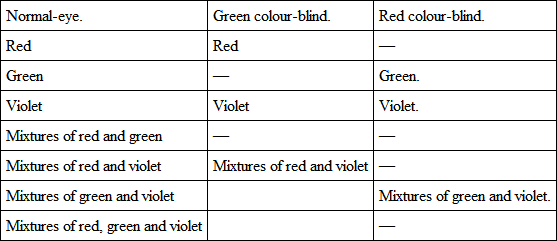
If we take as a type of colour-blindness the green colour-blind person, we see that every colour in the spectrum must be either pure red or violet, or else these colours mixed with more or less white light, since these two sensations when excited in certain proportions give the sensation of white. At one place, which is commonly called the neutral point, the proportions of the two colours are such that the impression there given is only white; hence it follows that, between this neutral point and each end of the spectrum, the rays are mixtures of violet and white, or red and white, the dilution of the colours varying from no white to all white. As every compound colour must be a mixture of the same two colours in certain proportions, it follows that the green colour-blind person can match every compound colour with some one ray of the spectrum, and that every colour must to him be either red or violet, diluted with different proportions of white light.

In the same way, a person who is colour-blind to the red can also match any colour with a single spectrum colour, and he will see it as green or violet diluted with more or less white light. This can be readily understood, but it is not quite so plain how any colour sensation felt by the normal eye can be referred to the spectrum.

If we take three rays in the spectrum – one in the red between C and the red Lithium line which we will call R, another in the green between F and b which we will call G, and a third in the violet near G but on the H side of it, and which we may call V– then by varying their intensities (which is equivalent to varying the luminosities) and mixing them, we can give the same impression to the eye that any compound colour gives; and that any intermediate simple spectrum colour gives, if very slightly diluted with white light. With these same three colours, but in different proportions, we can also give the impression of white light to the eye. The intermediate spectrum colours between the green and the violet rays selected when slightly diluted are imitated by mixing these rays together in different proportions, and similarly those lying between the red and the green by mixing together these rays in different proportions – and there is some ray present in the spectrum which, when very slightly diluted with white light, has the same colorific effect on the eye as the mixtures of the pairs v and b, and G and R, in any proportions whatever.

Let the luminosities of the rays R, G and V, which give the impression of white light, be a, b and c units respectively, and p, q and r those which give that of the colour which has to be registered and reproduced. We then get the following equations – where W is white, w its luminosity, Z the colour, and z its luminosity —

aR + bG + cV = wW– (i.); pR + qG + rV = zZ– (ii.);

Then evidently —

(a + b + c) = w; and (p + q + r) = zLet p = ɑa, q = βb, r = ɣc,

Then we may write (ii.) as —

αaR + βbG + ɣcV = zZ– (iii.)

Now either ɑ, β, or ɣ must be smaller than the other two. As an example, if ɑ be the smallest, we multiply (i.) by ɑ when we get —

ɑaR + ɑbG + ɑcV= ɑwW– (iv.)Subtracting (iv.) from (iii.) and we get —(β-ɑ)bG + (ɣ-ɑ)cV = zZ – ɑwW

Now it has already been stated that between V and G there is some ray which gives the same sensation of colour, mixed with a very small quantity of white light, as the above mixture of V and G– let us call it X and its luminosity x [x being evidently equal to (β-ɑ)b + (ɣ-ɑ)c], and μ the luminosity of the small quantity of white added.

We then get zZ = xX + (μ + ɑ) W.

Here we have the colour Z in terms of a single ray, and of white light.

This same holds good when in (ii.) ɣ is smaller than ɑ and β; but it does not do so should it happen that β is the smallest, for there is no part of the spectrum which contains simple colours giving the same sensation to the eye as mixtures of red and blue. There is, however, a very simple way in which the registration of such a colour (which it must be remarked must be of a purple tone) can be effected. It can be fixed by its complementary. To do this we must add to (ii.) a certain amount of R and V, which will make the whole white. Thus, suppose in (iii.) ɑ to be larger than ɣ and ɣ than β, then we must add ϕbG + θcV and we have

ɑaR + (β + ϕ)bG + (ɣ + θ)cV = nW = Z + ϕbG + θcV;but (β + ϕ), and (ɣ + θ) each equal ɑ ∴ n = ɑw∴ Z + ϕbG + θcV= ɑwW

Now between V and G in the spectrum there is some single colour which gives the sensation of the mixture of G and V. Let it be X´ with luminosity x´, together with white whose luminosity is μ´, which must equal (ϕb + θc).

∴ Z + x´X´ + μ´W = ɑwW Z = (ɑw – μ´)W – x´X´

which again is the colour expressed in terms of white light less the complementary colour. We have thus arrived at the very simple deduction that the hue and luminosity of any colour, however compounded, may be registered by a reference to white light and a single ray of the spectrum.

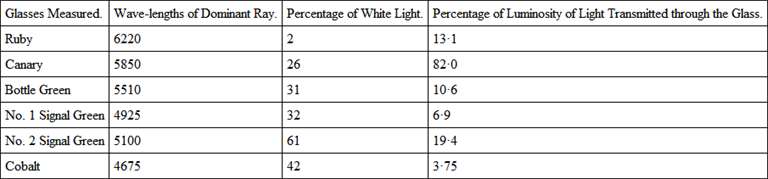
In practice this dominant ray is very easy to find. Suppose we wish to determine numerically the colour of a signal-green glass in the electric light, we should proceed as follows —

The colour patch apparatus (described in chapter IV.) is employed, and the coloured glass is placed between the silvered mirror which reflects the beam already reflected from the first surface of the first prism of the spectrum apparatus, and the screen, and a square image of that surface of the prism showing the tint of the glass is formed on the screen by means of the lens. Touching this image is a square patch of white light formed by the re-combination of the spectrum by means of another lens. An opaque slide containing an adjustable slit is moved across the spectrum in the manner described in the chapter referred to until the colour of this last patch is approximately the same hue as that of the glass.

In the path of the reflected beam, but between the prism and the silvered mirror, is inserted a piece of plain glass which can be made to reflect part of the beam into the spectrum patch of light, a square patch of the white light being formed by means of a third lens. We thus have monochromatic light mixed with white light. The requisite intensity of the added white light can be adjusted by means of the rotating sectors, as described in the same chapter, which open and close at will during rotation, and the total luminosity of the mixed beams can be altered by this, together with the adjustable slit in the slide. The slit may probably have to be moved in the spectrum to make the hue of these mixed lights the same as that of the glass, but by trial the position of the ray whose colour when diluted with white makes the match is readily found. The position of the slit in the spectrum is noted, as also the aperture of the sectors. The relative luminosities of the beam reflected from the plain glass mirror and of the coloured ray is next measured by placing a rod in the path of the two beams, and equalizing by the sectors the luminosity of the shadows which are illuminated, the one by the spectral ray, and the other by the white light. When the sector aperture is noted the registration is complete, as far as hue is concerned, but the luminosity of the ray transmitted through the glass should be compared with that of the reflected beam, and then the luminosity is also recorded.

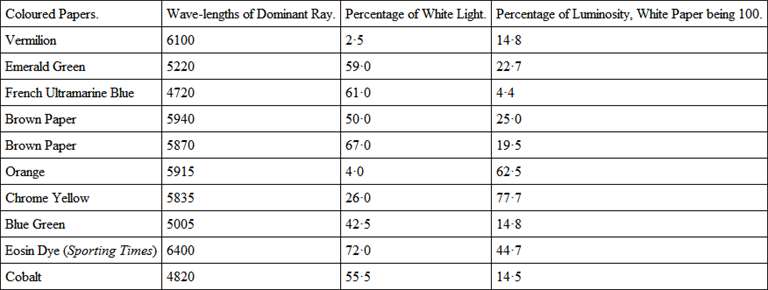
Should the colour of a pigment be in question, the ray reflected from the silvered mirror is made to fall on the pigmented surface and the same procedure adopted.

If a purple glass (say) has to be registered, we proceed in a slightly different manner. The patch of coloured light passing through the purple glass is superposed over the spectrum patch, and the slit in the slide is moved till a ray is found which will make white light when superposed on the colour of the glass. The luminosities of this white light, of the reflected beam, and of the spectral colour are compared "inter se," and there are then sufficient data with which to make numerical registration.

Coloured glasses to be used at night with oil or gas, or pigments to be viewed by these lights, must be registered in these lights. As the spectrum colours are always the same, it is convenient to use the electric light spectrum, and the only alteration in the apparatus is to use two gas-lights to illuminate two square apertures, in front of one of which the glass whose colour has to be measured is placed. The images of these apertures are thrown on the screen, the coloured image touching the square image of the spectral colour patch, and the naked image over the latter. The same determinations are gone through as those just described.

The following are the determinations of some glasses —

The following are determinations of some coloured pigments —

CHAPTER XIV

Complementary Colours – Complementary Pigment Colours – Measurement of Complementary Colours.

We are now in a position to enter into the question of complementary colours, which is one of supreme interest to artists. A complementary colour, in its strictest sense, may be described as the colour which, combined with the colour whose complement is required, makes up white. In this definition we have three characteristics to take into account, viz. hue and luminosity, and dilution with white light. As an example of what we mean we refer to an experiment which was made and described at page 125. It was said that if the violet slit was placed in a certain position in the blue of the spectrum, it was possible to move the green slit into a part of the yellow, so that the two colours when mixed together would form white. In that case the blue is complementary to the yellow, and the yellow to the blue, so long as the intensities are those which make up white light. Again, if it requires the light coming through the three slits to make up white light, be it the white of the electric light or that of gaslight, we can obtain the complementary colour of the light issuing through any one of them by covering that slit up. Thus suppose the slits to be in the normal position the complementary colour of the red is a green-blue, formed by the mixture of the violet and green rays, the complementary colour of the green is a purple, formed by the mixture of the red and the violet light, whilst the complementary colour of the violet is greenish yellow, formed by the mixture of the red and green rays. It will be evident that as the intensities of the three rays respectively will be different according as the white light matched is the electric light or gaslight, the complementary colours in the former will be different in hue and intensity to those in the latter.

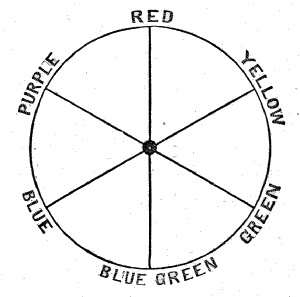
Fig. 38. – Chromatic Circle.

Another couple of striking experiments which the writer devised to show these colours can be made with the colour patch apparatus, and on the same principle as that used for obtaining the intensity of the rays reflected from pigments, and transmitted through coloured transparent bodies. Instead of the small slit with a right-angled prism in front to deflect the beam from the top spectrum, where two spectra are produced (see Fig. 16, p. 95), a single spectrum is used, with a right-angled prism of such a size that it deflects half of it, which is again reflected on to the screen by a mirror, and through a lens to form a second patch of equal size as the undeflected beam. A rod can be so placed in the path of the beams that two coloured stripes are formed, together with a white stripe caused by their overlapping. The two coloured stripes are complementary one to the other. By moving the prism along the spectrum various coloured stripes can be formed, in some cases one being much less luminous than the other, and yet they are complementary. If instead of the large right-angled prism a smaller one be used, the complementary colour due to a small part of the spectrum can be shown in the same manner.

It is customary to show the complementary colours diagrammatically by what is known as the chromatic circle. Roughly it is drawn as in the above figure (Fig. 38). The three colours, red, green and blue, which are taken for primary colours, are placed at 120° apart in a circle, and lines drawn from them through the centre, at which white is supposed to be situated. Where these lines cut the circumference is placed the complementary colour. Other colours can be placed round the circle with their complementary colours opposite, and so a fairly complete diagram of the spectrum can be made. But it must be remembered that this is really of no scientific value, as it conveys no idea of the luminosity of the spectrum colours, nor of the quantities which have to be mixed together to form the complementaries. Such a circle is, however, convenient as a sort of memoria technica, and can be filled up according to the fancy of the observer.