
Полная версия
Математические модели в естественнонаучном образовании. Том II
5.4.5. Для первого дерева на рисунке 5.23 рассчитайте минимальное количество требуемых изменений базы, разметив внутренние вершины по алгоритму из предыдущего раздела. Затем покажите, что второе дерево требует точно такого же количества изменений основания, даже если это не согласуется с тем, как обозначили внутренние вершины на первом дереве. Основной вывод, к которому нужно прийти после решения этой задачи заключается в том, что алгоритм, который используется для подсчета минимального количества изменений базы, необходимых для дерева, не обязательно покажет все способы, которыми можно достигнуть минимума.
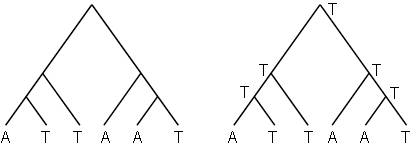
Рисунок 5.23. Деревья для задачи 5.4.5.
5.4.6. Если приведены последовательности для 3 терминальных таксонов, то информативных сайтов быть не может. Объясните, почему это так, и почему это не имеет значения.
5.4.7. Основания на определенном участке в выровненных последовательностях из разных таксонов образуют закономерность. Например, при сравнении
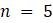
а. Объясните, почему при сравнении последовательностей для
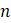
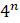
б. Некоторые шаблоны неинформативны. Простыми примерами являются четыре паттерна, показывающие одно и то же основание во всех последовательностях. Объясните, почему существуют
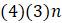
в. Сколько всего существует неинформативных шаблонов, в которых 2 основания появляются один раз, а все остальные совпадают?
г. Сколько существует неинформативных шаблонов, в которых 3 основания появляется один раз, а все остальные согласованы?
д. Объедините свои ответы, чтобы рассчитать количество информативных шаблонов для
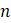
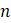
5.4.8. Компьютерная программа, вычисляющая оценки экономии, может работать следующим образом: сначала сравните последовательности и подсчитайте количество сайтов
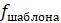
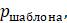
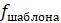
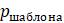
5.4.9. Показатели экономичности можно рассчитать еще эффективнее, используя тот факт, что несколько разных шаблонов всегда дают одинаковую оценку. Например, при сопоставлении 4 таксонов шаблоны (ATTA) и (CAAC) будут иметь одинаковую оценку.
а. Используя это наблюдение для 4 таксонов определите, сколько различных информативных таблиц должно быть рассмотрено, чтобы получить оценку экономии для всех возможных комбинаций?
б. Повторите часть (а) для 5 таксонов.
5.4.10. Используйте метод максимальной экономии для построения некорневого дерева для моделируемых последовательностей a1, a2, a3 и a4 в файле данных seqdata.mat. Сначала поместите последовательности в строки массива командой a=[a1;a2;a3;a4]. Затем найдите информативные сайты самостоятельно запрограммированной функцией infosites=informative(a). Наконец, извлеките информативные сайты с помощью команды ainfo=a(:,infosites).
а. Каков процент информативных сайтов?
б. Сколько различных деревьев следует проанализировать, чтобы найти самое экономное, относящееся к четырем таксонам?
в. Бывает слишком сложно использовать все информативные сайты для ручного расчета. Если это так, то используйте хотя бы первые 10 информативных сайтов, чтобы выбрать самое экономное дерево.
г. Согласуется ли найденное дерево топологически с тем, которое получается методом UPGMA и/или методом присоединения соседей с использованием расстояния Джукса-Кантора?
5.4.11. В этой задаче попытайтесь использовать метод максимальной экономии для построения некорневого дерева для ранее смоделированных последовательностей d1, d2, d3, d4, d5 и d6 в файле данных seqdata.mat. Начните с поиска информативных сайтов, как в предыдущей задаче.
а. Каков процент информативных сайтов?
б. Вычислите количество некорневых деревьев, которые необходимо изучить, если рассматривать все комбинации.
в. Используйте метод присоединения соседей, с логарифмическим расстоянием, вычисляемым из полных последовательностей, чтобы получить дерево, которое является хорошей отправной точкой для поиска наиболее экономных. Рассчитайте его оценку экономии, используя только первые 10 информативных сайтов.
г. Опять же, используя только первые 10 информативных сайтов, найдите по крайней мере 4 других дерева, которые похожи на одно из части (в). Можно ли найти более экономные?
д. Насколько уверены в том, что самое экономное дерево, которое нашли, действительно является самым экономным из всех возможных комбинаций? Для какого процента возможных деревьев вычислили оценки экономии? Какой процент информативных сайтов использовали?
5.5. Другие методы
На самом деле существует много других подходов к построению филогенетического дерева. Список предлагаемых методов довольно длинный и с каждым годом становится все длиннее, так как исследователи продолжают развивать данную проблематику.
В дополнение к дистанционным методам и методу максимальной экономии существует третий основной класс подходов, называемых методами максимального правдоподобия. Идея метода максимального правдоподобия состоит в том, что сначала предстоит выбрать конкретную модель молекулярной эволюции, например, модель Джукса-Кантора, 2- или 3-параметрическую модель Кимуры или более сложную. Затем нужно рассмотреть конкретное дерево, которое является кандидатом для описания связи данных таксонов. Предполагая, что эволюционная модель и конкретное дерево верны, можно рассчитать вероятность того, что последовательность ДНК могла быть получена именно на этих исходных данных. Вычисляется вероятность дерева, охватывающего имеющиеся данные. Повторяем этот процесс на всех остальных деревьях, получая значение вероятности для каждого. Затем выбираем дерево, к которого получилась наибольшая вероятность, поскольку именно такое дерево, как оказалось, лучше всего соответствует имеющимся данным.
Для многих исследователей методы максимального правдоподобия, которые следуют давней традиции в математической статистике, дают наибольшую надежду на то, что построенное дерево получилось хорошим. Однако можно столкнуться с рядом проблем. Во-первых, вычисляемые вероятности зависят от выбора конкретной модели эволюции, и если эта модель плохо описывает реальный процесс, то можно поставить под сомнение достоверность результатов. Во-вторых, как и в случае с экономностью, метод требует рассмотрения всех возможных деревьев, а значит, больших вычислительных затрат. Для каждой рассматриваемой топологии дерева требуется громоздкий расчет, чтобы найти оптимальные параметры модели, согласующиеся с данными. Если количество таксонов велико, то невозможно перебрать все возможные деревья, оптимизируя параметры модели для каждого, поэтому на практике используются эвристические методы сокращения числа свободных переменных. Хотя с практической точки зрения кажется, что данные методы работают хорошо, максимизация вероятности требует гораздо больше вычислительных ресурсов, чем другие подходы.
Другой способ классификации методов построения филогенетических деревьев состоит в том, чтобы разделить их на два класса: те, которые выбирают дерево на основе некоторого критерия оптимальности, и те, которые представляют собой алгоритмы, создающие дерево. Метод максимальной экономии и метод максимального правдоподобия основаны на критериях оптимальности, тогда как обсуждаемые ранее дистанционные методы являются алгоритмическими. Некоторые исследователи утверждают, что методы имеющие критерии оптимальности по своей сути превосходны, потому что они, по крайней мере, ясно указывают, на чем основан выбор дерева. Однако, поскольку поиск оптимального из большого числа деревьев может оказаться невыполнимым с вычислительной точки зрения, компьютерные реализации методов экономии и правдоподобия иногда начинаются с рассмотрения деревьев, созданных алгоритмическим методом, например, методом присоединение соседей, или одного из его вариантов, полученного путем циклического перемещения нескольких веток исходного дерева.
Одна из трудностей выбора оптимального метода для использования заключается в том, что можно найти хорошие аргументы за и против любого из методов. Тем не менее, необходимость строить деревья для исследования биологических проблем слишком велика, чтобы можно было не использовать существующие методы, а ожидать появления новых. Достаточно разумный подход заключается в том, чтобы всегда использовать несколько различных методов для имеющихся данных. Вместо того, чтобы доверять одному методу, для получения точного дерева, посмотрите, дают ли разные методы примерно одинаковые результаты. Они часто это делают и если используемые методы этого не делают, то стоит выяснить, почему такое происходит. Недостаточно просто запустить компьютерную программу на имеющихся данных и принять получившееся дерево как истинное.
Даже когда дерево уже выбрано тем или иным методом, было бы желательно дать количественную оценку, насколько можно быть уверенным в правильности выбора. Частичный ответ на этот вопрос может дать статистический метод самопроверки, – бутстрэппинга, что буквально означает «подтягивание за ремешки обуви». В процедуре самопроверки истинные последовательности данных используются для создания набора новых, псевдореплицированных последовательностей той же длины. Основания в конкретном сайте для генерации новых последовательностей выбираются с той же вероятностью какую имели основания, появляющиеся в случайно выбранном сайте в исходных последовательностях. Таким образом будет построено и записано дерево для филогении псевдорепликантов. Затем эта процедура повторяется много раз, что дает большую коллекцию подобных деревьев. Если достаточно высокий процент получаемых таким способом деревьев согласуется с первоначальным деревом, полученным с использованием исходных данных, то можем быть уверены в истинности проверяемого дерева.
Однако важным предостережением при использовании вышеописанного метода является то, что этот метод помогает только оценить влияние изменчивости в последовательностях на построение дерева. Данный метод ничего не говорит о фундаментальной обоснованности алгоритма, с помощью которого выбирается дерево – он только указывает, как изменчивость данных могла повлиять на результат.
На большом количестве таксонов настоятельно рекомендуется использовать специализированное компьютерное программное обеспечение для использования любого из упомянутых методов. Двумя широко используемыми пакетами, реализующими различные методы, являются PAUP* (Суоффорд, 2002) и PHYLIP (Фельзенштейн, 1993). Если вдруг когда-нибудь получите доступ к любому из них, то стоит изучить их возможности.
5.6. Приложения и перспективы
Вернемся к вопросу о гоминоидной филогении, который звучал по введении в эту главу. Какое дерево можно вывести из данных митохондриальной ДНК? Хотя можно было бы прочитать ответ в специализированной литературе, но предпочтительно, если найдете его самостоятельно. В упражнениях ниже будет возможность применить некоторые методы пройденной главы к данным, начиная либо с необработанных последовательностей, либо с некоторых расстояний, уже вычисленных из последовательностей.
Анализ данных, который впервые выполнил Хаясака с соавторами в 1988 году опирается в первую очередь на использование алгоритма присоединения соседей, как и анализ, который можно легко осуществить с помощью MATLAB. Если есть доступ к специализированному программному обеспечению, предназначенному для применения метода максимальной экономии, максимального правдоподобия или других методов, то настоятельно рекомендуется посмотреть, дают ли эти методы аналогичные результаты.
Кроме того, имейте в виду, что анализ, который делаете, всегда основан лишь на одном конкретном участке ДНК. Исследования, основанные на других ортологичных последовательностях, могут дать разные результаты. Кроме того, существует много подходов к филогенетическому выводу, которые не основаны на последовательностях. Должны быть скрупулёзно изучены доказательства адекватности каждого из используемых методов, прежде чем делать сильные заявления о филогении гоминоидов.
По мере развития методов построения филогенетического дерева из данных последовательности ДНК они были использованы и для изучения ряда других интересных вопросов. Даже беглый обзор высокорейтингового исследовательского журнала, такого как Science, обнаруживает большое количество статей, в которых генетические последовательности используются для исследования эволюции различных видов от общего предка. Вот лишь несколько примеров некоторых недавних приложений.
1. Исследование того, параллельна ли эволюция нескольких видов друг другу: например, эволюцию хозяев и паразитов можно изучить, построив отдельные филогенетические деревья для каждого из них. Сходство топологий деревьев может указывать на то, эволюционировали ли паразиты вместе с хозяином, или паразиты «перепрыгнули» от одного вида хозяина к другому, изучал Хафнер в 1994 году. Аналогичным образом, деревья для двух симбиотических видов, таких как муравьи, растущие грибы и грибы, которые они выращивают, помогают указать, как далеко в эволюционной истории простирается симбиотическое партнерство. Эти вопросы изучали Чапел и Хинкл в 1994.
2. Определение вероятных источников инфекции вируса иммунодефицита человека (ВИЧ) путем построения деревьев из последовательностей ВИЧ у ряда инфицированных лиц: Было несколько судебно-медицинских применений этого, к случаям СПИДа во Флориде, как следует из публикаций Альтмана 1994 года и Оу 1992 года, а так же их приложения к делу врача, обвиняемого в умышленном введении ВИЧ бывшему любовнику, исследовал Фогель в серии работ 1997 и 1998 годов.
3. Изучением того, вошли ли гены в геном определённого вида через латеральный перенос занимались Андерссон и Зальцберг в 2001 году: когда дерево строится из последовательностей ДНК для гена, это действительно «генное дерево», показывающее отношения генов, которые могут быть, а могут и не быть такими же, как отношения таксонов. Поскольку считается, что некоторые человеческие гены были получены путем латерального переноса от бактерий, заразивших нас, некоторые гены могут оказаться более тесно связанными с некоторыми бактериями, чем с другими млекопитающими. Если подозревается, что ген возник у эукариот в результате латерального переноса от бактерий, то можно построить дерево, используя последовательности генов как эукариот, так и бактерий. Модель кластеризации должна помочь определить, были ли гены латерально переданы или нет.
4. Мониторинг ограничений на охоту на китов: образцы ДНК из китового мяса, продаваемого в качестве пищи, и от китов в дикой природе были использованы для строительства дерева, указывая не только на виды продаваемых китов, но даже на океан происхождения, что доказали Бейкер и Палумби в 1994 году.
5. Исследование гипотезы происхождения человека «Из Африки»: паттерн кластеризации на дереве, построенном из последовательностей ДНК человека из этнических групп по всему миру, должен помочь указать, как человеческие популяции связаны и, следовательно, как и откуда они распространяются. Этим вопросом занимался Канн, опубликовав результаты в 1987 году, и Гиббонс, – в 1992.
Поскольку последовательности, используемые в большинстве опубликованных исследований, легко доступны через Интернет в базах данных, таких как GenBank, можно самостоятельно исследовать набор данных из этих или других исследований.
Филогенетические методы, основанные на последовательностях, все еще активно исследуются биологами, химиками, статистиками, информатиками, физиками и математиками. Есть много проблем, подходов и методов, которые здесь не затронули. То, как последовательности ДНК идентифицируются как хорошие данные, на которых основывается филогения, как эти последовательности выравниваются и как можно измерить уверенность, которую должны иметь в дереве, – это только три из актуальных тем, которые были проигнорированы. Более полные обзоры классических результатов настоящей тематики можно найти в работах Хиллисеталь 1996 года и Ли 1997 года.
Задачи для самостоятельного решения:
Прежде чем пытаться решить предлагаемые задачи, загрузите базу данных primatedata в MATLAB, чтобы получить доступ к этим аспектам и искажениям, упомянутым выше, все из которых происходят из работы Хаясака от 1988 года. Введите команду who, чтобы увидеть имена переменных, создаваемых данным m-файлом.
5.6.1. Массив расстояний Distprimates представляет собой матрицу 12 × 12, с расстояниями, вычисляемыми по 6-параметрической модели подстановки основания. Названия таксонов в порядке записей матрицы находятся в переменной с именем Namesprimates. Выполните алгоритм присоединения соседей для этих данных с помощью команды nj(Distprimates,Namesprimates{:}).
Нарисуйте метрическое дерево, получившееся в результате.
5.6.2. Используйте имеющиеся знания и свой ответ на предыдущую задачу, чтобы изобразить корневое топологическое дерево, которое могло бы описать эволюционную историю пяти гоминоидов, упомянутых во введении.
5.6.3. Сколько возможных некорневых топологических деревьев может описать эволюцию 12 приматов? Сколько возможных корневых топологических деревьев может описать эволюцию пяти гоминоидов упомянутых во введении к главе?
5.6.4. Команды Nameshominoids=Namesprimates(1:5), Dist hominoids=Dist primates(1:5,1:5) извлекут имена и расстояния между первыми пятью приматами, гоминоидами, упомянутыми во введении к этой главе. Используйте программу nj на данных расстояния только для этих пяти, нарисовав полученное метрическое дерево. Согласуется ли полученная топология с топологией, приведенной в задаче 5.6.1? Согласуется ли метрическая структура? Объясните, как могли возникнуть какие-либо расхождения, которые заметили.
5.6.5. Используйте команду Seqhominoids=Seqprimates([1:5],:) для извлечения последовательностей для гоминоидов. Некоторые последовательности имеют пробелы, обозначаемые символом «–». Сайты, где любая последовательность имеет пробел, который должен быть удален перед вычислением расстояний, нужно предварительно отфильтровать. Команды gaps=(Seq hominoids =='-'), gapsites=find(sum(gaps)), Seq nogaps=Seq hominoids, Seq nogaps(:,gapsites)=[ ] найдут и удалят эти сайты. Используя последовательности без пробелов, вычислите расстояние Джукса-Кантора, 2-параметрическое расстояние Кимуры и логарифмическое расстояние. Напомним, что [DJC, DK2, DLD]=distances(Seqnogaps) сделает это легко.
а. Насколько похожи эти расстояния с расстояниями в массиве Distprimates?
б. Используйте каждый массив расстояний, который создаете, для построения дерева методом присоединения соседей. Все ли они одинаковы с топологической точки зрения? А с метрической?
5.6.6. Исследуйте, насколько разумны модели Джукса-Кантора и Кимуры замещения оснований для описания происхождения гоминоидов от общего предка. Сделайте это, рассматривая две последовательности одновременно, используя compseq.m для вычисления частотного массива оснований в двух последовательностях. Затем вычислите базовые распределения для каждой последовательности и матрицы Маркова, которые описывали бы эволюцию одного в другое. Близки ли они к модели Джукса-Кантора или Кимуры? Выбор другой модели, который делает Хаясака в работе 1988 года, кажется ли необходимым? Объясните почему.
5.6.7. Повторите решение задачи 5.6.5, но используйте все 12 последовательностей приматов. Какое из расстояний, по вашему мнению, наиболее целесообразно использовать? Объясните почему.
5.6.8. Из последовательностей гоминоидов выделите первые 10 информативных сайтов. Используйте их для вычисления оценки экономии (вручную) каждого из деревьев в начале этой главы, а также деревьев с соседними парами (шимпанзе, горилла) и (орангутан, гиббон). Какое из трех является наиболее экономным?
5.6.9. Повторите решение предыдущей задачи, но используя 10 информативных сайтов, выбранных для равномерного распределения между информативными сайтами. Считаете ли, что этот выбор информативных сайтов должен быть более или менее обоснованным, по сравнению с предыдущей задачей? Объясните почему. Очевидно, что использование всех информативных сайтов было бы предпочтительнее, но это невозможно сделать вручную, потому что для этих 5 таксонов их 90.
5.6.10. Если у вас есть доступ к программному обеспечению, которое попытается найти самое экономное дерево, используйте его на полных последовательностях для пяти приматов. Примечание: эти последовательности распространяются вместе с образцом файла данных работы Суоффорда от 2002 года.
5.6.11. Векторные кодирующие сайты и некодирующие сайты содержат индексы кодирующих и некодирующих сайтов в последовательностях приматов. Кодирующие сайты могут быть извлечены с помощью команды Seqcoding=Seqprimates(:,codingsites).
а. Вычислите частотные массивы оснований в кодирующих последовательностях для приматов путем сравнения последовательностей по два за раз. Модель Джукса-Кантора или модель Кимуры кажутся разумными, или думаете, что потребуется другая модель?
б. Повторите часть (а) для некодирующих сайтов последовательностей. Считаете ли, что одна и та же модель может применяться как к кодирующим, так и к некодирующим сайтам? Объясните, ссылаясь на данные.
5.6.12. Поскольку кодирование и некодирование могут быть различными, они могут привести к выводу различных деревьев.
а. Используя только кодирующие участки и логарифмическое расстояние, найдите дерево методом присоединения соседей для 12 приматов. Согласуется ли оно топологически с деревом, сделанным с использованием всех сайтов?
б. Используя только некодирующие участки и логарифмическое расстояние, найдите дерево методом присоединения соседей для 12 приматов. Согласуется ли оно топологически с деревом, сделанным с использованием всех сайтов?
Проектные работы:
1. Передача ВИЧ через зубы
В 1990 году в еженедельном отчете центра по контролю и профилактике заболеваний о заболеваемости и смертности сообщалось, что молодая женщина во Флориде, скорее всего, была инфицирована ВИЧ своим стоматологом. Этот вывод был основан в первую очередь на отсутствии альтернативных объяснений инфекции. Стоматолог, который был ВИЧ-положительным, затем публично попросил, чтобы его пациенты были протестированы. В общей сложности семь пациентов были признаны ВИЧ-положительными.
Конечно, амбулаторные ВИЧ-положительные больные были необязательно инфицированы стоматологом. Можно было бы ожидать, что в большой стоматологической практике будут некоторые инфицированные пациенты, чья инфекция не имеет ничего общего с их стоматологической помощью. Эпидемиологическое расследование попыталось оценить другие факторы риска для пациентов. Вероятно, в то время, как и для других заболевания, не зубные инфекции возникают в качестве сопутствующих. Однако из-за трудностей получения точных ответов от пациентов о поведении высокого риска результаты такого исследования нельзя считать окончательными.
Поскольку никаких других возможных случаев стоматологической инфекции никогда не было зарегистрировано, некоторые сомнения оставались в отношении случаев во Флориде.
В 1992 году в Science появилась статья Оу. Эта работа использовала совершенно другой подход с использованием доказательств ДНК, чтобы попытаться установить вероятность пути стоматологической инфекции для пациентов. Поскольку ВИЧ так быстро мутирует в квазивиды, можно было бы ожидать, что люди, недавно инфицированные непосредственным контактом, имеют более похожие виды, чем те, чей общий источник инфекции был более удален. Поэтому исследователи решили секвенировать очень изменчивый ген оболочки ВИЧ у каждого пациента, стоматолога и некоторых других ВИЧ-инфицированных людей, живущих поблизости, которые, как ожидалось, не имели какого-либо тесного контакта с изучаемыми случаями (то есть с местным контролем). Затем они использовали последовательности для построения филогенетического дерева и по схеме кластеризации определили, какие пациенты, по их мнению, были инфицированы стоматологом.









