Математические модели в естественнонаучном образовании. Том II

Задачи для самостоятельного решения:

5.2.1. Для дерева на рисунке 5.8, построенного методом UPGMA, вычислите таблицу расстояний между таксонами вдоль дерева. Как это соотносится с исходной таблицей данных расстояний?

5.2.2. Предположим, что четыре последовательности

,

,

 и

 ДНК разделены филогенетическими расстояниями, как показано в таблице 5.9. Создайте корневое дерево, показывающее отношения между

,

,

 и

 с помощью UPGMA.

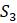
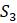
Таблица 5.9.  Данные о расстоянии для задач 5.2.2 и 5.2.5

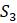
           1.2         .9           1.7

                         1.1         1.9

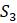
                                        1.6

5.2.3. Выполните UPGMA для данных расстояния в таблице 5.4, которые были использованы в примере FM-алгоритма. Производит ли UPGMA топологически то же дерево, что и алгоритм FM? А метрически?

5.2.4. FM-алгоритм использует тот факт, что данные о расстоянии, относящиеся к трем терминальным таксонам, могут быть точно подогнаны по одному некорневому дереву, относящемуся к ним.

а. Выведите 3-точечных формулы, приведенные в разделе.

б. Если расстояния равны

,

 и

, то каковы длины

,

 и

?

5.2.5. Используйте FM- алгоритм для построения некорневого дерева на данных в таблице 5.9, которая также использовалась в задаче 5.2.2. Насколько отличается получившийся результат?

5.2.6. Предположим, что три терминальных таксона связаны некорневым метрическим деревом.

а. Если три длины ребер равны 0.1, 0.2 и 0.3, объясните, почему гипотеза молекулярных часов должна быть неверной, независимо от того, где находится корень.

б. Если длины трех ребер равны 0.1, 0.1 и 0.2, объясните, почему гипотеза о молекулярных часах может быть верной. В случае, когда гипотеза оказывается верна, где должен находиться корень?

в. Если три длины ребер равны 0.1, 0.2 и 0.2, объясните, почему гипотеза молекулярных часов должна быть неверной, независимо от того, где находится корень.

5.2.7. В то время как данные о расстоянии для 3 терминальных таксонов могут точно соответствовать дереву без корней, при наличии 4 (или более) таксонов это обычно невозможно.

а. Нарисуйте некорневое дерево с терминальными таксонами A, B, C и D. Обозначьте длины пяти ребер

.

б. Используя для расстояния между терминальными таксонами обозначения типа

, запишите уравнения для каждого из 6 таких расстояний выраженных через

. Объясните, почему, если даны числовые значения расстояний между терминальными таксонами, эти уравнения вряд ли будут иметь точное решение.

в. Приведите такой конкретный пример значений 6 расстояний между терминальными таксонами, чтобы уравнения в части (б) не могли иметь точного решения. Приведите еще один пример значений, для которых уравнения могут быть решены.

5.2.8. Известен ряд различных мер для оценки степени согласованности между данными о расстояниях и метрическими деревьями. Пусть

 обозначает расстояние между таксонами

 и

, полученное из экспериментальных данных, а

 обозначает расстояние, полученное при обходе от

 до

 вдоль дерева. Во второй половине прошлого века были предложены следующие три меры:

     (Фитч и Марголиаш, 1967)

         (Фаррис, 1972)

              (Татено и др. , 1982)

Во всех этих мерах суммы включают слагаемые для каждой отдельной пары таксонов

 и

.

а. Вычислите эти меры для дерева, построенного в разделе, используя FM- алгоритм, а также дерева, построенного из тех же данных с помощью UPGMA в задаче 5.2.3. Согласно каждому из этих показателей, какое из двух деревьев лучше подходит для данных?

б. Объясните, почему эти формулы разумно использовать для оценки соответствия. Объясните, как различия между формулами делают их более или менее чувствительными к различным типам ошибок.

Примечание: Фитч и Марголиаш предложили выбрать оптимальное метрическое дерево для соответствия данным как такое, которое минимизирует

. Алгоритм FM был введен в попытке получить аппроксимацию оптимального дерева.

5.2.9. Смоделируйте данные a1, a2, a3 и a4 в соответствии с моделью Джукса-Кантора с молекулярными часами. Сохраните их в файл seqdata.mat путём ввода save seqdata.mat. Загрузите ранее сохраненные данных из файла seqdata.mat в MATLAB путем ввода load seqdata. Затем исследуйте производительность UPGMA с расстоянием Джукса-Кантора, чтобы построить дерево для последовательностей a1, a2, a3 и a4. Все расстояния между последовательностями можно легко вычислить, поместив последовательности в строки массива с помощью команды a=[a1;a2;a3;a4], а затем используя команду [DJC DK2 DLD]=distances(a). Хотя эта команда вычисляет расстояния, используя каждую из формул Джукса-Кантора, 2-параметрической модели Кимуры и формул логарифмического расстояния, для решения этой задачи используйте только расстояния Джукса-Кантора.

а. Нарисуйте дерево UPGMA для 4 таксонов, пометив каждое его ребро длиной.

б. По длинам ребер вычислите расстояния между таксонами при обходе вдоль дерева. Близки ли они к исходным расстояниям?

5.2.10. Повторите решение предыдущей задачи, но используя алгоритм FM вместо UPGMA. Является ли дерево, которое получится в результате, «лучше», чем то, которое получалось раньше? Объясните почему.

5.2.11. Смоделируйте данные b1, b2, b3, b4 и b5 в соответствии с моделью Джукса-Кантора, но без молекулярных часов. Сохраните их в файле seqdata.mat. Исследуйте возможность применения UPGMA с расстоянием Джукса-Кантора для построения дерева для последовательностей b1, b2, b3, b4 и b5 в файле данных seqdata.mat. Полезные команды MATLAB см. в задаче 5.2.9.

а. Нарисуйте дерево UPGMA для 5 таксонов, пометив каждое ребро его длиной.

б. По длинам ребер вычислите расстояния между таксонами вдоль дерева. Близки ли они к исходным данным?

5.2.12. Повторите решение предыдущей задачи, но используя алгоритм FM вместо UPGMA. Является ли дерево, которое получилось в результате, «лучше», чем то, которое было получено ранее? Объясните почему.

5.2.13. Построение дерева с помощью UPGMA предполагает молекулярные часы. Предположим, что некорневое метрическое дерево на рисунке 5.14 правильно описывает эволюцию таксонов A, B, C и D.

Рисунок 5.14.  Дерево для задачи 5.2.13.

а. Объясните, почему, независимо от местоположения корня, молекулярные часы не могли здесь работать.

б. Задайте массив расстояний между каждой парой из четырех таксонов. Выполните UPGMA для этих данных.

в. UPGMA не реконструировала правильное дерево. Что получилось в результате? Что такого было в этом метрическом дереве, что ввело алгоритм в заблуждение?

г. Объясните, почему алгоритм FM также не построит правильное дерево.

5.3. Построение дерева дистанционным методом присоединения соседей

На практике метод UPGMA и FM-алгоритм редко используются для построения дерева, потому что существует дистанционный метод, который как правило работает лучше, чем любой из них. Тем не менее идеи, лежащие в их основе, помогают понять популярный алгоритм присоединения соседей, на котором сосредоточимся в дальнейшем. Чтобы понять, почему UPGMA или FM-алгоритм могут быть ошибочными, рассмотрим метрическое дерево с 4 таксонами на рисунке 5.15. Здесь

 и

 представляют определенные длины, причем

 намного меньше, чем

. Говорим, что вершины

 и

 в этом дереве являются соседями, потому что ребра, ведущие от них, соединяются в общей вершине. Точно так же

 и

 являются соседями, но

 и

 – нет.

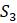
Рисунок 5.15. 4-таксонное метрическое дерево с дальними соседями,

.

Предположим, что метрическое дерево на рисунке 5.15 описывает истинную филогению таксонов. Тогда идеальные данные дадут нам расстояния в таблице 5.10.

Таблица 5.10.  Расстояния между таксонами на рисунке 5.15

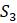
           3х           x+y         2х + y

                         2x+y      x+y

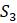
                                         x+2y

Но, если

 намного больше

 (на самом деле,

 уже достаточно хорошо), то ближайшими таксонами по расстоянию являются

 и

, которые не являются соседями. Таким образом, UPGMA или FM-алгоритм, выбирая ближайшие таксоны, выбирает для присоединения не соседей. Самый первый шаг соединения будет неправильным, и как только присоединимся к не соседям, то не восстановим истинное дерево. Суть проблемы заключается в том, что если молекулярные часы не работают, как в случае с деревом на рисунке 5.15, то ближайшие таксоны по расстоянию не обязательно должны быть соседями по дереву.

Вопросы для самопроверки:

– Если

 намного меньше

, то откуда уверенность в том, что молекулярные часы не работают в эволюции, описанной деревом на рисунке 5.15?

Рисунок 5.16. Дерево с соседями

 и

.

Таким образом, выбор ближайших таксонов для присоединения ввел заблуждение; нужен более сложный критерий выбора таксонов для присоединения. Чтобы изобрести его, представьте себе дерево, в котором таксоны

 и

 являются соседями, соединенными в вершине

, а

 каким-то образом соединена с оставшимися таксонами

, как показано на рисунке 5.16.

Если данные точно соответствуют этому метрическому дереву, то для каждого

, дерево будет включать поддерево, подобное изображенному на рисунке 5.17.

Рисунок 5.17. Поддерево дерева на рисунке 5.16.

Но на этом рисунке видим, что

, так как в сумму слева входят только длины четырех ребер, отходящих от листьев дерева, а в сумму справа – все они и, кроме того, удвоенная длина центрального ребра. Это неравенство называется 4-точечным условием для соседей. Если

 и

 являются соседями, то неравенство верно для любых значений

 из диапазона от 3 до

.

Условие 4-точек лежит в основе метода присоединения соседей, но предстоит еще много работы, чтобы перевести его в простую для применения форму. Для фиксированного

 существует

 возможных значения

 удовлетворяющих условию

 при

. Если просуммировать 4-точечные неравенства по этим

, то получим следующее неравенство, содержащее сумму расстояний

.

Чтобы упростить это неравенство, определим общее расстояние от таксона

 до всех других таксонов как

, где расстояние

 в сумме интерпретируется как 0, естественным образом. Затем, добавление

 к каждой стороне исходного неравенства позволяет записать его в более простой форме следующим незамысловатым образом

.

Вычитание

 из частей неравенство придает ему ещё более симметричную форму

.

Наконец, если рассмотреть эту последовательность действий для произвольных

 и

, а не только для

 и

, то можно ввести обозначение

.

Тогда, если

 и

 являются соседями, то имеет место

 для всех

.

Это дает критерий, используемый в методе присоединения соседей: из данных расстояний

, заполоняется новая таблица значений

. Затем для соединения выбирается пара таксонов с наименьшим значением

. Приведенный выше вывод формулы для вычисления

 показывает, что если

 и

 являются соседями, то соответствующее им значение

 будет наименьшим из значений в

-й строке,

-м столбце таблицы. Более глубокий анализ, который провели Штудер и Кеплер в 1988 году, показывает, что если данные идеально подходят к дереву, то наименьшая запись во всей таблице значений

 будет указывать на пару таксонов, которые являются соседями.

Поскольку полный алгоритм присоединения соседей довольно сложен, приведём лишь краткое описание этого метода:

Шаг 1: Учитывая данные о расстоянии для

 таксонов, вычислите новую таблицу значений

. Выберите наименьшее значение, чтобы определить, к каким таксонам присоединиться. Это значение как правило оказывается отрицательным; в этом случае «наименьшее» означает отрицательное число с наибольшим значением по абсолютной величине.

Шаг 2: Если

 и

 должны быть соединены на новой вершине

, временно сверните все остальные таксоны в одну группу

 и определите длины рёбер от

 и

 до

, используя 3-точечные формулы из предыдущего раздела для

,

  и

, как в FM-алгоритме.

Шаг 3: Определите расстояния от каждого из таксонов

 в

 до

, применив 3-точечные формулы к данным расстояния для 3 таксонов

,

 и

. Теперь включите

 в таблицу данных о расстоянии и отбросьте

 и

.

Шаг 4: Таблица расстояний теперь включает

 таксонов. Если есть только 3 таксона, используйте 3-точечные формулы для завершения работы алгоритма. В противном случае вернитесь к шагу 1.

Как уже можете видеть, метод присоединения соседей утомительно реализовывать вручную. Несмотря на то, что шаги относительно просты, легко потеряться в процессе с таким количеством арифметики. В упражнениях найдете пример частично отработанных данных, с которыми нужно завершить алгоритм, для лучшего понимания шагов. После этого предлагается написать и использовать компьютерную программу, чтобы избежать ошибок.

Точность различных методов построения деревьев – трех, описанных до выше в этой главе, и многих других – проверялась в первую очередь путем моделирования мутаций ДНК в соответствии с определенными филогенетическими деревьями, а затем применяя разные методы, сравнивали, как часто они восстанавливают правильное дерево. Некоторые исследования также были проведены с реальными таксонами, связанными известным филогенетическим деревом; деревья, построенные из последовательностей ДНК с использованием различных методов, можно было затем сравнить с заведомо правильным деревом. Эти тесты привели исследователей к большей уверенности в результативности описанного метода присоединения соседей, чем других методах, которые обсуждали ранее. Хотя UPGMA или FM-алгоритм могут быть надежными при некоторых обстоятельствах, метод присоединения соседей хорошо работает с более широким диапазоном данных. Например, если молекулярные часы не существуют, то лучше использовать метод присоединения соседей, поскольку он не предполагает неявных допущений о молекулярных часах. Поскольку в настоящее время накоплено много данных, указывающих на то, что гипотеза молекулярных часов часто нарушается, таким образом метод присоединения соседей становится предпочтительным дистанционным методом для построения дерева.

Задачи для самостоятельного решения:

5.3.1. Перед проработкой примера, в целях более глубокого понимания метода присоединения соседей, полезно вывести формулы используемые на шаге 2 и 3 изложенного алгоритма. Предположим, что решили объединить

 и

 на шаге 1.

а. Покажите, что на шаге 2 расстояния от

 и

 до внутренней вершины

 могут быть найдены по следующим формулам:

,

.