Verification of M.Faraday's hypothesis on the gravitational power lines

central bodies for example, the rotation period of the Sun at the equator is equal to 25 days, and at high latitudes 33 days. It is clear that the inner layers and the entire body as a whole rotate at a higher speed. In accordance with the formula (5) this will lead to a lower constant value C.

The most accurate values are constants C values calculated for solid planets Earth and Mars, the period of rotation of which is determined accurately. The average value of the constants for these two planets is equal 2,48.108 cm/s, which almost coincides with the average value of the constant C = 2,16.108 cm/s, calculated by the formula (3) for satellites "the lunar Prospector", "Smart-1" and "Kaguya".

Thus, with a high degree of reliability can be argued that the constant C in equations (1), (3) and (5) are identical and express the same process gravimagnetic interaction of masses. In the first case the interaction is not rotating Moon and rotating around it satellites, in the second rotating central bodies (the Sun, planets) and their orbital bodies.

The results about gravimagnetism braking when the orbiting bodies driving around a non-rotating Central body – the Moon are in good agreement with the known data that celestial body which does not have its own rotation around its axis (Mercury) or low speed (Venus), do not have satellites. In contrast, satellites of rotating central bodies are braking poorly, especially when moving in orbits with a maximum shear strain of the gravitational field and, accordingly, with a peak concentric orientation of gravimagnetic power lines.

The bulk wave maximum deformation occurs at the equator and extends then in the equatorial plane. Captured satellites quickly decelerate and fall on the Central body. This explains the predominant position of the planets and satellites in the equatorial plane of a rotating central body. Here the greatest shear deformation and concentric orientation gravimagnetic field and the least resistance to movement of the orbital phone. For the same reason it is impossible the existence of polar satellites. Their orbit crosses the force lines at an angle close to 90°. Due to the high gravitational resistance, they quickly decelerate and fall.

A satisfactory explanation also receives the same direction of orbital motion with the rotation of the central bodies and synchronous rotation of the planets and the Sun.

Conclusions

1. The assessment of the gravity-magnetic effect by braking of the satellites of the Moon "Luna-10", "the lunar Prospector", "Smart-1", "Kaguya" and "Chandrayan-1 is given. For the quantitative description of effect used equation gravimagnetic braking similar electrodynamics equation of the Lorentz force and the equation of momentum. The constant part of the equation braking, has a value of C = 2,16.108 cm/s. Estimated time flight of satellites on orbit "the lunar Prospector", "Smart-1" and "Kaguya" is different from the actual ± 14 %.

2. On the basis of gravimagnetism braking orbital bodies is obtained the empirical formula, which expresses the dependence of the orbital planetary and satellite distances from a number of whole (quantum) numbers, mass and period of rotation of the central body. The formula is a constant having the dimension of velocity, equal for the solid planets C = 2,48.108 cm/s. Based on the mapping of constants in braking equation and in the formula of orbital distances the conclusion was made about the identity of these constants.

Литература

1. In Search of Gravitomagnetism, NASA's Gravity Probe B, http://science.nasa.gov/science-news/science-at-nasa/2004/19apr_gravitomagnetism/

2. W. Clifford, Washington University, The Search for Frame-Dragging, http://www.phys.lsu.edu/mog/mog10/node9.html3.

3. J.D. Anderson, Ph.A. Laing, E.L. Lau, A.S. Liu, M.M. Nieto, S.G. Turyshev, Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration, Phys. Rev. Lett. 81, 2858–2861 (1998).

4. Message TASS. A satellite in orbit around the moon. The first scientific results of the flight of the Moon-10, "Pravda", 100 No., 17417, Moscow, April 1966.

5. S. N. Kirpichnikov, Calculation of the motion of artificial satellites of the moon with regard to the radiation pressure of the Sun and Moon, Astronomical journal, so 45, No. 3, S. 675–685 (1968).

6. M. L. Lidov, M. C. Yarskaja, Integrable cases in the problem of the evolution of satellite orbits under the joint influence of the external body and decentralist field of the planet. Space research. 1974. T 12. No. 2. S. 155.

7. «Lunar Prospector»: http://nssdc.gsfc.nasa.gov/planetary/lunarprosp.html

8. «SMART-1»: http://www.esa.int/esaMI/SMART-1/index.html

9. «KAGUYA»: http://www.kaguya.jaxa.jp/index_e.htm

10. «Chandrayaan-1»: http://www.isro.org/chandrayaan/htmls/home.htm

11. A.M. Chechelnitsky, Horizons and new possibilities for astronautical systems megaspectroscopy, Adv. Space Res.,2002, v.29, № 12, p. 1917–1922.

12. F. A. Gareev, Geometric quantization of micro and macro systems. Planetary-wave structure of hadronic resonances, the Message of the joint Institute for nuclear research, Dubna, 1996, S. 296–456.

13. A. So Serkov, Space research,2009, T. 47, No. 4, S. 379.

14. H. Alfvén, H., Arrenius, Evolution of the Solar system, M., Ed. Mir, 1979, S. 14–15.

Chapter 3. The dependence of planetary and satellite distances from the speed rotation of the central bodies

Summary

In Chapter an attempt is made to determine in the equation of planetary and satellite distances the universal constant, which would unite planetary and satellite systems and allow with sufficient accuracy to calculate the elite orbit. To the solution of the problem has been approached through the use of complex representing the square root of the product of the mass of the central body of the system and the period of its rotation.

1. Introduction

The analysis of the dynamic structure of the Solar system, made in the work of B. I. Rabinovich [1], has brought to the fore the problem of stability of periodic motions in systems with commensurate frequencies, which are closely linked to the existence of elite orbits in planetary and satellite systems. A priority issue in this problem is the establishment of the laws of planetary and satellite distances. The author prefers the proposal made earlier by A. M. Chechelnitsky [2], according to which the radii of the elite orbits of planets and satellites Rn determent by quartos law:

Rn = k n2, (1)

where k is a constant and n is an integer number that determines the position of the elite orbit.

The proposed law, in contrast to empirical rules Titius-Bode [3] more accurately describes the dependence of planetary and satellite distances for all systems. In addition, it allows detecting the quantum properties of the gravitational planetary systems.

On this occasion, F. A. Gareev writes [4]: "In the framework of the considered model it is possible to conclude that in the Solar system quanthouse sectorial and orbital velocity and orbital distances of the planets and their satellites". The author on the basis of the equation (1) for planetary and satellite systems received constant (h/mG) is the quantum double sectored speed. The value of this constant for the different systems is presented in table 1. According to the author's constant satisfactorily within ±5 % remains constant for the same system. However, between the difference reaches 5 decimal orders of magnitude.

Table 1. The values of the constants (a/mG) for planetary and satellite systems and its relationship with the rotation parameters of the Central bodies systems.

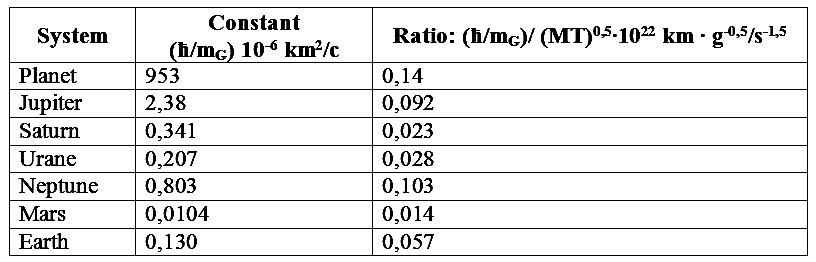
This article in the framework of representations arising from law formulated in equation (1), an attempt is made to establish a universal constant, which would unite planetary and satellite systems. When this work has taken into account the statement of Alven H. [5], "the emergence of an ordered system of secondary bodies around the primary body – whether it be the Sun or a planet, definitely depends on two parameters initial body: its mass and speed".

2. Orbital distance for satellite systems

To establish the relationship between constant k and rotation parameters of the central bodies of planetary and satellite systems were calculated constants for planetary systems, and systems of Jupiter, Saturn, Uranus and Neptune. Table 2 shows the calculated values of k, for the planetary system, calculated by equation (1). The values of n for the calculation were taken from the work of F A. Gareev. The obtained average value of the constants k= 6,28∙1011 cm with standard deviation of 0.49∙1011 cm. Also the dependence of planetary distances from the squares of integers represented in Fig. 1, which confirms the correctness of the values of the integer n.

Fig.1. The dependence of the orbital distances rn in the planetary system from squares of integers n

Table 2. The values of the constant k in equation (1) for the planetary system.

Similar calculations were done for the satellite systems of Jupiter, Saturn, Uranus and Neptune. In table 3 and Fig.2 shows the data for the satellite systems of Jupiter. The system has 63 satellites. Many rely on close orbits and were therefore combined into groups. For example, in orbits with an average distance 23813∙108 cm turns 28 satellites. All of them are given one quantum number 29.

In the system of Jupiter are 32 elite orbits, which are comparable with the planetary system, where they are 30. The constancy of the constants k observed satisfactorily for all orbits except the first two quantum numbers 2 and 3. The average value of the constants k = 28,6∙108 cm with standard deviation of 0.3∙108 cm excluding the first two orbits, deviations from which are outside the statistical sample. The dependence of the orbital distances in the satellite system of Jupiter is given also in Fig.2.

Graph expressing this dependence was used to determine the values of the quantum numbers n. All experimental points, expressing the satellite or group of satellites with the same orbital distances satisfactorily fit to a straight line, as required by equation (1). Each orbital distance on the ordinate corresponds to the value of n2

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.