Бесконечная сила. Как математический анализ раскрывает тайны вселенной

Если метафора со стеной кажется вам слишком мрачной и негуманной (кому захочется вечно приближаться к недосягаемой стене?), рассмотрите такую аналогию: все, что движется к какому-то пределу, подобно герою, занятому бесконечным поиском. Это не бесполезное занятие, как бессмысленная задача Сизифа, обреченного вечно вкатывать камень на гору только для того, чтобы увидеть, как он снова скатывается вниз. Когда в математике происходит приближение к пределу (как наши фигуры с выступами приближались к предельному прямоугольнику), это подобно тому, как главный герой стремится к чему-то, что, как он знает, невозможно, но все же надеется на успех, воодушевляясь прогрессом в своих попытках достичь недостижимой звезды.

Притча о 0,333…

Чтобы подкрепить важные идеи, что в бесконечности все упрощается и что пределы подобны недостижимым целям, возьмем пример из арифметики. Это задача преобразования обыкновенной дроби – например, 1/3 – в десятичную (в нашем случае 1/3 = 0,333…). Я хорошо помню, как моя школьная учительница математики мисс Стэнтон учила нас это делать. Запомнилось это потому, что она внезапно заговорила о бесконечности.

До этого момента я никогда не слышал, чтобы взрослые говорили о бесконечности. Мои родители определенно этого не делали. Это казалось секретом, о котором знали только дети. На детской площадке о нем постоянно упоминали в насмешках и издевках:

– Ну ты и дурак!

– А ты дурак вдвойне!

– А ты дурак бесконечность раз!

– А ты дурак бесконечность раз плюс один!

– Это то же самое, что бесконечность, идиот!

Такие поучительные разговоры убедили меня в том, что бесконечность ведет себя не так, как обычное число. Она не становится больше, если к ней прибавить 1. Даже добавление бесконечности не поможет. Несокрушимые свойства делали ее окончательным аргументом в дворовых разборках. Побеждает тот, кто применит бесконечность первым.

Однако никто из учителей до мисс Стэнтон не упоминал о бесконечности. Все в нашем классе уже знали о конечных десятичных дробях, используемых для представления денежных сумм, например 10,28 доллара, где есть две цифры после запятой. Напротив, бесконечные десятичные дроби, где после запятой было бесконечно много чисел, казались странными на первый взгляд, но становились естественными, как только мы начали изучать обыкновенные дроби.

Мы узнали, что дробь 1/3 можно записать как 0,333…, где многоточие означало, что тройки повторяются до бесконечности. Это имело для меня смысл, потому что, пытаясь поделить 1 на 3 в столбик, я застрял в бесконечном цикле: 1 меньше 3, поэтому получаем в частном ноль целых, дописываем к единице 0, делим 10 на 3, получаем 3 и остаток 1; в итоге нужно снова делить 1 на 3, то есть мы возвращаемся к тому, с чего начали. Выхода из цикла не было, а значит, тройки при делении будут повторяться: 0,333…

Многоточие после 0,333 истолковывается двумя способами. Наивное толкование состоит в том, что существует буквально бесконечное количество троек, находящихся справа от десятичной запятой вплотную друг к другу. Конечно, мы не можем записать их все, раз их бесконечно много, но с помощью многоточия показываем, что они там есть, по крайней мере в нашей голове. Я назову такую интерпретацию актуальной бесконечностью Преимущество ее в том, что она выглядит простой и здравой, пока мы не желаем особо задумываться о том, что означает бесконечность.

Более изящное толкование состоит в том, что 0,333… представляет собой некоторый предел – в точности такой же, как предельный прямоугольник для наших фигур в доказательстве с пиццей или стена для незадачливого путешественника. Только здесь 0,333… отображает предел последовательных десятичных чисел, которые мы генерируем при делении 1 на 3. Чем больше этапов в процессе деления, тем больше троек в десятичном разложении 1/3. Мы можем получить сколь угодно хорошее приближение к 1/3. Если нам не нравится 1/3 ≈ 0,3, мы можем сделать еще шаг и получить 1/3 ≈ 0,33 и так далее. Я назову это толкование потенциальной бесконечностью Она «потенциальна» в том смысле, что приближения можно получать сколь угодно долго. Ничто не мешает сделать миллион, миллиард или любое иное количество шагов. Преимущество этого толкования в том, что нам незачем прибегать к такому туманному понятию, как бесконечность. Мы всегда можем оставаться в области конечного.

Для работы с равенством вида 1/3 = 0,333… не имеет значения, какой точки зрения мы придерживаемся. Они одинаково состоятельны и дают одни и те же математические результаты в любых нужных нам вычислениях. Однако в математике существуют ситуации, когда понятие актуальной бесконечности может вызвать логический хаос. Именно это я подразумевал, когда писал во введении о големе бесконечности. Иногда действительно важно, как мы думаем о результатах процесса, приближающегося к какому-то пределу. Делая вид, что процесс в реальности заканчивается и каким-то образом достигает нирваны бесконечности, подчас можно попасть в неприятную ситуацию.

Притча о многоугольнике с бесконечным числом углов

В качестве примера возьмем круг, расставим на его границе (окружности) через равные промежутки определенное количество точек и соединим их отрезками. При трех точках получим равносторонний треугольник, при четырех – квадрат, при пяти – правильный пятиугольник и так далее, последовательно получая все новые правильные многоугольники.

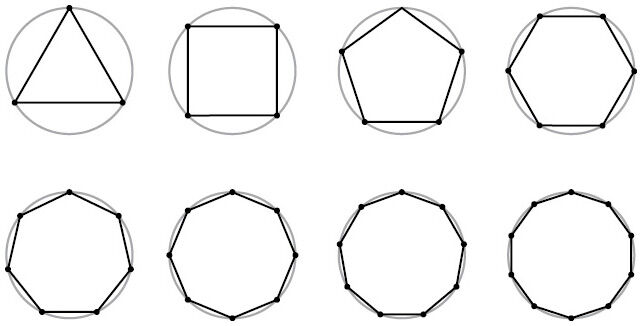
Обратите внимание, что чем больше точек мы используем, тем ближе наш многоугольник к кругу. При этом стороны многоугольников становятся все короче и многочисленнее. Наш круг – предел для построенных многоугольников.

Таким образом, бесконечность снова соединяет два мира. На этот раз она ведет нас от прямолинейности к криволинейности, от угловатых фигур к гладкому кругу, тогда как в случае с пиццей бесконечность, наоборот, преобразовала круг в прямоугольник.

Конечно же, на любом шаге многоугольник по-прежнему остается многоугольником. Это еще не круг и никогда им не станет. Фигуры приближаются к кругу, но никогда не совпадут с ним. Здесь мы имеем дело с потенциальной бесконечностью, а не с актуальной. Так что с логической точки зрения все безукоризненно.

Но что, если бы мы могли пройти весь путь до актуальной бесконечности? Был бы итоговый многоугольник с бесконечным количеством углов и бесконечно короткими сторонами кругом? Заманчиво так думать, ведь тогда многоугольник окажется гладким. Все углы будут сошлифованы. Все станет идеальным и красивым.

Очарование и опасность бесконечности

Здесь заложен общий принцип: пределы часто проще, чем приближения, ведущие к ним. Круг проще и изящнее, чем любой из угловатых многоугольников, к нему приближающих. То же самое относится и к доказательству с помощью пиццы, где предельный прямоугольник проще и элегантнее, нежели бугристые фигуры с некрасивыми выступами, и к дроби 1/3. Это проще и приятнее, нежели любое из неуклюжих приближений с большими числителями и знаменателями вроде 3/10, 33/100 или 333/1000. Во всех этих случаях предельная фигура или число проще и симметричнее, чем конечные приближения.

В этом и состоит очарование бесконечности. Здесь все становится лучше.

Помня об этом, давайте вернемся к притче о многоугольнике с бесконечно большим количеством углов. Нужно ли сделать решительный шаг и сказать, что круг – это действительно многоугольник с бесконечно большим количеством бесконечно малых сторон? Нет. Мы не должны поддаваться искушению и так поступать, поскольку это означает впасть в грех актуальной бесконечности. Это обрекло бы нас на логический ад.

Чтобы понять, почему, предположим, что мы на миг подумали, будто круг – на самом деле многоугольник с бесконечным числом углов и бесконечно малыми сторонами. Какова длина этих сторон? Если она равна 0, то общая длина всех сторон – бесконечность, умноженная на 0, – должна давать длину окружности. Но представьте окружность вдвое большего размера. Точно так же ее длина должна равняться бесконечности, умноженной на 0. Получается, бесконечность, умноженная на 0, должна равняться и длине нашей окружности, и вдвое большему числу. Что за ерунда? Не существует разумного способа определить результат умножения бесконечности на ноль, а потому нет разумного способа рассматривать круг как правильный многоугольник с бесконечным числом сторон.

Тем не менее в таком интуитивном представлении есть нечто искушающее. Подобно библейскому первородному греху, по той же причине трудно сопротивляться и первородному греху анализа – соблазну считать, что круг – это правильный многоугольник с бесконечным числом сторон. Он соблазняет нас запретным знанием, идеями, недоступными для обычных средств. На протяжении тысячелетий геометры пытались вычислить длину окружности. Если бы круг можно было заменить многоугольником со множеством крохотных прямых сторон, задача была бы гораздо проще.

Прислушиваясь к шипению этого змея-искусителя – но все же сдерживаясь, используя потенциальную бесконечность вместо более заманчивой актуальной, – математики научились решать задачу о длине окружности и другие загадки кривых. В следующих главах мы узнаем, как им это удалось, а пока попробуем еще глубже понять, насколько опасной может быть актуальная бесконечность. Этот грех ведет ко многим другим, включая тот, о котором учителя предупреждали нас в первую очередь.

Грех деления на ноль

Во всем мире школьников учат, что делить на ноль нельзя. Должно быть, они шокированы существованием такого табу. Предполагается, что числа дисциплинированны и хорошо себя ведут. Урок математики – место для логики и рассуждений. И все же можно задавать о числах простые вопросы, на которые нет ответов, или пытаться сделать с ними простые вещи, которые не работают или не имеют смысла. Деление на ноль – одна из них.

Корень проблемы – в бесконечности. Деление на ноль вызывает бесконечность примерно так же, как доска для спиритических сеансов – духов из другого мира. Это рискованно. Не ходите туда.

Тем, кто не в силах сопротивляться искушению и желает понять, почему в тенях скрывается бесконечность, советуем поделить 6 на какое-нибудь маленькое число, близкое к нулю, но не равное ему, например 0,1. В этом ничего запретного нет. Если разделить 6 на 0,1, получится 60, довольно прилично. Поделим 6 на еще меньшее число, скажем 0,01; ответ будет больше – 600. Если мы отважимся разделить 6 на число, которое гораздо ближе к 0, допустим, на 0,0000001, то ответ будет еще больше и составит 60 000 000. Тенденция ясна. Чем меньше знаменатель, тем больше частное. В пределе, когда знаменатель приближается к нулю, частное стремится к бесконечности. Вот настоящая причина, почему нельзя делить на 0. Малодушные говорят, что ответ неопределенный, но на самом деле он бесконечный.

Все это можно представить себе следующим образом. Вообразите, что вы делите 6-сантиметровую линию на части длиной 0,1 сантиметра. Получается 60 кусков, уложенных вплотную друг к другу.

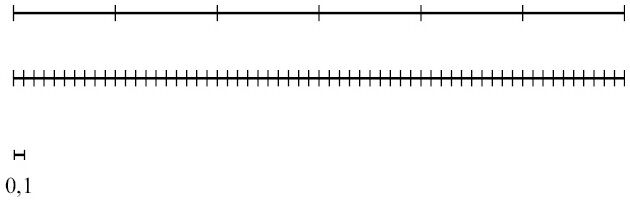
Точно так же (но я не буду пробовать это нарисовать) эту линию можно поделить на 600 частей по 0,01 сантиметра или на 60 000 000 частей по 0,0000001 сантиметра.

Если мы продолжим и доведем это безумное деление до предела, то придем к заключению, что наша 6-сантиметровая линия состоит из бесконечного числа частей нулевой длины. Возможно, это звучит правдоподобно. В конце концов, линия состоит из бесконечного количества точек, и каждая точка имеет нулевую длину.

Но с философской точки зрения нервирует то, что аналогичное рассуждение можно применить к линии любой длины. В самом деле, в числе 6 нет ничего особенного. Мы могли бы с равным успехом утверждать, что линия длиной 3 сантиметра, или 49,57, или 2 000 000 000 состоит из бесконечного числа точек нулевой длины. Очевидно, что умножение 0 на бесконечность может дать нам любой мыслимый результат – 6, 3, 49,57 или 2 000 000 000. С математической точки зрения это ужасно.

Грех актуальной бесконечности

Прегрешение, которое втянуло нас в эту путаницу, заключалось в том, что мы вообразили, будто действительно можем достичь предела и трактовать бесконечность как достижимое число. Еще в IV веке до нашей эры греческий философ Аристотель[30] предупреждал, что такое обращение с бесконечностью способно привести к различным логическим неприятностям. Он выступал против актуальной бесконечности[31], уверяя, что смысл имеет только потенциальная бесконечность.

В контексте разрезания линии на части потенциальная бесконечность означает, что линию можно разрезать на сколь угодно большое количество частей, но оно всегда конечно, а длина частей не равна 0. Это вполне допустимо и не вызывает никаких логических затруднений.

Что запрещено – так это идея, что можно пройти весь путь до актуальной бесконечности и получить бесконечное число частей нулевой длины. Аристотель считал, что это ведет к бессмыслице – как в нашем случае, когда произведение бесконечности и 0 может дать любое число. Поэтому он запретил пользоваться актуальной бесконечностью в математике и философии. Математики поддерживали его мнение в течение следующих двадцати двух столетий.

Когда-то в далекие доисторические времена кто-то понял, что числа никогда не заканчиваются. Вместе с этой мыслью родилась бесконечность. Это числовой аналог глубин, скрытых в нашей психике, в наших ночных кошмарах о бездонных ямах и в наших надеждах на вечную жизнь. Именно бесконечность лежит в основе множества наших мечтаний, страхов и безответных вопросов. Насколько велика Вселенная? Сколько длится вечность? Насколько могуществен Бог? Тысячи лет бесконечность сбивает с толку лучшие умы человечества во всех областях мысли – от религии и философии до науки и математики. Ее запрещали, объявляли вне закона и отвергали. Во времена инквизиции монах Джордано Бруно[32] был сожжен заживо на костре за предположение, что Бог в своей бесконечной силе создал бесчисленные миры.

Парадоксы Зенона

Примерно за два тысячелетия до казни Джордано Бруно бесконечность осмелился созерцать другой отважный философ. Зенон Элейский (около 490–430 до нашей эры) изложил ряд апорий (парадоксов), связанных с пространством, временем и движением, и бесконечность играла в них главную роль. Эти апории предвосхитили идеи, положенные в основу анализа, и обсуждаются до сих пор. Бертран Рассел называл их неизмеримо тонкими и глубокими[33].

Мы не знаем, что именно пытался показать своими рассуждениями Зенон, поскольку ни одно из его сочинений не сохранилось, если они вообще существовали. Его рассуждения дошли до нас в передаче Платона и Аристотеля, которые в основном пытались их опровергнуть. В их пересказе Зенон пытался доказать, что изменения невозможны. Наши чувства говорят нам иное, но они нас обманывают. Изменение, согласно Зенону, – это иллюзия.

Особенно известны три парадокса Зенона[34],[35]. Первый, «Дихотомия», аналогичен загадке стены, но гораздо печальнее. Он гласит, что вам не удастся даже сдвинуться с места, поскольку для того, чтобы сделать первый шаг, нужно сделать полшага, а перед этим – четверть шага и так далее. Так что вы не только не сможете добраться до стены, но даже не сможете начать движение.

Это блестящий парадокс. Кто бы мог подумать, что для шага требуется выполнить бесконечно много подзадач? Хуже того, нет самой первой задачи, которую надо выполнить. Она не может состоять в том, что нужно сделать полшага, потому что до этого пришлось бы сделать четверть шага, а до того – восьмую часть шага и так далее. Если вы думаете, что у вас много дел перед завтраком, представьте, что вам нужно закончить бесконечное количество дел, прежде чем добраться до кухни.

Другой парадокс, названный «Ахиллес и черепаха», утверждает, что быстрый бегун (Ахиллес) никогда не догонит медленного бегуна (черепаху), если у того будет фора.

К тому времени, когда Ахиллес достигнет места, откуда отправилась в путь черепаха, она успеет немного продвинуться вперед. К тому моменту, когда Ахиллес достигнет этого нового места, черепаха снова продвинется, и так далее. Поскольку все мы считаем, что быстрый бегун может обогнать медленного, то либо наши чувства нас обманывают, либо что-то не так с нашими рассуждениями о движении, пространстве и времени.

В этих первых двух парадоксах Зенон, похоже, возражал против принципиальной непрерывности пространства и времени, то есть против того, что их можно делить до бесконечности. Его умной стратегией было применение доказательства от противного (некоторые утверждают, что он его и изобрел), известное среди юристов и логиков как reductio ad absurdum (доведение до абсурда). В обоих парадоксах Зенон предположил непрерывность пространства и времени, а затем вывел из этого допущения противоречие, поэтому предположение о непрерывности должно быть ложным. Анализ основан именно на этом предположении, а потому ставки тут весьма высоки. Он опровергает Зенона, демонстрируя ошибки в его рассуждениях.

Например, вот как анализ справляется с Ахиллесом и черепахой. Допустим, что черепаха стартует в 10 метрах перед Ахиллесом, а Ахиллес бежит вдесятеро быстрее своей соперницы – скажем, 10 метров в секунду против 1 метра в секунду. Таким образом, за 1 секунду Ахиллес отыгрывает 10-метровую фору черепахи. За это время черепаха продвинется на 1 метр. Чтобы покрыть это расстояние, Ахиллесу понадобится еще 0,1 секунды. За это время черепаха преодолеет еще 0,1 метра. Продолжая рассуждать в том же духе, мы видим, что последовательные отрезки времени, которые нужны Ахиллесу, чтобы покрыть разделяющее расстояние, складываются в бесконечный ряд:

1 + 0,1 + 0,01 + 0,001 + … = 1,111… секунд.

Если записать это число в виде обыкновенной дроби, получим 10/9 секунды. Именно столько времени понадобится быстроногому герою мифа, чтобы догнать черепаху. И хотя Зенон был прав в том, что Ахиллесу требуется выполнить бесконечное количество задач, в этом нет ничего парадоксального. Как показывает математика, он может справиться с ними за конечный промежуток времени.

Такое рассуждение использует анализ. Мы просто суммируем бесконечный ряд и вычисляем предельное значение, как делали при обсуждении, почему 0,333… = 1/3. Всякий раз, когда мы работаем с бесконечной записью десятичных чисел, мы применяем анализ (хотя большинство людей отнеслись бы к этому как к школьной арифметике).

Кстати, анализ – не единственный способ справиться с такой задачей. Мы могли бы использовать алгебру. Для этого нам нужно выяснить, где в произвольный момент времени t находится на трассе каждый из соперников. Пусть Ахиллес начинает в нулевой точке. Поскольку он бежит со скоростью 10 метров в секунду, а расстояние равно произведению скорости на время, то в момент t он пробежит 10 × t. Что касается черепахи, то она начинает двигаться в точке 10 и перемещается со скоростью 1 метр в секунду, поэтому в момент t она находится в точке 10 + 1 × t. Чтобы определить время, когда герой настигнет соперницу, нужно приравнять эти два выражения, поскольку с алгебраической точки зрения это означает, что Ахиллес и черепаха находятся в одной точке в один момент времени. Получаем уравнение

10t = 10 + t.

Чтобы решить его, вычитаем t из обеих частей и получаем 9t = 10. Делим обе части на 9 и получаем t = 10 / 9 секунды, то есть ровно тот же ответ, что нам дал анализ. Таким образом, с точки зрения анализа в ситуации с Ахиллесом и черепахой нет никакого парадокса. Если пространство и время непрерывны, все прекрасно работает.

Зенон в цифровом мире

В третьей апории под названием «Стрела» Зенон выступает против альтернативной идеи, что пространство и время дискретны[36]

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

В оригинале используется слово calculus, у которого в русском языке нет однозначного соответствия. В английском языке это слово применяется как для математического анализа или для анализа бесконечно малых в целом, так и для наименования различных областей высшей математики, для которых мы используем слова «анализ» (например, vector calculus – векторный анализ) или «исчисление» (например, differential calculus – дифференциальное исчисление). В данной книге под термином «анализ» будет подразумеваться анализ бесконечно малых, который объединяет интегральное и дифференциальное исчисление. Прим. пер.

2

Калтех – Калифорнийский технологический институт. Частный университет в Калифорнии, один из лучших в США. Прим. пер.

3

Wouk, The Language God Talks, 5.

4

Альтернативное мнение можно найти в книгах: Barrow and Tipler, Anthropic Cosmological Principle; Rees, Just Six Numbers; Davies, The Goldilocks Enigma; Livio, Is God a Mathematician?; Tegmark, Our Mathematical Universe; и Carroll, The Big Picture. С философскими аспектами анализа можно познакомиться в Simon Friederich, Fine-Tuning, Stanford Encyclopedia of Philosophy, https://plato.stanford.edu/entries/fine-tuning/.

5

Adams, Hitchhiker’s Guide, и Gill, Douglas Adams’ Amazingly Accurate Answer.

6

В юмористическом фантастическом романе Адамса «Автостопом по галактике» (издана на русском языке: Адамс Д. Автостопом по галактике. М.: АСТ, 2002) специальный суперкомпьютер «Думатель» находит «ответ на главный вопрос жизни, Вселенной и всего такого», и это оказывается 42. Прим. пер.

7

Wouk, The Language God Talks, 6.

8

Герман Воук скончался в мае 2019 года в возрасте 103 лет. Прим. пер.

9

Исторические аспекты проблемы представлены в книгах: Boyer, The History of the Calculus, и Grattan-Guinness, From the Calculus. Dunham, The Calculus Gallery; Edwards, The Historical Development; и Simmons, Calculus Gems, которые рассказывают историю анализа на примере некоторых наиболее красивых задач и их решений.

10

Stewart, In Pursuit of the Unknown; Higham et al., The Princeton Companion; и Goriely, Applied Mathematics, передают дух, широту и практичность прикладной математики.

11

Kline, Mathematics in Western Culture, и Newman, The World of Mathematics, соединяют математику с более широкой культурой. Я провел много времени в старших классах, читая эти два шедевра.

12

О математике и физике смотрите Maxwell, On Physical Lines of Force, и Purcell, Electricity and Magnetism. О понятиях и истории смотрите Kline, Mathematics in Western Culture, 304–21; Schaffer, The Laird of Physics; и Stewart, In Pursuit of the Unknown, глава 11. Биографию Максвелла и Фарадея смотрите в книге: Forbes and Mahon, Faraday, Maxwell.

13

Stewart, In Pursuit of the Unknown, глава 8.

14

В оригинале Truth in, truth out – каламбурная отсылка к фразе Wine in, truth out, что примерно соответствует нашей пословице «что у трезвого на уме, то у пьяного на языке». Прим. пер.

15

Einstein, Physics and Reality, 51. Этот афоризм часто передают так: «Самая непостижимая вещь во Вселенной – то, что она постижима». Другие примеры цитат Эйнштейна, подлинных или приписываемых ему, смотрите в книгах: Calaprice, The Ultimate Quotable Einstein, и Robinson, Einstein Said That.

16

Wigner, The Unreasonable Effectiveness; Hamming, The Unreasonable Effectiveness; и Livio, Is God a Mathematician? См. https://coollib.net/b/322251/

17

Перевод Ю. А. Данилова. Прим. пер.

18

Asimov, Asimov’s Biographical Encyclopedia, 4–5; Burkert, Lore and Science; Guthrie, Pythagorean Sourcebook; и C. Huffman, Pythagoras, https://plato.stanford.edu/archives/sum2014/entries/pythagoras/. Martínez в книгах Cult of Pythagoras и Science Secrets развенчивает многие мифы о пифагорейцах с осторожностью и уничижительным юмором.