
Полная версия
It All Adds Up
Let us now return to our Geode. Theaetetus’ proof is final: it is impossible for a polyhedron with several hundred faces to be perfectly regular. But then what do you do when you are an architect and you want to create a building that resembles a regular sphere as closely as possible? It is technically difficult to design the building in a single piece. No, there’s nothing you can do about that, and you have to assemble a multitude of small faces. But how do you create such a structure?
We can imagine various solutions. One of these involves taking one of the Platonic solids and modifying it. Consider the icosahedron, for example. With its twenty triangular faces, it seems the roundest of the five. To smooth it out, each of its faces can be subdivided into several smaller faces. The polyhedron obtained in this way can then be deformed, as though one were inflating it by blowing into it, in order to come closer to a sphere.
Here, for example, is what happens when you subdivide each face of the icosahedron into four smaller triangles.
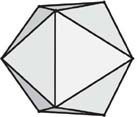
The icosahedron

Inflated icosahedron with subdivided faces

Icosahedron with faces subdivided into four
In geometry, such a polyhedron is called a geode. Etymologically, this means a figure that is shaped like the Earth – that is to say, it resembles a sphere. There is nothing very complicated about this principle. It is precisely this construction that was used for the Geode of la Villette! The subdivision of the faces is, however, very much finer: the basic triangles of the icosahedron are here subdivided into 400 smaller triangles, making a total of eight thousand triangular facets.
In reality, the Geode has rather fewer than 8,000 facets – only 6,433 – since it is not complete. Its base, which rests on the ground, is truncated and some triangles are missing. Nevertheless, this structure allows us to explain the presence of the twelve irregularities. The latter correspond simply to the twelve vertices of the basic icosahedron. In other words, these are the points where the original large triangles met in fives to form the points of the icosahedron. These vertices, which were originally pointed, have been flattened with the increase in the number of faces to the point of becoming almost invisible. However, their presence remains firmly fixed in the layout of the triangles, and the twelve irregularities are there to remind attentive passers-by of this.
Theaetetus probably didn’t imagine that his studies would one day permit the construction of buildings such as the Geode. And the great power of mathematics, as in the kind that the scholars of ancient Greece developed, lies in its formidable ability to engender new ideas. The Greeks gradually began to detach their questioning from concrete problems and thus to generate original and inspiring models out of simple intellectual curiosity. Although they might often have seemed to have no concrete use at the time they were conceived, these models sometimes turned out to be astonishingly useful long after their creators had disappeared.
Nowadays, we come across the five Platonic solids in different contexts. For example, they are well suited for use as dice in board games. Their regularity ensures that the dice are balanced, that is to say that all the faces have the same chance of occurring. Everyone is familiar with cubic dice with six faces, but the most inveterate players know that numerous other games also use the other four shapes to vary the enjoyment and the probabilities.
As I move away from the Geode, a little further on I come across some children who have produced a ball and are starting a makeshift game of football on the lawns of la Villette. They are not aware of it, but at this moment they too owe a very great deal to Theaetetus. Have they noticed that their ball also has its geometric patterns? Most footballs are formed on the same model: twenty hexagonal pieces (six-sided) and twelve pentagonal pieces (five-sided). On traditional balls, the hexagons are white while the pentagons are black. And even when the surface of the ball carries all kinds of printed inscriptions, you only have to look carefully at the seams between the different pieces to see once again the inevitable twenty hexagons and twelve pentagons.
A truncated icosahedron – that is the name geometers give to the football. And its structure is owed to the same constraints as the Geode: it has to be as regular and as round as possible. The only thing is that, in order to achieve this result, the creators of this model used a different method. Instead of subdividing the faces in order to be able to round off the corners, they simply chose to cut off the corners. Imagine an icosahedron in modelling clay, take a knife and simply slice off the vertices. The twenty triangles with their points sliced off become hexagons, while the twelve points removed lead to the appearance of the twelve pentagons.

The twelve pentagons on a football thus have the same origin as the twelve irregularities on the surface of the Geode: they are the original locations of the twelve vertices of the icosahedron.
As I leave the Parc de la Villette, I come across a girl with a handkerchief. What is wrong? I wonder. She doesn’t seem to be doing too well. Perhaps she has fallen victim to a nasty attack of micro-icosahedra? Certain microscopic organisms such as viruses naturally assume the form of icosahedra or dodecahedra. This is the case with the rhinoviruses, which are responsible for most colds.
If these tiny creatures adopt such forms, it is for the same reasons for which we use these forms in architecture or for our footballs, namely for the sake of symmetry and economy. Thanks to icosahedra, balls consist of only two different types of pieces. In the same way, the virus membrane consists only of a few different types of molecules (four for the rhinoviruses) that fit together by always repeating the same pattern. The genetic code needed to create such an envelope is thus very much more concise and economical than what it would have taken to describe a structure with no repeatable symmetry at all.
Once again, Theaetetus would have been very surprised to learn of all the applications in which his polyhedra are hidden.
Time to leave the Parc de la Villette and pick up the chronological flow of our history again. How did ancient mathematicians such as Theaetetus come to raise ever more general and theoretical questions? To understand this, we must go back several thousand years to the eastern rim of the Mediterranean.
While the Babylonian and Egyptian cultures were slowly declining, ancient Greece was about to enter its greatest centuries. From the sixth century BC onwards, the Greek world entered an unprecedented period of cultural and scientific effervescence. Philosophy, poetry, sculpture, architecture, theatre, medicine and even history were also disciplines that underwent a true revolution. To this day the exceptional vitality of that period retains a certain fascination and mystery, and last but not least in that vast intellectual movement, mathematics had pride of place.
When we think of ancient Greece, the first image that springs to mind is often that of the city of Athens, dominated by its Acropolis. There, we imagine citizens in white robes, who had just invented the first democracy in history, strolling among Pentelic marble temples and a few olive trees. But this vision comes nowhere near to a representation of the whole of the Greek world in all its diversity.
In the eighth and seventh centuries BC, a swarm of Greek colonies spread around the edges of the Mediterranean. Sometimes there was an integration between these colonies and the local peoples, with a partial adoption of the latter’s customs and lifestyles. It is far from the case that all Greeks shared the same form of existence. Their food, pleasures, beliefs and political systems varied widely from one region to another.
Thus, Greek mathematics did not emerge in a specific place where all the scholars knew each other and met each other daily, but over a vast geographic and cultural region. The driving forces behind the mathematical revolution included the contact with the older civilizations whose heir it became, and the mix of Greece’s own diversity. Numerous scholars undertook a pilgrimage to Egypt or the Middle East at some stage in their lives, as an obligatory rite of passage in their training. A sizeable amount of Babylonian and Egyptian mathematics was integrated and extended by Greek scholars.
The first great Greek mathematician, Thales, was born at the end of the seventh century in the town of Miletus (present-day Milet), on the south-west coast of what is now Turkey. Although he is mentioned in various sources, it is difficult today to extract reliable information about his life and his work. As with many scholars of this period, various legends spread by overzealous disciples grew up after his death, and have made it hard to unravel the true from the false. The scholars of that time were not averse to spinning yarns, and they not infrequently came to an accommodation with the truth when it did not suit them.
According to one of the many stories put about on the subject, Thales was particularly absent-minded: he is said to have been a prime example from an age-old tradition of scatter-brained scholars. One tale reports that one night he was seen to fall into a well while roaming with his nose in the air observing the stars. Another tells us that he died aged almost eighty while attending a sporting event: so wrapped up did he become in the spectacle that he forgot to eat and drink.
His scientific prowess is also the subject of singular tales. Thales is viewed as the first person to have correctly predicted a solar eclipse. This one took place in the middle of a battle between the Medes and the Lydians, on the banks of the Halys River in the west of what is now Turkey. When night intervened in broad daylight, the warriors saw it as a message from the gods, and decided at once to make peace. Nowadays, the prediction of eclipses or their reconstitution in the past has become child’s play for our astronomers. Thanks to them, we know that this eclipse took place on 28 May 584 BC, making the battle of Halys the oldest historical event that we are able to date with such accuracy.
Thales’ greatest success was achieved on a journey to Egypt. The story goes that the Pharaoh Amasis in person challenged him to measure the height of the Great Pyramid. Until then, the Egyptian scholars who had been consulted had failed to answer the question correctly. Thales not only met the challenge, but did so in an elegant way, using a particularly clever method. He planted a stick vertically in the ground and waited for the time of day when the length of its shadow was equal to its height. At that very same moment, he marked and then measured the shadow of the pyramid, which likewise must be equal to its height. That did the trick!
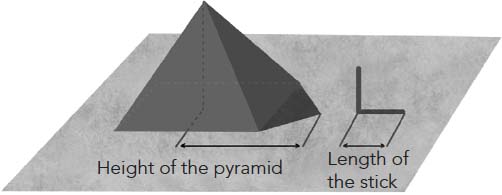
The story is certainly entertaining, but once again its historical truth is dubious. Moreover, as it is told, the anecdote is quite scornful of the Egyptian scholars of the period, although papyruses such as that copied by Ahmes show that these scholars knew perfectly well how to calculate the height of their pyramids more than a thousand years before Thales came on the scene. So where does the truth lie? Did Thales really measure the height of the pyramid? Was he the first to use the shadow method? And what if he had simply measured the height of an olive tree in front of his house in Miletus, and his disciples took it upon themselves to embroider the story after his death? We have to abide by the evidence, and we shall probably never have it.
Be that as it may, Thales’ geometry, on the other hand, is very real, and whether he applied it to the Great Pyramid or to an olive tree, the shadow method is no less appealing. This method represents a particular case of a property now known as Thales’ theorem. Several other mathematical results are also attributed to Thales: the circle is divided in two equal parts by any diameter (fig. 1); the angles at the base of an isosceles triangle are equal (fig. 2); the opposite angles produced at the point of intersection of two straight lines are equal (fig. 3); if the three vertices of a triangle lie on a circle and one side passes through the centre of this circle, then the triangle is a right-angled triangle (fig. 4). In fact, this last statement is sometimes also referred to as Thales’ theorem.
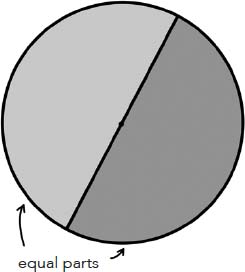
Fig. 1
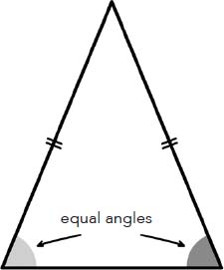
Fig. 2
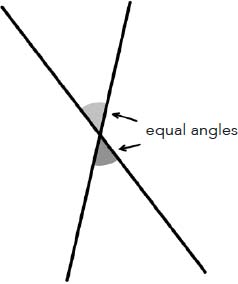
Fig. 3
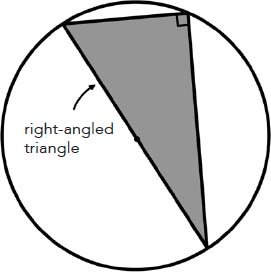
Fig. 4
I want to look at this strange word that is as fascinating as it is awesome: what is a theorem? Etymologically, the word comes from the Greek thea (contemplation) and horáō (to see), so a theorem would be a sort of observation on the world of mathematics, a fact that would have been noted, examined and then recorded by mathematicians. Theorems can be transmitted orally or in writing, and are similar to one’s grandmother’s recipes or to weather lore that has been tested over the generations and is confidently believed to be true. One swallow does not make a summer, bay leaves soothe rheumatism, and the 3-4-5 triangle has a right angle. These are things we believe to be true and that we keep in mind in order to use them when they are relevant.
According to this definition, the Mesopotamians, the Egyptians and the Chinese also stated theorems. However, beginning with Thales, the Greeks gave them a new dimension. For them, a theorem not only had to state a mathematical truth, but that truth must be formulated in the most general way possible, and accompanied by a proof of its validity.
Back to one of the properties attributed to Thales: that the diameter of a circle divides the circle into two equal parts. Such an assertion may seem disappointing coming from a scholar of Thales’ calibre. It seems self-evident; why did we have to wait until the sixth century BC for such a trivial assertion to be stated? There is no doubt that Egyptian and Babylonian scholars must have known that a long time beforehand.
Make no mistake. The audacious thing about that property attributed to Thales is not so much its content as its formulation. Thales dared to speak about a circle without saying precisely which one. In order to state the same rule, the Babylonians, Egyptians and Chinese would have used an example. Draw a circle of radius 3 and draw one of its diameters, they would have said, and this circle is divided into two equal parts by this diameter. And when one example did not suffice for an understanding of the rule, they would have given a second one, a third, and a fourth if necessary. They would have given as many examples as needed to enable readers to understand that they could repeat the same procedure on every circle they might meet. But the general assertion was never formulated.
Thales reached a milestone.
‘Take a circle, any one you like, I don’t need to know which. It may be enormous or tiny. Draw it in the horizontal, in the vertical or on an inclined plane, it doesn’t matter to me. I don’t care at all about your particular circle and how you have drawn it. However, I assert that its diameter divides it into two equal parts.’
With this operation, Thales definitively assigned the status of abstract mathematical objects to geometric figures. This step in thinking was similar to that taken 2,000 years earlier by the Mesopotamians when they considered numbers independently from the objects counted. A circle was no longer a figure drawn on the ground, on a tablet or on a papyrus. The circle became a fiction, an idea, an abstract ideal all of whose real representations are merely imperfect instances.
From that point on, mathematical truths were stated in a concise and general manner, independently of the various particular cases they covered. It is these statements that the Greeks then called theorems.
Thales had several disciples in Miletus. The two most famous were Anaximenes and Anaximander. Anaximander in turn had his own disciples, who included a certain Pythagoras, who would give his name to the most famous theorem of all time.
Pythagoras was born at the start of the sixth century BC on the island of Samos, situated off the coast of what is now Turkey, and less than 40 kilometres away from the town of Miletus. As a young man he gained experience through his travels in the ancient world, and chose to settle in the town of Croton, in the south-east of present-day Italy. It was there that he founded his school in 532 BC.
Pythagoras and his disciples were not just mathematicians and scholars, but also philosophers, monks and politicians. Yet it must be said that if we were to transpose it to our time, the community begun by Pythagoras would undoubtedly be perceived to be among the most obscure and most dangerous of sects. The life of the Pythagoreans was governed by a set of precise rules. For example, anyone wishing to join the school had to go through a period of five years of silence. The Pythagoreans had no individual possessions: all their belongings were shared. They used various symbols such as the tetractys or the pentagram in the shape of a star with five branches to recognize one another. Moreover, the Pythagoreans thought of themselves as enlightened people, and thought it normal that political power should come to them. They firmly repressed the rebellions of towns that refused to accept their authority. In fact, it was in one such riot that Pythagoras died at the age of eighty-five.
The number of myths of all kinds that were invented around Pythagoras is also impressive. His disciples were scarcely lacking in imagination, as we can now see. According to them, Pythagoras was the son of the god Apollo. The name Pythagoras also means literally ‘he who was announced by the Oracle’: the Oracle of Delphi was in fact the oracle of the temple of Apollo, and it is she who is said to have told Pythagoras’ parents about the forthcoming birth of their child. According to the Oracle, Pythagoras would be the most handsome and wisest of men. After such a birth, the Greek scholar was predestined for great things. Pythagoras remembered all his previous lives. According to this, he had in particular been one of the heroes of the Trojan War called Euphorbus. In his youth, Pythagoras took part in the Olympic Games and took the laurels in all the pygmachia events (pugilism, the ancestor of our boxing). Pythagoras invented the very first musical scales. Pythagoras was able to walk in the air. Pythagoras died and was resuscitated. Pythagoras was a talented soothsayer and healer. Pythagoras had control over animals. Pythagoras had a golden thigh.
While most of these legends are so far-fetched that no one believes them, in other cases the jury is still out. Is it true, for example, that Pythagoras was the first to use the word ‘mathematics’? The facts are so sketchy that some historians have even come to speculate that Pythagoras was a purely fictional person, dreamed up by the Pythagoreans to serve as their tutelary figure.
Therefore, since it is not possible to learn more about the man, let us return to the subject for which he is still known to schoolchildren the whole world over more than 2,500 years after his death: Pythagoras’ theorem. What does this famous theorem tell us? Its statement may seem astonishing, because it establishes a link between two apparently unconnected mathematical concepts: right-angled triangles and the square numbers.
Let us return to our favourite triangle, the 3-4-5. From the lengths of the three sides we can construct three square numbers: 9, 16 and 25.

We now spot a curious coincidence: 9 + 16 = 25. The sum of the squares of sides 3 and 4 is equal to the square of side 5. This might be put down to chance, yet if we try to reproduce this calculation for a different right-angled triangle, it still works. Consider, for example, the triangle 65-72-97, which appears on the Babylonian Plimpton tablet. The three corresponding squares are 4,225, 5,184 and 9,409. And Pythagoras’ theorem does not fail: 4,225 + 5,184 = 9,409. For such large numbers, it becomes difficult to believe in a simple coincidence.
You can try with all the right-angled triangles you like, small or large, fat or thin, it always works. In a right-angled triangle, the sum of the squares of the two sides that form the right angle is always equal to the square of the third side (which we call the hypotenuse). And it also works the other way round: if, in a given triangle, the sum of the squares of the two smallest sides is equal to the square of the largest side, then the triangle is right-angled. That is Pythagoras’ Theorem.
Of course, we do not know for certain whether Pythagoras or his disciples actually contributed to this theorem. Even though the Babylonians never expressed it in the general form that we have just seen, it is highly likely that they already knew this result more than one thousand years earlier. For otherwise, how would they have been able to discover all the right-angled triangles that appear on the Plimpton tablet with such accuracy? The Egyptians and the Chinese probably also knew the theorem, which was also clearly stated in the commentaries that were added to the Nine Chapters in the centuries after it was written.
Some accounts claim that Pythagoras was the first to give a proof of the theorem. However, there is no reliable source to confirm this, and the oldest proof that has come down to us is only the one in Euclid’s Elements, which was written three centuries later.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.


