
Полная версия
It All Adds Up
In one room, a loutrophoros with red figures takes my breath away. A loutrophoros is a tall slender vase with two handles; its function is to carry water for bathing – this one is almost one metre tall. The friezes come thick and fast, and I begin by ticking them off by category. One. Two. Three. Four. Five. In a few seconds I have identified five of the seven geometric structures. The vase is standing against the wall, but when I lean over I can see that it has a frieze of the sixth category on its hidden face. I’m missing just one frieze now. That would be too much to ask. Surprisingly, the missing one is not the same one as the day before. Times have changed, and fashions too; I’m no longer missing the glide symmetry, but the combination comprising vertical symmetry, rotation and glide symmetry.
I am looking frantically for it, my eyes scanning each and every feature of the object. But I can’t find it. I’m slightly disappointed and preparing to give up when my gaze alights on a detail. In the middle of the vase there is a depiction of a scene involving two people. At first sight, there does not seem to be a frieze at that point. Then, an object at the bottom right-hand corner of the scene stops me in my tracks: a vase on which the central person is resting. A vase drawn on the vase! This technique of mise en abyme, in which an image contains a smaller copy of itself, makes me smile. I look closer. The image is a little damaged, but there is no doubt about it: this image of a vase itself contains a frieze and, what a miracle, it’s the one that I’m missing!
Despite my repeated efforts I will fail to find another piece with the same property. This loutrophoros seems to be unique in the Louvre’s collections: it is the only one that bears all seven categories of friezes.
A little further on, another surprise awaits me: friezes in 3D! And I had thought perspective was an invention of the Renaissance. Bright and dark areas skilfully positioned by the artist create a chiaroscuro effect, adding volume to the geometric shapes that pursue each other around the circumference of this gigantic receptacle.
The further I proceed, the more questions arise. Some pieces are not covered by friezes but by tilings. In other words, the geometric patterns no longer simply fill a narrow band running around the object, but now also invade its whole surface, thereby reducing the possibilities for geometric combinations.
After the Greeks come the Egyptians, the Etruscans and the Romans. I discover illusions of filigree lace carved in stone. The stone threads are interwoven and pass alternately above and below one another in a perfectly regular meshing. Then, as if the works of art are not sufficient in themselves, I am soon surprised to find myself observing the Louvre itself, its ceilings, its tiled floors and its door surrounds. As I return home, it’s as though I am unable to stop myself. In the street, I look at the balconies of buildings, the patterns on the clothes worn by passers-by, the walls in the corridors of the Métro, etc.
You have only to change how you look at the world to see mathematics emerge. The search is fascinating. It has no end.
And the adventure is just beginning.
2
AND THEN THERE WERE NUMBERS
In those days, in Mesopotamia, the region was thriving. At the end of the fourth millennium BC, the small villages we visited earlier had transformed into flourishing towns. Some of them now already had several tens of thousands of inhabitants. Technology was advancing at a rate never before seen. Artisans, whether they were architects, goldsmiths, potters, weavers, carpenters or sculptors, needed to exhibit constant ingenuity to cope with the technical challenges they confronted. Metallurgy was not yet at its peak, but it was a work in progress.
Gradually, a network of routes came to criss-cross the whole region. Cultural and commercial exchanges multiplied. Increasingly complex hierarchies established themselves and Homo sapiens discovered the joys of administration. All this took extensive organization. To establish some degree of order, it was high time for our species to invent writing and enter history. Mathematics was to play a cutting-edge role in this nascent revolution.
Following the course of the Euphrates, we leave the northern plateaux that saw the birth of the first sedentary villages, and head towards the Sumer region that covers the plains of Lower Mesopotamia. It is here, in the southern steppes, that the chief population centres were then concentrated. Along the river we reach the towns of Kish, Nippur and Shuruppak. These towns were still young, but the centuries that lay ahead of them had grandeur and prosperity in store.
Then, suddenly, Uruk emerges.
The town of Uruk was a human anthill, which lit up the whole of the Near East with its prestige and power. It was built mainly of mud bricks, and its orangey hues extended over more than one hundred hectares, so that the new visitor could stray for hours in its crowded streets. At the heart of the town, several monumental temples had been constructed, dedicated to An, the father of all the gods, and above all to Inanna, the Lady of the Heavens. It was for her that the Eanna Temple was built, its largest building 80 metres long by 30 metres wide, and hugely impressive to the many travellers who were drawn here.
Summer was coming, and as in every year at this time, the whole town was beginning to bustle with a particular activity. Soon the flocks of sheep would leave for the northern pasturelands, returning only at the end of the hot season. For several months, it would be the job of the shepherds to manage their animals, to keep them fed and watered, and to return them safe and sound to their owners. The Eanna Temple itself owned several flocks, the largest numbering several tens of thousands of animals. The convoys were so impressive that some were escorted by soldiers to protect them from the dangers of the journey. However, for the owners it was out of the question to let their sheep go without a few precautions. As for the shepherds, the contract was clear: as many animals must return as had set out. There was no margin for losing part of the herd or for clandestine trading.
This then led to a problem: how do you compare the size of the flock that leaves with the size of the one that returns?
In response to this, a system of clay tokens had already been developed several centuries earlier. There were several types of token, each representing one or more objects or animals according to its shape and the patterns traced on it. For a sheep, there was a simple disc marked with a cross. At the time of leaving, a number of tokens corresponding to the size of the flock were placed in a receptacle. On return, the owners had only to compare the flock with the contents of the receptacle to check that no animal was missing. Much later on, these tokens were given the Latin name of calculi, ‘small stones’, from which the term calculus was derived.
This method was practical, but it had a disadvantage. Who looked after the tokens? For suspicion cuts both ways, and the shepherds were in turn worried that unscrupulous owners might add extra tokens to the urn during their absence. Then they could claim compensation for non-existent sheep.
After much racking of brains, a solution was found. The tokens were to be kept securely in a sealed hollow clay sphere or envelope. At the time it was sealed, both parties were to leave their signatures on the surface of the sphere to certify its authenticity. It was then impossible to modify the number of tokens without breaking the sphere. The shepherds could leave without worrying.
But then, once again, it was the owners who found drawbacks in this method. For their business requirements, they needed to know the number of animals in their flocks at any time. How could this be achieved? Could the number of sheep be committed to memory? This was not straightforward, since the Sumerian language did not yet have words to denote such large numbers. Could you have an unsealed duplicate of all the tokens contained in all the envelopes? This was not very practical.
At last a solution was found. A reed stem was cut and used to trace out on the surface of each sphere a representation of the tokens it contained. That made it possible to reference the contents of the envelope at will without having to break open the sphere.
This method now seemed to suit everyone. It was widely used, not only to count sheep, but also to set a seal on all kinds of agreements. Cereals such as barley or wheat, wool and textiles, metal, jewels, precious stones, oil and pottery also had their tokens. Even taxes were controlled by tokens. In short, at the end of the fifth millennium, in Uruk, any contract in due and proper form had to be sealed by a hollow-sphere envelope with its clay tokens.
All this worked wonderfully well, but then one day a new idea emerged, so brilliant and so simple that one wonders why no one had thought of it before. Since the number of animals was inscribed on the surface of the sphere, what was the point of continuing to put the tokens inside it? And what was the point of continuing to make spheres? You could simply draw a representation of the tokens on an arbitrary piece of clay – for example, on a flat tablet.
This came to be called writing.
I’m back in the Louvre. The collections of the department of Near Eastern Antiquities bear witness to this story. The first thing that strikes me when I see these sphere–envelopes is their size. These clay spheres that the Sumerians created simply by turning them around their thumbs are scarcely any larger than ping-pong balls. As for the tokens, they are no bigger than a centimetre.
Stepping further into the museum brings us to the first tablets. Their numbers grow and they quickly come to fill whole display slots. Over time, the writing became more precise and took on its cuneiform appearance, comprising small notched wedges in the shape of a nail, with a stem and a head. Following the disappearance of the first Mesopotamian civilizations at the beginning of the modern era, most of these pieces had lain quietly for centuries beneath the ruins of those deserted towns before they were unearthed by European archaeologists from the seventeenth century onwards. They were only gradually deciphered during the nineteenth century.
These tablets are not very large either. Some of them are the size of simple visiting cards, but covered with hundreds of tiny signs which are crammed together one above the other. Mesopotamian scribes did not waste the slightest portion of the clay when they wrote. The museum’s explanation cards placed alongside these pieces enable me to interpret these mysterious symbols. They concern livestock, jewels or cereals.
Next to me, some tourists are taking photos with their tablets – this is an amusing nod to the carousel of history where writing appears on so many different media, from clay to paper, by way of marble, wax, papyrus and parchment, and which, in a final jest, has endowed electronic tablets with the shape of their earthenware ancestors. The face-to-face encounter of these two objects has something particularly touching about it. For all we know, in five thousand years’ time these two tablets may find themselves next to each other again, but on the same side of the glass.
Time has passed. We are now at the start of the third millennium BC, and another step has been taken: numbers have been freed from the objects that they count. Previously, in the case of sphere–envelopes and the very first tablets, the counting symbols depended on the objects in question. A sheep is not a cow, so the symbol for counting a sheep was not the same as the one for counting a cow. Every object that could be counted had its own symbols, just as it had had its own tokens.
But all that was over and done. Numbers had acquired their own symbols. In other words, eight sheep were no longer counted using eight symbols each denoting a sheep, but instead the figure eight was written down followed by the symbol for a sheep. And to count eight cows, you simply had to replace the symbol for a sheep by that for a cow. The number itself stayed the same.
This stage in the history of thought was absolutely fundamental. If I had to assign an actual date to the birth of mathematics, I would be sure to choose this moment: the moment when numbers came into existence in their own right, when numbers became detached from reality to observe it from a greater height. Everything before that had simply amounted to a gestation period. Bifaces, friezes, tokens – all these amount to preludes in the scheme that led towards the birth of numbers.
From that point on, numbers became an abstract concept, and that is what gave mathematics its identity: it is the science of abstraction par excellence. The objects that mathematics studies do not have a physical existence. They are not material, they are not made of atoms, they’re purely ideas. And yet these ideas are remarkably effective when it comes to making sense of the world.
It is undoubtedly no accident that the need to be able to write down numbers acted at the time as a determining factor in the emergence of writing. While other ideas could be transmitted orally without any problem, it seemed on the other hand difficult to establish a system of numbers without moving to a written notation.
Can we, even today, dissociate the idea we have of numbers from our written representation of them? If I ask you to think of a sheep, how do you see it? You probably represent it as a bleating animal with four legs and a woolly back. You would never think of visualizing the five letters of the word ‘sheep’. Yet if I talk now about the number one hundred and twenty-eight, what do you see? Do the 1, the 2 and the 8 take shape in your brain and come together as though they are written in the intangible ink of your thoughts? Our mental representation of large numbers appears to be definitively linked to their written form.
This example came out of the blue. Although for everything else, writing was just a means of transcribing something that had previously existed in the spoken language, now, in the case of numbers, it was the writing that would dictate the language. Think about it: when you pronounce ‘One hundred and twenty-eight’, you are just reading 128: 100 + 20 + 8. Above a certain threshold, it becomes impossible to speak about numbers without the written medium. Before they were written down, there were no words for large numbers.
To this day, some indigenous peoples still only have a very limited number of words for designating numbers. For example, the members of the Pirahã tribe of hunter-gatherers who live on the banks of the Maici River in Amazonia only count to two. Above that, they use a single word signifying ‘several’ or ‘many’. Again in Amazonia, the Munduruku only have words for up to five – that is to say a hand.
In our modern societies, numbers have invaded our everyday lives. They have become so omnipresent and indispensable that we often forget just how brilliant the idea is, and that it took our ancestors centuries to provide us with evidence of this.
Throughout the ages, very many procedures for recording numbers have been invented. The simplest of these involves writing down as many signs as the desired number – for example, a sequence of bars side by side. We often still use this method, for example to count the points in a game.

The oldest known indication of the probable use of this procedure dates back to well before the invention of writing by the Sumerians. The so-called Ishango bone (actually two baboon bones) was found in the 1950s on the shores of Lake Edward in what is now the Democratic Republic of Congo and dates back some twenty thousand years. The bones are 10 and 14 centimetres long, and feature a large number of more or less regularly spaced incisions. What was the role of these incisions? It is likely that this was a first counting system. Some people think the bones are a calendar, while others extrapolate an already highly advanced knowledge of arithmetic. It is hard to know for sure. The two bones are now on display in the museum of the Royal Belgian Institute of National Sciences in Brussels.

This method of counting using a mark for each unit added rapidly reached its limits as soon as there was a need to manipulate relatively large numbers. Packets were introduced to achieve a greater speed.
The Mesopotamian tokens could already represent several units. For example, there was a particular token for representing ten sheep. This principle was retained at the time that writing came in. There are symbols to denote packets of 10, of 60, of 600, of 3,600 and of 36,000.

Here we also see the search for a logic in the construction of the symbols. For example, the 60 and the 3,600 are multiplied by 10 when a circle is included inside them. With the arrival of cuneiform writing, these first symbols were gradually transformed into the following:

Because it was so close to Mesopotamia, Egypt did not lag far behind in adopting writing, and developed its own numeration symbols from the start of the third millennium.
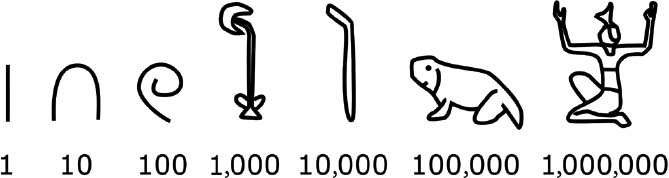
The system was then purely decimal: each symbol had a value ten times greater than the one before.
These additive systems, in which one just has to add the values of the written symbols, became very popular throughout the world, and numerous variants were unveiled throughout antiquity and also much of the Middle Ages. They were used, in particular, by the Greeks and the Romans, who simply employed the letters of their respective alphabets as numerical symbols.
Alongside the additive systems, a new form of notation for numbers gradually emerged: numeration by position. In these systems, the value of a symbol was defined to depend on the position it occupies within the number. Once again, the Mesopotamians were the first to come up with this.
In the second millennium BC, it was the town of Babylon that now shone brightly over the Near East. Cuneiform writing was still in vogue, but now, just two symbols were used: the simple nail that had the value ‘1’ and the chevron with the value ‘10’.
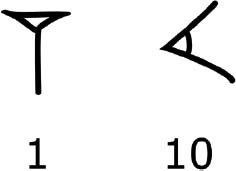
These two signs were used to provide an additive notation for all numbers up to 59. For example, the number 32 was written as three chevrons followed by two nails.

Then, from 60 onwards, groups were introduced, where the same symbols were used to denote groups of 60. Thus, in the same way as in our present-day notation, where the figures read from right to left denote the units, then the tens, then the hundreds, in this Babylonian numeration the units are read first, then the sixties, then the three-thousand-six-hundreds (that is, sixty sixties), and so on, where each rank has a value sixty times greater than its predecessor.
For example, the number 145 consists of two sixties (which make 120) to which you have to add 25 units. The Babylonians would therefore have denoted it as follows:
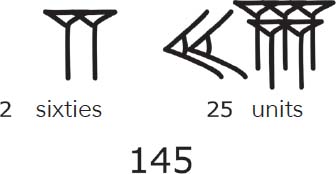
Based on this system, Babylonian scholars developed an extraordinary knowledge. They had a good understanding of the four basic operations of addition, subtraction, multiplication and division, and also of square roots, powers and reciprocals. They produced extremely detailed arithmetic tables and developed very good solution techniques for equations that they set themselves.
However, all this was soon forgotten. The Babylonian civilization was in decline, and a large part of its mathematical advances would be consigned to oblivion. There would be no more numeration by position and no more equations. Indeed, there was a time lag of centuries before these questions became the flavour of the day again, and it was only in the nineteenth century that the decoding of cuneiform tablets reminded us that the Mesopotamians had tackled these things before everyone else.
Following the Babylonians, the Mayans also devised a positional system, in this case with base 20. Then it was the turn of the Indians to invent a system with base 10. This last system was used by Arab scholars before it reached Europe at the end of the Middle Ages. Its symbols became known as Arabic figures, and soon spread all over the world.
0 1 2 3 4 5 6 7 8 9
With numbers, mankind gradually came to understand that it had just invented a tool for describing, analysing and understanding the world around it that surpassed any purpose it might have hoped for.
Sometimes we have been so pleased with numbers that we have even overdone it. The birth of numbers represented at the same time the birth of the practice of various forms of numerology. This involves attributing magical properties to numbers, interpreting them beyond the bounds of reason, and attempting to read into them messages from the gods and about the fate of the world.
In the sixth century BC, the Greek scholar Pythagoras made numbers the fundamental concept of his philosophy when he declared: ‘Everything is a number.’ According to him, it is numbers that produce geometric figures, which in turn give rise to the four elements of matter – fire, water, earth and air – of which all living things are made. Pythagoras thus created a whole system around numbers. The odd numbers were associated with the masculine, while the even numbers were feminine. The number 10, represented as a triangle called the tetractys, became a symbol of harmony and of the perfection of the cosmos. Pythagoreans were also behind the origin of arithmancy, which claimed to read people’s characters by associating numerical values with the letters comprising their names.
In parallel, there began to be discussions about what constitutes a number. Some authors believed that the unit – 1 – is not a number, because a number denotes a plurality and so can only be considered from 2 onwards. It was even asserted that in order for it to be able to generate all the other numbers, 1 must be simultaneously even and odd.
Later, increasingly animated discussions developed concerning the zero, the negative numbers and the imaginary numbers. In each case, the admission of these new ideas to the circle of numbers led to debate and forced mathematicians to broaden their ideas.
In short, numbers have never ceased to raise questions, and human beings still need time to learn to master these strange creatures that are their brainchildren.
3
LET NO ONE IGNORANT OF GEOMETRY ENTER
Once numbers had been invented, it did not take long for the discipline of mathematics to spread its wings. Various core branches such as arithmetic, logic and algebra gradually sprouted within it, developed to maturity and asserted themselves as disciplines in their own right.




