
Полная версия
The Music of the Primes: Why an unsolved problem in mathematics matters
Humboldt’s drive from teaching science as a practical tool to the more aesthetic notion of knowledge for its own sake had filtered down to Schmalfuss’s classroom. The teacher steered Riemann’s reading away from mathematical texts full of formulas and rules that were aimed at feeding the demands of a growing industrial world, and guided him towards the classics of Euclid, Archimedes and Apollonius. With their geometry, the ancient Greeks sought to understand the abstract structure of points and lines, and they were not hung up on the particular formulas behind the geometry. When Schmalfuss did give Riemann a more modern text, Descartes’s treatise on analytical geometry – a subject rife with equations and formulas – the teacher could see that the mechanical method developed in the book did not appeal to Riemann’s growing taste for conceptual mathematics. As Schmalfuss later recalled in a letter to a friend, ‘already at that time he was a mathematician next to whose wealth a teacher felt poor’.
One of the books that was sitting on Schmalfuss’s shelf was a contemporary volume the teacher had acquired from France. Published in 1808, Théorie des Nombres by Adrien-Marie Legendre was the first text to record the observation that there seemed to be a strange connection between the function that counted the number of prime numbers and the logarithm function. This connection, discovered by Gauss and Legendre, was only based on experimental evidence. It was far from clear whether, as one counted higher, the number of primes would always be approximated by Gauss’s or Legendre’s function.
Despite the volume’s 859 large quarto pages, Riemann gobbled it up, returning the book to his teacher just six days later with the precocious declaration, ‘This is a wonderful book; I know it by heart.’ His teacher could not believe it, but when he examined Riemann on its contents during his final examinations two years later, the student answered perfectly. That marked the beginning of the career of one of the giants of modern mathematics. Thanks to Legendre, a seed was sown in the young Riemann’s mind that in later life was to blossom in spectacular fashion.
His final examinations over, Riemann was eager to join one of the vigorous new universities that were driving the educational revolution in Germany. His father, though, had other ideas. Riemann’s family was poor, and his father hoped that Bernhard would join him in the Church. The life of a clergyman would provide him with a regular income with which he could support his sisters. The only university in the Kingdom of Hanover to offer theology was not one of these new establishments but the University of Göttingen, founded over a century before, in 1734. So in 1846, to comply with his father’s wishes, Riemann made his way to the dank town of Göttingen.
Göttingen sits quietly in the gentle hills of Lower Saxony. At its heart lies a small medieval town enclosed by ancient ramparts. This is the Göttingen that Riemann would have known, and it still retains much of its original character. The streets wind narrowly between half-timbered houses topped with red-tiled roofs. The Brothers Grimm wrote many of their fairy tales in Göttingen, and one can imagine Hansel and Gretel running through its streets. In the centre stands the medieval town hall, whose walls display the motto ‘Away from Göttingen there is no life.’ For those at the university that was certainly the feeling. The academic life was one of self-sufficiency. Although theology had predominated in the early years of the university, the winds of academic change sweeping across Germany had stimulated Göttingen’s scientific curriculum. By the time Gauss was appointed as professor of astronomy and director of the observatory in 1807, it was science rather than theology for which Göttingen was becoming famous.
The fire for mathematics that the teacher Schmalfuss had ignited in the young Riemann was still burning strong. His father’s wish that he study theology had brought him to Göttingen, but it was the influence of the great Gauss and Göttingen’s scientific tradition that left its mark during that first year. It was only a matter of time before Greek and Latin lectures gave way to the temptation of courses in physics and mathematics. With trepidation, Riemann wrote to his father suggesting that he would like to switch from theology to mathematics. His father’s approval meant everything to Riemann. With a sense of relief he received his father’s blessing, and immediately immersed himself in the scientific life of the university.
To a young man of such talent, Göttingen soon began to feel small. Within a year Riemann had exhausted the resources available to him. Gauss, by now an old man, had become quite withdrawn from the intellectual life of the university – since 1828 he had spent only one night away from the observatory, where he lived. At the university he only lectured on astronomy, and in particular on the method that had made him famous when he’d rediscovered the ‘lost’ planet Ceres many years before. Riemann had to look elsewhere for the stimulus he needed to take the next step in his development. He could see Berlin was where the buzz of intellectual activity was the loudest.
The University of Berlin had been greatly influenced by the successful French research institutes, such as the École Polytechnique, that had been founded by Napoleon. It had, after all, been founded during the French occupation. One of the key mathematical ambassadors was a brilliant mathematician by the name of Peter Gustav Lejeune-Dirichlet. Although he was born in Germany in 1805, Dirichlet’s family was of French origin. A return to his roots took him to Paris in 1822, where he spent five years soaking up the intellectual activity that was bubbling out of the academies. Wilhelm von Humboldt’s brother Alexander, an amateur scientist, met Dirichlet on his travels and was so impressed that he secured him a position back in Germany. Dirichlet was something of a rebel. Perhaps the atmosphere on the streets in Paris had given him a taste for challenging authority. In Berlin, he was quite happy to ignore some of the antiquated traditions demanded by the rather stuffy university authorities, and often flouted their demands to demonstrate his command of the Latin language.
Göttingen and Berlin offered emerging scientists such as Riemann contrasting academic climates. Göttingen revelled in its independence and isolation. Few seminars were presented by anyone from beyond the city walls. It was self-sufficient and generated great science from the fuel burning within. Berlin, on the other hand, thrived on the stimulation coming from outside Germany. The ideas feeding through from France mixed with the forward-looking German approach to natural philosophy to create a heady new cocktail.
The different climates of Göttingen and Berlin suited different mathematicians. Some would never have succeeded without contact with new ideas from external sources. The success of other mathematicians can be traced back to an isolation which forced them to find an inner strength and new languages and modes of thought. Riemann would turn out to be someone whose breakthroughs came from contact with the wealth of new ideas that were in the air, and he could see that Berlin was the place to be.
Riemann made his move in 1847 and remained in Berlin for two years. While there, he was able to get his hands on papers by Gauss which he had not been able to prise from the reticent master in Göttingen. He attended lectures by Dirichlet, who was later to play a part in Riemann’s dramatic discoveries about prime numbers. By all accounts, Dirichlet was an inspiring lecturer. One mathematician who attended his lectures put it thus:
Dirichlet cannot be surpassed for richness of material and clear insight … he sits at the high desk facing us, puts his spectacles up on his forehead, leans his head on both hands, and … inside his hands he sees an imaginary calculation and reads it out to us – that we understand it as well as if we too saw it. I like that kind of lecturing.
Riemann made friends with several young researchers in Dirichlet’s seminars who were equally fired up by their passion for mathematics.
Other forces were also bubbling away in Berlin. The revolution of 1848 that swept away the French monarchy spread from the streets of Paris throughout much of Europe. It found its way to the streets of Berlin while Riemann was studying there. According to accounts of his contemporaries, it had a profound impact on him. On one of the few occasions in his life on which he joined with those around him on anything other than an intellectual level, he enlisted in the student corps defending the king in his Berlin palace. It is reputed that he did a continuous sixteen-hour stint on the barricades.
Riemann’s response to the mathematical revolution spreading from the Paris academies was not that of a reactionary. Berlin was importing not only political propaganda from Paris, but also many of the prestigious journals and publications coming out of the academies. Riemann received the latest volumes of the influential French journal Comptes Rendus and holed himself up in his room to pore over papers by the mathematical revolutionary Augustin-Louis Cauchy.
Cauchy was a child of the Revolution, born a few weeks after the fall of the Bastille in 1789. Undernourished by the little food available during those years, the feeble young Cauchy preferred to exercise his mind rather than his body. In time-honoured fashion, the mathematical world provided a refuge for him. A mathematical friend of Cauchy’s father, Lagrange, recognised the young boy’s precocious talent and commented to a contemporary, ‘You see that little young man? Well! He will supplant all of us in so far as we are mathematicians.’ But he had interesting advice for Cauchy’s father. ‘Don’t let him touch a mathematical book till he is seventeen.’ Instead, he suggested stimulating the boy’s literary skills so that when eventually he returned to mathematics he would be able to write with his own mathematical voice and not one he had picked up from the books of the day.
It proved to be sound advice. Cauchy developed a new voice that was irrepressible once the floodgates protecting Cauchy from the outside world had been reopened. Cauchy’s output grew to be so immense that the journal Comptes Rendus had to impose a page limit on articles it printed that is strictly adhered to even today. Cauchy’s new mathematical language was too much for some of his contemporaries. The Norwegian mathematician Niels Henrik Abel wrote in 1826, ‘Cauchy is mad … what he does is excellent but very muddled. At first I understood practically none of it; now I see some of it more clearly.’ Abel goes on to observe that of all the mathematicians in Paris, Cauchy was the only one doing ‘pure mathematics’ whilst others ‘busy themselves exclusively with magnetism and other physical subjects … he is the only one who knows how mathematics should be done’.
Cauchy was to land himself in trouble with the authorities in Paris for steering students away from practical applications of mathematics. The director of the École Polytechnique, where Cauchy was lecturing, wrote to him criticising him for his obsession with abstract mathematics: ‘It is the opinion of many persons that instruction in pure mathematics is being carried too far at the École and that such an uncalled for extravagance is prejudicial to the other branches.’ So it was perhaps no wonder that Cauchy’s work would be appreciated by the young Riemann.
So exciting were these new ideas that Riemann almost became a recluse. His contemporaries were to see nothing of him while he waded through Cauchy’s output. Several weeks later Riemann resurfaced, declaring that ‘this is a new mathematics’. What had captured Cauchy and Riemann’s imagination was the emerging power of imaginary numbers.
Imaginary numbers – a new mathematical vista
The square root of minus one, the building block of imaginary numbers, seems to be a contradiction in terms. Some say that admitting the possibility of such a number is what separates the mathematicians from the rest. A creative leap is required to gain access to this bit of the mathematical world. At first sight it looks as if it has nothing to do with the physical world. The physical world seems to be built on numbers whose square is always a positive number. Imaginary numbers, however, are more than just an abstract game. They hold the key to the twentieth-century world of subatomic particles. On a larger scale, aeroplanes would not have taken to the skies without engineers taking a journey through the world of imaginary numbers. This new world provides a flexibility denied to those who stick to ordinary numbers.
The story of how these new numbers were discovered begins with the need to solve simple equations. As the ancient Babylonians and Egyptians recognised, if seven fish were to be divided between three people, for example, fractional numbers –
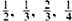
Fractions are the numbers whose decimal expansions have a repeating pattern. For example,
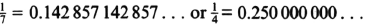
To capture the impossibility of expressing such numbers in any way other than as solutions to equations such as x2 = 2, mathematicians called them irrational numbers. The name reflected mathematicians’ sense of unease at their inability to write down precisely what these numbers were. Nevertheless, there was still a sense of the reality of these numbers since they could be seen as points marked on a ruler, or on what mathematicians call the number line. The square root of 2, for example, is a point somewhere between 1.4 and 1.5. If one could make a perfect Pythagorean right-angled triangle with the two short sides one unit long, then the location of this irrational number could be determined by laying the long side against the ruler and marking off the length.
The negative numbers were discovered similarly out of attempts to solve simple equations such as x + 3 = 1. Hindu mathematicians proposed these new numbers in the seventh century AD. Negative numbers were created in response to the growing world of finance, as they were useful for describing debt. It took European mathematicians another millennium before they were happy to admit the existence of such ‘fictitious numbers’, as they were called. Negative numbers took their place on the number line stretching out to the left of zero.
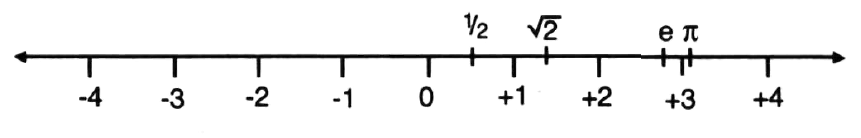
The real numbers – every fraction, negative number or irrational number is represented by a point on the number line.
Irrational numbers and negative numbers allow us to solve many different equations. Fermat’s equation x3 + y3 = z3 has interesting solutions if you don’t insist, as Fermat had, that x, y and z should be whole numbers. For example, we can choose x = 1 and y = 1, and put z equal to the cube root of 2 – and the equation is solved. But there were still other equations which couldn’t be solved in terms of any of the numbers on the number line.
There seemed to be no number which was a solution to the equation x2 = −1. After all, if you square a number, positive or negative, the answer is always positive. So any number that satisfies this equation is not going to be an ordinary number. But if the Greeks could imagine a number like the square root of 2, without being able to write it down as a fraction, mathematicians began to see that they could make a similar imaginative leap and create a new number to solve the equation x2 = −1. Such a creative jump marks one of the conceptual challenges for anyone learning mathematics. This new number, the square root of minus one, was called an imaginary number and given the symbol i. In contrast, mathematicians began to refer to the numbers that could be found on the number line as real numbers.
To create an answer to this equation, seemingly out of thin air, seems like cheating. Why not accept that the equation has no solution? That is one way forward, but mathematicians like to be more optimistic. Once we accept the idea that there is a new number that does solve this equation, the advantages of this creative step far outweigh any initial unease. Once named, its existence seems inevitable. It no longer feels like an artificially created number but a number that had been there all along, unobserved until we’d asked the right question. Eighteenth-century mathematicians had been loath to admit there could be any such numbers. Nineteenth-century mathematicians were brave enough to believe in new modes of thought which challenged the accepted ideas of what constituted the mathematical canon.
Frankly, the square root of −1 is as abstract a concept as the square root of 2. Both are defined as solutions to equations. But would mathematicians have to start creating new numbers for every new equation that came along? What if we want solutions to an equation like x4 = −1? Are we going to have to use more and more letters in our attempts to name all these new solutions? It was with some relief that Gauss finally proved, in his doctoral thesis of 1799, that no new numbers were needed. Using this new number i, mathematicians could finally solve any equation they might come across. Every equation had a solution that consisted of some combination of ordinary real numbers (the fractions and irrational numbers) and this new number, i.
The key to Gauss’s proof was to extend the picture we already had of ordinary numbers as lying on a number line: a line running east-west on which each point represents a number. These were the real numbers familiar to mathematicians since the Greeks. But there was no room on the line for this new imaginary number, the square root of −1. So Gauss wondered what would happen if you created a new direction. What if one unit north of the number line were used to represent i? All the new numbers that were needed to solve equations were combinations of i and ordinary numbers, for example 1 + 2i. Gauss realised that on this two-dimensional map there was a point corresponding to every possible number. The imaginary numbers then simply became coordinates on a map. The number 1 + 2i was represented by the point reached by travelling one unit east and two units north.
Gauss would interpret these numbers as sets of directions in his map of the imaginary world. To add two imaginary numbers A + Bi and C + Di just meant following two sets of directions, one after the other. For example, adding together 6 + 3i and 1 + 2i gets you to the location 7 + 5i.
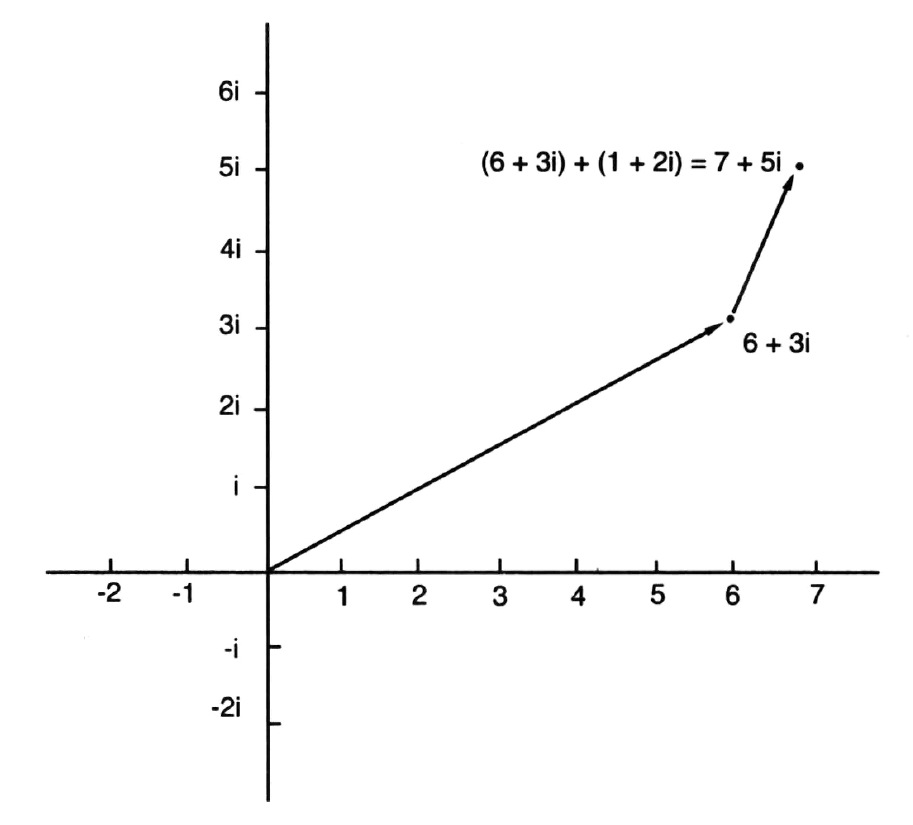
Following directions – how to add two imaginary numbers.
Although this was a very potent picture. Gauss was to keep his map of the imaginary world hidden from public view. Once he had built his proof, he removed the graphic scaffolding so that no trace of his vision remained. He was aware that pictures in mathematics were regarded with some suspicion during this period. The dominance of the French mathematical tradition during Gauss’s youth meant that the preferred pathway to the mathematical world was the language of formulas and equations, a language that went hand in hand with the utilitarian approach to the subject. There were also other reasons for this aversion to images.
For several hundred years, mathematicians had believed that pictures had the power to mislead. After all, the language of mathematics had been introduced to tame the physical world. In the seventeenth century, Descartes had attempted to turn the study of geometry into pure statements about numbers and equations. ‘Sense perceptions are sense deceptions’ was his motto. Riemann had come to dislike this denial of the physical picture when he’d been reading Descartes in the comfort of Schmalfuss’s library.
Mathematicians around the turn of the nineteenth century had been burnt by an erroneous pictorial proof of a formula describing the relationship between the number of corners, edges and faces of geometric solids. Euler had conjectured that if a solid has C corners, E edges and F faces, then the numbers C, E and F must satisfy the relationship C − E + F = 2. For example, a cube has 8 corners, 12 edges and 6 faces. The young Cauchy had himself constructed a ‘proof’ in 1811 based on pictorial intuition, but was rather shocked to be shown a solid which didn’t satisfy this formula – a cube with a hole at its centre.
The ‘proof’ had missed the possibility that a solid might contain such a hole. It was necessary to introduce an extra ingredient into the formula which kept track of the number of holes in the solid. Having been tricked by the power of pictures to hide perspectives that weren’t initially apparent, Cauchy sought refuge in the security that formulas seemed to provide. One of the revolutions he effected was to create a new mathematical language which allowed mathematicians to discuss the concept of symmetry in a rigorous way without the need for pictures.
Gauss knew that his secret map of imaginary numbers would be anathema to mathematicians at the end of the eighteenth century, so he omitted it from his proof. Numbers were things you added and multiplied, not drew pictures of. Gauss eventually came clean some forty years later about the scaffolding he had used in his doctorate.
Looking-glass world
Even without Gauss’s map, Cauchy and other mathematicians had begun to explore what happens if you extend the idea of functions to this new world of imaginary numbers rather than sticking to real numbers. To their surprise, these imaginary numbers opened up new connections between seemingly unrelated parts of the mathematical world.
A function is like a computer program in which you input one number, a calculation is made, and another number is output. The function might be defined by some simple equation like x2 + 1. When you input a number, for example 2, the function calculates 22 + 1 and outputs 5. Other functions are more complicated. Gauss was interested in the function that counted the number of primes. You input a number x, and the function tells you how many primes there are up to x. Gauss had denoted this function by π(x). The graph of this function is a climbing staircase, as shown on p. 50. Every time the input encounters a prime number, the output jumps another step. As x goes from 4.9 to 5.1, the number of primes increases from two to three to register the new prime, 5.





