
Полная версия
The Music of the Primes: Why an unsolved problem in mathematics matters
Fermat’s numbers were very dear to Gauss’s heart. The fact that 17 is one of Fermat’s primes is the key to why Gauss could construct his perfect 17-sided shape. In his great treatise Disquisitiones Arithmeticae, Gauss shows why it is that, if the Nth Fermat number is a prime, you can make a geometric construction of an N-sided shape only using a straight edge and compass. The fourth Fermat number, 65,537, is prime, so with these very basic instruments it is possible to construct a perfect 65,537-sided figure.
Fermat’s numbers have failed to throw up more than four primes to date, but he had more success in uncovering some of the very special properties that prime numbers have. Fermat discovered a curious fact about those prime numbers that leave remainder 1 on division by 4 – examples are 5, 13, 17 and 29. Such prime numbers can always be written as the sum of two squares – for example, 29 = 22 + 52. This was another of Fermat’s teases. Although he claimed to have a proof, he failed to record much of the details.
On Christmas Day, 1640, Fermat wrote of his discovery – that certain primes could be expressed as the sum of two squares – in a letter to a French monk called Marin Mersenne. Mersenne’s interests were not confined to liturgical matters. He loved music and was the first to develop a coherent theory of harmonics. He also loved numbers. Mersenne and Fermat corresponded regularly about their mathematical discoveries, and Mersenne broadcast many of Fermat’s claims to a wider audience. Mersenne became renowned for his role as an international scientific clearing house through which mathematicians could disseminate their ideas.
Just as generations had been captivated by the search for order in the primes, Mersenne too had caught the bug. Although he couldn’t see a way to find a formula that would produce all the primes, he did come across a formula that in the long run has proved far more successful at finding primes than Fermat’s formula has. Like Fermat, he started by considering powers of 2. But instead of adding 1, as Fermat had, Mersenne decided to subtract 1 from the answer. So, for example, 23 − 1 = 8 − 1 = 7, a prime number. Maybe Mersenne’s musical intuition was coming to his aid. Doubling the frequency of a note takes the note up an octave, so powers of 2 produce harmonic notes. You might expect a shift of 1 to sound a very dissonant note, not compatible with any previous frequency – a ‘prime note’.
Mersenne quickly discovered that his formula wasn’t going to yield a prime every time. For example, 24 − 1 = 15. Mersenne realised that if n was not prime then there was no chance that 2n − 1 was going to be prime. But now he boldly claimed that, for n up to 257, 2n − 1 would be prime precisely if n was one of the following numbers: 2, 3, 5, 7, 13, 19, 31, 67, 127, 257. He had discovered that even if n was prime, it still annoyingly didn’t guarantee that his number 2n − 1 would be prime. He could calculate 211 − 1 by hand and get 2,047, which is 23 × 89. Generations of mathematicians marvelled at Mersenne’s ability to assert that a number as large as 2257 − 1 was prime. This number has 77 digits. Did the monk have access to some mystical arithmetic formula that told him why this number, beyond any human computational abilities, was prime?
Mathematicians believe that if one continues Mersenne’s list, there will be infinitely many choices for n which will make Mersenne’s numbers 2n − 1 into prime numbers. But we are still missing a proof that this guess is true. We are still waiting for a modern day Euclid to prove that Mersenne’s primes never run dry. Or perhaps this far-off peak is just a mathematical mirage.
Many mathematicians of Fermat and Mersenne’s generation had played around with interesting numerological properties of the primes, but their methods did not match up to the ancient Greek ideal of proof. This explains in part why Fermat gave no details of many of the proofs he claimed to have discovered. There was a distinct lack of interest during this period in providing such logical explanations. Mathematicians were quite content with a more experimental approach to their subject, where in an increasingly mechanised world results were justified by their practical applications. In the eighteenth century, however, there arrived a mathematician who would rekindle a sense of the value of proof in mathematics. The Swiss mathematician Leonhard Euler, born in 1707, came up with explanations for many of the patterns that Fermat and Mersenne had discovered but failed to account for. Euler’s methods would later play a significant role in opening new theoretical windows onto our understanding of the primes.
Euler, the mathematical eagle
The mid-eighteenth century was a time of court patronage. This was pre-Revolutionary Europe, when countries were ruled by enlightened despots: Frederick the Great in Berlin, Peter the Great and Catherine the Great in St Petersburg, Louis XV and Louis XVI in Paris. Their patronage supported the academies that drove the intellectual development of the Enlightenment, and indeed they saw it as a mark of their standing that they be surrounded in their courts by intellectuals. And they were well aware of the potential of the sciences and mathematics to boost the military and industrial capabilities of their countries.
Euler was the son of a clergyman who hoped that his son would join him in the church. The young Euler’s precocious mathematical talents, however, had brought him to the notice of the powers that be. Euler was soon being courted by the academies throughout Europe. He had been tempted to join the Academy in Paris, which by this time had become the world’s centre of mathematical activity. He chose instead to accept an offer made to him in 1726 to join the Academy of Sciences in St Petersburg, the capstone for Peter the Great’s campaign to improve education in Russia. He would be joining friends from Basel who had stimulated his interest in mathematics as a child. They wrote to Euler from St Petersburg asking whether he could bring from Switzerland fifteen pounds of coffee, one pound of the best green tea, six bottles of brandy, twelve dozen fine tobacco pipes and a few dozen packs of playing cards. Laden down with gifts, it took the young Euler seven weeks to complete the long journey by boat, on foot and by post wagon, and in May 1727 he finally arrived in St Petersburg to pursue his mathematical dreams. His subsequent output was so extensive that the St Petersburg Academy was still publishing material that had been housed in their archives some fifty years after Euler’s death in 1783.
The role of the court mathematician is perfectly illustrated by a story that was told of Euler’s time in St Petersburg. Catherine the Great was hosting the famous French philosopher and atheist Denis Diderot. Diderot was always rather damning of mathematics, declaring that it added nothing to experience and served only to draw a veil between human beings and nature. Catherine, though, quickly tired of her guest, not because of Diderot’s disparaging views on mathematics but rather his tiresome attempts to rattle the religious faith of her courtiers. Euler was promptly called to court to assist in silencing the insufferable atheist. In appreciation of her patronage, Euler duly consented and addressed Diderot in serious tones before the assembled court: ‘Sir, (a + bn)/n = x, hence God exists; reply.’ Diderot is reported to have retreated in the light of such a mathematical onslaught.
This anecdote, told by the famous English mathematician Augustus De Morgan in 1872, had probably been embroidered for popular consumption and is a reflection more of the fact that most mathematicians enjoy putting down philosophers. But it does show how the royal courts of Europe had not considered themselves complete without a smattering of mathematicians amongst the ranks of astronomers, artists and composers.
Catherine the Great was interested not so much in mathematical proofs of the existence of God, but rather in Euler’s work on hydraulics, ship construction and ballistics. The Swiss mathematician’s interests ranged far and wide over the mathematics of the day. As well as military mathematics, Euler also wrote on the theory of music, but ironically his treatise was regarded as too mathematical for musicians and too musical for mathematicians.
One of his popular triumphs was the solution of the Problem of the Bridges of Königsberg. The River Pregel, known now as the Pregolya, runs through Königsberg, which in Euler’s day was in Prussia (it’s now in Russia, and called Kaliningrad). The river divides, creating two islands in the centre of the town, and the Königsbergers had built seven bridges to span it (see overleaf).
It had become a challenge amongst the citizens to see if anyone could walk around the town, crossing each bridge once and only once, and return to their starting point. It was Euler who eventually proved in 1735 that the task was impossible. His proof is often cited as the beginning of topology, where the actual physical dimensions of the problem are not relevant. It was the network of connections between different parts of the town that was important to Euler’s solution, and not their actual locations or distances apart – the map of the London Underground illustrates this principle.
It was numbers above all that captivated Euler’s heart. As Gauss would write:
The peculiar beauties of these fields have attracted all those who have been active there; but none has expressed this so often as Euler, who, in almost every one of his many papers on number-theory, mentions again and again his delight in such investigations, and the welcome change he finds there from tasks more directly related to practical applications.

The bridges of Konigsberg.
Euler’s passion for number theory had been stimulated by correspondence with Christian Goldbach, an amateur German mathematician who was living in Moscow and unofficially employed as secretary of the Academy of Sciences in St Petersburg. Like the amateur mathematician Mersenne before him, Goldbach was fascinated by playing around with numbers and doing numerical experiments. It was to Euler that Goldbach communicated his conjecture that every even number could be written as a sum of two primes. Euler in return would write to Goldbach to try out many of the proofs he had constructed to confirm Fermat’s mysterious catalogue of discoveries. In contrast to Fermat’s reticence in keeping his supposed proofs a secret from the world, Euler was happy to show off to Goldbach his proof of Fermat’s claim that certain primes can be written as the sum of two squares. Euler even managed to prove an instance of Fermat’s Last Theorem.
Despite his passion for proof, Euler was still very much an experimental mathematician at heart. Many of his arguments flew close to the mathematical wind, containing steps that weren’t completely rigorous. That did not concern him if it led to interesting new discoveries. He was a mathematician of exceptional computational skill and very adept at manipulating mathematical formulas until strange connections emerged. As the French academician François Arago observed, ‘Euler calculated without apparent effort, as men breathe, or eagles sustain themselves in the wind.’
Above all else, Euler loved calculating prime numbers. He produced tables of all the primes up to 100,000 and a few beyond. In 1732, he was also the first to show that Fermat’s formula for primes,
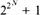
41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1,033, 1,097, 1,163, 1,231, 1,301, 1,373, 1,447, 1,523, 1,601
It seemed bizarre to Euler that you could generate so many primes with this formula. He realised that the process would have to break down at some point. It might already be clear to you that when you input 41, the output has to be divisible by 41. Also, for x = 40 you get a number which is not prime.
Nonetheless, Euler was quite struck by his formula’s ability to produce so many primes. He began to wonder what other numbers might work instead of 41. He discovered that in addition to 41 you could also choose q = 2, 3, 5, 11, 17, and the formula x2 + x + q would spit out primes when fed numbers from 0 to q − 2.
But finding such a simple formula for generating all the primes was beyond even the great Euler. As he wrote in 1751, ‘There are some mysteries that the human mind will never penetrate. To convince ourselves we have only to cast a glance at tables of primes and we should perceive that there reigns neither order nor rule.’ It seems paradoxical that the fundamental objects on which we build our order-filled world of mathematics should behave so wildly and unpredictably.
It would turn out that Euler had been sitting on an equation that would break the prime number deadlock. But it would take another hundred years, and another great mind, to show what Euler could not. That mind belonged to Bernhard Riemann. It was Gauss, though, who by initiating another of his classic lateral moves, would eventually inspire Riemann’s new perspective.
Gauss’s guess
If centuries of searching had failed to unearth some magic formula which would generate the list of prime numbers, perhaps it was time to adopt a different strategy. This was what the fifteen-year-old Gauss was thinking in 1792. He had been given a book of logarithms as a present the previous year. Until a few decades ago, tables of logarithms were familiar to every teenager doing calculations in the schoolroom. With the advent of pocket calculators, they lost their place as an essential tool in everyday life, but several hundred years ago every navigator, banker and merchant would have been exploiting these tables to turn difficult multiplication into simple addition. Included at the back of Gauss’s new book was a table of prime numbers. It was uncanny that primes and logarithms should appear together, because Gauss noticed after extensive calculations that there seemed to be a connection between these two seemingly unrelated topics.
The first table of logarithms was conceived in 1614 in an age when sorcery and science were bedfellows. Their creator, the Scottish Baron John Napier, was regarded by local residents as a magician who dealt in the dark arts. He skulked around his castle dressed in black, a jet-black cock perched on his shoulder, muttering that his apocalyptic algebra foretold that the Last Judgement would fall between 1688 and 1700. But as well as applying his mathematical skills to the practice of the occult, he also uncovered the magic of the logarithm function.
If you feed a number, say 100, into your calculator and then press the ‘log’ button, the calculator spits out a second number, the logarithm of 100. What your calculator has done is to solve a little puzzle: it has looked for the number x that makes the equation 10x = 100 correct. In this case the calculator outputs the answer 2. If we input 1,000, a number ten times larger than 100, then the new answer output by your calculator is 3. The logarithm goes up by 1. Here is the essential character of the logarithm: it turns multiplication into addition. Each time we multiply the input by 10, we get the new output by adding 1 to the previous answer.
It was a fairly major step for mathematicians to realise that they could talk about logarithms of numbers which weren’t whole-number powers of 10. For example, Gauss would have been able to look up in his tables the logarithm of 128 and find that raising 10 to the power 2.107 21 would get him pretty close to 128. These calculations are what Napier had collected together in the tables that he had produced in 1614.
Tables of logarithms helped to accelerate the world of commerce and navigation that was blossoming in the seventeenth century. Because of the dialogue that logarithms created between multiplication and addition, the tables helped to convert a complicated problem of multiplying together two large numbers into the simpler task of adding their logarithms. To multiply together large numbers, merchants would add together the logarithms of the numbers and then use the log tables in reverse to find the result of the original multiplication. The increase in speed that the sailor or seller would gain via these tables might save the wrecking of a ship or the collapse of a deal.
But it was the supplementary table of prime numbers at the back of his book of logarithms that fascinated the young Gauss. In contrast to the logarithms, these tables of primes were nothing more than a curiosity to those interested in the practical application of mathematics. (Tables of primes constructed in 1776 by Antonio Felkel were considered so useless that they ended up being used for cartridges in Austria’s war with Turkey!) The logarithms were very predictable; the primes were completely random. There seemed no way to predict when to expect the first prime after 1,000, for example.
The important step Gauss took was to ask a different question. Rather than attempting to predict the precise location of the next prime, he tried instead to see whether he could at least predict how many primes there were in the first 100 numbers, the first 1,000 numbers, and so on. If one took any number N, was there a way to estimate how many primes one would expect to find amongst the numbers from 1 to N? For example, there are twenty-five prime numbers up to 100. So you have a one in four chance of getting a prime if you choose a number at random between 1 and 100. How does this proportion change if we look at the primes from 1 to 1000, or 1 to 1,000,000? Armed with his prime number tables, Gauss began his quest. As he looked at the proportion of numbers that were prime, he found that when he counted higher and higher a pattern started to emerge. Despite the randomness of these numbers, a stunning regularity seemed to be looming out of the mist.
If we look at the table overleaf of values of the number of primes up to various powers of ten, based on more modern calculations, this regularity becomes apparent.
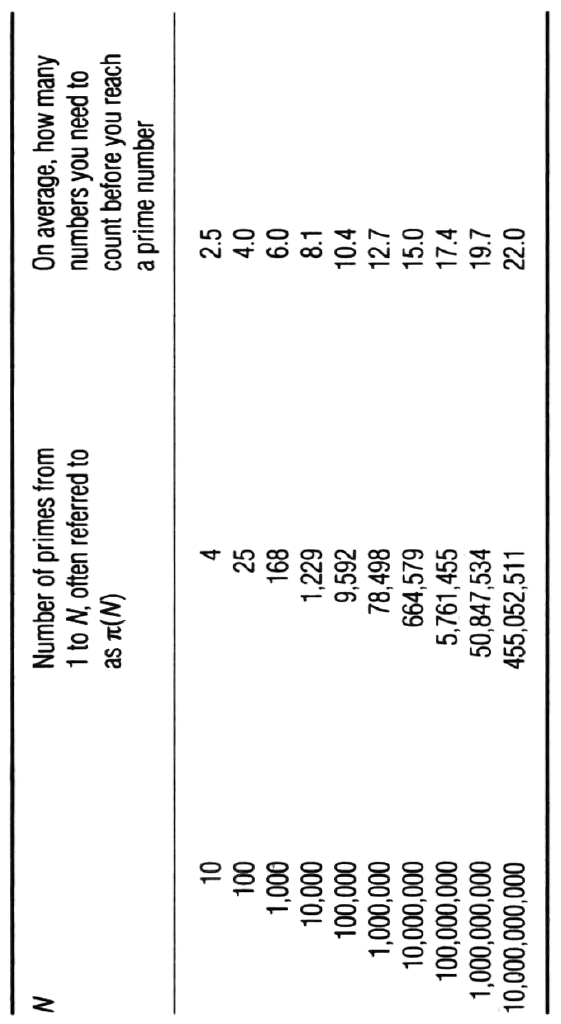
This table, which contains much more information than was available to Gauss, shows us more clearly the regularity that Gauss discovered. It is in the last column that the pattern manifests itself. This column represents the proportion of prime numbers amongst all the numbers being considered. For example, 1 in 4 numbers are prime counting up to 100, so in that interval you will need to count, on average, 4 to get from one prime to the next. Of the numbers up to 10 million, 1 in 15 are prime. (So, for example, there is a 1 in 15 chance that a seven-digit telephone number is a prime.) For N greater than 10,000, this last column seems to be just increasing by about 2.3 each time.
So every time Gauss multiplied by 10, he had to add about 2.3 to the ratio of the primes to all the numbers. This link between multiplication and addition is precisely the relationship embodied in a logarithm. Gauss, with his book of logarithms, would have found this connection staring him in the face.
The reason why the proportion of primes was increasing by 2.3 rather than 1 every time Gauss multiplied by 10 is because primes favour logarithms based not on powers of 10 but on powers of a different number. Pressing the ‘log’ button on your calculator when you input 100 produced the answer 2, which is the solution to the equation 10x = 100. But there is nothing that says we have to have 10 as the number to raise to the power x. It is our obsession with our ten fingers which makes 10 so appealing. The choice of the number 10 is called the base of the logarithm. We can talk about the logarithm of a number to a base other than 10. For example, the logarithm of 128 to base 2 rather than base 10 requires us to solve a different puzzle, to find a number x so that 2x = 128. If we had a ‘log to base 2’ button on our calculator, we could press it and get the answer 7, because we need to raise 2 to the power of 7 to get up to 128: 27 = 128.
What Gauss discovered is that primes can be counted using logarithms to the base of a special number, called e, which to twelve decimal places is 2.718 281 828459 … (like π, it has an infinite decimal expansion with no repeating patterns), e turns out to be as important in mathematics as the number π, and occurs all over the mathematical world. This is why logarithms to the base e are called ‘natural’ logarithms.
The table that Gauss had made at the age of fifteen led him to the following guess. For the numbers from 1 to N roughly 1 out of every log(N) numbers will be prime (where log(N) denotes the logarithm of N to the base e). He could then estimate the number of primes from 1 to N as roughly N/log(N). Gauss was not claiming that this magically gave him an exact formula for the number of primes up to N – it just seemed to provide a very good ballpark estimate.
It was a similar philosophy that he would later apply in his rediscovery of Ceres. His astronomical method made a good prediction for a small region of space to look at, given the data that had been recorded. Gauss had taken the same approach for the primes. Generations had become obsessed with trying to predict the precise location of the next prime, with producing formulas that would generate prime numbers. By not getting hung up on the minutiae of which number was prime or not, Gauss had hit on some sort of pattern. By stepping back and asking the broader question of how many primes there are up to a million rather than precisely which numbers are prime, a strong regularity seemed to emerge.
Gauss had made an important psychological shift in looking at the primes. It was as if previous generations had listened to the music of the primes note by note, unable to hear the whole composition. By concentrating instead on counting how many primes there were as one counted higher, Gauss found a new way to hear the dominant theme.
Following Gauss, it has become customary to denote the number of primes we find in the numbers from 1 to N by the symbol π(N) (this is just a name for this count and has nothing to do with the number π). It is perhaps unfortunate that Gauss used a symbol that makes one think of circles and the number 3.1415 … Think of this instead as a new button on your calculator. You input a number N and press the π(N) button, and the calculator outputs the number of primes up to N. So, for example, π(100) = 25, the number of primes up to 100, and π(1,000) = 168.
Notice that you can still use this new ‘count primes’ button to identify precisely when you get a prime. If you input the number 100 and press this button, counting primes between 1 and 100, you get the answer 25. If you now input the number 101, the answer will go up by 1 to 26 primes, and this means that 101 is a new prime number. So whenever there is a difference between π(N) and π(N +1), you know that N + 1 must be a new prime.
To reveal quite how stunning Gauss’s pattern was, we can look at a graph of the function π(N) counting the number of primes from 1 to N. Here’s a graph of π(N) for numbers N from 1 to 100:





