The Music of the Primes: Why an unsolved problem in mathematics matters

Mathematicians soon realised that some of these functions, such as the one built from the equation x2 + 1, could be fed with imaginary numbers as well as ordinary numbers. For example, input x = 2i into the function, and the output is calculated as (2i)2 + 1 = −4 + 1 = −3. The feeding of functions with imaginary numbers had begun in Euler’s generation. As early as 1748, Euler had stumbled across strange connections between unrelated bits of mathematics by taking a trip through this looking-glass world. Euler knew that when you fed the exponential function 2x with ordinary numbers x, you got a graph that climbed rapidly. But when he fed the function with imaginary numbers he got a rather unexpected answer. Instead of the exponentially climbing graph, he started to see undulating waves of the type we now associate with, for example, sound waves. The function that produces these undulating waves is called the sine function. The image of the sine function is a familiar repeating curve where every 360 degrees we see the same shape appearing. The sine function is now used in a host of everyday calculations. For example, it can be used to measure the height of a building from ground level by measuring angles. It was Euler’s generation who discovered that these sine waves were also the key to reproducing musical sounds. A pure note like the A produced by a tuning fork used to tune a piano can be represented by such a wave.

Euler fed imaginary numbers into the function 2x. To his surprise, out came waves which corresponded to a particular musical note. Euler showed that the character of each note depended on the coordinates of the corresponding imaginary number. The farther north one is, the higher the pitch. The farther east, the louder the volume. Euler’s discovery was the first inkling that these imaginary numbers might open up unexpected new paths through the mathematical landscape. Following Euler, mathematicians began travelling out to this new-found land of imaginary numbers. The search for new connections would become infectious.

Riemann returned to Göttingen in 1849 in order to complete his doctoral thesis for Gauss’s consideration. That was the year in which Gauss wrote to his friend Encke of his childhood discovery of the connection between primes and logarithms. Although Gauss probably discussed his discovery with members of the faculty in Göttingen, prime numbers were not yet on Riemann’s mind. He was buzzing with the new mathematics from Paris, keen to explore the strange emerging world of functions fed with imaginary numbers.

Cauchy had begun the task of making a rigorous subject out of Euler’s first tentative steps into this new territory. Whilst the French were masters of equations and formulaic manipulation, Riemann was ready to capitalise on the German education system’s return to a more conceptual view of the world. By November 1851, his ideas had crystallised and he submitted his dissertation to the faculty in Göttingen. His ideas obviously struck a chord with Gauss. He greeted Riemann’s doctorate as evidence ‘of a creative, active, truly mathematical mind, and of a gloriously fertile originality’.

Riemann wrote to his father, keen to tell him about the progress he was making: ‘I believe I have improved my prospects with my dissertation. I hope also to learn to write more quickly and more fluently in time, especially if I mingle in society.’ But academic life in Göttingen did not at first live up to the thrills of Berlin. It was a somewhat stuffy, insular university, and Riemann lacked the confidence to engage with the old intellectual hierarchy. There were fewer students in Göttingen with whom he could relate. He was mistrustful of other people and never really at ease in a social environment. ‘He has done the strangest things here only because he believes that nobody can bear him,’ wrote his contemporary Richard Dedekind. Riemann was a hypochondriac and susceptible to bouts of depression. He hid his face behind the security of an increasingly large black beard. He was extremely anxious about his finances, surviving on the uncertainty of half a dozen voluntary students’ fees. The workload he undertook combined with the pressures of poverty led to a temporary breakdown in 1854. However, his mood would lighten whenever Dirichlet, the star of the Berlin mathematical tradition, visited Göttingen.

One professor in Göttingen with whom Riemann did manage to strike up a friendship was the eminent physicist Wilhelm Weber. Weber had collaborated on numerous projects with Gauss during their time together in Göttingen. They became a scientific Sherlock Holmes and Dr Watson, Gauss providing the theoretical underpinning which Weber then put into practice. One of their most famous inventions was to realise the potential of electromagnetism to communicate over a distance. They successfully rigged up a telegraph line between Gauss’s observatory and Weber’s laboratory over which they exchanged messages.

Although Gauss thought the invention a curiosity, Weber saw clearly what their discovery would unleash. ‘When the globe is covered with a net of railroads and telegraph wires,’ he wrote, ‘this net will render services comparable to those of the nervous system in the human body, partly as a means of transport, partly as a means for the propagation of ideas and sensations with the speed of lightning.’ The rapid spread of the telegraph, together with the later implementation of Gauss’s invention of the clock calculator in computer security, make Gauss and Weber the grandfathers of e-business and the Internet. Their collaboration is immortalised in a statue of the pair in the city of Göttingen.

One visitor to Weber in Göttingen paints a typical picture of a slightly mad inventor: ‘a curious little fellow who speaks in a shrill, unpleasant and hesitating voice. He speaks and stutters unceasingly; one has nothing to do but to listen. Sometimes he laughs for no earthly reason, and one feels sorry at not being able to join him.’ Weber had a little more of the rebel in him than his collaborator Gauss. He had been one of the ‘Göttingen Seven’ temporarily dismissed from the faculty for protesting at the arbitrary rule of the Hanoverian king in 1837. For some time after completing his thesis, Riemann worked as Weber’s assistant. During this apprenticeship Riemann developed a soft spot for Weber’s daughter, but his advances were not reciprocated.

In 1854, Riemann wrote to his father that ‘Gauss is seriously ill and the physicians fear that his death is imminent.’ Riemann was worried that Gauss might die before examining his habilitation, the degree required to become a professor at a German university. Fortunately Gauss lived long enough to hear Riemann’s ideas on geometry and its relationship to physics that had germinated during his work with Weber. Riemann was convinced that the fundamental questions of physics could all be answered using mathematics alone. The developments in physics over the ensuing years would eventually confirm his faith in mathematics. Riemann’s theory of geometry is regarded by many as one of his most significant contributions to science, and it would be one of the planks in the platform from which Einstein launched his scientific revolution at the beginning of the twentieth century.

A year later, Gauss died. Although the man had passed, his ideas were to keep mathematicians busy for generations to come. He had left behind his conjectured connection between primes and the logarithm function for the next generation to chew over. Astronomers immortalised the great man in the heavens by naming an asteroid Gaussia. And in the University of Göttingen’s anatomical collection one can even find Gauss’s brain, pickled for eternity, which was reported to be more richly convoluted than any brain previously dissected.

Dirichlet, whose lectures Riemann had attended in Berlin, was appointed to Gauss’s vacant chair. Dirichlet was to bring to Göttingen some of the intellectual excitement that Riemann had enjoyed when he was in Berlin. An English mathematician recorded the impression that a visit to Dirichlet in Göttingen made on him at this time: ‘He is rather tall, lanky-looking man with moustache and beard about to turn grey … with a somewhat harsh voice and rather deaf: it was early, he was unwashed and unshaved and with his schlafrock [dressing gown], slippers, cup of coffee and cigar.’ Despite this Bohemian exterior, there burned inside him a desire for rigour and proof that was unequalled at the time. His contemporary in Berlin, Carl Jacobi, wrote to Dirichlet’s first patron Alexander von Humboldt that ‘Only Dirichlet, not I, nor Cauchy, not Gauss, knows what a perfectly rigorous proof is, but we learn it only from him. When Gauss says he has proved something, I think it is very likely; when Cauchy says it, it is a fifty-fifty bet; when Dirichlet says it, it is certain.’

The arrival of Dirichlet in Göttingen began to shake the social fabric of the town. Dirichlet’s wife, Rebecka, was the sister of the composer Felix Mendelssohn. Rebecka loathed the dull Göttingen social scene and threw numerous parties trying to reproduce the Berlin salon atmosphere she had been forced to leave behind.

Dirichlet’s less formal approach to the educational hierarchy meant that Riemann was able to discuss mathematics openly with the new professor. Riemann had become rather isolated on his return from Berlin to Göttingen. The combination of Gauss’s austere personality in later life and Riemann’s shyness meant that Riemann had discussed little with the great master. By contrast, Dirichlet’s relaxed manner was perfect for Riemann who, in an atmosphere more conducive to discussion, began to open up. Riemann wrote to his father about his new mentor: ‘Next morning Dirichlet was with me for two hours. He read over my dissertation and was very friendly – which I could hardly have expected considering the great distance in rank between us.’

In turn, Dirichlet appreciated Riemann’s modesty and also recognised the originality of his work. On occasions Dirichlet even managed to drag Riemann away from the library to join him on walks in the countryside around Göttingen. Almost apologetically, Riemann wrote to his father explaining that these escapes from mathematics did him more good scientifically than if he had stayed at home poring over his books. It was during one of his discussions with Riemann whilst walking through the woods of Lower Saxony that Dirichlet inspired Riemann’s next move. It would open up a whole new perspective on the primes.

The zeta function – the dialogue between music and mathematics

During his years in Paris in the 1820s, Dirichlet had become fascinated by Gauss’s great youthful treatise Disquisitiones Arithmeticae. Although Gauss’s book marked a beginning of number theory as an independent discipline, the book was difficult and many failed to penetrate the concise style Gauss preferred. Dirichlet, though, was more than happy to battle with one tough paragraph after another. At night he would place the book under his pillow in the hope that the next morning’s reading would suddenly make sense. Gauss’s treatise has been described as a ‘book of seven seals’, but thanks to the labours and dreams of Dirichlet, those seals were broken and the treasures within gained the wide distribution they deserved.

Dirichlet was especially interested in Gauss’s clock calculator. In particular, he was intrigued by a conjecture that went back to a pattern spotted by Fermat. If you took a clock calculator with N hours on it and you fed in the primes, then, Fermat conjectured, infinitely often the clock would hit one o’clock. So, for example, if you take a clock with 4 hours there are infinitely many primes which Fermat predicted would leave remainder 1 on division by 4. The list begins 5, 13, 17, 29, …

In 1838, at the age of thirty-three, Dirichlet had made his mark in the theory of numbers by proving that Fermat’s hunch was indeed correct. He did this by mixing ideas from several areas of mathematics that didn’t look as if they had anything to do with one another. Instead of an elementary argument like Euclid’s cunning proof that there are infinitely many primes, Dirichlet used a sophisticated function that had first appeared on the mathematical circuit in Euler’s day. It was called the zeta function, and was denoted by the Greek letter ζ. The following equation provided Dirichlet with the rule for calculating the value of the zeta function when fed with a number x:

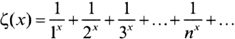
To calculate the output at x, Dirichlet needed to carry out three mathematical steps. First, calculate the exponential numbers 1x, 2x, 3x, …, nx, … Then take the reciprocals of all the numbers produced in the first step. (The reciprocal of 2x is 1/2x.) Finally, add together all the answers from the second step.

It is a complicated recipe. The fact that each number 1, 2, 3, … makes a contribution to the definition of the zeta function hints at its usefulness to the number theorist. The downside comes in having to deal with an infinite sum of numbers. Few mathematicians could have predicted what a powerful tool this function would become as the best way to study the primes. It was almost stumbled upon by accident.

The origins of mathematicians’ interest in this infinite sum came from music and went back to a discovery made by the Greeks. Pythagoras was the first to discover the fundamental connection between mathematics and music. He filled an urn with water and banged it with a hammer to produce a note. If he removed half the water and banged the urn again, the note had gone up an octave. Each time he removed more water to leave the urn one-third full, then one-quarter full, the notes produced would sound to his ear in harmony with the first note he’d played. Any other notes which were created by removing some other amount of water sounded in dissonance with that original note. There was some audible beauty associated with these fractions. The harmony that Pythagoras had discovered in the numbers

made him believe that the whole universe was controlled by music, which is why he coined the expression ‘the music of the spheres’.

Ever since Pythagoras’ discovery of an arithmetic connection between mathematics and music, people have compared both the aesthetic and the physical traits shared by the two disciplines. The French Baroque composer Jean-Philippe Rameau wrote in 1722 that ‘Not withstanding all the experience I may have acquired in music from being associated with it for so long, I must confess that only with the aid of mathematics did my ideas become clear.’ Euler sought to make music theory ‘part of mathematics and deduce in an orderly manner, from correct principles, everything which can make a fitting together and mingling of tones pleasing’. Euler believed that it was the primes that lay behind the beauty of certain combinations of notes.

Many mathematicians have a natural affinity with music. Euler would relax after a hard day’s calculating by playing his clavier. Mathematics departments invariably have little trouble assembling an orchestra from the ranks of their members. There is an obvious numerical connection between the two given that counting underpins both. As Leibniz described it, ‘Music is the pleasure the human mind experiences from counting without being aware that it is counting.’ But the resonance between the subjects goes much deeper than this.

Mathematics is an aesthetic discipline where talk of beautiful proofs and elegant solutions is commonplace. Only those with a special aesthetic sensibility are equipped to make mathematical discoveries. The flash of illumination that mathematicians crave often feels like bashing notes on a piano until suddenly a combination is found which contains an inner harmony marking it out as different.

G.H. Hardy wrote that he was ‘interested in mathematics only as a creative art’. Even for the French mathematicians in Napoleon’s academies, the buzz of doing mathematics came not from its practical application but from its inner beauty. The aesthetic experiences of doing mathematics or listening to music have much in common. Just as you might listen to a piece of music over and over and find new resonances previously missed, mathematicians often take pleasure in re-reading proofs in which the subtle nuances that make it hang together so effortlessly gradually reveal themselves. Hardy believed that the true test of a good mathematical proof was that ‘the ideas must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics.’ For Hardy, ‘A mathematical proof should resemble a simple and clear-cut constellation, not a scattered Milky Way.’

Both mathematics and music have a technical language of symbols which allow us to articulate the patterns we are creating or discovering. Music is much more than just the minims and crochets which dance across the musical stave. Similarly, mathematical symbols come alive only when the mathematics is played with in the mind.

As Pythagoras discovered, it is not just in the aesthetic realm that mathematics and music overlap. The very physics of music has at its root the basics of mathematics. If you blow across the top of a bottle you hear a note. By blowing harder, and with a little skill, you can start to hear higher notes – the extra harmonics, the overtones. When a musician plays a note on an instrument they are producing an infinity of additional harmonics, just as you do when you blow across the top of the bottle. These additional harmonics help to give each instrument its own distinctive sound. The physical characteristics of each instrument mean that we hear different combinations of harmonics. In addition to the fundamental note, the clarinet plays only those harmonics produced by odd fractions:

, … The string of a violin, on the other hand, vibrates to create all the harmonics that Pythagoras produced with his urn – those corresponding to the fractions

, …

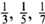
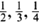
Since the sound of a vibrating violin string is the infinite sum of the fundamental note and all the possible harmonics, mathematicians became intrigued by the mathematical analogue. The infinite sum

… became known as the harmonic series. This infinite sum is also the answer Euler got when he fed the zeta function with the number x = 1. Although this sum grew only very slowly as he added more terms, mathematicians had known since the fourteenth century that eventually it must spiral off to infinity.

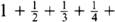
So the zeta function must output the answer infinity when fed the number x = 1. If, however, instead of taking x = 1, Euler fed the zeta function with a number bigger than 1, the answer no longer spiralled off to infinity. For example, taking x = 2 means adding together all the squares in the harmonic series:

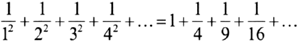
This is a smaller number as it does not include all possible fractions found when x = 1. We are now adding only some of the fractions, and Euler knew that this time the smaller sum wouldn’t spiral off to infinity but would home in on some particular number. It had become quite a challenge by Euler’s day to identify a precise value for this infinite sum when x = 2. The best estimate was somewhere around

. In 1735, Euler wrote that ‘So much work has been done on the series that it seems hardly likely that anything new about them may still turn up … I, too, in spite of repeated effort, could achieve nothing more than approximate values for their sums.’

Nevertheless, Euler, emboldened by his previous discoveries, began to play around with this infinite sum. Twisting it this way and that like the sides of a Rubik’s cube, he suddenly found the series transformed. Like the colours on the cube, these numbers slowly came together to form a completely different pattern from the one he had started with. As he went on to describe, ‘Now, however, quite unexpectedly, I have found an elegant formula depending upon the quadrature of the circle’ – in modern parlance, a formula depending on the number π = 3.1415 …

By some pretty reckless analysis, Euler had discovered that this infinite sum was homing in on the square of π divided by 6:

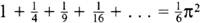
The decimal expansion of

, like that of π, is completely chaotic and unpredictable. To this day, Euler’s discovery of this order lurking in the number

ranks as one of the most intriguing calculations in all of mathematics, and it took the scientific community of Euler’s time by storm. No one had predicted a link between the innocent sum

and the chaotic number π.

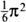
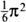
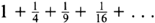
This success inspired Euler to investigate the power of the zeta function further. He knew that if he fed the zeta function with any number bigger than 1, the result would be some finite number. After a few years of solitary study he managed to identify the output of the zeta function for every even number. But there was something rather unsatisfactory about the zeta function. Whenever Euler fed the formula for the zeta function with any number less than 1, it would always output infinity. For example, for x = −1 it yields the infinite sum 1 + 2 + 3 + 4 + … The function behaved well only for numbers bigger than 1.

Euler’s discovery of his expression for

in terms of simple fractions was the first sign that the zeta function might reveal unexpected links between seemingly disparate parts of the mathematical canon. The second strange connection that Euler discovered was with an even more unpredictable sequence of numbers.

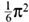
Rewriting the Greek story of the primes

Prime numbers suddenly enter Euler’s story as he tried to put his rickety analysis of the expression for

on a sound mathematical footing. As he played with the infinite sums he recalled the Greek discovery that every number can be built from multiplying prime numbers together, and realised that there was an alternative way to write the zeta function. He spotted that every term in the harmonic series, for example

, could be dissected using the knowledge that every number is built from its prime building blocks. So he wrote

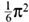
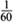
Instead of writing the harmonic series as an infinite addition of all the fractions, Euler could take just fractions built from single primes, like

, and multiply them together. His expression, known today as Euler’s product, connected the worlds of addition and multiplication. The zeta function appeared on one side of the new equation and the primes on the other. In one equation was encapsulated the fact that every number can be built by multiplying together prime numbers: