Гравитация и эфир

второй – от

до

,

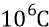
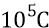
третий – от

до

,

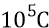
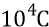
четвёртый – от

до

,

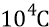
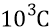
пятый – от

до

,

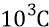
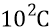
шестой – от

до

,

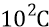
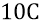
седьмой – от

до

,

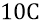
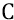
восьмой – от

до 0.

Мы, в состоянии «сейчас», находимся в последнем – восьмом дискрете. Стадия равноускоренного замедления – это тот период в жизни Большой Вселенной, когда радиальная скорость электромагнитной области квантов эфира замедляется относительно неподвижного преонного вакуума от величины

до величины меньшей единицы скорости света. Всё это замедление осуществляется только гравитацией; электромагнетизм здесь пока ещё не работает в полной мере по всем возможным направлениям, так как взаимные скорости квантов эфира, движущихся в радиальных направлениях движения тела Метагалактики, пока ещё превышают две единицы скорости света, то есть превышают ту величину взаимных скоростей квантов, когда они (при понижении скорости) начинают «видеть» друг друга уже электромагнетизмом, вступая, наконец-то, в электромагнитные взаимодействия друг с другом.

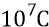
На самом же деле процессы электромагнитных взаимодействий начинаются «чуть раньше» – тогда, когда скорости квантов падают до величины «две единицы скорости света». Здесь взаимодействие начинает происходить только между теми квантами, которые пересекают трассы друг друга ортогонально (перпендикулярно). Тогда возникает, хотя и самое слабое пока, но отклонение трассы одной частицы электромагнитным взаимодействием другой. С этого же момента начинается непосредственное зарождение «тяжёлого» вакуума Метагалактик, как процесса медленно-постепенной закрутки квантов эфира вокруг уже готовых, хотя и слабых пока, но сгустков элементарных частиц, собранных в эти сгустки «местной» гравитацией. Если говорить более точно, то здесь начинается процесс сохранения высокой энергии «тяжёлых» квантов эфира. Тогда как процесс уменьшения энергии остальных квантов Скорлупы Вселенной продолжается. Он будет продолжаться до тех пор, пока собственная частота остальных («лёгких») квантов не упадёт на 5 порядков величины относительно собственной частоты тяжёлых квантов.

Определим средний коэффициент замедления скорости расширения Скорлупы для дискрета скорости, изменяющейся на порядок её величины. Вычисления сделаем на любом простом примере типа следующего. Разобьём дискрет на 10 частей равного времени. Пусть за первый отрезок времени из этих 10-ти тело, двигаясь пока со скоростью 10 единиц в секунду, прошло путь в 10 единиц расстояния. В следующий отрезок, двигаясь со скоростью 9 единиц, оно прошло путь в 9 единиц и так далее. Тогда за все 10 отрезков телом будет пройден путь:

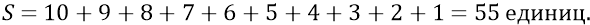
Следовательно, средняя скорость на этом дискрете из 10-ти отрезков времени составит величину:

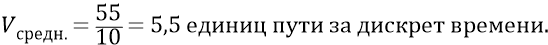
Тогда к концу всех 8-ми дискретов замедления расширяющаяся Скорлупа Большой Вселенной преодолеет путь:

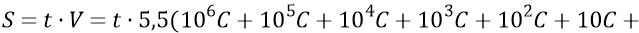
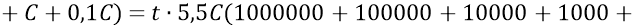
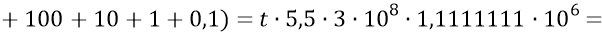
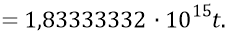
Приравняем теперь этот путь к найденному пути замедления Вселенной:

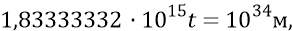
откуда время стадии замедления,

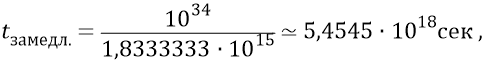
или

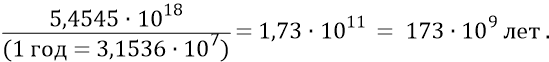
И тогда конечное время расширения эфирного тела Вселенной:

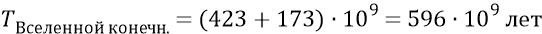
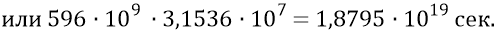
Время каждого из 8-ми интервалов замедления:

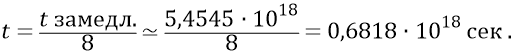
Сейчас мы можем находиться, например, в середине последнего, восьмого, интервала расширения Вселенной, где всё ещё двигаясь от центра Большого Взрыва со скоростью 0,55С, можем пролететь в течение половины интервала времени,

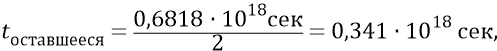
оставшийся путь в направлении – «от центра»:

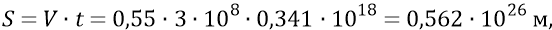
что на порядок уступает размерам Метагалактики. Но мы, вместе с Нашей Метагалактикой, его пройдём, продолжая замедляться, за время:

миллиардов лет, то есть за период более чем вдвое превышающий время существования планеты «Земля».

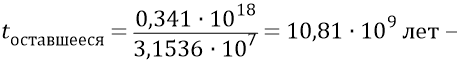
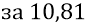
Время «сейчас» с момента начала замедления:

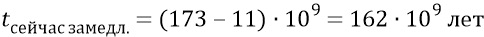
И тогда время, прошедшее с момента Большого Взрыва:

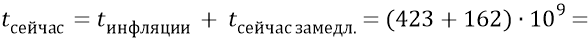
Если в конечное время расширения Скорлупы её конечная скорость расширения станет нулевой, то из уравнения

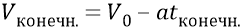
найдём ускорение электромагнитной Скорлупы Вселенной «

»:

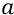
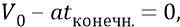
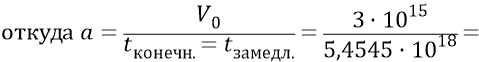
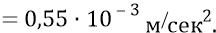
То есть электромагнитная Скорлупа Нашей Вселенной замедлялась с ускорением (с потерей скорости)

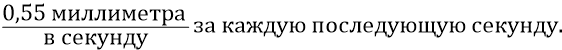
Итак, следуя рассмотренной кинематике, мы можем считать, что находимся по времени от момента расширения Вселенной на отметке

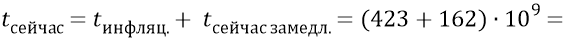
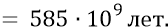
И поскольку мы уже оценили порядок ускорения (

, то ту же задачу вполне можем решать, пользуясь не нашим «методом на пальцах», однако – вполне понятном школьнику, но можем пользоваться «цивилизованной» формулой равнозамедленного движения (материальной точки), хорошо знакомой тому же школьнику:

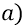
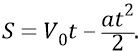
Здесь знак замедления скорости тела уже указан («минус»). Поэтому знак самого ускорения (

) – положителен. Причём эту формулу можно применять до момента остановки радиального расширения луча трассы тела (

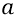
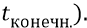
Почему для решения данной задачи мы вправе использовать именно эту формулу – равнозамедленного движения? Потому что фактически «подбрасываем вверх», допустим, эфирное тело Метагалактики в потенциальном гравитационном поле Большой Вселенной, по аналогии с тем, как подбрасываем камень в потенциальном гравитационном поле Земли. И при этом мы помним ещё со школы, что кинематика этой последней задачи вполне определяется данной формулой.

Сейчас мы можем попробовать определить, на каком расстоянии от момента начала замедления мы находимся «сейчас» (

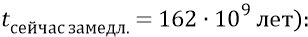
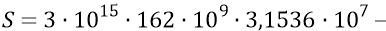
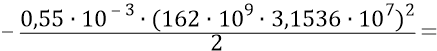
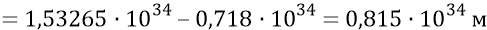
(при полном пути замедления

), что, в первом приближении, не противоречит разработанной ранее концепции).

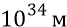
Сейчас (чуть ниже) мы приведём 2 варианта периодов замедления Вселенной, рассчитанных по формуле равнозамедленного движения точки на пути S, при двух различных значениях ускорения «

». Эти примеры покажут, что мы, с полученными цифрами, находимся в допустимом «коридоре» возможных значений ускорений и периодов. Например, стоит нам сейчас слегка уменьшить цифру ускорения «

» (до 0,41∙

как мы окажемся именно в той точке пути, соответствующей найденному ранее значению пути, оставшегося до полного замедления, но найденного с помощью довольно грубого иллюстративного метода «на пальцах».

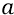
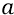
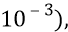
Вообще говоря, делая первые прикидки раздувающейся Вселенной, мы находимся сейчас в жутких условиях полнейших неопределённостей. Конечно, некоторые данные нам удалось добыть в ходе многолетней работы. И за целый ряд исходных данных мы готовы «поручиться» потому, что они довольно хорошо и даже по-своему красиво вписываются в физическую природу вещей. Однако на их основе всё же не получается сколько-нибудь «достоверно» оценить ряд других данных, необходимых для грамотного расчёта такого физического объекта, каким является Большая Вселенная. В этом смысле, попробуем привести некоторые примеры, способные красноречиво подчеркнуть, каков может быть разброс характеристик Вселенной при некоторых изменениях её начальных условий, но при изменениях, вполне вписывающихся в закон Здравого Смысла.

При данном конечном отрезке стадии замедления Вселенной и нулевой конечной радиальной скорости эфирной Скорлупы, из уравнения

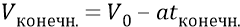
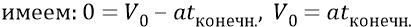
Вариант 1:

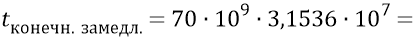
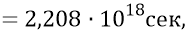
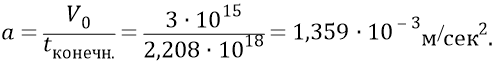
Вариант 2:

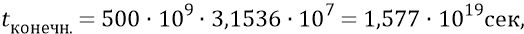
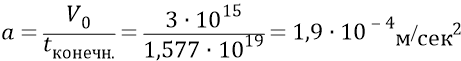
(у нас

лет при

).

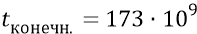
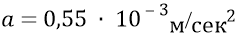
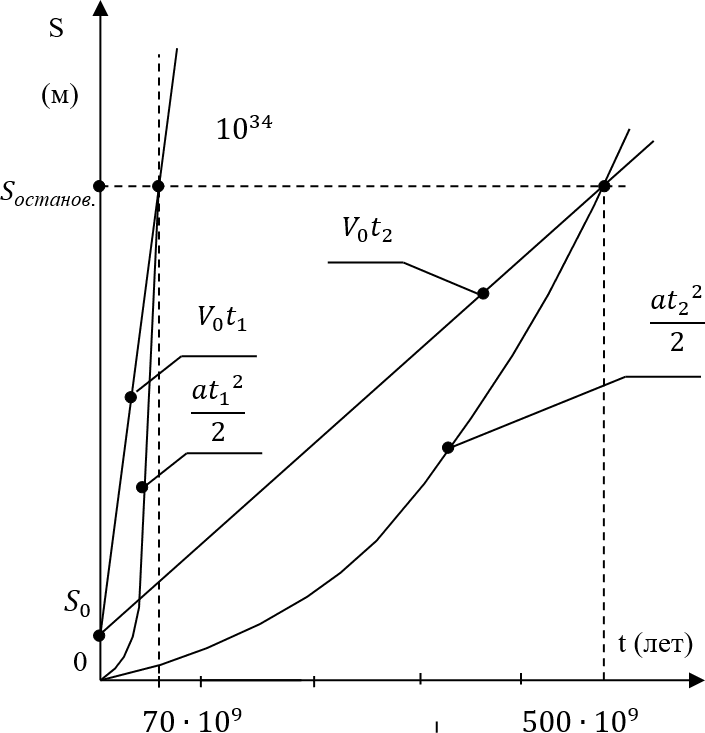
Рис. 20.6

Рисунок 20.6 иллюстрирует эти два примера. Здесь

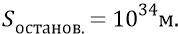
Однако у Большой Вселенной конечный размер стадии замедления вполне может оказаться величиной, допустим,

м или

м. Нам это сейчас никак неведомо. И поэтому в данной главе мы лишь иллюстрируем возможные количественные исходы развития Вселенной. Однако от самой философии этого её развития мы отходить не только не собираемся, но на оставшихся страницах главы попробуем, насколько сможем, уточнить: как пространственные параметры Вселенной, так и возможную форму (картинку – вид), какую может принять Большая Вселенная. Но уже сейчас нам абсолютно ясно, что физикам от их чисто «энергетической» модели Вселенной до нашей («в картинках») – ещё шагать и шагать.

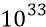
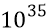
Но теперь нам надо, хотя бы каким-то способом, подтвердить факт – сначала останова электромагнитного вещества Скорлупы Вселенной, под действием, в основном, сил «поверхностного натяжения» Скорлупы, а затем – подтвердить неизбежную перспективу «падения» масс этого вещества на общую для этих масс «точку» Большого Взрыва. То есть надо подтвердить неизбежную перспективу сначала самой первой, а затем и гигантского множества последующих пульсаций родившейся электромагнитной Вселенной. Оперировать будем только простейшей классикой, с применением ньютоновых сил.

Для радиального останова Метагалактики в максимальной «точке» по высоте её зависания над Центром Взрыва, мы будем сравнивать между собой две силы:

1) силу инерции, под действием которой Метагалактика двигалась от Центра, имея массу М и ускорение а,

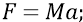
2) центростремительную силу, которая по своей физике представляет собой «силу поверхностного натяжения», направленную к Центру Взрыва.

Здесь ускорение движения Метагалактики по инерции нам уже известно и равно

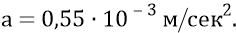
Займёмся теперь вычислением массы Метагалактики. Причём объём Метагалактики мы уже оценили величиной

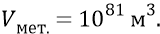
Поскольку плотность эфира определяется в нашей философии плотностью распределения низкочастотного слоя квантов этого эфира, служащего атомно-образующим слоем-уровнем, то определим эту плотность из условия, необходимого для поддержания в норме атомного резонанса. Для этого используем следующие характеристики:

1. Диаметр первой атомной орбиты составляет величину:

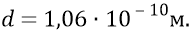
2. Частота собственных вращений электрона на первой боровской орбите – 2,16

при частоте обращения электрона по этой орбите –

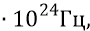
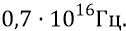
3. Частота излучения протоном ядра атома квантов его положительного поля:

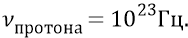
Именно это поле, следующее по направлению на электрон с такой частотой, является причиной того, что под действием его квантов электрон переходит каждый раз на новую хорду. Из сравнения собственных частот орбитального электрона и поля протона следует, что, двигаясь по хорде, электрон делает порядка 20-ти оборотов вокруг оси своей конструкции, подставляясь, следовательно, 20 раз плоскостью своей поляризации под поток квантов поля протона. И поскольку мы, уже наученные многочисленными примерами по поводу того, что Природа при строительстве своих любых объектов старается следовать по пути минимальных затрат, можем вполне предположить, что в течение этих 20-ти оборотов электрона, как бы находящегося при этом на орбите «в режиме ожидания», его орбиту может пересекать только один квант, который и переведёт его на новую хорду.

Тогда количество хорд электрона первой орбиты:

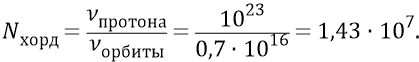
Но скорость кванта превышает скорость орбитального электрона в 137 раз. Это значит, что пока электрон пройдёт по хорде свой единичный прямолинейный путь на орбите

квант поля протона пролетит по радиус – лучу путь

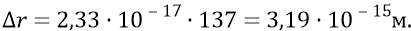
А это, в свою очередь, означает, что в любой момент времени «сейчас» на радиус – луче поля протона всегда должна двигаться цепочка последовательных квантов в количестве

Следовательно, минимальное количество квантов, которое было бы необходимым для того, чтобы удерживать электрон на первой атомной орбите и находящихся в момент «сейчас» внутри окружности орбиты, должно быть следующим:

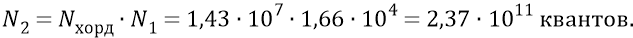
«Рисунок» распределения этих квантов внутри объёма (плоскости) орбиты будет подобен некоторой многовитковой спирали, раскручивающейся от протона, который будет, быстро вращаясь, как бы «разбрызгивать» от себя по трассе-нитке этой многовитковой спирали кванты своего поля, постепенно затем, виток за витком, пересекающих орбиту электрона в самых разных азимутах этой орбиты.

Итак, мы оценили общее количество квантов эфира, находящихся в любой данный момент времени внутри атомной орбиты (первой боровской), движущихся строго в плоскости этой орбиты. Однако, если поляризация этой орбиты и, следовательно, этих квантов будет вертикальной, то вертикальный круг – кольцо орбиты может располагаться вокруг своего вертикального диаметра (совпадающего, допустим, с осью z стандартной декартовой системы xyz) с любыми азимутами.

При определении же угла сдвига каждой плоскости, для получения всех возможных направлений полёта квантов эфира, мы находимся в состоянии серьёзной неопределённости. Но здесь достаточно точным условием приближения выберем то, в соответствии с которым распределение квантов, прошивающих атомную сферу, надо считать равномерным по всей площади сферы. А это значит, что на уровне сферы шаг следования квантов в азимутальном направлении для каждого данного угла места должен быть равен уже определённому нами шагу, равному единичной хорде для каждой вертикальной плоскости орбиты.

Однако одновременно с этим мы должны ввести некий поправочный коэффициент, учитывающий тот факт, что при каком-то данном азимутальном шаге, установленном по «экватору» получающейся сферы вращения, шаг на «северном» и «южном» полюсах сферы сокращается, увеличивая, следовательно, там плотность точек пересечения радиус-лучами поверхности сферы, а следовательно, увеличивая плотность квантов внутри сферы. Поэтому, для выравнивания общей плотности точек пересечения радиус-лучами поверхности сферы уменьшим количество квантов в объёме сферы, сократив количество азимутов. Тогда количество квантов, равномерно распределённых по объёму сферы, будет следующим:

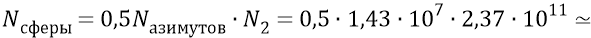
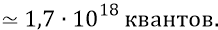
Но теперь в наши оценочные расчёты придётся внести ещё одну существенную поправку, касающуюся количества азимутов в сфере. Уже сейчас число азимутов равно:

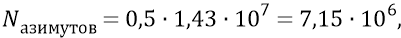
что приводит к угловому шагу азимутов,

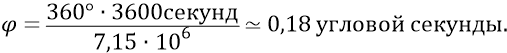
Далее рассуждаем следующим образом. При изначальном определении конкретных цифр числа хорд и количества импульсов-квантов привязки, распределённых по вертикальной плоскости поляризации атомной орбиты, мы исходили из энергии нуклона и из скоростей: кварков в нуклоне и электрона на орбите. А также мы исходили из условий атомного резонанса, главными из которых явились размеры атомной орбиты и длина волны кванта эфира низкочастотного слоя-уровня электромагнитного вакуума. То есть те кванты привязки, которые указаны в наших расчётах, это реальные кванты поля протона, собранные – направленные протоном из хаотических квантов эфира, налетающих на атом со всех сторон пространства эфира Метагалактики. И поскольку в нашем условии распределения азимутальных дискретов мы привязываемся к реальным квантам вертикальных сечений атомной сферы, собранным-направленным из окружающего эфира, то точно таким же образом мы должны относиться и к квантам, собираемым атомом из направлений азимутальных дискретов атомного объёма. То есть те кванты тех шагов-дискретов, которые «чертят» нам каждый следующий меридиан сферы, уже строго направлены конструкцией протона по «узким» вертикальным меридианам из первоначально «широких» азимутальных направлений действительно хаотического эфира. Почему первичные хаотически распределённые кванты эфира надо считать жёстко собранными в направленные «струнки» – линии квантов поля протона? Потому что эти внешние кванты, налетая на атом в направлениях, примерно совпадающих с плоскостью поляризации ядра-протона, проходят через конструкцию эфирки протона, дважды направляемые кварками этой конструкции. Сначала каждый такой внешний квант налетает на первый для него кварк конструкции эфирки, а затем, уже предварительно усилившись – направившись этой конструкцией первого кварка, квант прошивает второй кварк этой же конструкции, противоположной в ней первому кварку. Дважды направленный таким образом квант далее следует в жёстком направлении плоскости поляризации эфирки нуклона-протона, являясь уже именно тем «квантом привязки» электрона к протону, который будет теперь жёстко вписан в линию «тонкого» меридиана – как пересечения квантов поля эфирки с атомной сферой по линии – окружности меридиана.

То есть на самом деле хаотические кванты эфира, занимающие в пространстве такой же объём, какой занимает атомная сфера, не собраны в нашу линию-меридиан, но «распушены» в своём объёме. И поэтому мы вполне можем считать, что в реальном эфирном (не атомном) объёме, равном объёму атомной сферы, кванты, налетая на объём пространства, такой же, какой занимает в этой сфере реальный протон, далее будут следовать не с нашим «узко-направленным» азимутальным шагом, но с широким шагом, «распушенным» по крайней мере на два порядка величины по отношению к нашему азимутальному дискрету-шагу.