 полная версия
полная версияМузыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.
А теперь пропустим нижние узлы. Нам, по законам обертонов струны и природного звукового ряда, можно двигаться только в одну сторону: выше, а значит – вправо. А нижние узлы – левые: движение влево, и… снова вправо.
Но мы всё-таки будем следить за этими нижними узлами, не будем терять их из виду. На всякий случай.
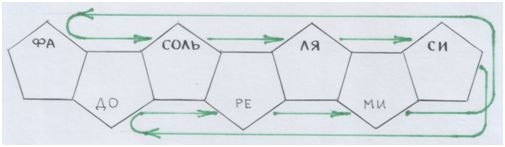
Рис. автора.
Можем продолжить эксперимент: перевернуть ленту из узлов. Нижние станут верхними.
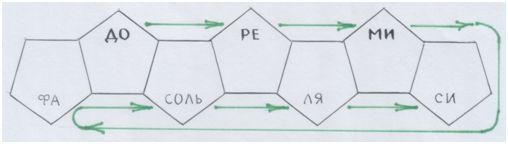
Рис. автора.
Потом можно опять перевернуть, и опять перевернуть.
Эти перевёртыши– повороты-вращения, похожие на перекрёсты и обратную пропорциональность, сотворят, наконец-то, привычный звукоряд:
ДО – РЕ – МИ – ФА – СОЛЬ – ЛЯ – СИ.
Диатоническая гамма.

(…перевернуть)

Рисунки автора.
Что будет, если продолжить ленту ?
Мы сможем это сделать, если совершим одну операцию: перевернём будущее продолжение ленты (такой же её отрезок, как предыдущий: удвоение!) на 180˚, – как это много веков спустя после Пифагора сделал со своей лентой Фердинанд Мёбиус.
Пифагор, безусловно, ничего не мог знать о Мёбиусе. Но он жил в пространстве всё тех же законов природы, что и Мёбиус. И мы живём всё там же. И экспериментируем.

Модель автора.
Эту ленту теперь спокойно можно замкнуть в кольцо. И путешествовать по двум поверхностям попеременно, как по одной, – но по обыкновенному кольцу.
Мёбиус наоборот?

Модель автора.
И ещё одно любопытное наблюдение: каждая нота/звук попеременно оказывается то в «фазе», то в «противофазе». Как волна.

Рис. автора.
(Лат. phasis – «появление», определённый момент в ходе развития какого-либо процесса.)
Давай вглядимся в процесс, который происходит в кольце с каждым звуком/тоном.
Каждый звук/тон через в о с е м ь шагов обретает своё повторение-совпадение, созвучие – к о н с о н а н с.
А лента-кольцо – сплошной «Мёбиус»: ведь каждый замкнутый узел (пентагон) обладает свойствами «Мёбиуса». Лента-кольцо из узлов замкнула все узлы разом.
Замкнутые в кольцо узлы-звуки произвели на свет о к т а в у: греч. «окто» – «восемь», лат. octava – «восьмая». Совершенный консонанс.
Один совершенный консонанс – квинта – произвёл на свет другой совершенный консонанс – октаву.
Если убрать пропущенные нижние левые узлы, то размашистая лента квинт сожмётся в д в о е. Как окружности в геометрической прогрессии!
(О, прости, вот в этом самом месте мою мысль просто-таки примагнитило к одной увлекательной идее. Через несколько страниц/листочков вернёмся к Пифагору.)
ЛИСТОЧКИ «МЫСЛЕЙ ВБОК» (о геометрической прогрессии).
(Следующие 9 страниц можно пропустить, а можно и полюбопытствовать…)
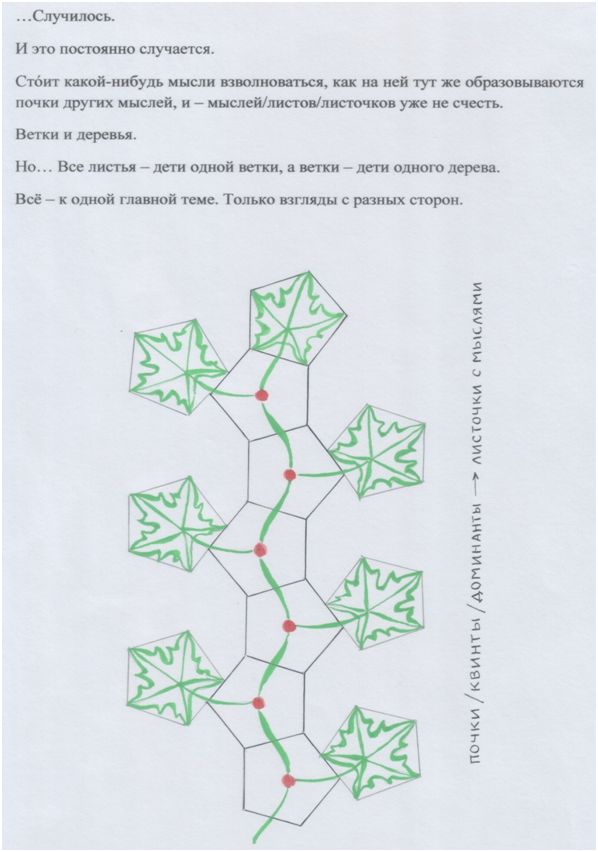
Рис. автора.
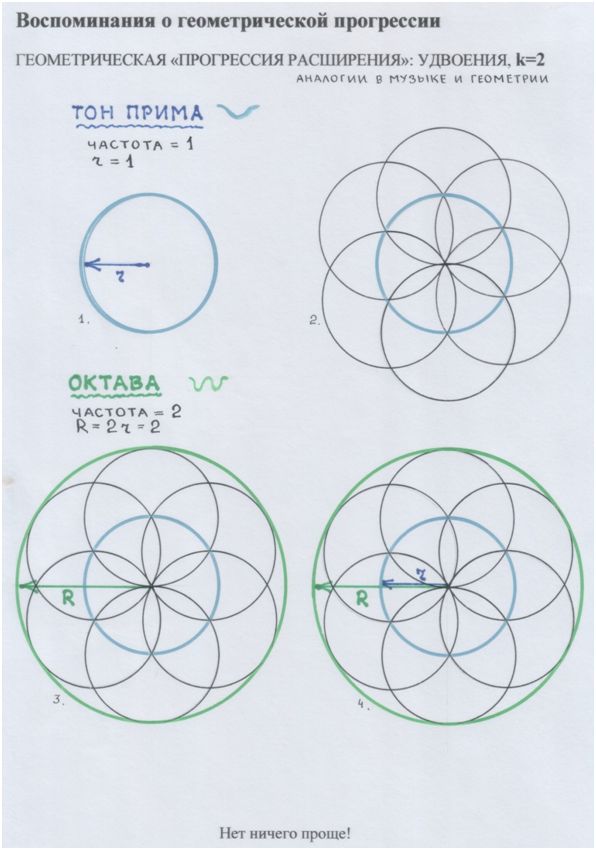
Рис. автора
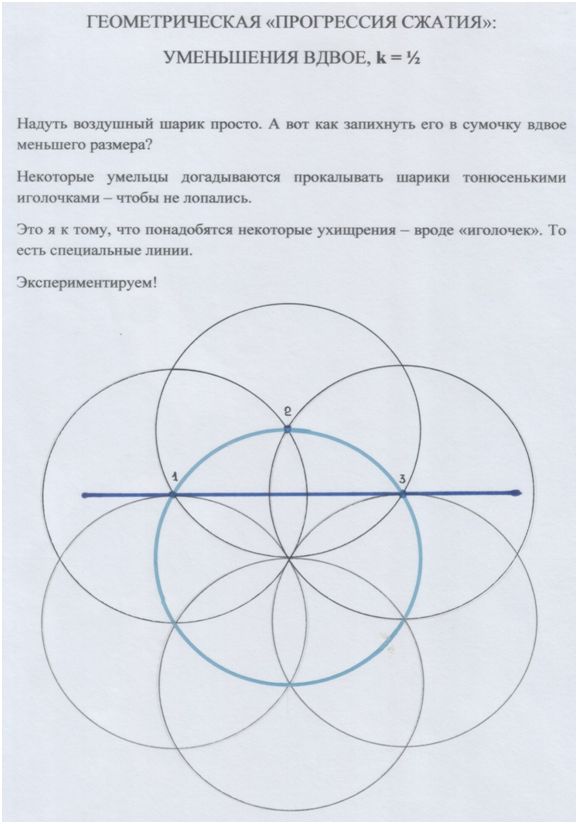
Рис. автора
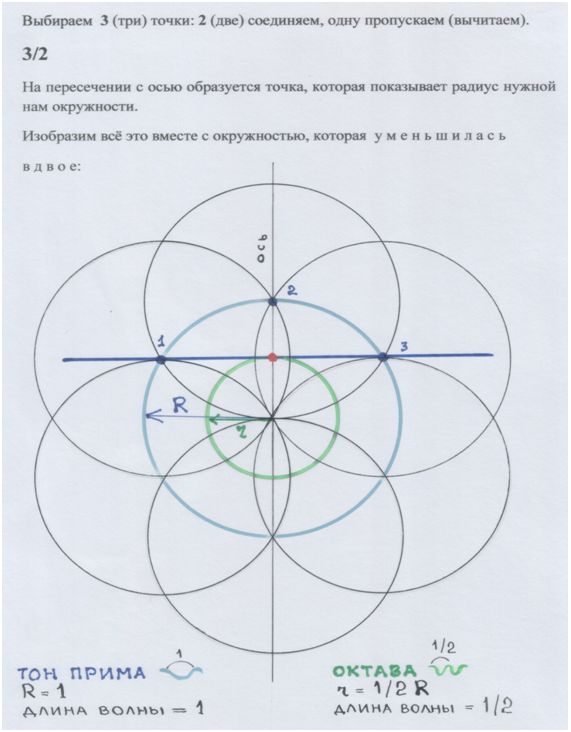
Рис. автора

Рис. автора

Рис. автора

Рис. и пометки автора.

Рис. и пометки автора.

Рис. и пометки автора.
Итак, Пифагору предстояло провести операцию сжатия размашистых квинт.
Этот п р о ц е с с ты буквально сможешь ощутить своими руками, если не поленишься сделать простенькую модель из узлов.
А что? Пифагор ведь тоже догадался незримое (звук) исследовать с помощью п р е д м е т а – струны.

Модель автора.
Растяни узлы в волну, а потом начни складывать «гармошкой».
…Ты ощущаешь, как узлы/квинты закручиваются в винт?
Теперь не очень плотно складывай, – так, чтобы видеть названия нот.
…Винтовая лестница!
Посмотри сбоку.
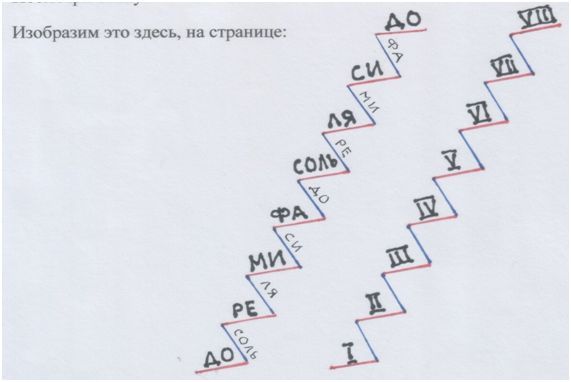
Рис. автора.
А теперь изобразим ступеньки этой лестницы под прямым углом:
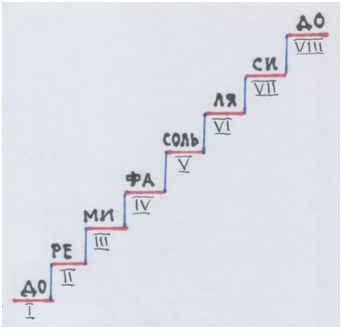
Рис. автора.
Нижние квинты спрятались совсем. Словно исчезли, как тени в полдень.
И мы теперь видим привычные нам ступени гаммы.
Как их обозначали древние греки? Как они называли сами звуки? – Мы пожимаем плечами.
Если верить историкам музыки, первые попытки записывать музыкальные звуки знаками, появились не раньше 11 века. И выглядели эти знаки как просто точки или квадратики на двух линейках. Названия этих звуков/знаков тоже появились в Средние века, через полтора с лишним тысячелетия после Пифагора.
А вот ступени могли обозначаться числами. А числа записывались буквами греческого алфавита. А древнегреческий алфавит уж наверняка отличался от нынешнего.
Вот поэтому удобнее иметь дело с геометрическими образами.
Геометрия сама всё показывает.
А пересказывать то, что показывает геометрия, мы будем на привычном нам языке. Так и поступают исследователи музыки. Они переводят древние знания на привычные нам языки с их знаками: буквы латинского (или русского) алфавита (вот! греческие названия нот даже не употребляются), арабские (индийские) и латинские цифры для обозначения чисел.
Для пифагорова музыкального строя имеют значение именно интервалы.
Сами характеристики отдельных звуков выражены как интервалы: то есть каждый звук определяется отношением к другому звуку (вот где корни относительности!). Первый взятый звук становится точкой отсчёта (точкой опоры). А все остальные звуки находятся по законам гармонии, консонансов:
Первый консонанс – ПРИМА ( двойной первый звук, унисон, сам себе консонанс: 1/1).
Второй консонанс – ОКТАВА (второй из двойного звука ПРИМЫ растянулся в диапазон-ОКТАВУ: 1-2, второй звук по отношению к первому, 2/1).
Третий консонанс – КВИНТА (третий звук по отношению ко второму : 3/2 ).
Четвёртый консонанс – КВАРТА (четвёртый звук по отношению к третьему : 4/3 и в то же время – это перевёрнутая квинта, отношение октавы к квинте; 2:3/2, или 2х2/3=4/3).
Таким образом, каждому звуку присваивается своя дробь, – которая, собственно и является знаком о т н о ш е н и я.
То есть, в каждом звуке уже спрятан интервал ( интервал/расстояние/отрезок струны/волны или отрезок «пробега» волны по частотам, как в нашей ленте частот).
И, получается, только в Средние века этим дробям/отношениям дали буквенные (или слоговые) названия, которыми мы и пользуемся:
1/1, прима – ДО1.
2/1, октава – ДО2.
3/2, квинта – СОЛЬ.
4/3, кварта – ФА
Если интересно, найди в Интернете статью «Как появились названия нот?».
Пифагор оперировал только числами.
Он поклонялся Числу, словно божеству.
Все вещи мира, все явления можно выразить Числом! – вот главная идея его вдохновенного мышления.
Все названия звуков, которые он находил, происходят от чисел. И названия интервалов – от чисел.
Мы, конечно, будем пользоваться именами звуков для лучшего понимания, но всегда будем иметь в виду, что за этими именами – числа.
Вот и наша лестница квинт пронумерована числами-ступенями.
Головокружительно вот что:
Получается, что каждый звук этой лестницы – этакая микроквинта.
Хотя, в общем-то, ничего особенно удивительного в этом и нет, если вспомнить, что у квинты – функция (роль) д о м и н а н т ы – высшего напряжения, высшего проявления какого-то качества, характера. В нашем случае – максимум проявления характера каждого звука, его особенности.
Дух захватывает только когда осознаёшь, что на пятой ступени лестницы мощность отдельного звука-микроквинты (соль) словно пятикратно возрастает: квинта, да ещё и в положении КВИНТЫ в октаве! Квинта обретает новый масштаб! Она п о д о б н а себе, но уже в ином масштабе.
Этот процесс можно увидеть страничкой ниже.
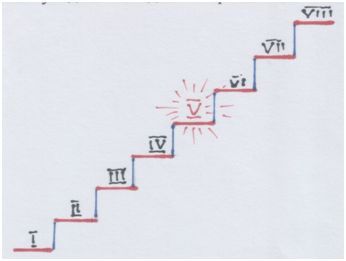



Рисунки и модели автора.
А что же остальные звуки?
Сохранились ли в них хотя бы намёки на их «первородство» – на квинту?
Давай посмотрим на одну таблицу. Она показывает следующий этап процесса сотворения музыкального строя Пифагором: вычисленные им остальные звуки октавы.
Для удобства понимания на ней указаны имена звуков, но за каждым из них – Число! (по-«пифагоровски»). /ниже – таблица из книги: Волошинов М.В. «Математика и искусство»/
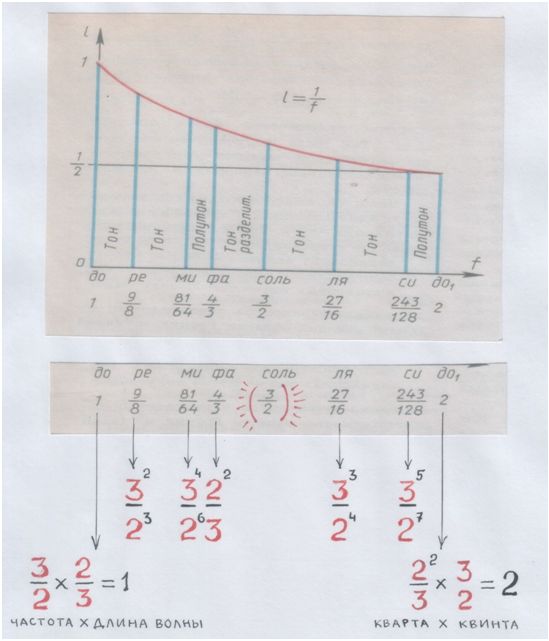
Рис. и пометки автора.
Да, как-то хитро запрятались квинты внутрь других звуков. И не распознаешь их с первого взгляда.
Кстати, ты заметил, что все числа – это частоты: числитель дробей больше знаменателя, «большее на меньшее», большее число в отношении к меньшему. У длин волн – наоборот: меньшее число в отношении к большему. Надеюсь, ты помнишь про этот перевёртыш/перекрёст.
Да и сам первый звук (прима) уже словно намекает на то, что предстоит увлекательная игра в перевёртыши: если частоту звука умножить на длину его волны, то и получится е д и н и ц а, начало отсчёта.

А если частоту квинты умножить на частоту её перевёртыша – частоту кварты, – получится октава (по частоте). Или перемножить длины волн квинты и её перевёртыша кварты, – будет октава по длине волны. Этакий расширенный, удвоенный перевёртыш.

Да и сама октава – удвоенная единица-прима: 2. Или поделённая пополам: ½.
( Опять – геометрическая прогрессия?!)
Прима – нижняя граница звукоряда. Октава – верхняя граница.
В середине – квинта и её перевёртыш кварта.
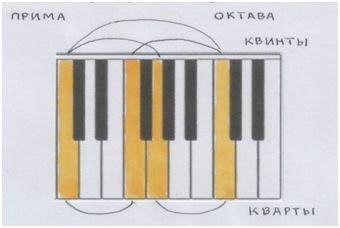
Рис. автора.
Да, по-видимому, Пифагор понял, что отношения между этими звуками и интервалы, которые образуются из их отношений, и должны стать ключом к поиску характеристик других звуков – их частот и длин волн.
Давай-ка ещё разочек обратимся к ленте частот.
О, этот долгий путь ко всеобщему консонансу и гармонии!
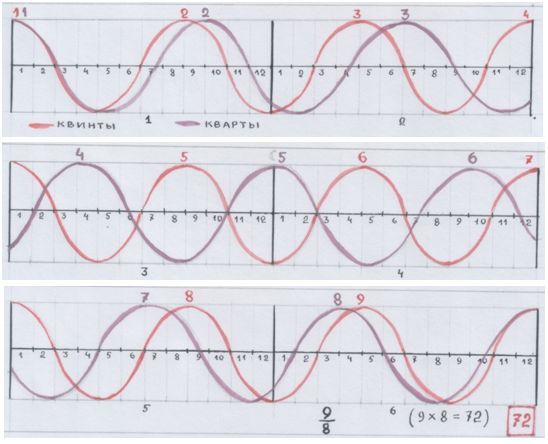
Рис. автора.
Путь получился долгим из-за того, что квинте пришлось вращаться-обращаться в кварту, и это вращение-обращение должно было прийти к консонансу в конце концов.
Отношения частот прямой квинты и её обращения кварты произвело на свет новое отношение и новый звук: 9/8.
9/8. Девять кульминаций квинты к восьми кульминациям кварты.
В таблице – это звук РЕ. II ступень.

Рис. автора.
То же самое отношение получится, если перевернуть кварту и умножить этот перевёртыш на квинту. (Перевёртыш перевёртыша – просто голова крýгом!)

Рис. автора.
Если результат этой операции умножить на результат такой же операции (результат в квадрате), то есть 9/8 х 9/8, получим следующий звук.
9/8 х 9/8 = 81/64
Получилась частота МИ. III ступень.
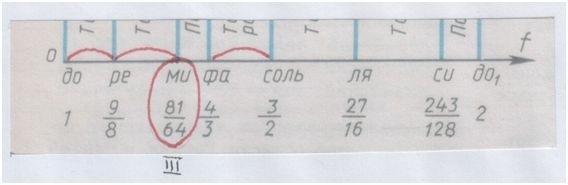
Рис. автора.
Следующая ступень, IV, нам известна: кварта, 4/3.
Умножим 81/64 (ми) на 4/3 (фа): 81/64 х 4/3 = 27/16.
Это частота ЛЯ, VI ступень.
Её же можно получить, «воспользовавшись услугами» известной нам Vступени, квинты: умножить квинту 3/2 на тон 9/8. 3/2 х 9/8 = 27/16.
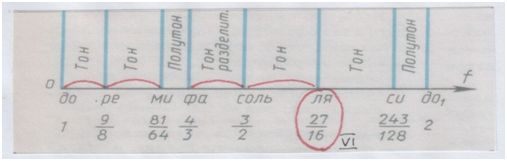
Рис. автора.
VII-ю ступень, СИ, мы получим, умножив частоту ЛЯ опять же на тон 9/8:
27/16 х 9/8 = 243/128

Рис. автора.
Между прочим, если мы и кварту 4/3 умножим на тон 9/8, то получим квинту: 4/3 х 9/8 = 3/2
…И все эти числа – реально звучат!
… А ты заметил, что ТОН/звук у нас теперь фигурирует и в качестве
р а с с т о я н и я между звуками?
Удивительно: ТОН – и сам звук, и в то же время – расстояние между звуками в октаве!
Может, это – из-за в о л н ы?
Ведь звуковая волна «пробегает» р а с с т о я н и е.
Вспомни ленту частот. Волне примы пришлось «пробежать» шесть своих расстояний, пока не свершился Великий Консонанс: созвучие примы, октавы, квинты и кварты.
А ведь прима – ТОН, с которого всё начинается, чтобы прийти к октаве. А шесть «пробежек» приме пришлось совершить из-за отношений квинты и кварты (перевёртыша квинты).
Вот так всё и сошлось: в октаве должно быть шесть тонов, а каждый тон выражает отношение между квинтой и квартой: девять кульминаций квинты к восьми кульминациям кварты – 9/8.
Да может быть, и сама октава (от греч. «окто» – «восемь») получила такое название из-за этих самых восьми кульминаций кварт!
Кварта (то есть квинта наоборот) «виновата»!
И даже отношение октавы (восемь её ступеней) к шести тонам указывает на эту «виновницу»! 8/6 = 4/3
…Вернёмся, однако, к сотворению октавы. Ещё не всё завершено в ней.
Тонов должно быть ш е с т ь, а у нас набирается пока что целых тонов всего пять:
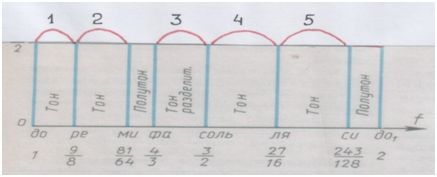
Рис. автора.
Заметим попутно: тон между ФА и СОЛЬ назван р а з д е л и т е л ь н ы м.
Почему? А посмотри:
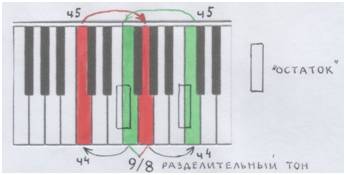
Рис. автора.
Вспомнил эту картинку? Квинта снизу вверх в октаве и её перевёртыш сверху вниз и образуют этот самый разделительный тон. И разделяют октаву на две кварты: ДО1-ФА и СОЛЬ-ДО2. Они одинаковы. И в каждой – по два целых тона и «остаток». Тоже одинаковый.
Существует несколько способов его вычислить.
Давай попробуем это сделать, исходя из той простой мысли, что «остаток» предполагает деление.
Итак, в кварте ДО1-ФА частоту ФА разделим на частоту соседнего МИ:
4/3:81/64 = 4/3х64/81 = 256/243
В кварте СОЛЬ-ДО2 частоту ДО2 разделим на частоту соседнего СИ:
2:243/128 = 2х128/243 = 256/243
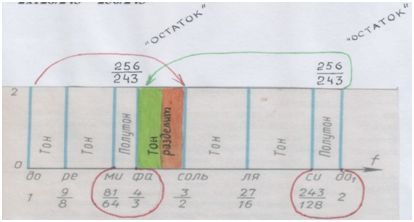
Рис. автора.
Таблица, которую ты увидишь сейчас, – совершенно замечательная таблица!
Что в ней стóит заметить?
С одной стороны, она похожа на таблицу предыдущую.
А вот с другой стороны… Взгляд с другой стороны – это тот же перевёртыш. Мысленный перевёртыш.
И в самой таблице мы увидим перевёртыш: сами звуки показаны как частоты, а расстояния между звуками – как длины.
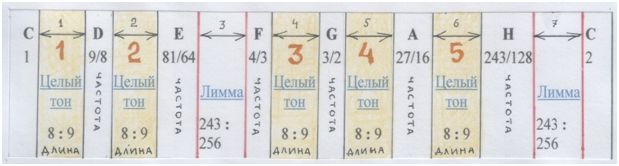
Рис. автора.
Обрати внимание на РЕ (D). Под самим звуком указана его частота. А расстояние от РЕ (D) до примы ДО (С) – как д л и н а в о л н ы РЕ. Выходит, наша гипотеза о происхождении расстояний между звуками из-за того, что волны обладают длиной (или периодом), имеет всё-таки основание.
И главной мерой расстояний между звуками стал ТОН.
Давай-ка ещё разочек заберёмся внутрь этого самого ТОНА, вглядимся в него:
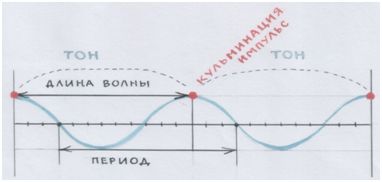
Рис. автора.
То что мы называли «кульминацией» на музыкальном языке, на языке физики «импульс».
Энциклопедия:
Импульс: от лат. impulsus – «удар», «толчок»; всплеск, усилие, побуждение.
Звуковой импульс – внезапно и быстро исчезающее повышение давления.
Изменение напряжения.
Усилие, напряжение – ведь это же главные свойства д о м и н а н т ы! И главные характеристики к у л ь м и н а ц и и.
А в физике – и м п у л ь с.
На языке физики мы бы сказали, что волна п р и м ы имеет ш е с т ь импульсов (если посмотрим на нашу полосу частот); волна о к т а в ы имеет д в е н а д ц а т ь импульсов; волна к в и н т ы имеет д е в я т ь импульсов; волна к в а р т ы имеет в о с е м ь импульсов. И все они словно борются друг с другом, то соединяясь, то противостоя, усиливая и погашая усилия друг друга, – пока не придут ко всеобщему согласию через какой-то диапазон/расстояние. И тогда все их усилия соединяются в согласии.
Физики бы сказали, что в этом моменте наступает резонанс.
Латинское слово resono – «откликаюсь»; resonans – «отзвук» (sono – звук, re – поворот).
Вот! В диапазоне октавы после согласия-резонанса наступает поворот-отражение. Октава – словно зеркало, в котором квинта отражается в кварту! И все остальные звуки отражаются в обратном порядке. Повороты-перевёртыши. И… с и м м е т р и я: левое – отражение правого, правое – левого. И так – опять до примы, пока не замкнётся кольцо. И всё повторится снова.
Все интервалы в октаве – симметрично отражаются:
Октава – отражение примы; септима – отражение секунды; секста – отражение терции.
Кварта – отражение квинты. Но… со смещением от центра симметрии!
Если бы квинта отразилась строго в центре симметрии, получились бы два
д и с с о н и р у ю щ и х, два самых сверхнапряжённых интервала, тех самых, которые называют «волчьими квинтами» (увеличенная кварта, или уменьшённая квинта). И тогда всю музыку пришлось бы промерять этими «воющими» интервалами! Всю – начиная с диатоники. Представляешь, вся музыка превратилась бы в вой! И вместо гармонии – хаос!
Квинта должна была сохранить свою чистоту – остаться чистой квинтой.
И отразиться чистой квартой.
Это возможно только в том случае, если и расстояния между звуками будут подобны квинте.
И в самом деле, взгляни на знакомую таблицу, – и ты увидишь, что звуки с их высчитанными частотами словно сами собой распределились по расстояниям в соответствии с квинтой: два тона – три тона. 2/3. По длине волны квинты.
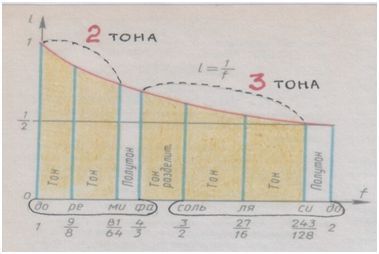
Рис. автора.
А оставшийся ш е с т о й тон стал границей, разделом, – сам поделившись надвое.
Сами звуки расположились симметрично, по квартам. А расстояния между ними – асимметрично, по квинтам.
Симметрия и асимметрия – в одном.
Симметрия и асимметрия в одной октаве.
Симметрия и асимметрия в отрезке (октава – интервал, интервал – отрезок).
Быть может, ты вспомнишь, где нам встречалось это явление: сочетание симметрии и асимметрии вместе?
… «ДЕЛЕНИЕ ОТРЕЗКА В КРАЙНЕМ И СРЕДНЕМ ОТНОШЕНИИ»…
…Ну, конечно же… Золотое сечение!
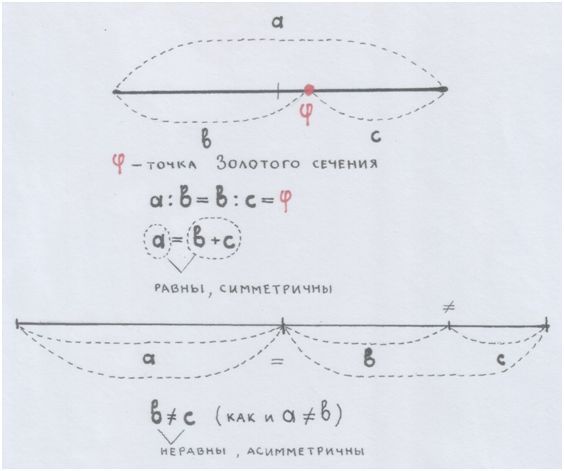
Рис. автора.
Но вместе всё это сотворяет особую симметрию – САМОПОДОБИЕ.
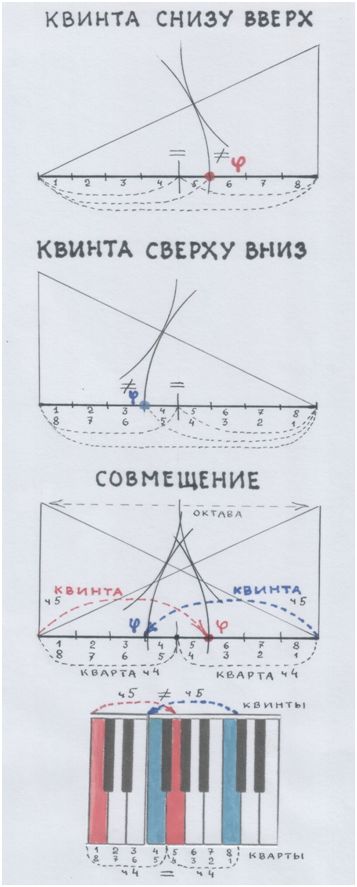
Рис. автора
Геометрические мысли о консонансах.

Модель автора

Рис. и пометки автора.
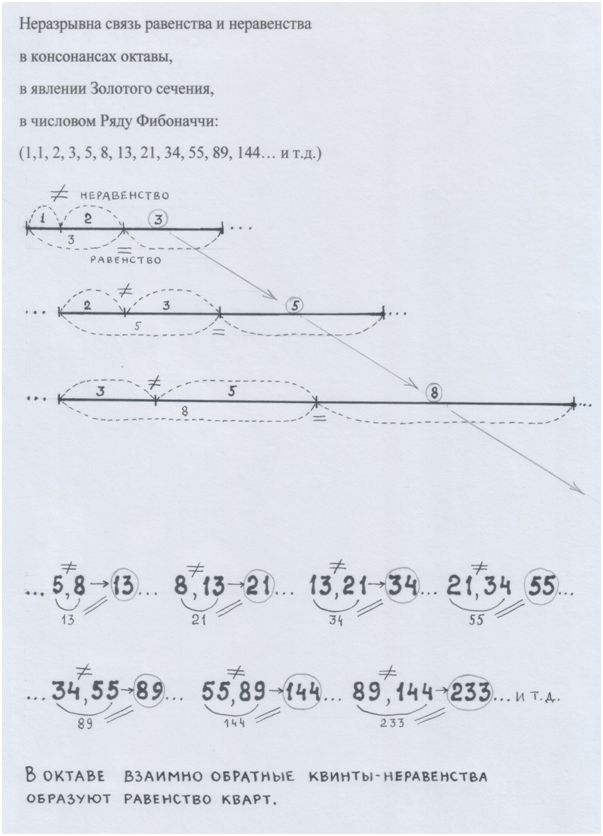
Рис. и пометки автора.
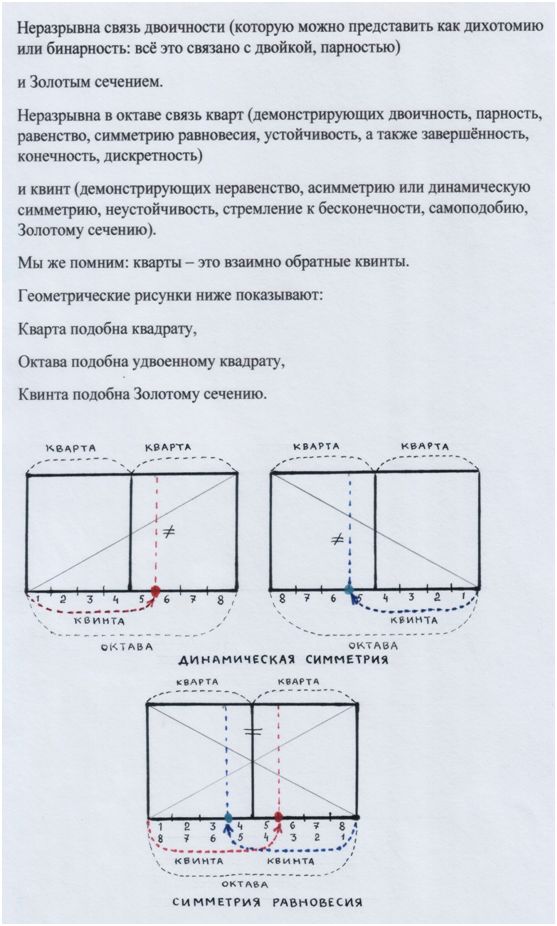
Рис. и пометки автора.
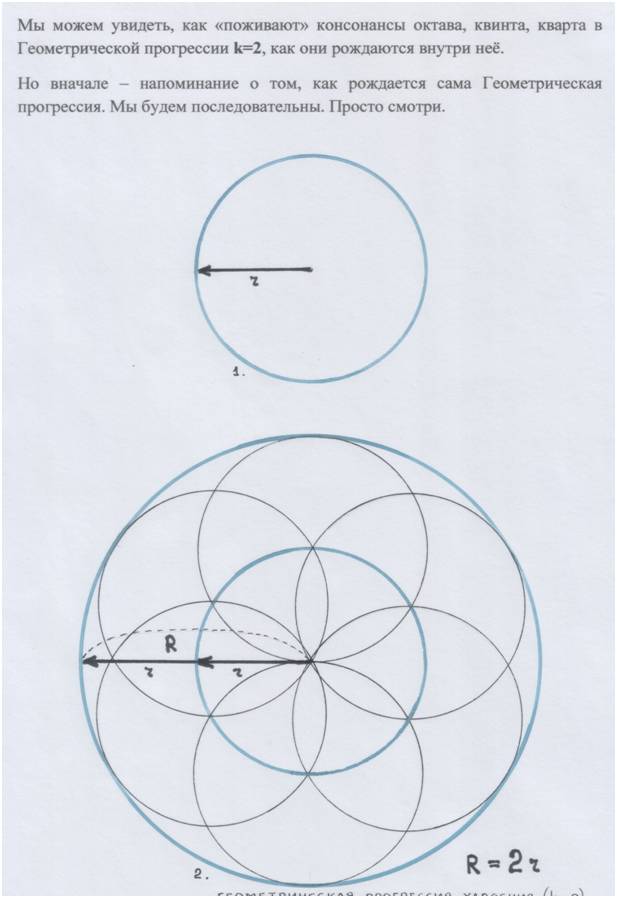
Рис. и пометки автора.
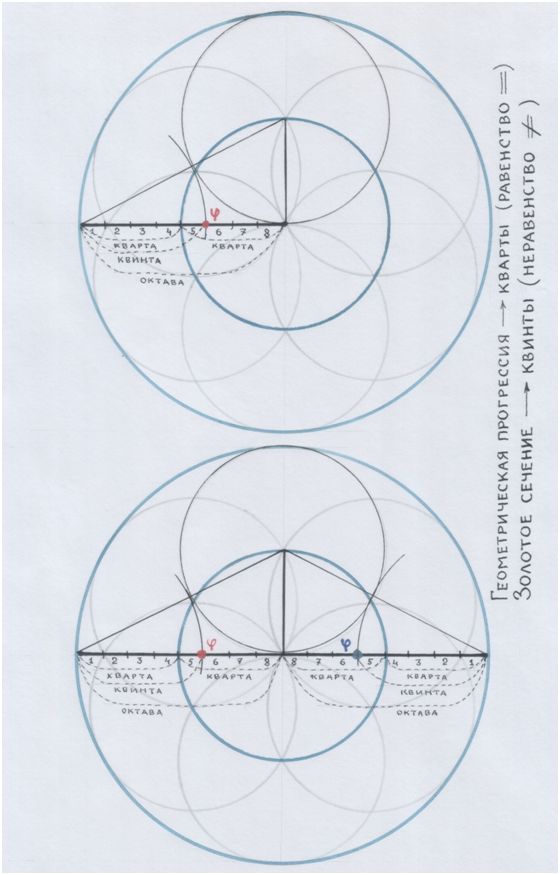
Рис. и пометки автора.
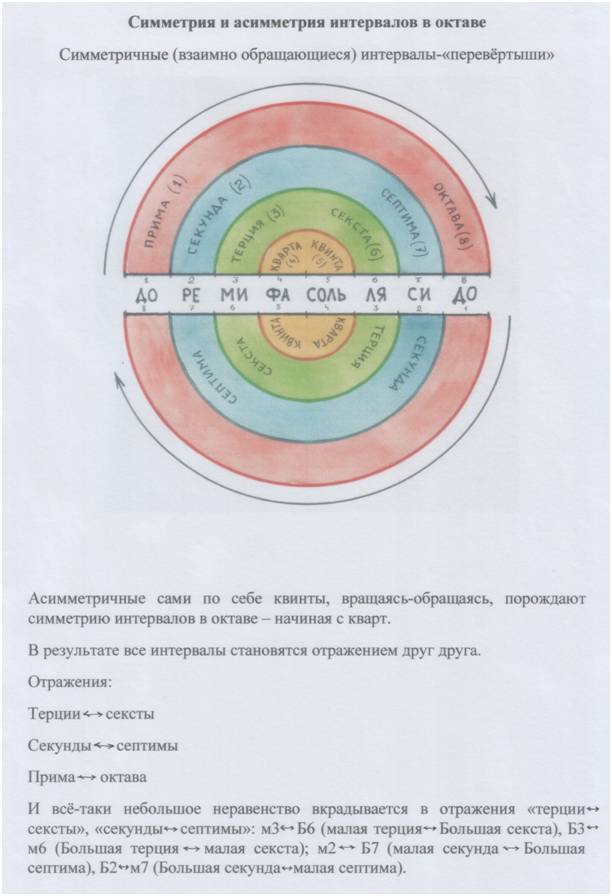
Рис. и пометки автора.
…Ох, это Золотое сечение! Куда ни взглянешь – машет ручкой: привет-привет! А уж на клавишах так прямо само в глаза бросается: вот оно я! Вот же!
Как же Пифагор обходился без клавиш?
Ну не было их тогда. Вместо клавиш – геометрия! Отрезки, пропорции, числа-дроби.
Вот и та, последняя, таблица, с интервалами-отрезками между звуками октавы… Мы в ней далеко не всё интересное разглядели и обмыслили.
Слово там одно необычное не даёт покоя.
Ты видишь его, это слово?

Рис. автора.
…ЛИММА.
Зачем здесь такое странное слово?
Странное. Но какое красивое!
Греческое.
А означает – «остаток». Всего лишь! Так просто…
Однако греки и любили-то именно сочетание простоты и красоты.
Ну сравни сам, вслушайся: «полутон» и … Лимма, Леймма… Это же музыка!
Даже в простом слове – музыка.

