The Way To Geometry

The other, to witt the learned Snellius, in his Eratosthenes Batavus, a booke which hee hath written of the true quantity of the compasse of the Earth, describeth many more, and that after a farre more exact and curious manner.

Here observe, that besides those by us here set downe, there are certaine others by him mentioned, which as hee writeth are found wholly to agree with some one or other of these. For Rheinlandicus, that of Rheinland or Leiden, which hee maketh his base, is all one with Romanus, the Italian or Roman foote. Lovaniensis, that of Lovane, with that of Antwerpe: Bremensis, that of Breme in Germany, with that of Hafnia, in Denmarke. Onely his Pes Arabicus, the Arabian foote, or that mentioned in Abulfada, and Nubiensis: the Geographers I have overpassed, because hee dareth not, for certeine, affirme what it was.

Looke of what parts Pes Tolitanus, the spanish foote, or that of Toledo in Spaine, conteineth 120. of such is the Pes.

Heidelbergicus, that of Heidelberg, 137.

Hetruscus, that of Tuscan, in Italie, 138.

Sedanensis, of Sedan in France, 139.

Romanus, that of Rome in Italy, 144.

Atticus, of Athens in Greece, 150.

Anglicus, of England, 152.

Parisinus, of Paris in France, 160.

Syriacus, of Syria, 166.

Ægyptiacus, of Egypt, 171.

Hebraicus, that of Iudæa, 180.

Babylonius, that of Babylon, 200.

Looke of what parts Pes Romanus, the foote of Rome, (which is all one with the foote of Rheinland) is 1000. of such parts is the foote of

Toledo, in Spaine, 864.

Mechlin, in Brabant, 890.

Strausburgh, in Germany, 891.

Amsterdam, in Holland, 904.

Antwerpe, in Brabant, 909.

Bavaria, in Germany, 924.

Coppen-haun, in Denmarke, 934.

Goes, in Zeland, 954.

Middleburge, in Zeland, 960.

London, in England, 968.

Noremberge, in Germany, 974.

Ziriczee, in Zeland, 980.

The ancient Greeke, 1042.

Dort, in Holland, 1050.

Paris, in France, 1055.

Briel, in Holland, 1060.

Venice, in Italy, 1101.

Babylon, in Chaldæa, 1172.

Alexandria, in Egypt, 1200.

Antioch, in Syria, 1360.

Of all other therefore our English foote commeth neerest unto that used by the Greekes: And the learned Master Ro. Hues, was not much amisse, who in his booke or Treatise De Globis, thus writeth of it Pedem nostrum Angli cum Græcorum pedi æqualem invenimus, comparatione facta cum Græcorum pede, quem Agricola & alij ex antiquis monumentis tradiderunt.

Now by any one of these knowne and compared with ours, to all English men well knowne the rest may easily be proportioned out.

2. The thing proposed to bee measured is a Magnitude.

Magnitudo, a Magnitude or Bignesse is the subject about which Geometry is busied. For every Art hath a proper subject about which it doth employ al his rules and precepts: And by this especially they doe differ one from another. So the subject of Grammar was speech; of Logicke, reason; of Arithmeticke, numbers; and so now of Geometry it is a magnitude, all whose kindes, differences and affections, are hereafter to be declared.

3. A Magnitude is a continuall quantity.

A Magnitude is quantitas continua, a continued, or continuall quantity. A number is quantitas discreta, a disjoined quantity: As one, two, three, foure; doe consist of one, two, three, foure unities, which are disjoyned and severed parts: whereas the parts of a Line, Surface, and Body are contained and continued without any manner of disjunction, separation, or distinction at all, as by and by shall better and more plainely appeare. Therefore a Magnitude is here understood to be that whereby every thing to be measured is said to bee great: As a Line from hence is said to be long, a Surface broade, a Body solid: Wherefore Length, Breadth, and solidity are Magnitudes.

4. That is continuum, continuall, whose parts are contained or held together by some common bound.

This definition of it selfe is somewhat obscure, and to be understand onely in a geometricall sense: And it dependeth especially of the common bounde. For the parts (which here are so called) are nothing in the whole, but in a potentia or powre: Neither indeede may the whole magnitude bee conceived, but as it is compact of his parts, which notwithstanding wee may in all places assume or take as conteined and continued with a common bound, which Aristotle nameth a Common limit; but Euclide a Common section, as in a line, is a Point, in a surface, a Line: in a body, a Surface.

5. A bound is the outmost of a Magnitude.

Terminus, a Terme, or Bound is here understood to bee that which doth either bound, limite, or end actu, in deede; as in the beginning and end of a magnitude: Or potentia, in powre or ability, as when it is the common bound of the continuall magnitude. Neither is the Bound a parte of the bounded magnitude: For the thing bounding is one thing, and the thing bounded is another: For the Bound is one distance, dimension, or degree, inferiour to the thing bounded: A Point is the bound of a line, and it is lesse then a line by one degree, because it cannot bee divided, which a line may. A Line is the bound of a surface, and it is also lesse then a surface by one distance or dimension, because it is only length, wheras a surface hath both length and breadth. A Surface is the bound of a body, and it is lesse likewise then it is by one dimension, because it is onely length and breadth, whereas as a body hath both length, breadth, and thickenesse.

Now every Magnitude actu, in deede, is terminate, bounded and finite, yet the geometer doth desire some time to have an infinite line granted him, but no otherwise infinite or farther to bee drawane out then may serve his turne.

6. A Magnitude is both infinitely made, and continued, and cut or divided by those things wherewith it is bounded.

A line, a surface, and a body are made gemetrically by the motion of a point, line, and surface: Item, they are conteined, continued, and cut or divided by a point, line, and surface. But a Line is bounded by a point: a surface, by a line: And a Body by a surface, as afterward by their severall kindes shall be understood.

Now that all magnitudes are cut or divided by the same wherewith they are bounded, is conceived out of the definition of Continuum, e. 4. For if the common band to containe and couple together the parts of a Line, surface, & Body, be a Point, Line, and Surface, it must needes bee that a section or division shall be made by those common bandes: And that to bee dissolved which they did containe and knitt together.

7. A point is an undivisible signe in a magnitude.

A Point, as here it is defined, is not naturall and to bee perceived by sense; Because sense onely perceiveth that which is a body; And if there be any thing lesse then other to be perceived by sense, that is called a Point. Wherefore a Point is no Magnitude: But it is onely that which in a Magnitude is conceived and imagined to bee undivisible. And although it be voide of all bignesse or Magnitude, yet is it the beginning of all magnitudes, the beginning I meane potentiâ, in powre.

8. Magnitudes commensurable, are those which one and the same measure doth measure: Contrariwise, Magnitudes incommensurable are those, which the same measure cannot measure. 1, 2. d. X.

Magnitudes compared betweene themselves in respect of numbers have Symmetry or commensurability, and Reason or rationality: Of themselves, Congruity and Adscription. But the measure of a magnitude is onely by supposition, and at the discretion of the Geometer, to take as pleaseth him, whether an ynch, an hand breadth, foote, or any other thing whatsoever, for a measure. Therefore two magnitudes, the one a foote long, the other two foote long, are commensurable; because the magnitude of one foote doth measure them both, the first once, the second twice. But some magnitudes there are which have no common measure, as the Diagony of a quadrate and his side, 116. p. X. actu, in deede, are Asymmetra, incommensurable: And yet they are potentiâ, by power, symmetra, commensurable, to witt by their quadrates: For the quadrate of the diagony is double to the quadrate of the side.

9. Rationall Magnitudes are those whose reason may bee expressed by a number of the measure given. Contrariwise they are irrationalls. 5. d. X.

Ratio, Reason, Rate, or Rationality, what it is our Authour (and likewise Salignacus) have taught us in the first Chapter of the second booke of their Arithmetickes: Thither therefore I referre thee.

Data mensura, a Measure given or assigned, is of Euclide called Rhetè, that is spoken, (or which may be uttered) definite, certaine, to witt which may bee expressed by some number, which is no other then that, which as we said, was called mensura famosa, a knowne or famous measure.

Therefore Irrationall magnitudes, on the contrary, are understood to be such whose reason or rate may not bee expressed by a number or a measure assigned: As the side of the side of a quadrate of 20. foote unto a magnitude of two foote; of which kinde of magnitudes, thirteene sorts are mentioned in the tenth booke of Euclides Elements: such are the segments of a right line proportionally cutte, unto the whole line. The Diameter in a circle is rationall: But it is irrationall unto the side of an inscribed quinquangle: The Diagony of an Icosahedron and Dodecahedron is irrationall unto the side.

10. Congruall or agreeable magnitudes are those, whose parts beeing applyed or laid one upon another doe fill an equall place.

Symmetria, Symmetry or Commensurability and Rate were from numbers: The next affections of Magnitudes are altogether geometricall.

Congruentia, Congruency, Agreeablenesse is of two magnitudes, when the first parts of the one doe agree to the first parts of the other, the meane to the meane, the extreames or ends to the ends, and lastly the parts of the one, in all respects to the parts, of the other: so Lines are congruall or agreeable, when the bounding, points of the one, applyed to the bounding points of the other, and the whole lengths to the whole lengthes, doe occupie or fill the same place. So Surfaces doe agree, when the bounding lines, with the bounding lines: And the plots bounded, with the plots bounded doe occupie the same place. Now bodies if they do agree, they do seeme only to agree by their surfaces. And by this kind of congruency do we measure the bodies of all both liquid and dry things, to witt, by filling an equall place. Thus also doe the moniers judge the monies and coines to be equall, by the equall weight of the plates in filling up of an equall place. But here note, that there is nothing that is onely a line, or a surface onely, that is naturall and sensible to the touch, but whatsoever is naturall, and thus to be discerned is corporeall.

Therefore

11. Congruall or agreeable Magnitudes are equall. 8. ax. j.

A lesser right line may agree to a part of a greater, but to so much of it, it is equall, with how much it doth agree: Neither is that axiome reciprocall or to be converted: For neither in deede are Congruity and Equality reciprocall or convertible. For a Triangle may bee equall to a Parallelogramme, yet it cannot in all points agree to it: And so to a Circle there is sometimes sought an equall quadrate, although incongruall or not agreeing with it: Because those things which are of the like kinde doe onely agree.

12. Magnitudes are described betweene themselves, one with another, when the bounds of the one are bounded within the boundes of the other: That which is within, is called the inscript: and that which is without, the Circumscript.

Now followeth Adscription, whose kindes are Inscription and Circumscription; That is when one figure is written or made within another: This when it is written or made about another figure.

Homogenea, Homogenealls or figures of the same kinde onely betweene themselves rectitermina, or right bounded, are properly adscribed betweene themselves, and with a round. Notwithstanding, at the 15. booke of Euclides Elements Heterogenea, Heterogenealls or figures of divers kindes are also adscribed, to witt the five ordinate plaine bodies betweene themselves: And a right line is inscribed within a periphery and a triangle.

But the use of adscription of a rectilineall and circle, shall hereafter manifest singular and notable mysteries by the reason and meanes of adscripts; which adscription shall be the key whereby a way is opened unto that most excellent doctrine taught by the subtenses or inscripts of a circle as Ptolomey speakes, or Sines, as the latter writers call them.

The second Booke of Geometry. Of a Line

1. A Magnitude is either a Line or a Lineate.

The Common affections of a magnitude are hitherto declared: The Species or kindes doe follow: for other then this division our authour could not then meete withall.

2. A Line is a Magnitude onely long.

As are ae. io. and uy. such a like Magnitude is conceived in the measuring of waies, or distance of one place from another: And by the difference of a lightsome place from a darke: Euclide at the 2 d j. defineth a line to be a length void of breadth: And indeede length is the proper difference of a line, as breadth is of a face, and solidity of a body.

3. The bound of a line is a point.

Euclide at the 3. d j. saith that the extremities or ends of a line are points. Now seeing that a Periphery or an hoope line hath neither beginning nor ending, it seemeth not to bee bounded with points: But when it is described or made it beginneth at a point, and it endeth at a pointe. Wherefore a Point is the bound of a line, sometime actu, in deed, as in a right line: sometime potentiâ, in a possibility, as in a perfect periphery. Yea in very deede, as before was taught in the definition of continuum, 4 e. all lines, whether they bee right lines, or crooked, are contained or continued with points. But a line is made by the motion of a point. For every magnitude generally is made by a geometricall motion, as was even now taught, and it shall afterward by the severall kindes appeare, how by one motion whole figures are made: How by a conversion, a Circle, Spheare, Cone, and Cylinder: How by multiplication of the base and heighth, rightangled parallelogrammes are made.

4. A Line is either Right or Crooked.

This division is taken out of the 4 d j. of Euclide, where rectitude or straightnes is attributed to a line, as if from it both surfaces and bodies were to have it. And even so the rectitude of a solid figure, here-after shall be understood by a right line perpendicular from the toppe unto the center of the base. Wherefore rectitude is propper unto a line: And therefore also obliquity or crookednesse, from whence a surface is judged to be right or oblique, and a body right or oblique.

5. A right line is that which lyeth equally betweene his owne bounds: A crooked line lieth contrariwise. 4. d. j.

Now a line lyeth equally betweene his owne bounds, when it is not here lower, nor there higher: But is equall to the space comprehended betweene the two bounds or ends: As here ae. is, so hee that maketh rectum iter, a journey in a straight line, commonly he is said to treade so much ground, as he needes must, and no more: He goeth obliquum iter, a crooked way, which goeth more then he needeth, as Proclus saith.

6. A right line is the shortest betweene the same bounds.

Linea recta, a straight or right line is that, as Plato defineth it, whose middle points do hinder us from seeing both the extremes at once; As in the eclipse of the Sunne, if a right line should be drawne from the Sunne, by the Moone, unto our eye, the body of the Moone beeing in the midst, would hinder our sight, and would take away the sight of the Sunne from us: which is taken from the Opticks, in which we are taught, that we see by straight beames or rayes. Therfore to lye equally betweene the boundes, that is by an equall distance: to bee the shortest betweene the same bounds; And that the middest doth hinder the sight of the extremes, is all one.

7. A crooked line is touch'd of a right or crooked line, when they both doe so meete, that being continued or drawne out farther they doe not cut one another.

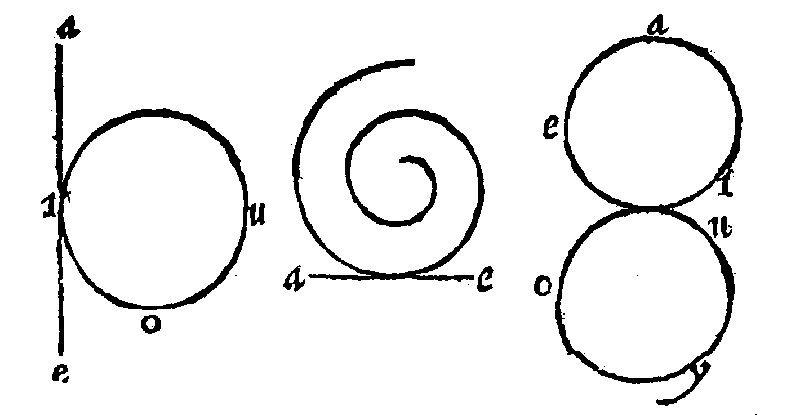
Tactus, Touching is propper to a crooked line, compared either with a right line or crooked, as is manifest out of the 2. and 3. d 3. A right line is said to touch a circle, which touching the circle and drawne out farther, doth not cut the circle, 2 d 3. as here ae, the right line toucheth the periphery iou. And ae. doth touch the helix or spirall. Circles are said to touch one another, when touching they doe not cutte one another, 3. d 3. as here the periphery doth aej. doth touch the periphery ouy.

Therefore

8. Touching is but in one point onely. è 13. p 3.

This Consectary is immediatly conceived out of the definition; for otherwise it were a cutting, not touching. So Aristotle in his Mechanickes saith; That a round is easiliest mou'd and most swift; Because it is least touch't of the plaine underneath it.

9. A crooked line is either a Periphery or an Helix. This also is such a division, as our Authour could then hitte on.

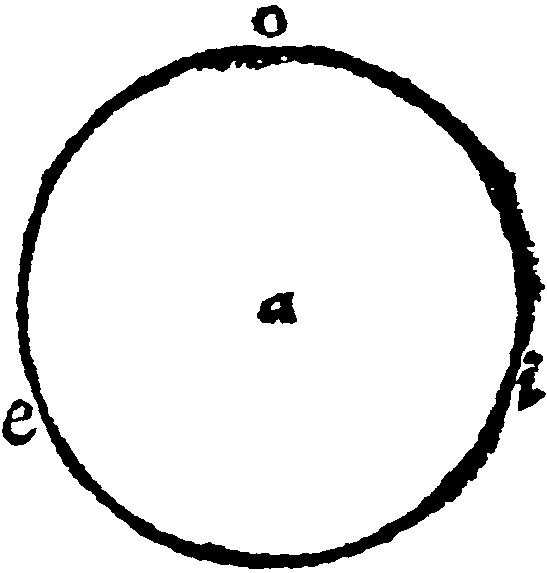
10. A Periphery is a crooked line, which is equally distant from the middest of the space comprehended.

Peripheria, a Periphery, or Circumference, as eio. doth stand equally distant from a, the middest of the space enclosed or conteined within it.

Therefore

11. A Periphery is made by the turning about of a line, the one end thereof standing still, and the other drawing the line.

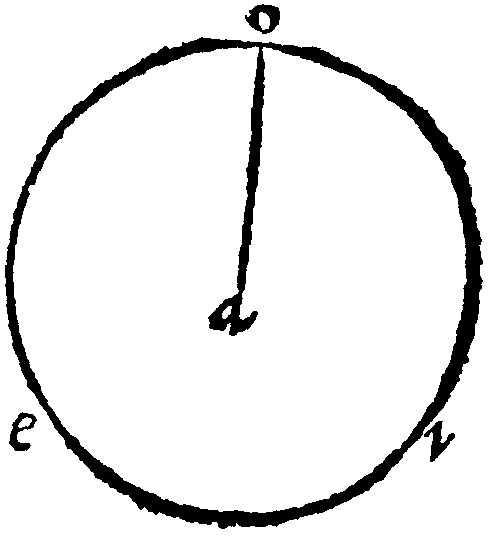
As in eio. let the point a stand still: And let the line ao, be turned about, so that the point o doe make a race, and it shall make the periphery eoi. Out of this fabricke doth Euclide, at the 15. d. j. frame the definition of a Periphery: And so doth hee afterwarde define a Cone, a Spheare, and a Cylinder.

Now the line that is turned about, may in a plaine, bee either a right line or a crooked line: In a sphericall it is onely a crooked line; But in a conicall or Cylindraceall it may bee a right line, as is the side of a Cone and Cylinder. Therefore in the conversion or turning about of a line making a periphery, there is considered onely the distance; yea two points, one in the center, the other in the toppe, which therefore Aristotle nameth Rotundi principia, the principles or beginnings of a round.

12. An Helix is a crooked line which is unequally distant from the middest of the space, howsoever inclosed.

Hæc tortuosa linea, This crankled line is of Proclus called Helicoides. But it may also be called Helix, a twist or wreath: The Greekes by this word do commonly either understand one of the kindes of Ivie which windeth it selfe about trees & other plants; or the strings of the vine, whereby it catcheth hold and twisteth it selfe about such things as are set for it to clime or run upon. Therfore it should properly signifie the spirall line. But as it is here taken it hath divers kindes; As is the Arithmetica which is Archimede'es Helix, as the Conchois, Cockleshell-like: as is the Cittois, Iuylike: The Tetragonisousa, the Circle squaring line, to witt that by whose meanes a circle may be brought into a square: The Admirable line, found out by Menelaus: The Conicall Ellipsis, the Hyperbole, the Parabole, such as these are, they attribute to Menechmus: All these Apollonius hath comprised in eight Bookes; but being mingled lines, and so not easie to bee all reckoned up and expressed, Euclide hath wholly omitted them, saith Proclus, at the 9. p. j.

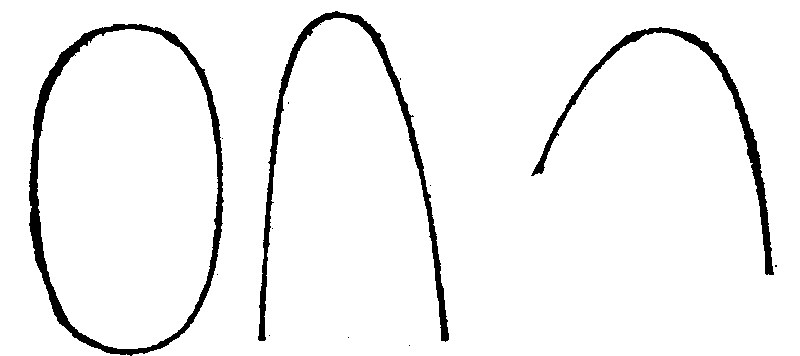
13. Lines are right one unto another, whereof the one falling upon the other, lyeth equally: Contrariwise they are oblique. è 10. d j.

Hitherto straightnesse and crookednesse have beene the affections of one sole line onely: The affections of two lines compared one with another are Perpendiculum, Perpendicularity and Parallelismus, Parallell equality; Which affections are common both to right and crooked lines. Perpendicularity is first generally defined thus:

Lines are right betweene themselves, that is, perpendicular one unto another, when the one of them lighting upon the other, standeth upright and inclineth or leaneth neither way. So two right lines in a plaine may bee perpendicular; as are ae. and io. so two peripheries upon a sphearicall may be perpendiculars, when the one of them falling upon the other, standeth indifferently betweene, and doth not incline or leane either way. So a right line may be perpendicular unto a periphery, if falling upon it, it doe reele neither way, but doe ly indifferently betweene either side. And in deede in all respects lines right betweene themselves, and perpendicular lines are one and the same. And from the perpendicularity of lines, the perpendicularity of surfaces is taken, as hereafter shall appeare. Of the perpendicularity of bodies, Euclide speaketh not one word in his Elements, & yet a body is judged to be right, that is, plumme or perpendicular unto another body, by a perpendicular line.

Therefore,

14. If a right line be perpendicular unto a right line, it is from the same bound, and on the same side, one onely. ê 13. p. xj.

Or, there can no more fall from the same point, and on the same side but that one. This consectary followeth immediately upon the former: For if there should any more fall unto the same point and on the same side, one must needes reele, and would not ly indifferently betweene the parts cut: as here thou seest in the right line ae. io. eu.

15. Parallell lines they are, which are everywhere equally distant. è 35. d j.

Parallelismus, Parallell-equality doth now follow: And this also is common to crooked lines and right lines: As heere thou seest in these examples following.

Parallell-equality is derived from perpendicularity, and is of neere affinity to it. Therefore Posidonius did define it by a common perpendicle or plum-line: yea and in deed our definition intimateth asmuch. Parallell-equality of bodies is no where mentioned in Euclides Elements: and yet they may also bee parallells, and are often used in the Optickes, Mechanickes, Painting and Architecture.