
Полная версия
Сакральное значение чисел. Духовные истины на языке математики
Как бы ни были резонны все эти рассуждения относительно 2, 3 и 5, они полностью упускают суть вопроса. На деле это не имеет никакого отношения к супружеству. Но греки сделали все, что смогли, чтобы представить «нечто», используя слова и концепции, доступные их языку. Это то, что можно сделать с помощью любого вербального языка, в попытках обсудить «нечто» такое, что невозможно выразить словами.
Допустим, что в первый раз мы промахнулись. Давайте попытаемся еще раз, руководствуясь полной информацией о древнегреческом числовом символизме. Древние греки явно тяготели к философии. Числа 2, 3 и 5 были абстрактными концепциями. Женское число 2 и мужское число 3 считались самыми базовыми принципами, или законами, жизни. В совокупности они включали в себя все полярные противоположности (все формы двойственности) на каждом из земных планов. Древние греки называли десять пар полярных противоположностей, которые включали свет и тьму, мужчину и женщину, добро и зло. Они рассуждали так: если эти качества, пребывающие в фундаментальном конфликте друг с другом, можно было бы гармонизировать и заставить функционировать сообща (они использовали термин «вступить в брак»), то это дало бы человеку способность прожить позитивную, продуктивную и эффективную жизнь. Тем самым число 5 символизировало искомое состояние гармонии.
Это объяснение основано на полной информации. Его суть так же важна сейчас, как была важна во времена древних греков: следует жить гармонично в мире, полном полярных противоположностей. Это поразительная формулировка духовных принципов, но тем не менее она не дает нам ничего, кроме информации. После того как мы закончили все эти рассуждения, мы снова возвращаемся к своим собственным мыслям и задаемся вопросом: «Итак, что мне следует делать сейчас?» Обычно, получив надлежащее объяснение, мы приобретаем способность действовать, руководствуясь обретенным пониманием. Здесь этого не происходит, поскольку передачи персонального значения и смысла не произошло, равно как и никакого непосредственного обучения на опыте. Это объяснение лишь более полно раскрыло символы, которые были непонятны поначалу и остались таковыми. Язык этих числовых символов так и остался иностранным для нашего мышления.
Искусство интерпретации – это главный навык, необходимый для того, чтобы пользоваться числовым символизмом. Чтобы научиться интерпретировать, мы должны вернуться к истокам математики, чтобы узнать, как и почему числа превратились в метафизические символы. Числа, используемые символически, являются математическими во всех смыслах этого слова. История числового символизма и история математики были неотделимы друг от друга примерно до 500 года нашей эры. Очень важно в самом начале этого краткого исторического экскурса отметить следующее: помимо того, что числа использовали для счета, измерения и подсчетов, их всегда наделяли культурными и метафизическими атрибутами.
Сегодня математика представляет собой чисто абстрактную систему. Однако в самом начале числа не были абстракцией. Первые попытки вести счет, которые были сделаны тысячелетия назад, выглядят невообразимо странно для современного ума. Тогда не было написания чисел, которым мы пользуемся сегодня, не было даже слов для обозначения этих чисел. Подсчет нередко означал вырезание линий на дереве или камне или оставление отпечатков на глиняных табличках. Конкретное число записывали, вырезая такое же количество линий: для обозначения 6 требовалось шесть линий, для обозначения 28 – двадцать восемь. Привычная косая черта по диагонали, обозначающая повторяющиеся 5, была неизвестна. Некоторые древние народы вели счет, указывая на разные части тела. Пример такого счета существует и в наши дни в одном из племен, населяющих остров Папуа: 1 – это мизинец на правой руке; 2 – безымянный палец на правой руке; 3 – средний палец на правой руке; 4 – указательный палец на правой руке; 5 – большой палец на правой руке; и так далее до числа 12, которое обозначает нос; 13 – рот; 14 – левое ухо и так далее[6]. Усложненной версией такой формы счета был счет на пальцах, который сохранялся в Европе примерно до 1700-х годов. Древние римляне могли считать на пальцах от одного до десяти тысяч.
В далеком прошлом для чисел, используемых для счета, нередко не существовало слов. Количество чего-то было частью самого слова. Так, в современном английском мы меняем существительные и добавляем «s» на конце во множественном числе (например, «tree» («дерево») – «trees» («деревья»)). В арабском языке до 700 года нашей эры слово «radjulun» означало одного человека, «radjulan» – двух человек, a «ridjulun» – несколько человек[7]. Следы точно такого же подхода мы можем найти и в современном английском языке, в таких выражениях, как «пара волов» («yoke of oxen») и «упряжка лошадей» («team of horses»). Сегодня может показаться неважным, что в некоторых языках были слова для обозначения одной вещи и двух вещей. Но на заре развития математики в некоторых культурах не существовало чисел больше двух или трех. В разное время и в разных странах 2, 3, 4 и, чаще всего, 10 (поскольку у нас 10 пальцев на руках) были пределами счета. Сегодня в это верится с трудом. В наши дни школьники хорошо знакомы и с миллионами, и с миллиардами. Однако даже в современном мире в южных странах живет племя, у которого самым большим числом является 2. Они считают от 1 до 5 следующим образом: 1, 2, 2'1,2'2, 2,2,1[8]. Многие древние народы умели считать от 1 до 9, а после этого они просто говорили «много». Значения корней немецких числительных говорят о том, что некогда самым большим числом было 10. Сотню обозначали как «десять десяток», а тысяча была «сильной десяткой десяток». Наше слово, обозначающее миллион, имеет примерно такую же историю. Это комбинация латинского слова mille, что означает «тысяча» и усиливающего слова «опе». В сочетании «mille-опе» означает «много тысяч»[9].
Сегодня вся наша математическая система состоит из всего лишь десяти чисел – 0 и чисел от 1 до 9. Если мы хотим идти дальше, то мы должны комбинировать цифры. Следовательно, мы имеем то, что называется десятеричной системой. В прошлом использовались и другие системы, не десятеричные. У китайцев некогда система счисления была основана на 2. В качестве основы использовали и 5, и 20. Такие системы были у народов майя, ацтеков и друидов. Доказательством того, что друиды пользовались двадцатеричной системой, является слово, обозначающее 80 в современном французском языке – «quatre-vingts», что означает «четыре двадцатки». В математике древних шумеров использовали две различные системы счисления: для повседневных подсчетов они пользовались десятеричной системой, а для астрономических вычислений – шестидесятеричной. Другими словами, прежде чем они начинали комбинировать числа для того, чтобы выразить большие величины, у них в распоряжении было шестьдесят чисел.
У шумеров, как у любого другого древнего народа, числа имели священный и философский смысл. Числа отождествляли с богами. Основные взаимосвязи между богами устанавливали в том числе по числам, на которые число 60 делилось без остатка. Сегодня вместо слова «боги» мы можем поставить «духовные силы» или «космические законы». По всей видимости, числа, на которые 60 делилось без остатка, демонстрировали взаимоотношения между богами потому, что эти взаимосвязи можно было установить непосредственно с помощью математики.
Шумеры находили свои священные числа в природе, выводя их, в частности, из продолжительности года и тех объектов, которые они наблюдали в небе; так поступали многие цивилизации того времени. Люди считали солнце, луну и звезды божественными созданиями и полагали, что циклы их путешествия по орбитам отражают деятельность богов. В настоящее время известно, что у шумеров, как и у многих других народов древности, были великолепные астрономы, точность наблюдений которых намного превосходила ту, которую мы приписывали им. В некоторых случаях (например, при предсказании лунных затмений) древние астрономы были практически так же точны, как современные ученые! Несмотря на эти знания, продолжительность календарного года шумеров составляла 360 дней, а не 365 % дня, как на самом деле. Это определенно создавало удобства, потому что есть много чисел, на которые 360 делится без остатка, тогда как действительная продолжительность года не делится без остатка вообще, из-за !4 дня. Сначала это расхождение тревожило меня. Вся космология шумеров была основана на числе 360. Однако, как оказалось, шумеры были прекрасно осведомлены об истинной продолжительности года, и поэтому разработали метод, позволяющий суммировать пять дополнительных дней без ущерба счету лет. То же самое практиковали астрономы и других древних цивилизаций – друиды, индийские арии, египтяне, майя, инки и китайцы; у всех у них календарный год состоял из 360 дней и включал пять дополнительных дней. Я ломал голову над тем, насколько осознанно шумеры манипулировали числами, чтобы их числовой символизм работал. Какое-то время спустя я узнал, что «в какой-то момент во время эры Рака мы приобрели пять дополнительных дней, так называемые эфиопские дни; ранее Земля совершала свое вращение вокруг Солнца ровно за 360 дней»*. Это успокоило меня, потому что система духовных символов, без внутренней цельности и честности, не имеет никакой ценности. Как оказалось, многие цивилизации просто демонстрировали свое почтение к предшествующей им истории человечества. Это демонстрирует также, что реальность нашего мира меняется и предпосылки какой-либо системы мудрости могут утратить свою ценность по истечении определенного срока – если они основаны на физической реальности. В наши дни нет никаких оснований делать числа 60 или 360 священными.
Шумеры мечтали структурировать вселенную с помощью чисел, но первые попытки этого были сделаны только через 1400 лет, во времена Пифагора. Под «структурой вселенной» шумеры понимали распространение своих знаний символизма чисел на объяснение всего происходящего в мире. Хотя древние шумеры не преуспели в этом, они оставили нам в наследство две вещи, которыми мы пользуемся до сих пор. То, что мы делим круг на 360 градусов, а час – на 60 минут, является культурным наследием той давно ушедшей цивилизации. Еще одна вещь, оставленная нам шумерами, – это изобретение подсчета числовых значений имен и слов. Это составляет тот фундамент, на котором работает современная нумерология, а также еще несколько других, менее известных форм числового символизма, например гематрия. Гематрия – это метод определения скрытых связей между словами, имеющими одинаковое нумерологическое значение. Просто поразительно, насколько сильна унаследованная сила культуры и традиции!
С появлением шумеров началась эпоха исторических письменных свидетельств. Несмотря на прогресс, которого к тому времени достигла математика, она пребывала в весьма примитивном состоянии с точки зрения современных стандартов. Написание чисел было весьма громоздким. А еще хуже то, что ими нельзя было пользоваться даже для простейших вычислений вроде сложения и вычитания. Такого рода ограничения сохранялись во всем мире примерно до 700 года нашей эры, когда в Индии изобрели так называемые арабские цифры, которыми мы пользуемся и по сей день.
До этого времени числа писали только для того, чтобы сделать заметки о количестве чего-то или записать результаты вычислений. Начиная с эпохи шумеров (5000 лет до нашей эры) и заканчивая примерно 1700 годами, люди считали на пальцах и счетах, выполняя сложение, вычитание, умножение и деление. Счеты представляли собой костяшки из дерева или камня, надетые на параллельно натянутые нити. Для вычислений использовали камушки и специальные фишки. Количество костяшек, символизирующих то или иное число, равнялось этому числу. Для обозначения числа 7, например, требовалось семь костяшек. В Европе колонки на счетах указывали поместное значение каждого числа. Колонка определяла, идет ли речь о единицах (1, 2, 3 и так далее до 9), десятках (10, 20, 30 и так далее до 90), сотнях (100, 200, 300 и так далее до 900) и так далее. Ноль при работе со счетами не учитывали. Колонки, представляющие ноль, просто оставляли пустыми.
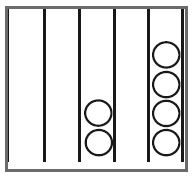
Рис. 1. Число 204, отложенное на счетах
На рис. 1 показано, как на счетах выглядело число 204. Как бы ни было важно поместное значение чисел при операциях на счетах, эту технику не включали в работу с написанными числами вплоть до XV века.
Весьма любопытно, что в Китае вместо костяшек в счетах использовали маленькие деревянные или бамбуковые палочки. Возможно, это связано с тем, что изначально при работе с «И-Цзином» («Книгой Перемен») пользовались именно палочками. Сегодня для простоты вместо палочек кидают три монеты. И-Цзин базируется на 64 гексаграммах. Гексаграмма – это шесть линий, которые могут быть прерывистыми или сплошными (рис. 2). При истолковании смысл гексаграммы определяют по конкретному сочетанию линий и порядку их расположения. Чередование прерывистых и сплошных линий наводит на мысль о древней китайской двоичной системе счисления, поскольку мы имеем лишь два символа. Это еще один пример того, как древние народы использовали математику для выражения концепций мудрости и духовности.

Рис. 2. Эта взятая в качестве примера гексаграмма по номером 17 называется Суй («Следование»). Ее краткое истолкование звучит следующим образом: «Радость движения ведет к следованию. Идея следования как приспособление к велениям времени произрастает из этого образа»
Значительный прогресс в написании чисел произошел, когда в качестве числовых систем стали использовать алфавиты. Это изобретение греки сделали примерно за 450 лет до нашей эры, а потом его переняли древние иудеи. В алфавитах обоих народов первые девять букв выступали также в качестве цифр от 1 до 9. Следующие девять букв представляли десятки, от 10 до 90, а последние девять были сотнями, от 100 до 900. Колоссальным преимуществом таких алфавитных чисел была простота. До появления алфавитных чисел письменные знаки существовали только для 1, 5, 10, 100 и так далее. Остальные числа писали, повторяя и комбинируя эти базовые цифры. Точно так же как на счетах, 4, например, записывали, четыре раза написав «1»; 40 записывали в виде значка 10, повторенного четыре раза. Давайте рассмотрим конкретный пример. В Древнем Египте 1 представляла собой вертикальную линию, а 10 – арку. Вот как они изображали число 44: ││││∩∩∩∩. Алфавитные же числа предлагали букву/число для всех единиц, десятков и сотен. Поэтому 44 можно было написать как 404 (используя, естественно, соответствующие греческие буквы или буквы иврита). Чтобы написать число 404, что мы сейчас делаем, вставив 0, эти народы писали 4004, и при этом не испытывали ни малейших страданий по поводу того, что в столбце десятков у них ничего не стояло. «Для примитивного человека, делающего подсчеты, число – это всегда число, количество, и только число может иметь символ»[10]. Именно так и поступали древние египтяне и большинство других древних народов, и точно так же они проделывали это на счетах. Египтяне обозначали число 100 как 9, поэтому 404 они писали так: ││││9999. Благодаря алфавитным числам впервые стало возможно использовать написанные числа для совершения подсчетов, какими бы неуклюжими и громоздкими они не казались нам сейчас.
Алфавитные числа явно стали предтечей современной нумерологической практики приписывать буквам числовые значения, в том числе пифагорейской и каббалистической нумерологии. На первых порах алфавитные числа были чисто математической разработкой. Однако вскоре символизм чисел распространился на буквы и слова, составленные из этих букв. Числовой символизм, подобно всем духовным символическим системам, склонен развиваться в двух направлениях. Во-первых, система символов медленно созревает по мере того, как с ней работают, поколение за поколением, представители данной культуры. Постепенно обветшалые элементы подвергаются ректификации и очищению благодаря многократным пересказам. Происходит своеобразный органический процесс отсева, благодаря которому базовые истины о человеческой природе и жизни принимают чистую, архетипическую форму. Однако в какой-то момент эта достойная работа приносит в жертву систему символов, порождая мудрость и духовное знание священного характера. При развитии во втором направлении какой-нибудь одаренный индивид делает настолько глубокий и важный вклад во всю систему символов, что та приобретает глубокое видение и пророческие возможности.
Такой человек появился на свет в Греции в VI веке до нашей эры; имя этого человека – Пифагор. Он был математиком, философом, мистиком, учителем и одним из самых образованных людей в истории человечества. Он разработал геометрическую теорему, которую до сих пор изучают в школах. Он основал школу мистерий, которая была знаменита в то время. Современная самая популярная форма нумерологии, нумерология Пифагора, названа в честь этого человека. Однако, как мы увидим, практически ничего из учения Пифагора и его математических практик не вошло в сегодняшнюю пифагорейскую нумерологию. Единственное, что ее объединяет с древним учением Пифагора, это, во-первых, использование десятеричной системы, а во-вторых, особый акцент, который делается на первых десяти числах. Связь между Пифагором и современной нумерологией, названной в его честь, настолько слаба, что есть большое искушение предположить, что имя этого великого человека выбрали совершенно случайно, просто для того, чтобы тем самым оказать ему честь!
Даже если это так, то Пифагор все равно сделал монументальный вклад. Этим вкладом стала его концепция о том, что все в жизни имеет математический базис: «принцип, согласно которому искусство, психологию, философию, ритуалы, математику и даже спорт следует считать аспектами единой науки гармонии»*. В Древней Греции существовало пять областей математики: арифметика и геометрия (греки считали это одним и тем же), астрономия, музыка и стереометрия (измерение объемов). Задача структурирования философии в соответствии с математическими принципами потребовала духовного видения высшего порядка, которое смогло бы структурировать принципы жизни в числовых понятиях. Похоже, что эта мечта была сродни той, которая будоражит умы современных физиков – получить теорию Единого поля, объединяющую все базовые силы вселенной и дающую им единое объяснение.
Главным элементом пифагорейского числового символизма был, без всяких сомнений, любимый тетрактис (рис. 3). Это расположение десяти точек в форме треугольника с четырьмя точками в основании, затем тремя, двумя и, наконец, одной точкой на вершине; эта структура символизирует создание Вселенной. Тетрактис известен также как Принцип Здоровья. Он был основан на идее о том, что существует десять принципов, или универсальных законов, которые рождают и сохраняют существование всего существующего в мироздании. Это мысль, на которую может опереться современный ум; концепция, содержащая небольшое количество базовых элементов, которые дают начало всему остальному. Это также давно забытое соображение о том, что все числа в пифагорейской нумерологии обычно сводили к одной-единственной цифре. Однозначные числа представляют собой основные значения натуральных чисел (целых чисел от 1 до бесконечности). Чтобы свести число 39 к одной цифре, например, нужно сложить 3 и 9. В сумме это дает 12, поэтому мы снова складываем 1 и 2, и получаем 3. В результате мы можем сказать, что 39 сводится к 3.

Рис. 3. Тетрактис Пифагора
Тетрактис на самом деле состоял из четырех ключевых чисел, ответственных за все мироздание: 1, 2, 3 и 4. Цифра 1 – это Единство[11] неделимая единица, называемая монадой; основа всего мироздания, которая геометрически выражается точкой. Двойка была женским (генеративным) принципом, и ее геометрическим символом была линия. Тройка была мужским (каузальным (причинным)) принципом, и ее геометрическим символом была плоскость. Четверка была единицей измерения вселенной, и геометрически ее символизировал куб. Древние греки видели глубокую связь между любыми двумя или несколькими числами и общей суммой, которая в данном случае выражалась так: 1 + 2 + 3 + 4=10. Любопытно, что числа 1, 2 и 3 вообще не считали числами; они были принципами или основными законами Вселенной. Числа были осязаемыми, проявленными вещами, и они начинались с 4. Это особенно относилось к 1, из-за уникальной роли единицы как числа, от которого происходят все прочие числа. Эти верования были настолько сильны, что в 1585 году, через две тысячи лет после Пифагора, математик Майкл Стевин предложил формальное доказательство того, что 1 является числом!
Священное значение Тетрактиса было расширено, поскольку десять точек образовывали треугольник, и греки называли такие числа треугольными числами. Известны и другие треугольные числа – 3, 6 и 15 и так далее (рис. 4). Греки также высоко ценили квадратные числа, на основании того, что существуют определенные количества точек, формирующие квадрат. Вот пример квадратных чисел: 4, 9 и 16 и так далее (рис. 5). Геометрию считали откровением, полученным от Бога, и любые взаимосвязи, которые греки могли установить между числами и геометрическими фигурами, демонстрировали нечто священное, а также определяли глубинные структуры жизни. Пифагорейцы верили, что все должно иметь физическое проявление. Даже мысли, чувства и концепции (например, справедливость) они считали в какой-то степени физическими. Это вовсе не так глупо, как может показаться на первый взгляд. Задумайтесь вот о чем. Сегодня у нас есть инструменты, способные регистрировать и измерять мысли в виде потока электронов, излучаемого мозгом. Поэтому, хотя мы не считаем мысли чем-то таким же физическим, как, скажем, камни и деревья, мы должны согласиться с древними греками, что это все лишь вопрос разной степени одного и того же качества.

Рис. 4. Треугольные числа 3, 6 и 15

Рис. 5. Квадратные числа 4,9 и 16
В космогонии греков не было ничего абстрактного. Греки считали, что все, что существует, физически или в умах людей, буквально состоит из монад, то есть из единиц или геометрических точек. Знаменитое высказывание Пифагора «Все сущее – это числа» вовсе не обязательно должно иметь тот смысл, который приписывают ему в наши дни. Сегодня, исходя из точки зрения физики, мы полагаем, что математические связи объясняют физическую реальность. Современные специалисты по числовому символизму придерживаются сходной точки зрения, но исходят из убеждения, что числа выражают природу духовных принципов. Пифагор же просто имел в виду то, что любая данная конкретная вещь или событие состоит из некоторого количества монад. Все сущее было числом. В буквальном смысле этого слова.
Конечной целью числового символизма Пифагора была гармония; в наши дни целью является понимание психологии, духовные инсайты и предсказания. В отличие от нас, греки не делали акцент на значении отдельных чисел. Гармония между числами устанавливалась посредством сложения, умножения и деления, и именно поэтому разработки древних греков так сложны для понимания. Вот несколько примеров их принципов гармонии.
Изобильные числа. Это числа, сумма делителей которых больше самого числа. Двенадцать является изобильным числом, потому что 1, 2, 3, 4 и 6 (делители, числа, на которые делится 12) в сумме дают 16 (на четыре больше, чем 12).
Дефектные числа. Это числа, сумма делителей которых меньше самого числа. Десять является дефектным числом, потому что 1, 2 и 5 (его делители, числа, на которые делится 10) в сумме дают 8 (на два меньше, чем 10).
Совершенные числа. Это числа, сумма делителей которых равна самому числу. Шесть является совершенным числом, потому что 1, 2 и 3 (числа, на которые 6 делится без остатка) в сумме тоже дают 6.
Дружественные числа. Это два различных числа, делители каждого из которых в сумме дают другое число. Числа 220 и 284 являются дружественными, потому что одиннадцать чисел, на которые делится 220, в сумме дают 284, а пять чисел, на которые без остатка делится 284, в сумме дают 220.
Четно-четные, нечетно-нечетные и четно-нечетные числа. Эти числа образуются при умножении четных (женских) и нечетных (мужских) чисел. Так, 2 × 2 = 4, которое является четно-четным числом, потому что оба сомножителя являются четными числами. Десять является четно-нечетным числом, потому что это число является результатом умножения 2 (четного числа) на 5 (нечетное число). Когда перемножаются два нечетных числа, например 5 и 7, в результате получается нечетно-нечетное число – 35.



