Цифровые устройства. Учебник для колледжей

Y2 = [(X1′·X3′) \/ (X1·X2·X3)]′′ = [(X1′·X3′)′· (X1·X2·X3)′]′ =

= [(X1′/X3′) / (X1/X2/X3)].

Подсчитываем требуемое количество элементов: 4 элемента 2И-НЕ (из них – 2 элемента для выполнения логического отрицания) +1 элемент 3И-НЕ.

Подбираем ИМС: по одной ИМС КР1533ЛА3 и КР1533ЛА4.

Строим схему ЦУ в базисе И-НЕ (рис.2.33).

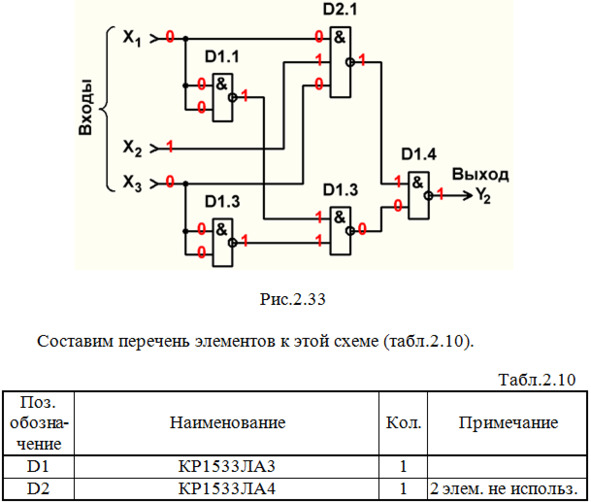
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.33 и красную строку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 1 + 1/3 = 1 + 1,33 = 1,33 корпуса; T = 3τ.

Пример 3. МДНФ (см. пример 3 из темы 2.2):

Y3 = X3′ \/ X1′·X2.

Переходим к базису И-НЕ:

Y3 = (X3′ \/ X1′·X2)′′ = [(X3′)′ \/ (X1′·X2)′]′ = (X3) / (X1′ / X2).

Обратим внимание, что в МДНФ переменная была с отрицанием, затем после применения закона де Моргана у нее появилось второе отрицание, что по закону двойной инверсии дает прямое значение X3. На будущее следует иметь в виду весьма простое правило: если в логическом выражении базиса И, ИЛИ, НЕ имеется минтерм, содержащий только одну переменную, то при переходе к базису И-НЕ эта переменная будет обязательно менять свое значение на противоположное: если она была без отрицания, то будет с отрицанием; если же она была с отрицанием, то будет без него.

Подсчитываем требуемое количество элементов: 3 элемента 2И-НЕ (из них – 1 элемент для логического отрицания).

Подбираем микросхему: одна микросхема КР1533ЛА3.

Строим схему ЦУ в базисе И-НЕ (рис.2.34):

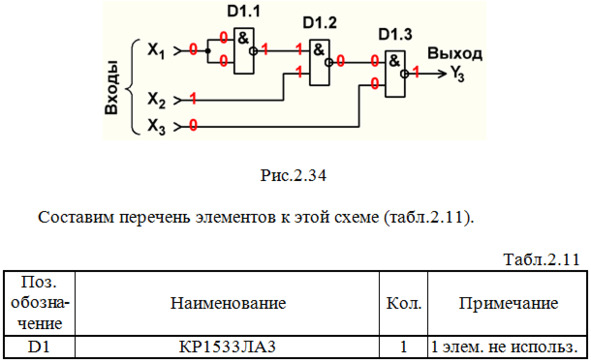
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.34 и красную строку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 3/4 = 0,75 корпуса; T = 3τ.

2.5. Переход к базису ИЛИ-НЕ. Подбор микросхем, построение и анализ работы схем ЦУ в базисе ИЛИ-НЕ

Аналогично описанному в предыдущем параграфе переходу к базису И-НЕ от МДНФ производится переход к базису ИЛИ-НЕ, только теперь уже от МКНФ:

1. Используется закон двойного отрицания (двойной инверсии):

A = A′′

2. Применяется вторая форма закона де Моргана:

(B·C·D·…)′ = B′ \/ C′ \/ D′ \/…

3. Полученное логическое выражение рекомендуется записать с использованием символа «стрелка Пирса» (смотрите табл.1.1), например:

(X1 \/ X2)′ = X1 ↓ X2.

П р и м е ч а н и е :

В итоговом логическом выражении должны содержаться только операции ИЛИ-НЕ. Но кроме них, как правило, остаются все-таки операции НЕ, которые в данном случае следует выполнять с помощью элементов 2ИЛИ-НЕ путем объединения входов этих элементов.

Пример 1. МКНФ (см. пример 4 из темы 2.2):

Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1′ \/ X2 \/ X3′).

Переходим к базису ИЛИ-НЕ. Для этого сначала используем закон двойного отрицания:

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 3 элемента – для отрицания) +2 элемента 3ИЛИ-НЕ.

Подбираем микросхемы: две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.

Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.35).

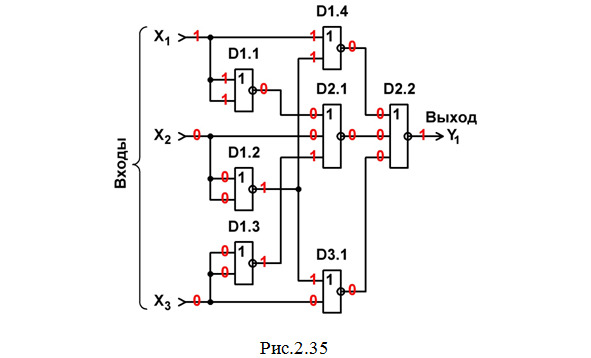
Составляем перечень элементов к этой схеме (табл.2.12).

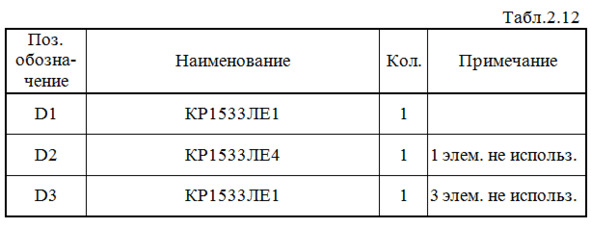
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.35 и синюю строку в табл.2.1).

Определим аппаратурные затраты и задержку:

W = 1 + 2/3 + 1/4 = 1 + 0,67 + 0,25 = 1,92 корпуса; T = 3τ.

Пример 2. МКНФ (см. пример 5 из темы 2.2):

Y2 = (X1 \/ X3′) · (X1′ \/ X3) · (X1′ \/ X2).

Переходим к базису ИЛИ-НЕ:

Y2 = [(X1 \/ X3′) · (X1′ \/ X3) · (X1′ \/ X2)]′′ =

= [(X1 \/ X3′) ′ \/ (X1′ \/ X3) ′ \/ (X1′ \/ X2)′]′ =

= (X1 ↓ X3′) ↓ (X1′ ↓ X3) ↓ (X1′ ↓ X2).

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 2 элемента – для отрицания) +1 элемента 3ИЛИ-НЕ.

Подбираем микросхемы: две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.

Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.36).

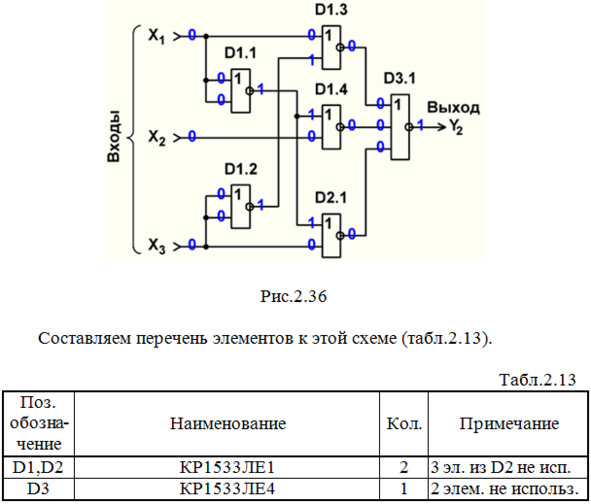
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.36 и синюю строку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 1 + 1/4 + 1/3 = 1 + 0,25 + 0,33 = 1,58 корпуса; Т = 3τ.

Пример 3. МКНФ (см. пример 6 из темы 2.2):

Y3 = (X2 \/ X3′) · (X1′ \/ X3′).

Переходим к базису ИЛИ-НЕ:

Y3 = [(X2 \/ X3′) · (X1′ \/ X3′)]′′ = [(X2 \/ X3′)′ \/ (X1′ \/ X3′)′]′ =

= [(X2 ↓ X3′) ↓ (X1′ ↓ X3′)].

Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 2 элемента – для отрицания).

Подбираем микросхемы: две микросхемы КР1533ЛЕ1.

Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.37).

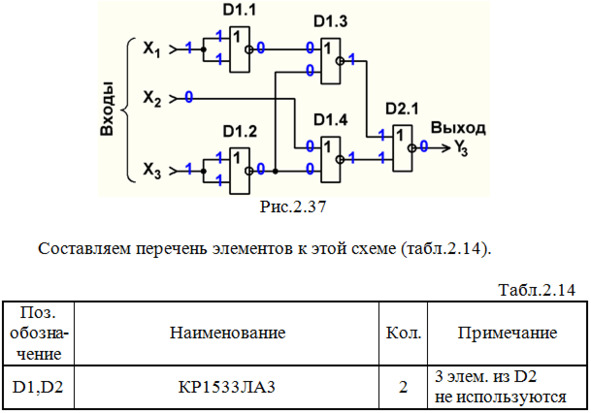
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.37 и синюю строку в табл.2.2).

Определим аппаратурные затраты и задержку:

W = 1 + 1/4 = 1 + 0,25 = 1,25 корпуса; T = 3τ.

2.6. Использование в схемах элементов разных базисов и комбинированных микросхем

Очень часто для достижения лучшего быстродействия или уменьшения аппаратурных затрат в схемах цифровых устройств используют элементы разных базисов. Приведем пример:

Пример 1. МКНФ (см. пример 4 из темы 2.2):

Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1′ \/ X2 \/ X3′).

В данном логическом выражении базиса И, ИЛИ, НЕ преобразуем последний многочлен с использованием закона двойного отрицания и первого закона де Моргана:

(X1′ \/ X2 \/ X3′) = (X1′ \/ X2 \/ X3′)′′ = (X1′)′· (X2)′· (X3′)′ =

= X1 / X2′ / X3.

Теперь с учетом полученного результата исходное логическое выражение примет вид:

Y1 = (X1 \/ X2′) · (X2′ \/ X3) · (X1 / X2′ / X3).

Определим требуемое количество элементов: 1 элемент НЕ +2 элемента 2ИЛИ +1 элемент 3И-НЕ (для выполнения операции в третьей скобке) +1 элемент 3И.

Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛЛ1, КР1533ЛА4 и КР1533ЛИ3.

Строим схему ЦУ (рис. 2.38):

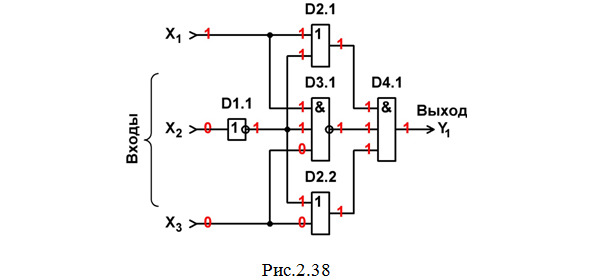
Составим перечень элементов к этой схеме (табл. 2.15).

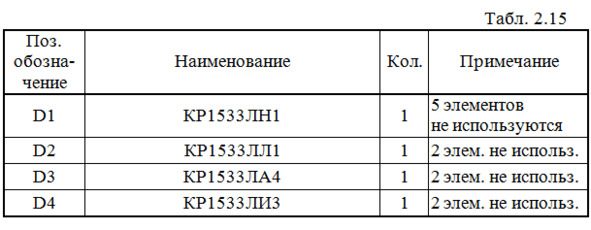
Выполним анализ работы ЦУ в статическом режиме для одной комбинации входных сигналов (см. рис.2.38 и красную строку в табл.2.1).

Определим аппаратурные затраты и задержку:

W = 1/6 + 2/4 + 1/3 + 1/3 = 0,17 + 0,5 + 0,33 + 0,33 =

= 1,33 корпуса; T = 3τ.

Полученные результаты сравним с этими же параметрами, характеризующими работу схемы рис. 2.27, построенной по исходной МКНФ:

W = 1,83 корпуса; T = 4τ.

Хорошо видно, что преобразование только лишь одного многочлена МКНФ и вытекающая из этого необходимость использования в схеме элементов разных базисов привело: во-первых, к уменьшению задержки (3τ вместо 4τ); и, во-вторых, к уменьшению аппаратурных затрат (1,33 корпуса вместо 1,83).

***

Иногда для достижения тех же целей увеличения быстродействия, уменьшения аппаратурных затрат, но в основном для уменьшения количества внешних соединений (то есть таких соединений, которые выполняются не внутри микросхемы, а снаружи путем монтажа) между микросхемами и элементами микросхем применяют комбинированные ИМС (смотрите, например, рис. 1.15 из параграфа 1.5). Приведем пример:

Пример 2. МДНФ (см. пример 1 из темы 2.2):

Y1 = X1′·X2′ \/ X2′·X3′ \/ X1·X2·X3.

Логическое отрицание, как и в указанном примере 1 из темы 2.2, будем делать с помощью тех же элементов НЕ из микросхемы КР1533ЛН1. А для выполнения остальных операций воспользуемся микросхемой КР1533ЛР13 (рис. 2.39).

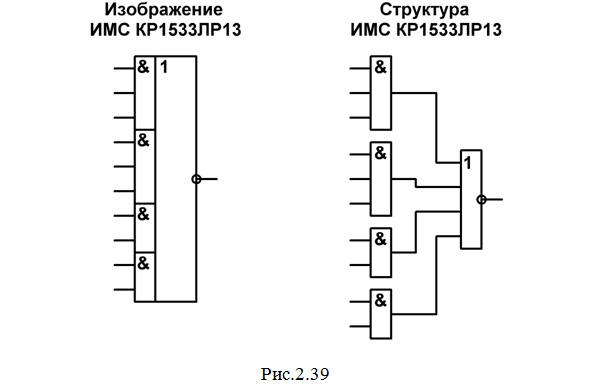
Но здесь нужно учесть, что в данной микросхеме на выходе стоит элемент ИЛИ-НЕ, поэтому выходной сигнал получится инвертированным. Чтобы получить на выходе все-таки прямое значение сигнала, выполним его повторное отрицание с помощью еще одного элемента НЕ из микросхемы КР1533ЛН1.

Строим схему ЦУ (рис. 2.40):

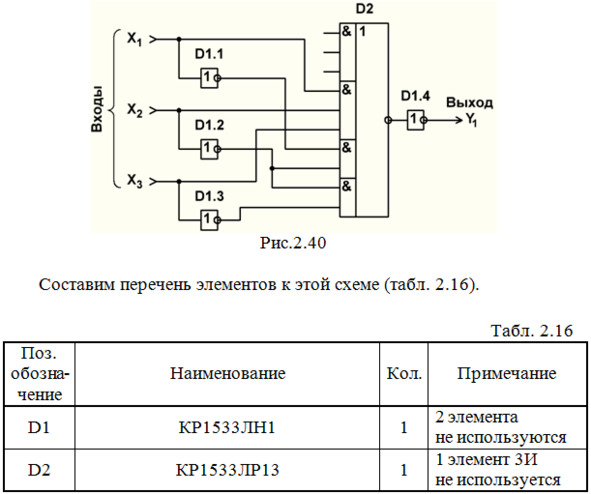
П р и м е ч а н и е: один элемент 3И из микросхемы КР1533ЛР13 получается лишним. В схеме рис. 2.40 его входы оставлены свободными, но этого делать нельзя! В микросхемах ТТЛ и ТТЛШ-структур входы лишних элементов обязательно следует куда-либо подключить, иначе данная ИМС работать не будет (смотрите тему 2.9).

Определим количество внешних соединений между элементами:

– в схеме рис. 2.25, построенной по исходной МДНФ: 8;

– в схеме рис. 2.40: 5.

Это подтверждает сказанное ранее: использование комбинированных ИМС уменьшает количество внешних соединений между элементами микросхем.

Подсчитаем аппаратурные затраты и задержку:

W = 4/6 + 4/5 = 0,67 + 0.8 = 1,47 корпуса; T = 4τ.

Полученные результаты сравним с этими же параметрами, характеризующими работу схемы рис. 2.25, построенной по исходной МДНФ:

W = 1,83 корпуса; T = 4τ.

Хорошо видно, что аппаратурные затраты уменьшились: 1,47 корпуса вместо 1,83.

Задержка вроде бы осталась той же: T = 4τ. Но соединительные линии внутри комбинированной микросхемы дают меньшую задержку сигналов, чем внешние соединения. Поэтому из-за уменьшения количества внешних соединений задержка на самом деле станет несколько меньше 4τ.

2.7. Сравнительная оценка качества схем

Сравнительный анализ качества схем, как уже было указано ранее, обычно производится по двум важнейшим критериям: задержке T и аппаратурным затратам W.

Если не предъявляются заранее поставленные особые требования к отдельным критериям, то поступают следующим образом:

– Отбрасывают варианты, обладающие самыми худшими характеристиками или по T, или по W, или по обоим параметрам одновременно.

– Из других схем (все они образуют так называемое множество Парето) отдают предпочтение более быстродействующим.

– В оставшихся вариантах с одинаковой минимальной задержкой выбирают наиболее экономичные схемы.

Для примера проведем сравнительную оценку качества схем, реализующих функцию Y1, которые были построены нами различными способами. Для этого сведем данные по T и W в небольшую таблицу (табл. 2.17).

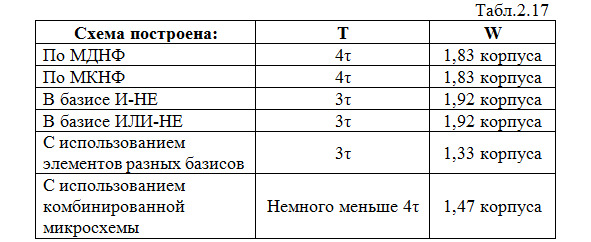
Сначала исключаем схемы, построенные по МДНФ и МКНФ, обладающие наибольшей задержкой. Затем исключаем схемы в базисах И-НЕ и ИЛИ-НЕ с наибольшими аппаратурными затратами.

В оставшихся двух вариантах, которые в данном случае и образуют множество Парето, выбираем как более быстродействующую схему, построенную с использованием элементов разных базисов.

2.8. Синтез и анализ работы ЦУ с 4 входами

Задана таблица истинности ЦУ, имеющего 4 входа (табл. 2.18).

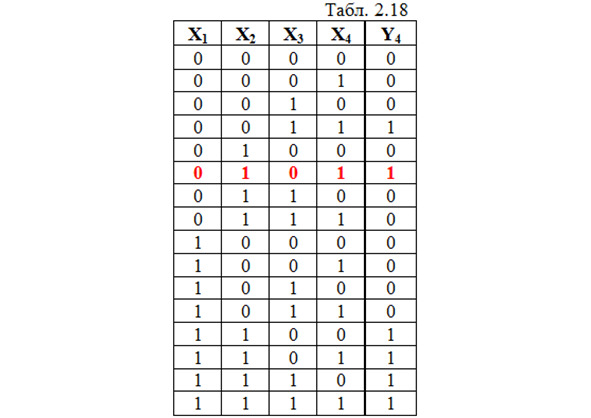
1. Записываем СДНФ:

Y4 = X1′·X2′·X3·X4 \/ X1′·X2·X3′·X4 \/ X1·X2·X3′·X4′ \/

\/ X1·X2·X3′·X4 \/ X1·X2·X3·X4′ \/ X1·X2·X3·X4.

2. Минимизируем СДНФ методом Вейча (рис. 2.41):

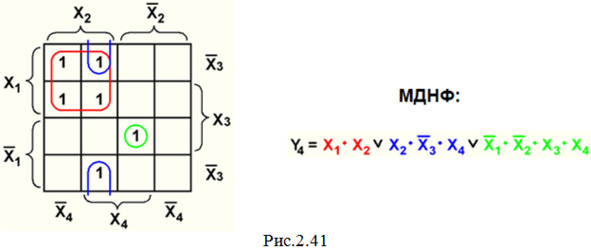
3. Подсчитываем требуемое количество элементов: 3 элемента НЕ +1 элемент 2И +1 элемент 3И +1 элемент 4И +2 элемента 2ИЛИ.

4. Подбираем микросхемы: по одной микросхеме КР1533ЛН1, КР1533ЛИ1, КР1533ЛИ3, КР1533ЛИ6, КР1533ЛЛ1.

5. Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис. 2.42) и выполняем анализ ее работы в статическом режиме для одной комбинации входных сигналов (см. красную строку в табл. 2.18).

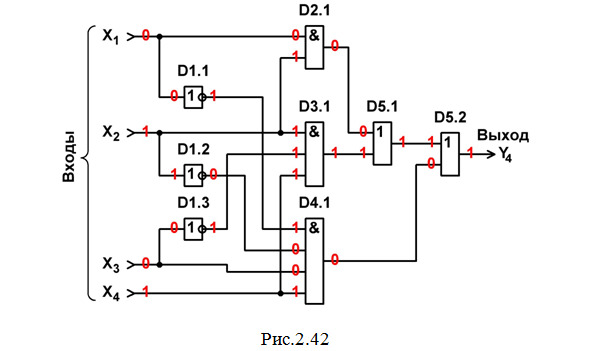
6. Составляем перечень элементов к этой схеме (табл. 2.19).

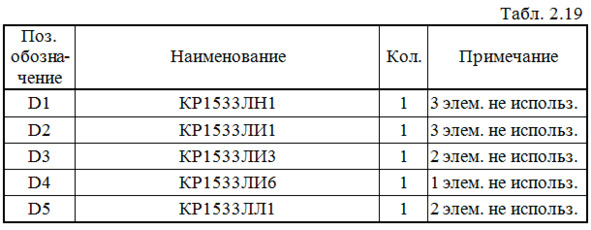
7. Определяем аппаратурные затраты и задержку:

W = 3/6 +1/4 +1/3 +1/2 +2/4 = 0,5 +0,25 +0,33 +0,5 +

+0,5 = 2,08 корпуса; T = 4τ.

8. Переходим к базису И-НЕ:

Y4 = [X1·X2 \/ X2·X3′·X4 \/ X1′·X2′·X3·X4]′′ =

= [(X1·X2)′· (X2·X3′·X4)′· (X1′·X2′·X3·X4)′]′ =

= [(X1 / X2) / (X2 / X3′ / X4) / (X1′ / X2′ / X3 / X4)].

9. Подсчитываем требуемое количество элементов: 4 элемента 2И-НЕ (из них 3 элемента – для отрицания Х1, Х2 и Х3) +2 элемента 3И-НЕ +1 элемент 4И-НЕ.

10. Подбираем микросхемы: по одной микросхеме КР1533ЛА3, КР1533ЛА4 и КР1533ЛА1.

11. Строим схему ЦУ в базисе И-НЕ (рис. 2.43) и выполняем анализ ее работы в статическом режиме для одной комбинации входных сигналов та (см. красную строку в табл. 2.18).

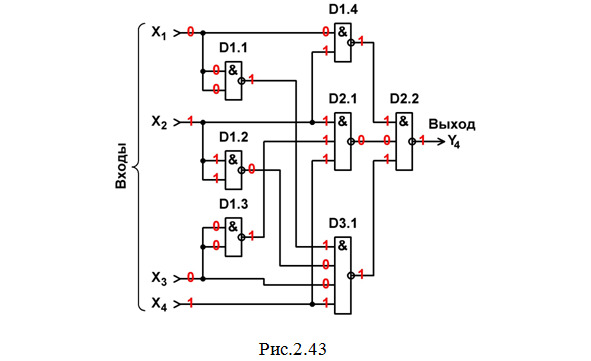
12. Составляем перечень элементов к этой схеме (табл. 2.20).

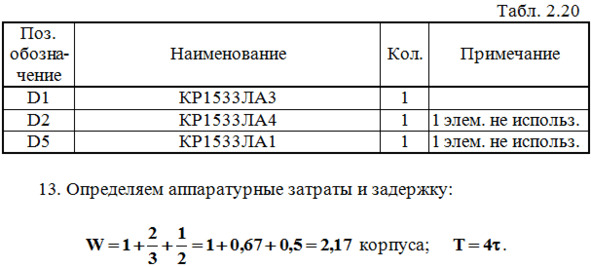
14. Записываем СКНФ:

Y4 = (X1 \/ X2 \/ X3 \/ X4) · (X1 \/ X2 \/ X3 \/ X4′) ·

· (X1 \/ X2 \/ X3′ \/ X4) · (X1 \/ X2′ \/ X3 \/ X4) ·

· (X1 \/ X2′ \/ X3′ \/ X4) · (X1 \/ X2′ \/ X3′ \/ X4′) ·

· (X1′ \/ X2 \/ X3 \/ X4) · (X1′ \/ X2 \/ X3 \/ X4′) ·

· (X1′ \/ X2 \/ X3′ \/ X4) · (X1′ \/ X2 \/ X3′ \/ X4′).

15. Минимизируем СКНФ методом Вейча (рис. 2.44).

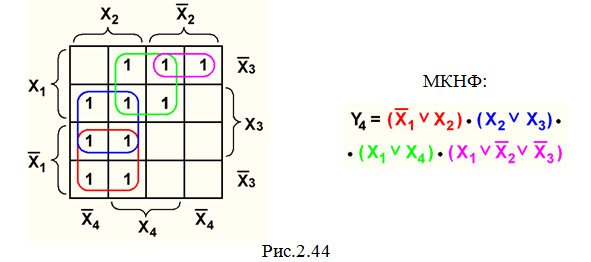
16. Подсчитываем требуемое количество элементов: 3 элемента НЕ +5 элементов 2ИЛИ +1 элемент 4И.

17. Подбираем микросхемы: одна микросхема КР1533ЛН1, две микросхемы КР1533ЛЛ1 и одна микросхема КР1533ЛИ6.

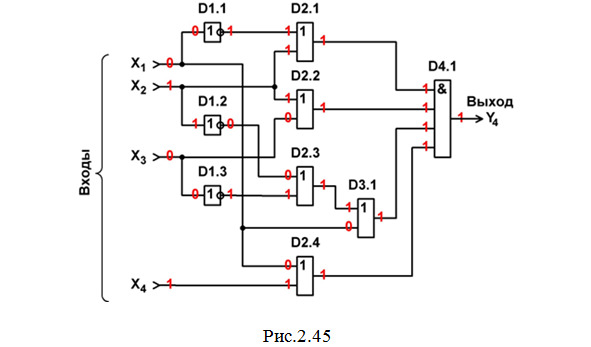
18. Строим схему ЦУ в базисе И, ИЛИ, НЕ (рис. 2.45) и выполняем анализ ее работы в статическом режиме для одной комбинации входных сигналов (см. красную строку в табл. 2.18).

19. Составляем перечень элементов к этой схеме (табл. 2.21).

21. Переходим к базису ИЛИ-НЕ:

Y4 = [(X1′ \/ X2) · (X1 \/ X4) · (X2 \/ X3) · (X1 \/ X2′ \/ X3′)]′′ =

= [(X1′ \/ X2)′ \/ (X1 \/ X4)′ \/ (X2 \/ X3)′ \/ (X1 \/ X2′ \/ X3′)′]′ =

= (X1′ ↓ X2) ↓ (X1 ↓ X4) ↓ (X2 ↓ X3) ↓ (X1 ↓ X2′ ↓ X3′).

22. Подсчитываем требуемое количество элементов: 5 элементов 2ИЛИ-НЕ (из них 3 элемента – для отрицания Х1, Х2 и Х3) +1 элемент 3ИЛИ-НЕ +1 элемент 4ИЛИ-НЕ.

23. Подбираем микросхемы. Здесь предварительно следует обратить внимание на один очень важный момент. Мы только что определили, что в данном случае для построения схемы потребуется элемент 4ИЛИ-НЕ. Но в серии КР1533 нет микросхем, содержащих такие элементы. Как быть? В этом случае берут элементы с большим количеством входов. Но ведь при этом один или несколько входов элемента оказываются лишними, как поступать с ними? С этого момента следует запомнить: неиспользуемые входы логических элементов и вообще любых ЦУ ни в коем случае нельзя оставлять свободными, их обязательно нужно куда-либо присоединять (за редчайшим исключением). Куда – это зависит от функции данного входа в конкретном элементе или ЦУ. Теоретически у элементов И и И-НЕ лишние входы лучше всего подключать к источнику сигнала логической 1 (см. тему 2.9), у элементов ИЛИ и ИЛИ-НЕ – к источнику сигнала логического 0 (см. тему 2.9). Но практически лишние входы любого логического элемента обычно подключаются к любым другим используемым входам этого же элемента.

Именно поэтому в нашей схеме вместо элемента 4ИЛИ-НЕ приходится использовать элемент 5ИЛИ-НЕ из микросхемы КР531ЛЕ7 той же структуры ТТЛШ, которую имеют микросхемы серии КР1533 (в схеме – D4.1), у которого лишний вход подключен к соседнему. Кроме этого, нам потребуются две микросхемы КР1533ЛЕ1 и одна микросхема КР1533ЛЕ4.

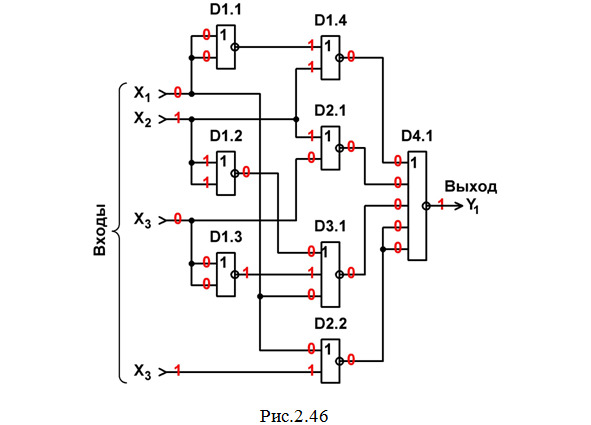
24. Строим схему ЦУ в базисе ИЛИ-НЕ (рис.2.46) и выполняем анализ ее работы в статическом режиме для одной комбинации входных сигналов (см. красную строку в табл. 2.18).

25. Составляем перечень элементов к этой схеме (табл. 2.22).

27. Оценим качество всех четырех схем:

– исключаем схему в базисе ИЛИ-НЕ (рис.2.48), у которой наибольшие аппаратурные затраты W = 2,33

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Примечания

1

***Темы, отмеченные звездочками, не были включены в программу предмета ко времени работы над книгой из-за недостатка времени по учебным планам. Они здесь даются для расширения и углубления знаний тех учащихся, которым это интересно, а также для помощи при выполнении курсовых работ и дипломных проектов.