Цифровые устройства. Учебник для колледжей

Для примера можно привести микросхему КР1533ЛП8 (рис.1.22).

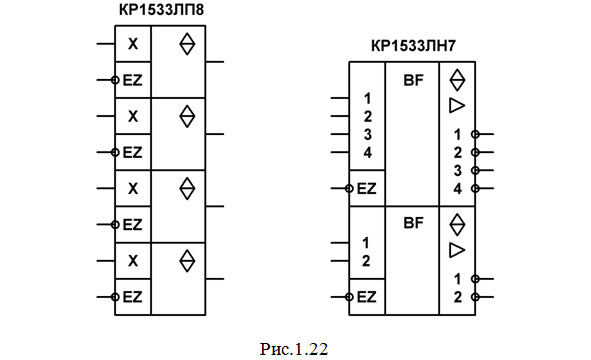
Она содержит 4 буферных повторителя, каждый из которых имеет управляющий состояниями вход EZ (E – enable – давать возможность, разрешать). При установке логического 0 на входе EZ элементу разрешается работать в качестве обычного повторителя, а если на этот вход подать сигнал 1, то элемент переходит в Z-состояние и его выход размыкается (состояние разомкнутого выхода принято обозначать: Z или Roff). Управляющий состояниями вход иногда называют разрешением по выходу и обозначают ЕО (Е – enable, O – output).

В некоторых случаях вход EZ делается общим для нескольких элементов. Например, в микросхеме КР1533ЛН7 (рис.1.22) содержится шесть буферных элементов НЕ с тремя состояниями выходов и повышенной нагрузочной способностью, разделенных на две группы по 4 и 2 элемента. Каждая группа элементов имеет свой управляющий состояниями вход EZ. Подача сигнала 1 на такой вход переводит в Z-состояние сразу все элементы соответствующей группы.

Подобные микросхемы, содержащие объединенные в группы элементы НЕ или повторители с тремя состояниями, которые имеют еще и повышенную нагрузочную способность, называют шинными формирователями или магистральными приемопередатчиками.

П р и м е ч а н и е. Часть линий, сгруппированных по функциональному назначению, называется шиной. Например, информационная шина, по всем линиям которой передается информация; шина управления, по линиям которой передаются сигналы управления; и т. д. Совокупность шин называется магистралью.

У таких ИМС в третьей части маркировки обычно ставят буквы АП, хотя иногда используется маркировка ЛП или ЛН (как, например, в только что рассмотренной микросхеме). Условное графическое изображение формирователей имеет, как правило, буквы BF (от английского buffer – буфер). Применяются они обычно в микропроцессорных системах и системах обработки данных с магистральной организацией обмена информацией.

Можно привести еще один пример шинного формирователя: КР1533АП4 (рис.1.23). Данная ИМС содержит два четырехразрядных магистральных передатчика, каждый из которых имеет по четыре буферных повторителя с тремя состояниями и повышенным коэффициентом разветвления.

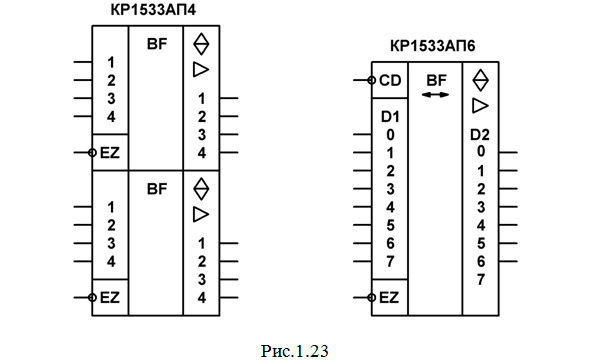
Некоторые формирователи могут передавать информацию в обоих направлениях. Например, восьмиразрядный двунаправленный приемопередатчик КР1533АП6 (рис.1.23) содержит 8 буферных повторителя с тремя состояниями и повышенной нагрузочной способностью, у которых изменение направления передачи информации производится с помощью сигнала на дополнительном входе CD: при CD = 1 передача информации производится от D1 к D2, при CD = 0 – наоборот.

***1.10. Мажоритарные элементы

Мажоритарный (от английского majority – большинство) элемент формирует на своем выходе такой сигнал, который действует на большинстве его входов.

В качестве примера можно рассмотреть микросхему КР1533ЛП3 (рис.1.24). Она содержит три мажоритарных элемента «два из трех» (т.е. на выходе формируется такой сигнал, который действует не менее чем на двух входах из трех), работа каждого из них описывается таблицей истинности (табл.1.5).

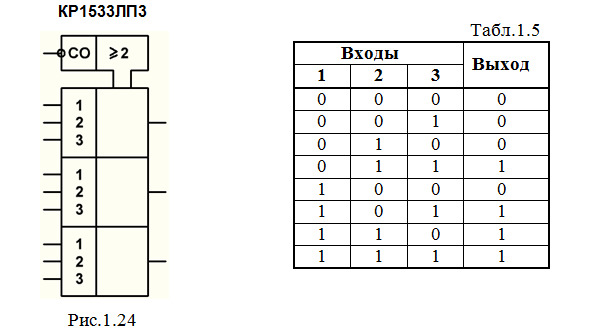
ИМС имеет общий для трех элементов управляющий вход СО, на котором для нормальной работы должен поддерживаться уровень логического 0. При СО = 1 значение выходного сигнала определяется только сигналом на входе 3.1

1.11. Преобразователи уровней

При использовании в аппаратуре микросхем различной структуры возникает необходимость их согласования по таким важнейшим параметрам, как уровни сигналов и потребляемая мощность.

Эту задачу решают специальные ИМС, которые получили название: преобразователи уровней логических сигналов.

Микросхемы любых преобразователей в третьей группе маркировки имеют первую букву П, а вторая буква указывает на конкретный вид преобразователя. Для ИМС преобразователей уровней принято обозначение: ПУ.

Для примера рассмотрим микросхему К564ПУ9 (рис.1.25).

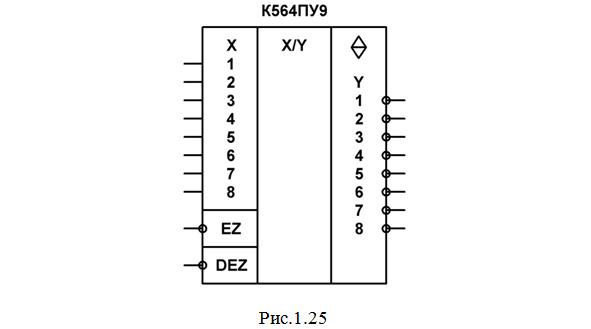
Она может выполнять одновременное преобразование 8 сигналов как от уровня ТТЛ (ТТЛШ) к МОП, так и от уровня МОП к ТТЛ (ТТЛШ). Входы ЕZ и DEZ предназначены для управления режимами работы:

– при подаче на вход DEZ сигнала 0 микросхема выполняет преобразование сигналов МОП уровня в ТТЛ (ТТЛШ) при любом сигнале на входе EZ;

– при одновременной установке сигналов 1 на входах EZ и DEZ микросхема выполняет преобразование сигналов ТТЛ (ТТЛШ) уровня в МОП;

– если же на входе EZ установить уровень логического 0, а на вход DEZ подать 1, то микросхема переходит в Z-состояние.

Следует учесть, что выходные сигналы инвертируются, т.к. на выходах стоит графический знак операции логического отрицания.

П р и м е ч а н и е. В настоящее время выпускаются микросхемы МОП-структуры, прямо совместимые со стандартными сериями ТТЛ (ТТЛШ). Например, микросхемы серий 1564, КР1564, КР1594 (аналоги – соответственно серии ММ54НС, ММ74НС и 74АСТ фирмы «National Semiconductor»).

Раздел 2. Основы синтеза и анализа работы цифровых устройств

Целью тем, изложенных в разделе 2, является овладение учащимися основам синтеза (разработки структуры и построения схем) ЦУ с помощью логических элементов и анализа (проверки правильности) их работы.

2.1. Формы записи логических функций

Предположим, задана таблица истинности (табл.2.1 на рис.2.1), описывающая работу ЦУ, которое имеет три входа Х1, Х2, Х3 и один выход Y1.

Цель: с помощью логических элементов построить схему, которая будет работать так, как указано в этой таблице.

Первым этапом работы является запись зависимости выходной логической функции (значений сигнала на выходе) Y1 от значений логических переменных Х1, Х2, Х3 (значений сигналов на входах) в базисе И, ИЛИ, НЕ (т.е. с использованием операций логического умножения, сложения и отрицания). Такая запись может выполняться в двух формах:

1. СДНФ (совершенная дизъюнктивная нормальная форма) представляет собой несколько многочленов (минтермов), объединенных операцией логического сложения (дизъюнкции), почему форма и названа дизъюнктивной. Она составляется для значений функции Y, равных 1, количество которых и определяет число многочленов. Каждый многочлен представляет собой логическое умножение всех переменных (в данном случае – трех переменных Х1, Х2, Х3), причем для нулевого значения любой переменной следует брать ее инверсию.

Запишем СДНФ для заданной в табл.2.1 логической функции Y1 на рис.2.1.

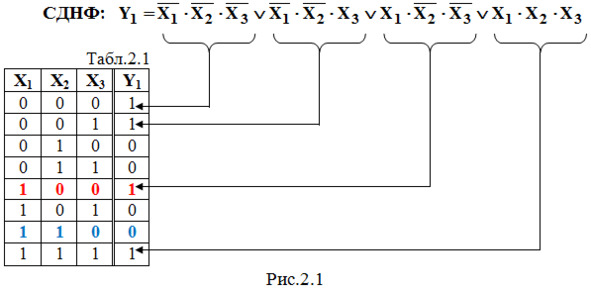
Приведем еще два примера составления СДНФ для логических функций Y2 и Y3, заданных в табл.2.2 на рис.2.2.

2. СКНФ (совершенная конъюнктивная нормальная форма) представляет собой несколько многочленов (минтермов), объединенных операцией логического умножения (конъюнкции), почему форма и названа конъюнктивной. Она составляется для значений функции Y, равных 0, количество которых и определяет число многочленов. Каждый многочлен представляет собой логическое сложение всех переменных (в данном случае – трех переменных Х1, Х2, Х3), причем для значения любой переменной X = 1 следует брать ее инверсию.

Запишем СКНФ для заданной в табл.2.1 логической функции Y1 (на рис.2.3).

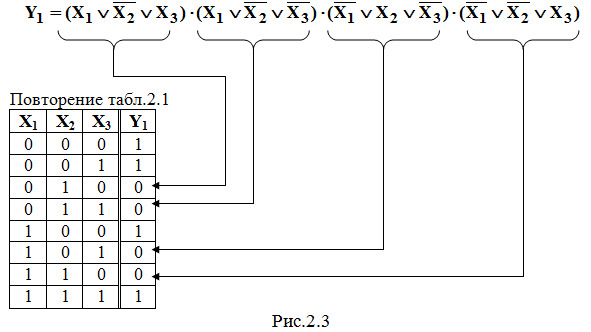
П р и м е ч а н и е:

Символом операции НЕ (инвертирования) обычно является черточка над буквой, как показано в табл.1.1. Именно такой символ мы применяли при записи СДНФ для функций Y1, Y2, Y3 и СКНФ для функции Y1. Но довольно часто, особенно на рисунках карт Вейча (Карно) и в изображениях микросхем, используется другой символ инвертирования – апостроф рядом с буквой: Y = X′. Как уже упоминалось во Введении, при выполнении лабораторных работ, а также в демонстрационных материалах применяется компьютерная программа исследования работы элементов и устройств цифровой микроэлектроники Electronics Workbench, где для изображения инверсных выводов как раз употребляется второй вариант символа инвертирования. Поэтому в дальнейшем для привыкания мы будем практиковать оба варианта символа инвертирования.

Приведем еще два примера записи СКНФ для функций Y2 и Y3, заданных в табл.2.2, где будем использовать два варианта записи символа инвертирования (рис.2.4):

В дальнейшем мы будем применять апостроф преимущественно в текстовом материале и формулах, а черточку над буквами – на рисунках.

2.2. Минимизация логических функций

методом Вейча

Любая совершенная нормальная форма (СДНФ или СКНФ) содержит очень большое количество логических операций, поэтому схемная реализация ЦУ непосредственно по СДНФ (или по СКНФ) потребует соответствующего числа логических элементов, которые должны будут выполнять данные операции. Поэтому невольно напрашивается вопрос: а нельзя ли логические выражения вида СДНФ или СКНФ упростить, чтобы количество операций (и, соответственно, количество элементов в схеме ЦУ) стало меньше? Оказывается, что в подавляющем большинстве случаев это сделать можно!

Процесс упрощения логических выражений любой совершенной нормальной формы записи получил название: минимизация от латинского minimum. Существует несколько способов ручной минимизации, но практически наиболее простым и наглядным является метод Вейча (несколько модифицированный метод Карно), который мы и будем здесь рассматривать. Его единственным недостатком является невозможность применения для минимизации логических выражений, содержащих более чем 5 переменных; но т.к. это случается довольно редко, то с указанным недостатком вполне можно мириться.

Сущность данного метода заключается в применении так называемых карт (диаграмм) Вейча, которые представляют собой прямоугольники, разделенные на клетки (карты Карно несколько отличаются от карт Вейча, но суть метода та же; – смотрите окончание данного параграфа). Количество клеток в карте определяется числом наборов переменных (числом комбинаций входных сигналов) N = 2n, где n – это количество переменных; причем каждой клетке строго соответствует свой набор переменных, определяемый по обычной координатной сетке.

Рассмотрим два наиболее часто встречающихся случая:

1. Для ЦУ с n = 3 входами максимальное число наборов переменных (смотрите таблицы 2.1 и 2.2 таких устройств) равно 2n = 23 = 8, следовательно и карта Вейча будет иметь 8 клеток (рис.2.5):

2. Для ЦУ, имеющего n = 4 входа, максимальное число наборов переменных равно 2n = 24 = 16, поэтому карта Вейча тоже будет иметь 16 клеток (рис.2.6).

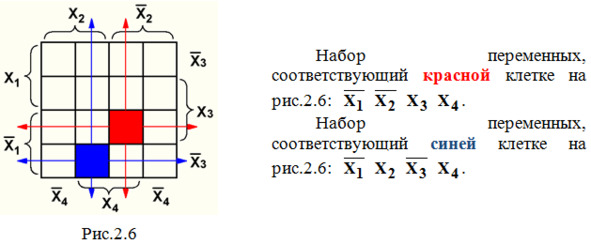
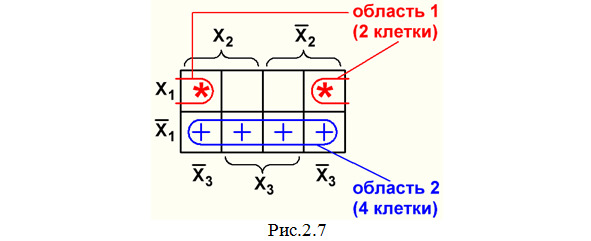
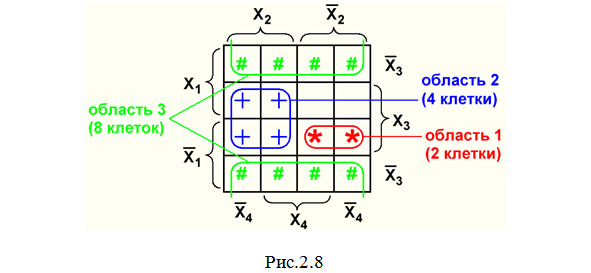
Главной особенностью любой карты Вейча является возможность объединения соседних клеток карты. Области объединения должны быть прямоугольными и содержать 2n (2,4,8,16) клеток. Допускается сворачивать карту в цилиндр с объединением соседних граней; примерами такого объединения являются: область 1 на рис.2.7 и область 3 на рис.2.8. Не допускается включать в объединение пустые клетки.

Рассмотрим примеры объединения клеток.

1. В карте Вейча с 8 клетками (рис.2.7).

2. В карте Вейча с 16 клетками (рис.2.8).

В каждой такой области объединения выполняется операция «склеивания», в результате которой остается только один многочлен только с теми переменными, которые входят во все объединенные клетки. А переменные типа X1 и X1′, X2 и X2′, X3 и X3′, X4 и X4′ «сокращаются». Это можно объяснить на следующем примере: возьмем два многочлена СДНФ (аналогичный результат получается и с многочленами СКНФ), соответствующих двум клеткам области 1 рис.2.7:

Х1·Х2·X3′ \/ X1·X2′·X3′;

одинаковые переменные вынесем за скобки:

X1·X3· (X2 \/ X2′);

легко проверить, что выражение в скобках при любых значениях X2 (0 или 1) дает 1, тогда:

X1·X3·1 = X1·X3.

Итак, в результате «склеивания» двух клеток области 1 рис.2.7 получается: X1·X3.

Приведем примеры (рис.2.10) «склеивания» клеток в карте Вейча на рис.2.4:

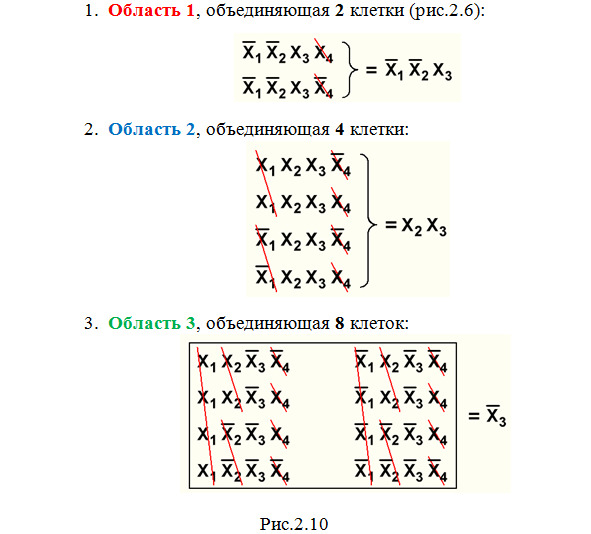
Очевидно, что при объединении всех клеток любой карты сокращаются все переменные, и результат «склеивания» дает 1.

Из сравнения полученных результатов можно сделать вывод: чем больше объединяется клеток, тем проще получается результат «склеивания», т.е. итоговое логическое выражение содержит меньше операций, и, соответственно, схема ЦУ будет иметь меньше логических элементов.

Теперь приведем порядок минимизации:

– Чертим карту Вейча с нужным количеством клеток.

– Клетки карты, соответствующие минтермам СДНФ (или СКНФ) обозначаем символом «1».

– Объединяем все клетки с «1». Количество клеток в каждом объединении должно быть максимальным, а самих областей объединения должно быть как можно меньше. П р и м е ч а н и е: любое количество клеток с «1» могут одновременно входить в две или больше области объединения.

– В каждой области производим операцию «склеивания», в результате чего получаем многочлены минимальной формы: МДНФ или МКНФ.

Приведем несколько примеров минимизации:

Пример 1. Минимизация СДНФ функции Y1 из темы 2.1 (рис.2.11):

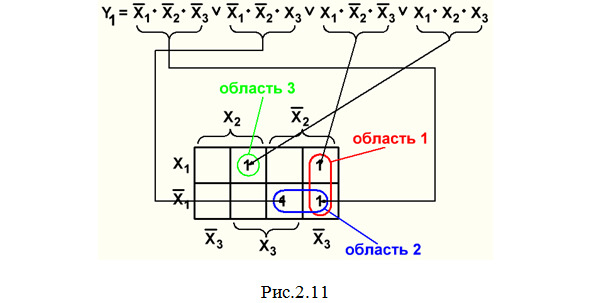
Покажем на рис.2.12 результаты"склеивания» двух клеток в областях 1 и 2 этой карты.

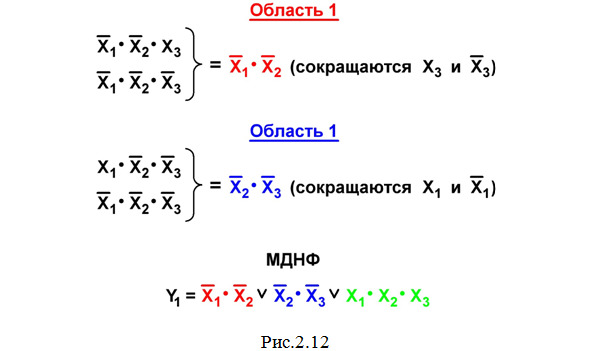
Область 3: Эта клетка остается одна – ни с какими другими клетками, содержащими «1», ее объединить нельзя. Поэтому соответствующий данной клетке многочлен Х1·Х2·Х3 не сокращается и входит в минимальную дизъюнктивную нормальную форму (МДНФ) без изменения.

В результате на этом же рис.2.12 записываем МДНФ (красным, синим и зеленым цветом показаны минтермы, которые получились в результате «склеивания» клеток в областях объединения соответствующего цвета на рис.2.11).

Пример 2. Минимизация СДНФ функции Y2 из темы 2.1 (рис.2.13):

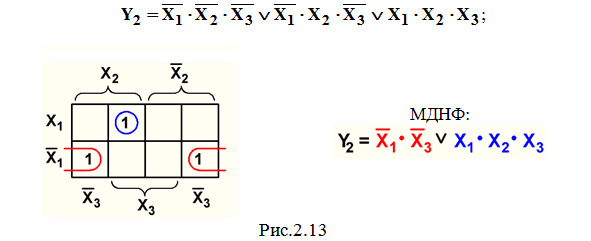
Пример 3. Минимизация СДНФ функции Y3 из темы 2.1 (рис.2.14):

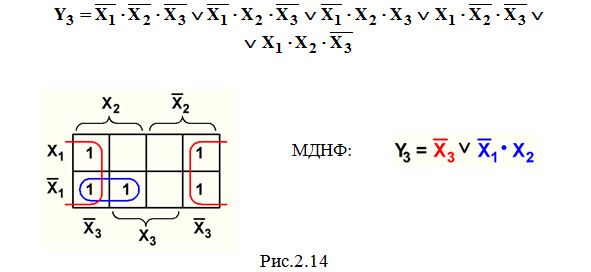
Совершенно аналогично выполняется минимизация логических функций, записанных в СКНФ. Рассмотрим примеры:

Пример 4. Минимизация СКНФ функции Y1 из темы 2.1 (рис.2.15):

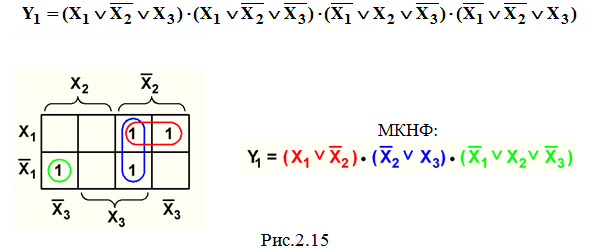
Пример 5. Минимизация СКНФ функции Y2 из темы 2.1 (рис.2.16).

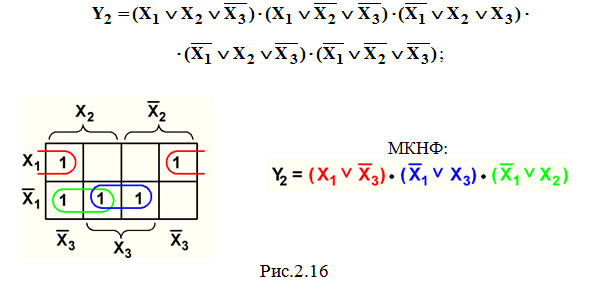
Пример 6. Минимизация СКНФ функции Y3 из темы 2.1 (рис.2.17).

***

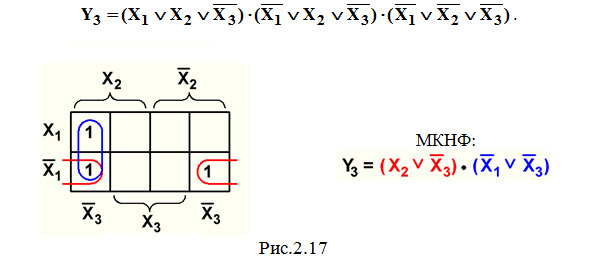
Модификация карт Вейча, предложенная Карно, заключается в небольшом изменении координатной сетки (на рис. 2.18 показаны карты Карно для минимизации функций трех и четырех переменных дизъюнктивной формы).

Основным достоинством карт Карно по сравнению с картами Вейча является возможность их заполнения непосредственно по значениям сигналов в таблице истинности, не записывая СДНФ (или СКНФ). Но если координатная сетка карт Вейча одинаково применима для минимизации функций как дизъюнктивной, так и конъюнктивной форм, то в координатной сетке карт Карно для минимизации функций конъюнктивной формы прямые и инверсные значения переменных меняются местами по сравнению с координатной сеткой карт Карно для минимизации функций дизъюнктивной формы. На рис. 2.18 показано заполнение карт Карно, объединение клеток и результат минимизации функций Y1 (см. табл. 2.1) и Y4 в виде МДНФ.

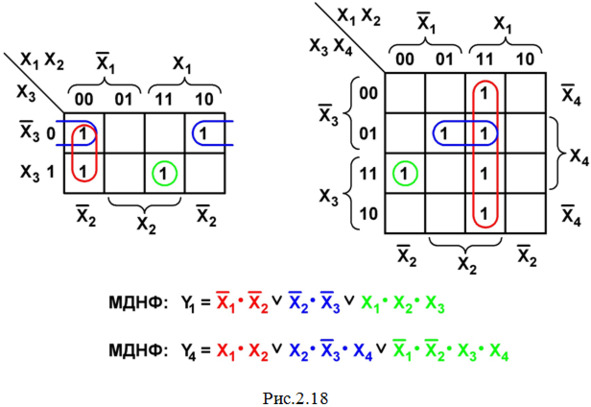
Сравнивая эти результаты с МДНФ примера 1 данной темы и примера из темы 2.8, мы легко убеждаемся, что они полностью совпадают с полученными при использовании карт Вейча.

2.3. Подбор микросхем, построение и анализ работы схем ЦУ в базисе И, ИЛИ, НЕ. Оценка качества схем

Построение схем производится таким образом, чтобы соблюдался порядок выполнения операций в логическом выражении согласно элементарным правилам как обычной алгебры, так и алгебры логики.

Достаточно очевидно, что при построении схем ЦУ по МДНФ порядок выполнения операций должен быть следующим:

– Логическое отрицание входных сигналов Х, то есть первыми в схеме должны стоять элементы НЕ.

– Логическое умножение (элементы И).

– Логическое сложение (элементы ИЛИ).

Пример 1. МДНФ (см. пример 1 из темы 2.2):

Y1 = X1′·X2′ \/ X2′·X3′ \/ X1·X2·X3.

Определяем количество операций (и, соответственно, требуемых логических элементов) для реализации этой МДНФ:

1. В данном логическом выражении стоят 4 знака операции логического отрицания. Но следует учесть, что инвертирование одного и того же сигнала X2 просто встречается два раза. Поэтому схема должна содержать 3 элемента НЕ для отрицания сигналов X1, X2 и X3.

2. Для выполнения первого умножения X1′·X2′ потребуется один элемент 2И, т.к. в этой операции участвуют два сигнала: X1′ и X2′.

3. Для выполнения второго умножения X2′·X3′ также потребуется один элемент 2И.

4. В третьем многочлене X1·X2·X3 требуется умножение трех сигналов, поэтому здесь нужно использовать один элемент 3И.

Таким образом, для выполнения операций умножения мы должны использовать 2 элемента 2И и один элемент 3И.

5. Логическое сложение трех многочленов X1′·X2′; X2′·X3′ и X1·X2·X3 требует применения одного элемента 3ИЛИ. Но нужно сразу учесть, что в серии КР1533 и во многих других нет микросхем, содержащих элементы 3ИЛИ. Поэтому для реализации нужного нам сложения придется использовать 2 элемента 2ИЛИ.

По записи МДНФ видно, что именно в такой последовательности нужно выполнять операции: сначала логическое отрицание НЕ, затем логическое умножение И, и в конце логическое сложение ИЛИ.

Подбираем микросхемы. В данном случае для построения схемы достаточно взять:

– Одну микросхему КР1533ЛН1 (см. рис.1.12), содержащую 6 элементов НЕ. Т. к. нам требуется только 3 элемента НЕ, то в данной микросхеме 3 элемента оказываются лишними и использоваться они не будут.

– Одну микросхему КР1533ЛИ1 (см. рис.1.12), содержащую 4 элемента 2И (здесь два элемента оказываются лишними), и одну микросхему КР1533ЛИ3 (см. рис.1.12), содержащую 3 элемента 3И (из нее 2 элемента использоваться не будут).

– Одну микросхему КР1533ЛЛ1 (см. рис.1.13), содержащую 4 элемента 2ИЛИ (два элемента этой микросхемы оказываются лишними).

Строим схему ЦУ в базисе И, ИЛИ, НЕ (термин «базис И, ИЛИ, НЕ» означает, что в данной схеме будут использоваться только элементы И, ИЛИ, НЕ), причем операции должны производиться в установленной нами последовательности: сначала НЕ, затем И, и в конце ИЛИ. Обращаем внимание, что при необходимости указывать направление передачи сигналов входы и выходы могут быть начерчены не кружочками (как в Разделе 1), а стрелками.