Взыскующие знания

«Обучая математике, – продолжает свой рассказ хронист, – он начинал с арифметики, которая является первой частью этой науки». По складу мышления Рихер был, по-видимому, гуманитарием, и поэтому ограничился лишь одним абзацем, рассказывая о том, как Герберт учил своих слушателей умножать и делить многозначные числа на абаке. Впрочем, мог ли он представить, что именно этот инструмент и правила счета на нем обеспечат Герберту известность и славу в грядущих поколениях и что через тысячу лет уровень цивилизации в значительной степени будет определяться электронными наследниками абака?

Происхождение термина «абак» в точности не установлено. Большинство историков производят его от семитского корня; согласно этому толкованию абак – это дощечка, покрытая слоем пыли. На ней острой палочкой проводились линии и какие-нибудь предметы, например, камешки или палочки, размещались в получившихся колонках по позиционному принципу. Сложение и вычитание на абаке выполнялись добавлением или изъятием камешков, умножение и деление – как повторные сложения и вычитания соответственно.

С абаком были знакомы в древности и египтяне, и греки, и римляне. Историки полагают, что, например, в Грецию абак был завезен финикийцами и стал там «походным инструментом» греческих купцов. Значения, приписываемые камешкам в колонках, обычно сообразовывались с соотношениями различных денежных единиц. Историк Полибий, желая съязвить, писал: «Придворные – как камешки на счетной доске; захочет счетчик, и они будут стоить один халк, а захочет – так и целый талант». В Древнем Риме абак назывался calculi, или abaculi, и изготовлялся из бронзы, камня, слоновой кости и цветного стекла. Слово calculus означает «галька», «голыш». От него произошло позднейшее латинское calculatore (вычислять) и наше калькуляция. Сохранился бронзовый римский абак, на котором calculus передвигались в вертикально прорезанных желобках. Внизу помещали камешки для счета до пяти, а в верхней части имелось отделение для камушка, соответствующего пятерке.

Прошло много веков и вид абака изменился. Рихер рассказывает, как Герберт заказал мастеру, изготовлявшему щиты, кожаную счетную доску, разделенную на двадцать семь колонок, а также велел сделать тысячу жетонов из рога и нанести на каждый из них одну из девяти арабских цифр, от единицы до девяти. Знака нуля Герберт не знал, да он и не нужен был при счете на абаке, так как заменялся пустой колонкой.

Существовал и другой вариант абака, который описал в XI веке ученик Герберта парижанин Бернелэн (рис. 1–4). Это была гладкая доска, посыпанная голубым песком и разделенная на тридцать колонок. Три колонки отводились для дробей, а прочие объединялись по три в девять групп. Сверху колонок были дуги, которые назывались пифагоровыми (arcus Pytagori), так как изобретение абака приписывалось Пифагору. Колонки повторно помечались наверху слева направо буквами C (centum – сто), D (decem – десять) и S или M (латинское singularis или греческое монас – единица). Жетоны с цифрами Бернелэн именовал апексами (от латинского apex, одно из значений которого – письмена). Вскоре к известным апексам добавился еще один жетон – кружок с точкой внутри. Его называли сипос (от греческого псефос – камешек, жетон) и использовали как метку для памяти, передвигая вдоль колонок в процессе счета.

Рихер утверждал, что Герберт выполнял операции на абаке с такой скоростью, что получал результат умножения быстрее, чем произносил его вслух. «Тот, – писал хронист, – кто хотел бы разобраться в этом методе досконально, должен прочитать книгу, которую он написал для схоластика Константина». Сочинение, о котором упоминает Рихер, называлось «Книжечка о делении чисел», схоластик же Константин был другом Герберта и преподавателем школы в монастыре Флери-сюр-Луар. В предисловии к «Книжечке» говорилось: «Сила дружбы делает возможным невозможное. Каким образом у меня могло бы появиться желание объяснить правило чисел абака, если бы я не был к тому побуждаем тобой, о, Константин, сладкая утеха моих трудов. Итак, хотя уже произошло несколько люстров (пятилетий. – Ю. П.) с тех пор, как у меня не было под руками книги по этому предмету или упражнений в нем, я все же оказываюсь в состоянии изложить его, отчасти по памяти, буквально в тех же выражениях [как в книге], отчасти только придерживаясь того же смысла. Пусть же безграмотный философ не думает, что эти правила находятся в противоречии с какой-либо наукой или сами с собой».

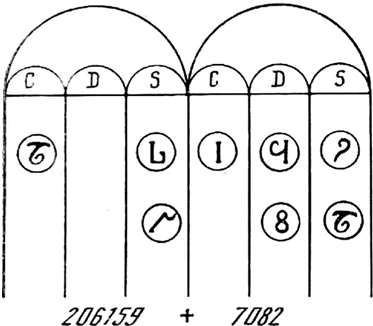
Рис. 1–4. Абак XI века (фрагмент)

Уже из этого отрывка следует, что Герберт не был изобретателем абака, как иногда утверждалось, а лишь восстановил то, что было известно, но пришло в забвение («В Х веке не творят, а зубрят, восстанавливают по памяти» – замечает по этому поводу историк). Заслуга Герберта состоит в популяризации инструментального счета, в использовании индо-арабских цифр[20] на жетонах и (может быть!) в разработке правил умножения и деления на абаке. Эти операции выполнить письменно весьма сложно, если пользоваться римской системой счисления (попробуйте, например, перемножить СХIХ и ХХIV). На абаке же умножение выполнялось значительно проще.

Пусть, скажем, требуется 4600 × 23. Ход вычислений следующий: 3 × 6=18; 3 × 4=12; 2 × 6=12; 2 × 4=8; 1+2+2=5; уничтожим цифры 1, 2, 2 и напишем 5;1+1+8=10; в следующей колонке слева напишем 1. Таким образом, получается сумма 105800. При вычислении на абаке вычеркиванию цифр соответствовало удаление жетонов (например, жетоны 1, 2, 2 заменялись жетоном с цифрой 5). Выполнение деления на абаке значительно сложнее. Герберт использовал прием, при котором деление на какое-либо число b заменялось более простым делением на близкое к нему «круглое» число c, что требовало после каждой операции вспомогательного умножения на разность или дополнение c-b (или b-c) и сложения, причем делимое разбивалось всякий раз на отдельные разряды.

Конечно же, столь громоздкое правило представлялось современникам Герберта верхом изобретательности. Недаром молва обвиняла его в связи с дьяволом также и из-за умения делить на абаке большие числа, а знакомый нам отец Уильям из Малмсбери уничижительно писал: «Герберт был, несомненно, первым, кто перенял у сарацинов абак. Он написал о нем правила такого рода, что абацисты, сколько бы ни старались, постигают их с трудом». Другого мнения придерживался преподаватель известной монастырской школы в Лане монах Радульф (ум. 1131): «От Герберта, человека высочайшего благоразумия, одно имя которого означает мудрость, от известного ученого Германа[21] и их учеников поток знаний об абаке достиг нашего времени».

О популярности Герберта в Средние века свидетельствует то обстоятельство, что иногда вместо слова «абацист», то есть вычислитель на абаке, говорили «герберкист» – последователь Герберта. Через несколько веков Леонардо Пизанский (ок. 1170–1250), прозванный Фибоначчи[22], в своей «Книге абака» называл счет на абаке Герберта одним из трех существовавших способов вычислений (два других способа – счет на пальцах и modus Indorum – письменные вычисления с помощью индо-арабских цифр). Последний способ после выхода книги Леонардо постепенно завоевал популярность, чему немало способствовало проникновение и распространение в Европе бумаги. В течение следующих двух-трех столетий развернулась острая борьба между «абакистами», отстаивавшими использование абака и римской системы счисления, и «алгоритмиками», отдававшими предпочтение индо-арабским цифрам и письменным вычислениям. Борьба эта завершилась победой «алгоритмиков» лишь в XVII веке.

Но вернемся к рассказу Рихера. «После арифметики он переходил к музыке, в которой галлы долгое время были невежественны и которую он сделал очень популярной. Определяя высоту тона струн с помощью монохорда[23] и разделяя консонансы на тоны, полутоны и даже на трети и четверти тона… он восстановил совершенное знание музыки». Трудно предположить, однако, чтобы в теоретических вопросах Герберт пошел дальше Боэция, который в «Наставлениях к музыке» говорит об арифметических отношениях октавы (1:2), кварты (3:4), квинты (2:3), полутона (243:256), большого полутона (aptome) к малому (limma vel dieses) (139:104), о комме – разнице между целой октавой и совокупностью кварты и квинты и так далее. Отсутствие гаммы, изобретенной полувеком позднее бенедиктинским монахом Гвидо из Ареццо[24] (ок. 990–ок.1050), в значительной степени затрудняло понимание этой отвлеченной теории музыки, и поэтому лишь Герберт с его знанием математики смог просветить «невежественных галлов». Впрочем, Рихер говорит, что сам он и архидьякон Геранн отказались от изучения этого искусства («ввиду крайней его сложности»).

Рихер ничего не сообщает о характере преподавания Гербертом геометрии, но о познаниях caput scholae можно судить по его незавершенной книге «Геометрия» и письму монаху Адельбольду из Утрехта. В теоретическом отношении книга Герберта представляла собой компиляцию из сочинений Боэция и Евклида. Но «Начала» великого грека были известны тогда латинской Европе лишь фрагментарно, а ни греческого, ни арабского языков Герберт не знал. Поэтому в «Геометрии» он привел только формулировки Евклидовых теорем и доказательства трех из них. Проявляя некоторый критический дух, в целом отсутствующий в этом сочинении, он указывал, что в действительности ни одна точка, ни одна линия и поверхность не встречаются иначе, чем в связи с каким-нибудь телом, и лишь мысленно мы отрываем точки, линии и поверхности от этих тел.

Практическая часть книги посвящена приемам римских агрименсоров (землемеров). Герберт пишет об измерении длин, площадей и объемов различных геометрических фигур. Он показывает, как с помощью астролябии, стрелы с привязанной ниткой и измерения тени можно вычислить площади фигур разной формы; определяет число зданий, которые можно разместить на этой площади; измеряет высоту доступных и недоступных объектов (башен, церквей, гор), узнает ширину реки, глубину колодца и так далее.

Для вычисления площади равностороннего треугольника (важнейшая задача при проведении землеустройства) он рекомендует принимать его высоту равной 6/7 стороны, что весьма близко к правильному значению (√3/2). «Пусть будет тебе известно общее правило для нахождения высоты, в равностороннем треугольнике, – пишет Герберт Адельбольду: отнимай всегда от стороны седьмую часть и шесть остальных считай за высоту. Но чтобы ты лучше понял, о чем идет речь, возьмем пример… Дан тебе треугольник, сторона которого равна 7 футам длины; по геометрическому правилу я его [площадь] измеряю так: отнимаю от стороны седьмую часть и, принимая остальные 6/7 за перпендикуляр, умножаю его на сторону и говорю: 6х7=42; половина этого числа 21 и есть площадь означенного треугольника». Далее Герберт разъясняет своему корреспонденту ошибку агрименсоров, которые измеряют площадь квадратами и не принимают при этом в расчет тех отрезков этих фигур, которые оставались вне измеряемой площади («поэтому вместо числа 21 они получали в ответе неверное число 28»).

Критически оценивая оригинальность математических трудов Герберта, историки науки соглашаются с тем, что его «Геометрия» и письмо Адельбольду – первые геометрические достижения бедной математической культуры Средневековья.

Излагая последний предмет квадривия – астрономию, Герберт использовал наглядные (как мы бы сказали сегодня) пособия, что было, конечно, неслыханным новшеством в педагогической практике Х века. Рихер довольно туманно и, видимо, не до конца понимая[25], описал астрономические инструменты Герберта. Но если соединить сообщаемые им сведения с теми, что содержатся в письме Герберта к уже знакомому нам схоластику Константину, можно в общих чертах представить себе устройство и принцип действия астрономических инструментов, которые использовались в реймской школе.

Чтобы познакомить учеников со звездной картой и научить их распознавать созвездия и отдельные звезды, Герберт изготовил деревянную сферу диаметром около трех футов. На ней он провел две окружности так, чтобы их плоскости были взаимно перпендикулярны. Точки пересечения этих окружностей он определил как Северный и Южный полюсы Мира. Затем с помощью циркуля разделил полуокружность от одного полюса до другого на тридцать частей и начертил на сфере пять параллельных кругов. Первый находился на расстоянии шести частей от Северного полюса (арктический круг); далее через пять частей была расположена линия тропика Рака, и затем через четыре части – линия небесного экватора. Оставшееся расстояние до Южного полюса он разметил параллелями аналогичным образом. По одной из взаимно перпендикулярных окружностей он разделил сферу на две полусферы и выдолбил одну из них, получив таким образом плоскую полусферическую оболочку. В местах пересечения другой окружности с каждой из пяти параллелей, а также в полюсах установил по диоптре[26] длиной в полфута. Чтобы сделать всю конструкцию жесткой, он вставил концы диоптр в отверстия, просверленные в железном полукольце, которое крепилось к основанию инструмента.

Перед началом наблюдений Герберт устанавливал инструмент так, чтобы верхняя диоптра была наведена на Полярную звезду, казавшуюся всю ночь неподвижной. Затем ученики вели наблюдения через другие диоптры за звездами, отмечая пути их движения по небосводу. Днем они сравнивали полученные сведения с теми, что содержались в астрономических рукописях, и наносили на учебные небесные глобусы отдельные звезды и контуры созвездий, раскрашивая их в различные цвета. Сверить свои результаты они могли по большому глобусу, собственноручно изготовленному учителем и установленному так, чтобы ось мира, соединявшая Северный и Южный полюсы, была наклонена на угол, соответствующий широте места (49° для Реймса). Заметим, что, поскольку Герберт делил полуокружность не на сто восемьдесят, а на тридцать частей, каждой из этих частей соответствовали 6 градусам. Поэтому Полярный круг у Герберта находился на отметке 26°, а не 23°8», но линия тропика Рака была расположена достаточно точно.

Второй астрономический инструмент Герберта – армиллярная сфера (от лат. armilla – браслет, кольцо) была известна уже греческому астроному и математику Эратосфену Киренскому (276–194 до н. э.) и великому греческому полимату Клавдию Птолемею (ок.87–165), а также средневековым арабским ученым. Она применялась для определения экваториальных или эклиптических координат небесных светил и состояла из нескольких деревянных колец с делениями, снабженных диоптрами и способных поворачиваться вокруг своей центральной точки. Герберт дополнил инструмент Птолемея еще одним кольцом, расположенным наклонно поперек сферы. На нем были нанесены знаки Зодиака. Над сферой он поместил изготовленные из железной и медной проволоки контуры созвездий и снабдил ее диоптрами, чтобы наблюдать за изменениями положения полярной звезды. «Эта машина, – пишет Рихер, – была столь чудесна, что даже тот, кто был невежествен в науке, но знал местоположение хотя бы одного созвездия на сфере, мог найти другие самостоятельно, без помощи учителя». Позднее, уже будучи римским папою, Герберт сконструировал и изготовил новую армиллярную сферу, основываясь на астрономических таблицах великого арабского ученого Абу-л-Хасан Али ибн Аби Саид Абд-ар-Рахман ибн Юнис ал-Садафи ал-Мисри (950–1009).

Конструируя планетарий, представлявший собой действующего модель движения планет, Герберт черпал необходимые сведения из «Естественной истории» римского эрудита Плиния Старшего (23–79 н. э.) и комментариев римского философа и писателя Амвросия Феодосия Макробия (IV век н. э.) к платоновскому «Тимею». Основой планетария была армиллярная сфера, которую Герберт дополнил главной осью и кольцами, соответствующими пяти параллелям его небесного глобуса. Утолщение в центре главной оси представляло собой неподвижную Землю, остальные планеты «моделировались» металлическими шариками, подвешенными на тонких нитях. Они могли вручную перемещаться по своим орбитам, которые Герберт представил изогнутыми и прикрепленными к главной оси проволочками. Расстояние от Земли до Луны он принял за единицу, а остальные планеты расположил соответственно платоновскому закону совершенных числовых отношений (1:2,3,4,8,9,27). Вся конструкция могла поворачиваться вокруг главной оси, устанавливаемой вертикально. Демонстрируя движение планет, Герберт вращал планетарий, в то время как один из его учеников перемещал «планеты» по их орбитам.

С именем Герберта связано отчасти распространение в Средневековой Европе очень популярного впоследствии прибора – планисферной астролябии, предназначенного, в основном, для решения различных астрономических задач (измерения положений небесных тел, определения времен восхода и захода светил, определения времени суток по наблюдениям высот Солнца или звезд и так далее)[27]. Астролябия была известна многим древнегреческим ученым (Гиппарху, Птолемею и другим), ее описали и усовершенствовали арабские ученые ал-Фазари (Абу Исхак Ибрахим ибн Хабиб ибн Сулейман ибн Самура ибн Джундаб ал-Фазари, ум. ок. 800), Ал-Бируни (Абу-р-Райхан Мухаммед ибн Ахмед ал-Бируни) и другие. Первое описание астролябии на латинском языке появилась в переводе с арабского анонимной книги «Суждения об астрологии». Перевод принадлежал Лупитусу, старому другу Герберта, которому он писал в 984 году: «Хотя у меня нет перед тобой никаких заслуг, твое великодушие и твоя приветливость побудили меня обратиться к тебе с просьбой. Итак, прошу, перешли мне переведенную тобой книгу об астрологии[28], а если захочешь от меня что-либо в вознаграждение, проси без колебаний и получишь». Лупитус не замедлил прислать книгу, а содержавшиеся в ней сведения об астролябии Герберт переработал и включил в «Геометрию». Через полвека на основе этой книги Герман Калека[29] написал трактат об астролябии, пользовавшийся большой популярностью в Европе.

Практическому гению Герберта Европа обязана созданием одного из первых в Средние века гидравлического органа. Если верить Рихеру, Гербертов орган, находившийся одно время в Реймском соборе, был устроен так: пар от кипящей воды наполнял медный барабан и затем вырывался через многочисленные медные трубки с отверстиями, которые в определенной последовательности перекрывались клапанами. Таким образом, нагнетание воздуха в трубы совершалось при помощи механизма, а не выбивающегося из сил церковного служки, и расстояние, на котором был слышен звук, значительно увеличивалось. Остается лишь гадать, явился ли этот музыкальный инструмент оригинальным изобретением Герберта, так как подобного рода органы были известны с античных времен: их описали в своих сочинениях Ктесибий, Филон Византийский и Герон Александрийский[30]. Но наш герой не знал греческого языка, а написанная около 850 года несколькими арабскими авторами «Книга хитроумных приборов», в которой подробно говорилось об органе, была переведена лишь в XIII веке.

И еще об одном изобретении Герберта следует упомянуть: каноник Титмар из Мерзебурга в своей «Хронике» утверждал, что Герберт изготовил и установил в Магдебурге часы (horologium), ничего не сообщая об их конструкции. На основании этого упоминания некоторые позднейшие авторы заявляли, что это были механические башенные часы. Сейчас же считается, что первые часы такого рода были построены лишь в XIV веке, а horologium, скорее всего, представлял собой солнечные часы или клепсидру (водяные часы).

Нетрудно представить, каким чудом казались современникам Герберта его изобретения (прежде всего, астрономические) и как восхищались они его эрудицией! И это восхищение невольно плодило одну легенду за другой. Так, многие средневековые хронисты утверждали, что он не то сконструировал, не то где-то приобрел говорящую бронзовую голову, которая давала ему советы, отвечая на вопросы в режиме дихотомии (пользуюсь современным термином), то есть в режиме «да»/«нет». Впрочем, владение «медным оракулом» приписывалось и некоторым другим выдающимся мыслителям позднего Средневековья, в частности, Роджеру Бэкону, Альберту Великому, Роберту Гроссетесту, Арнольдо из Виллановы.

Герберта, несомненно, можно считать самым выдающимся педагогом Х века. Он преподавал по определенному четкому плану, добиваясь от учеников не только знания, но и понимания метода, которым они получены. Герберт не был ученым и не внес что-то новое в существовавший в его время компендиум знаний. Однако его точный и ясный ум позволял систематизировать доступные ему сведения и излагать их просто и понятно. Герберт заражал своих учеников духовной энергией, вручая им лампады знания, которые впоследствии ярким светом вспыхивали в разных уголках Европы. Среди его воспитанников были короли и государственные деятели; по крайней мере, тринадцать епископов и архиепископов, шесть настоятелей крупных монастырей, известные схоластики. Самым знаменитым из них был Фульберт (ок. 980–1028) из кафедральной школы при Шартрском соборе, которая явилась предшественницей Сорбонны и стала самым авторитетным центром гуманизма в XII веке.

Диспут в Равенне

В Европе никто не осмеливался оспаривать у Герберта пальму первенства в точных науках, но по части тривия он нашел соперника в лице немецкого схоластика Отриха, которому не давали покоя ученые лавры главы реймской школы. Отрих был монахом монастыря св. Маврикия в Магдебурге и преподавателем монастырской школы, привлекавшей к себе многочисленных учеников. Характер у Отриха, надо полагать, был непростой, мнения о своей учености он был самого высокого, и поэтому, рассорившись, в конце концов, с магдебургским архиепископом, он сделался придворным ученым, продолжая преподавательскую деятельность и по-прежнему собирая вокруг себя множество учеников. Завидуя славе Герберта, Отрих послал одного из них в Реймс с поручением послушать и записать его лекции. Оказалось, что взгляды на классификацию наук у соперников-схоластиков не совпадают, и Отрих принялся везде трубить об ошибках Герберта, говоря, что он будто бы не имеет никакого понятия о различиях между высшим, божественным, и низшим, человеческим, знаниями. Не без злорадства сообщил он об этом и Оттону II, который, однако, не мог допустить и мысли о том, что Герберт ошибается. Случай разрешить спор представился в декабре 980 года, когда Адальберон в сопровождении Герберта совершил путешествие в Италию. Диспут состоялся в присутствии императора в Равенне, куда съехались схоластики со всей Европы. В течение целого дня, перескакивая с темы на тему, диспутанты терзали себя и многочисленных слушателей примерно такими речами:

Герберт: Конечная причина, то есть цель философии заключается в познании божественного и человеческого.

Отрих: Такое определение слишком многословно. Философ должен быть краток, а цель философии можно определить одним словом.

Герберт: Далеко не все причины или цели могут быть определены одним словом. Платон, например, определяет причину сотворения мира тремя словами: «добрая воля Бога».

Отрих: Но слово «добрая» в этом определении излишне, так как Бог не может желать зла.

Герберт: Бог действительно не может быть злокозненным, однако слово «добрая» имеет все-таки здесь логическое значение. По своей субстанции Бог только добр, все же сотворенное им является причастным добру. Поэтому упомянутое слово поставлено здесь именно с целью одновременно определить и саму сущность божественной природы. Кроме того, для доказательства того, что не всякая причина может быть выражена одним словом, скажу, что причину тени нельзя выразить короче формулы: «тело, противопоставленное свету».

И так далее, и тому подобное…

Герберт, захватив инициативу в споре, говорил и говорил, пока Оттон II наклоном головы не дал знак окончить диспут. По общему мнению присутствующих зрителей победа осталась за реймским схоластиком, и Отрих с позором удалился в Магдебург.

Книжник

Но не только блестящая эрудиция caput scholae и новые методы обучения привлекали в Реймс учеников. Не было в Европе книголюба, который бы не мечтал поработать в огромной библиотеке Герберта или одолжить на время что-либо из его книжных сокровищ. А он был неутомим в поисках рукописей, причем – что для него характерно – собирал, в основном, произведения античных классиков и вовсе не интересовался патристикой (впрочем, можно предположить, что он уже имел в достаточном числе сочинения отцов церкви).

Аббату Экберту Герберт писал: «Я усердно собираю библиотеку… Не только в Риме и в других частях Италии, но также в Германии и Лотарингии я нанимал писцов и с помощью щедрых друзей покупал в этих провинциях за большие деньги рукописи. Поэтому мы и вас просим поступить таким же образом. Мы укажем в конце письма перечень авторов, копии трудов которых мы хотели бы получить. Дабы не злоупотреблять вашей добротой, посылаем пергамен для копииста и необходимые денежные средства. Отдыхая или трудясь, мы учим тому, что знаем, и изучаем то, в чем несведущи».