Цифровое моделирование на C#

Если расчет освещенности идет для прожектора, то можно сократить количество вычислений, использовав тот факт, что диффузная составляющая одинакова для всех точек в пределах одного треугольника.

Существует еще один подход к освещению как полигональных, так и других типов моделей. Если мы умеем вычислять значение цвета для произвольной точки объекта, то можно рассчитать освещенность для каждой точки модели. Это, так называемый, метод попиксельного освещения. Понятно, что он является наиболее ресурсоемким из всех. Этот метод может применяться в областях, где скорость расчета освещенности не так важна по сравнению с качеством – например, в мультипликации, где картинки подготавливаются заранее и не так важно, как долго отрисовывался конкретный кадр.

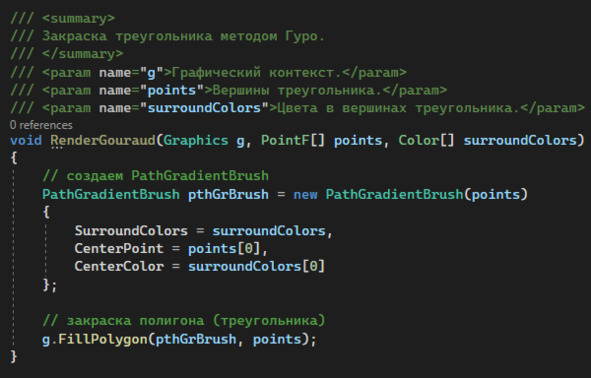
В качестве практической вставки посмотрим, как закрасить треугольник в соответствии с методом Гуро. В графической библиотеке GDI+ присутствует необходимый функционал, чтобы линейно интерполировать цвета между тремя вершинами. (см. листинг ниже)

Моделирование тумана

Вид модели зависит не только от того, какие источники света ее освещают, но и от наличия атмосферных эффектов, в частности, тумана. Благодаря удачной настройке таких эффектов можно изменить эмоциональное восприятие сцены, сделать ее более реалистичной или добавить некий мистический налет.

В этой части урока мы научимся моделировать присутствие тумана на сцене. Мы смоделируем туман, который равномерно скрывает объекты в направлении глубины сцены. Действие такого тумана легко объяснить следующими словами: чем ближе к нам объект, тем более четко мы его видим и тем меньшее значение оказывает туман на цвета объекта, и наоборот, чем дальше объект, тем менее четко мы его видим и тем большее значение оказывает туман (его цвет) на то, каким мы видим объект. Можно сказать, что корректирующее действие тумана является функцией расстояния от наблюдателя до объекта.

Рассмотрим формулу, с помощью которой можно вычислять цвет 3D-модели в условиях тумана:

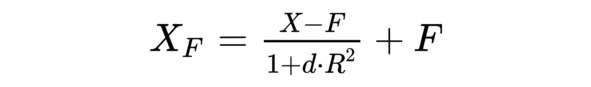
XF – цвет 3D-модели с учетом тумана.

F – цвет тумана (в природе, как правило, это белый цвет, но можно использовать и другие цвета).

R – расстояние от наблюдателя до объекта.

X – исходный цвет объекта, вычисленный например, по методу Фонга.

d – параметр тумана (плотность).

Как работает эта формула? Если R=0, то есть объект находится перед наблюдателем, тогда XF равно исходному цвету объекта. Если же устремить R в бесконечность, XF устремится к цвету тумана. Не стоит рассматривать эту формулу как некоторую каноническую и единственно правильную. Она является искусственно сконструированной и хорошо показала себя на практике (см. дополнительные материалы). В данной формуле выражение R2 может быть заменено на любую другую монотонно-возрастающую функцию, зависящую от R. При этом туман будет как-то по-другому «растворять» объект.

Отображение 3D-модели

Поскольку мы определили трехмерную модель как совокупность полигонов (треугольников), то отображение модели сводится к отображению этой совокупности. Как отобразить эту совокупность чтобы модель выглядела корректно? Существует несколько подходов к решению этой задачи. Мы изложим один из наиболее простых методов. Итак, чтобы наша 3D-модель выглядела правдоподобно, нам нужно проделать следующее: необходимо отсортировать наши треугольники по оси Z в порядке удаленности от наблюдателя. В качестве Z-координаты можно взять минимум по Z для всех трех вершин. То есть отображаться треугольники должны по мере приближения к наблюдателю – от самых дальних к ближним. Этот подход называется алгоритмом художника. Он очень прост, нагляден и легко реализуем. Но он также имеет ряд недостатков. Например, алгоритм не позволяет получить корректную картину в случае взаимно перекрывающихся треугольников. В этом случае следует разбивать конфликтный треугольник на несколько меньших. Второй проблемой является то, что система прорисовывает области, которые впоследствии будут перекрыты, на что тратятся лишние вычислительные ресурсы.

Особый случай представляет из себя ситуация, когда на сцене присутствует только одна 3D-модель и она является выпуклым многогранником (например, кубом), в этом случае сортировка не требуется. Достаточно просто отобразить видимые треугольники. Однако мы пока не выясняли, как определить, видим треугольник наблюдателю или нет. Давайте сформулируем простой критерий видимости треугольника для наблюдателя: треугольник виден наблюдателю в том и только в том случае, если угол между его нормалью и вектором на наблюдателя лежит в пределах от 0 до 90 градусов (является острым). Это условие может быть сформулировано по другому – треугольник виден наблюдателю в случае, если скалярное произведение вектора нормали и вектора, направленного на наблюдателя, больше нуля. Если для определенности предположить, что вектор на наблюдателя имеет следующие координаты (0, 0, -1), то условие видимости треугольника принимает очень простой вид: треугольник виден наблюдателю тогда и только тогда, когда Z-координата его вектора нормали меньше нуля.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.