Цифровое моделирование на C#

Интерполяция

Иногда нам известны лишь значения функции в некоторых точках. При этом аналитическое выражение функции неизвестно, получить его крайне трудно или вообще невозможно. Задача интерполяции ставится как задача восстановления значений функции внутри области определения. Основная идея здесь состоит в том, чтобы имея конечный набор значений, построить по нему аналитическое выражение таким образом, чтобы оно выдавало значения близкие к уже имеющимся.

Делать это можно разными способами. В данной части урока мы рассмотрим два способа интерполяции – многочлен Лагранжа и линейный тренд.

Многочлен Лагранжа

Пусть имеется набор из N-значений функции (Xi, Yi), i=1… N. При этом сама функция нам неизвестна. Обладая этим набором мы хотели бы вычислять значение функции при любом значении X. Будем искать аналитическое выражение для искомой функции в виде многочлена степени N-1.

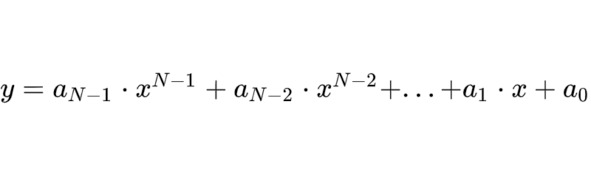
Подставив значение каждой точки (Xi, Yi) в эту формулу, мы получим систему из N-уравнений относительно коэффициентов многочлена. Можно доказать, что если все Xi различны между собой, данная система всегда имеет единственное решение. Всегда существует многочлен, проходящий через каждую заданную точку. Получившуюся формулу можно использовать для вычислений значений в промежуточных точках. Недостатком этого подхода является то, что нужно решать линейную систему и если точек много, это может потребовать значительных вычислительных ресурсов.

Французский математик Жозеф Луи Лагранж (1736—1813 г.г.) предложил следующую формулу для интерполяционного полинома:

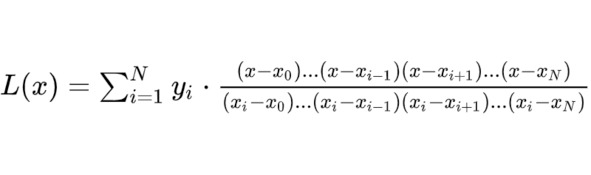
Используя данную формулу, мы можем вычислять значение многочлена, проходящего через заданный набор точек, не зная самих коэффициентов многочлена!

Пример: Пусть даны следующий три точки (1, 1), (4, 2), (8, 5). Тогда, согласно формуле Лагранжа, значения многочлена, проходящего через эти точки, можно вычислять по формуле:

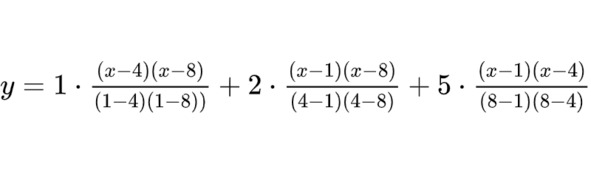
Линейный тренд

В случае интерполяции набора точек многочленом мы получаем аналитическое выражение, с помощью которого можно получать значения в промежуточных точках, причем в самих исходных точках у нас будет полное совпадение. Иногда исходные значения меняются по некоторому линейному закону, но в силу погрешностей измерений и влияния других вероятностных факторов, они не лежат на одной прямой. Можно сказать, что данные линейны, но в них присутствует некоторый «шум». В этом случае нет смысла добиваться точного совпадения значений интерполяционной формулы и исходных данных. Гораздо важнее уловить сам линейный закон. Эту задачу решает линейный тренд. Не стремясь пройти через какую-либо исходную точку, линейный тренд стремится соответствовать самому закону, по которому эти точки получены.

Пусть имеется набор из N-точек (Xi, Yi), i=1..N. Будем искать интерполяционную формулу в виде y=a⋅x+b. При этом потребуем, чтобы сумма квадратов разностей между исходным значением и аппроксимированным была минимальна.

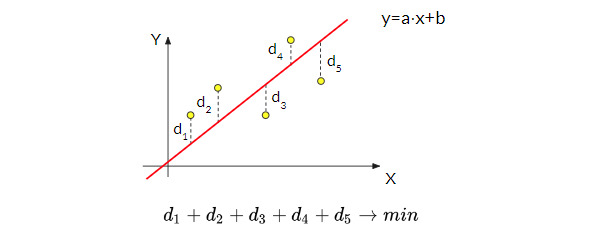
рис. 1.11

Имея набор исходных точек, нам нужно найти неизвестные коэффициенты a и b. Запишем условие о минимальности суммы квадратов между исходными значениями и аппроксимированными в виде:

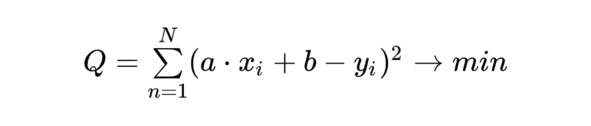
Получение a и b незатруднительно само по себе, но требует некоторых знаний из дифференциального исчисления. Опуская некоторые выкладки, можно показать, что a и b являются решениями следующей системы линейных уравнений:

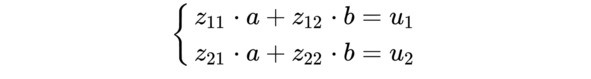
где

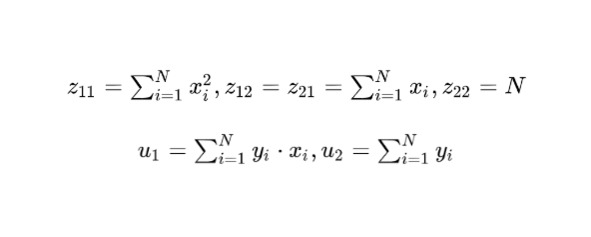
Данный метод построения линейного тренда по заданному набору точек носит название метода наименьших квадратов. Этот метод можно использовать не только для того, чтобы вычислять значение в промежуточных точках (задача интерполяции), но и за пределами минимального и максимального значений по X (задача экстраполяции). Метод наименьших квадратов позволяет предсказывать новое значение y по x, имея исходный набор точек. Этот метод также лежит в основе линейных моделей машинного обучения.

Заключение

На этом наш первый урок завершен. Рекомендуем ознакомиться с дополнительными материалами, которые можно скачать по ссылке https://gitverse.ru/dmitrypavlov74/DMBook. В папке L1 вы найдете два проекта: первый Chart2D посвящен построению графиков, второй Interpolation2D – интерполяционным методам.

Урок 2. 3D моделирование

Цифровые модели в пространстве

Введение

Создание компьютерных игр и CAD-систем невозможно без глубокого понимания того, как устроены трехмерные цифровые модели, как они создаются, трансформируются и освещаются. Все это (создание, трансформирование и освещение трехмерных объектов) мы подробно разберем в этом уроке. Также мы научимся строить поверхности, накладывать текстуры на объекты, рисовать тени и моделировать туман.

3D-моделирование

Цифровое 3D-моделирование – это процесс создания трехмерного представления объекта путем манипулирования ребрами и вершинами в моделируемом трехмерном пространстве. Вы наверняка видели результаты трехмерного моделирования в фильмах, анимациях и видеоиграх, которые наполнены фантастическими существами и структурами.

3D-моделирование используется в самых разных областях, включая инженерию, архитектуру, развлечения, кино, спецэффекты, разработку игр и коммерческую рекламу.

Сама тема 3D-моделирования необычайно интересна и очень востребована в современном мире. В IT-индустрии существует даже профессия 3D-дизайнера (например, 2D-дизайнеров не существует). Справедливости ради нужно отметить, что к разработчику 3D-систем предъявляются повышенные требования в области математики. Наш второй урок направлен как раз на то, чтобы читатель научился понимать основные этапы, связанные с работой в 3D-моделировании. Хочется сразу успокоить читателя: в математическом аппарате, необходимом для работы с 3D-моделями, нет ничего сложного, хотя знаний здесь понадобится больше, чем при построении графиков.

Преобразование точек в трехмерном пространстве

Поскольку трехмерные модели так или иначе задаются набором точек, чтобы изменять положение и размер объекта в пространстве, достаточно уметь изменять положение точки. Мы рассмотрим следующую группу преобразований: поворот, масштабирование и параллельный перенос. Именно к этим трем действиям и сводится трансформация трехмерной модели. Существует унифицированный подход к этим преобразованиям, а именно все эти операции можно свести к умножению матрицы на вектор. Для преобразования точек в трехмерном пространстве используются матрицы порядка 4x4.

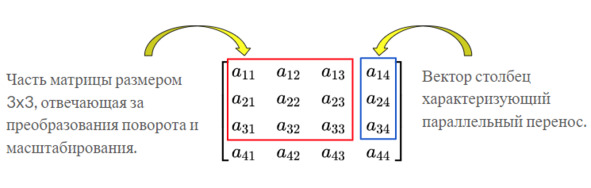
рис. 2.1

Вращение

Далее для каждого преобразования укажем матрицу, которая ему соответствует. Сначала рассмотрим матрицы, которые соответствуют вращению.

Поворот вокруг оси Х:

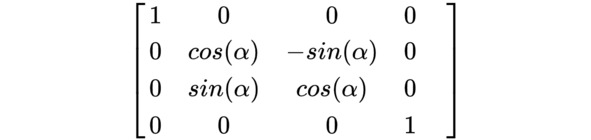
Поворот вокруг оси Y:

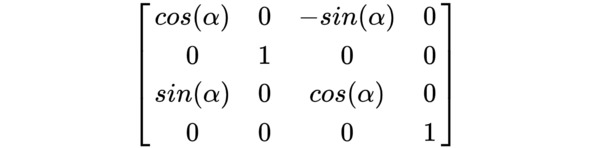
Поворот вокруг оси Z:

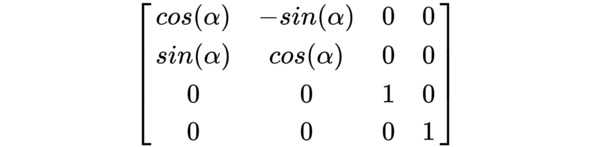
α – угол поворота, заданный в радианах. Поворот осуществляется против часовой стрелки, если смотреть навстречу оси.

Мы рассмотрели матрицы поворота точки вокруг координатных осей. Также на практике может потребоваться повернуть точку вокруг произвольной оси. Пусть ось вращения задана единичным вектором v (x, y, z). Тогда матрица поворота вокруг этого вектора имеет вид:

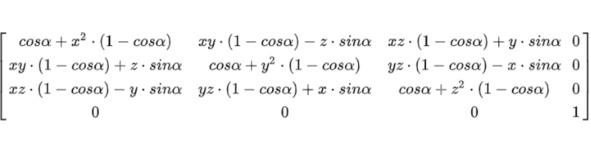
Масштабирование

Матрица масштабирования (изменения размеров объекта с сохранением подобия) имеет вид:

Где с – это коэффициент масштабирования. Если коэффициент с> 1, то точка удаляется от начала координат, если 0 <с <1, то приближается. Если же с <0, то происходит зеркальное отражение точки относительно начала координат. С помощью масштабирования можно управлять размером модели, увеличивая или уменьшая его.

Параллельный перенос

Матрица, соответствующая параллельному переносу точки на вектор с координатами (a, b, c), имеет вид:

Для вращения и масштабирования можно было бы использовать матрицы порядка 3x3, но параллельный перенос уже не может быть описан как матричное преобразование в пространстве этой размерности – для этого требуются матрицы размерности на единицу больше. Использование матриц 4x4, прежде всего, дает нам возможность унифицировать подход к преобразованиям в пространстве – все трансформации модели всегда сводятся к умножению матрицы на вектор. Сами по себе матричные преобразования просты и во многих прикладных библиотеках хорошо оптимизированы. Чтобы иметь возможность умножать матрицу 4x4 на трехмерный вектор, к вектору добавляют формальную четвертую координату w, равную 1: (x, y, z) -> (x, y, z, 1).

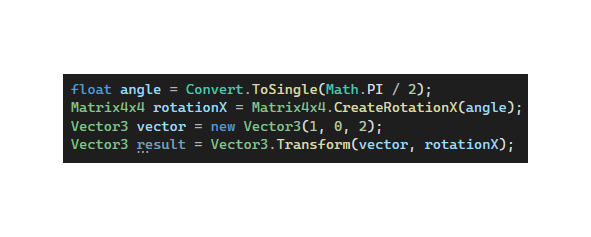
Поскольку наши рассуждения привязаны к конкретному языку программирования, то отметим, что в среде NET уже реализован необходимый функционал для работы с объектами в трехмерном пространстве. В частности, пространство имен System.Numerics содержит матрицы и векторы различных размерностей, а также разнообразные методы для работы с ними. Листинг ниже демонстрирует поворот точки с координатами (1, 0, 2) на угол в 90 градусов. В результате мы получаем точку с координатами (1, -2, 0).

Перспективные преобразования

Перспективные преобразования обеспечивают отображение пространственных моделей на какой-либо поверхности в соответствии с теми, кажущимися сокращениями их размеров, изменениями очертаний и форм, которые наблюдаются в природе. Использование перспективных преобразований делает отображение моделей на экране более реалистичным. Близкие объекты кажутся большими, а далекие маленькими, дорога сужается к горизонту и т. п (рис. 2.2).

рис. 2.2

Смысл перспективных преобразований представлен на рисунках ниже. Пусть нам необходимо отобразить на экране треугольник ABC. Если проекция не используется (рис. 2.3), то берутся обычные ортогональные проекции точек этого треугольника на плоскость проектирования (как правило, это плоскость Z=0),

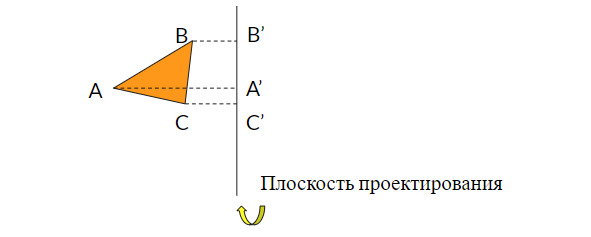
рис. 2.3

При использовании проекции (рис. 2.4), образ точки на плоскость проектирования получается как точка пересечения луча, выходящего из центра проекции, проходящего через исходную точку и плоскости проекции.

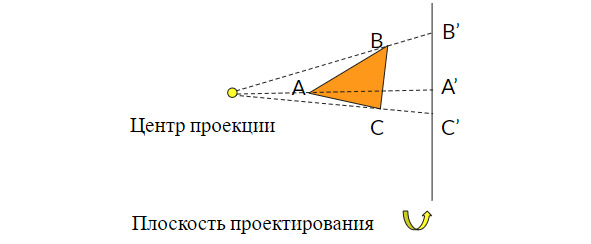
рис. 2.4

Если мы отображаем точку (x, y, z) без использования проективных преобразований, то, по сути, мы просто игнорируем третью координату. При использовании перспективы координата z будет влиять на координаты x и y.

Существует несколько типов проекций. Рассмотрим одноточечную проекцию как пример наиболее простого перспективного преобразования. Нашей задачей будет вычислить новые координаты точки для отображения с учетом перспективы. Для примера рассмотрим плоскость XOZ и вычислим координату X с учетом перспективного преобразования.

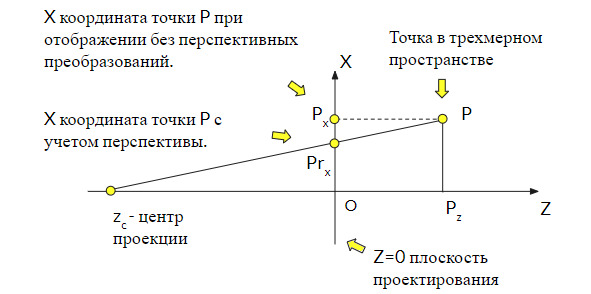
рис. 2.5

Воспользовавшись подобием треугольников (Zc, Prx, 0) и (Zc, P, Pz) и выразив значение для Prx, получаем:

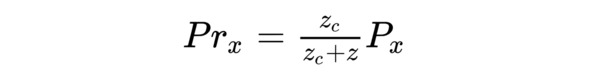
Аналогичные рассуждения можно провести и в плоскости YOZ. Таким образом, если центр проекции находится в точке (0, 0, -Zc), то новые координаты точки с учетом перспективного преобразования можно вычислить по формуле ниже.

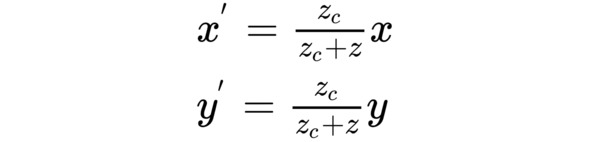
x’, y’ – координаты точки с учетом перспективы; x, y, z – исходные координаты точки.

При одноточечной проекции учитывается только Z-координата. При удалении точки по оси Z от центра проекции его координаты по X и Y будут стремиться к нулю.

Перспективные преобразования, в отличии от, например, вращения и масштабирования, являются мнимыми, они не влияют на форму и положение предметов, а являются лишь кажущимися. Это означает, например, что если к 3D-модели перед отображением были применены перспективные преобразования, то после отображения они должны быть отменены.

Посмотрите, как выглядит цифровая модель куба в приложении Advanced3DModels (см. дополнительные материалы) с применением одноточечной проекции:

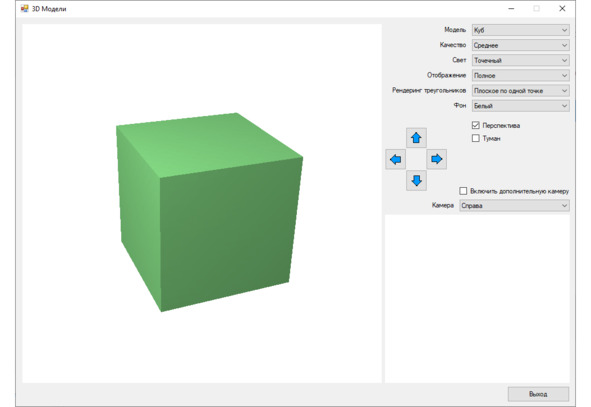
рис. 2.6

Полигональные модели

Полигональное моделирование – это разновидность трехмерного моделирования. Модель при этом задается набором точек. Если три точки заданы в качестве вершин и соединены ребрами, то они формируют треугольник (полигон), который имеет цвет или текстуру. Совокупность таких треугольников позволяет смоделировать практически любой объект. Недостаток полигонального моделирования состоит в том, что сами треугольники должны иметь очень маленький размер, иначе объект будет иметь огранённый вид. Это означает, что если для модели на сцене предполагается увеличение, ее необходимо моделировать с большим количеством полигонов, даже несмотря на то, что большинство из них будут лишними при удалении от объекта. Тем не менее, для простого моделирования такой подход считается вполне приемлемым.

Реалистичное освещение полигональных моделей

В этой части нашего повествования мы разберем способы, позволяющие моделировать освещение трехмерного объекта. Сначала давайте разберем особенности восприятия мира посредством органов зрения. Человек, по сути, видит мир плоским. Сетчатка глаза плоская, а, следовательно, и само изображение, спроецированное на сетчатку, тоже является плоским. Тем не менее, мы воспринимаем мир вокруг себя как объемный, имеющий глубину. Это достигается за счет того, что мозг подвергает плоскую картинку «цифровой» обработке, благодаря которой человек способен видеть объем и форму. На процесс формирования объемного изображения также большое значение оказывает тот факт, что человек имеет два глаза. Из разности изображений, мозг извлекает дополнительную информацию об объеме. Но самую большую информацию о форме объекта человек получает из игры света и тени, а также за счет бликов на его поверхности. Таким образом, реалистичное освещение модели является очень важной частью трехмерного моделирования.

Для полигональных моделей освещение сводится к освещению совокупности треугольников из которых состоит модель. Достаточно уметь освещать один треугольник в зависимости от его положения в пространстве и положения источников света, чтобы суметь осветить всю модель.

Распространение света в реальном мире – это чрезвычайно сложное явление, зависящее от слишком многих факторов, и располагая ограниченными вычислительными ресурсами, мы не можем себе позволить учитывать в расчетах все нюансы. Поэтому методы освещения, которые мы будем описывать, основаны на использовании приближенных к реальности, упрощенных математических моделей, которые дают хороший визуальный эффект, но при этом рассчитываются гораздо проще.

Прежде, чем начать изучение методов освещения, кратко коснемся самих источников света. Все источники света разделим на два типа: прожекторы и точечные источники. Прожектором называется источник света, лучи которого параллельны друг другу. Точечный источник – это источник света, который испускает световые лучи во все стороны.

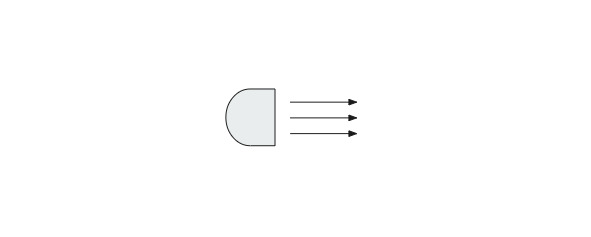
рис. 2.7

Лучи-прожекторы параллельны друг другу (рис. 2.7)

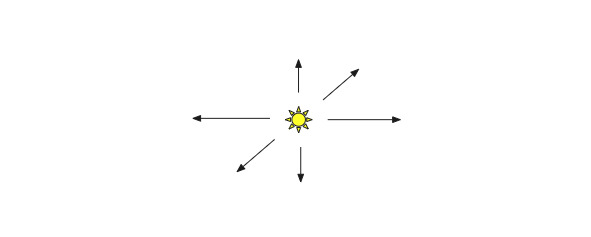
рис. 2.8

Точечный источник излучает свет во все стороны (рис. 2.8)

С точки зрения освещения для нас будет важно, что все лучи от прожектора падают на поверхность под одним и тем же углом. У точечного источника каждый луч падает на поверхность под своим углом.

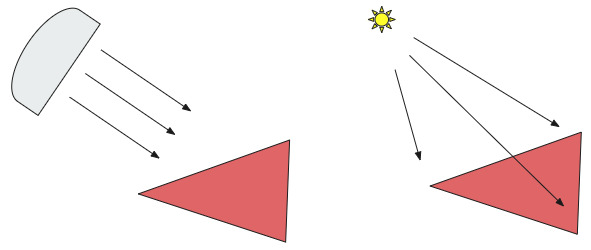
рис. 2.9

Модель Фонга

Одной из наиболее часто используемых моделей освещения является модель освещения Фонга. Она состоит из трех составляющих: фоновой (ambient, англ.), диффузной (diffuse, англ.) и зеркальной (specular, англ.). Цвет в конкретной выбранной точке треугольника зависит от этих трех составляющих освещения. Далее разберем каждую составляющую в отдельности.

Фоновая составляющая

Пусть X – исходный цвет треугольника, а A – константа, лежащая между 0 и 1, которая характеризует фоновое освещение. Тогда фоновая составляющая F равна:

F = A ⋅ X

Тот факт, что константа A лежит между 0 и 1, означает, что исходное значение цвета X будет уменьшено. Вообще, значение параметра А для всех объектов, не излучающих свет самостоятельно, как то всевозможные лампочки или флуоресцентные материалы, равно 0. Значение фоновой составляющей не зависит от наличия источников света и характеризует самостоятельное свечение объекта.

Диффузная составляющая

Диффузное освещение имитирует воздействие на объект направленного источника света. Это наиболее визуально значимый компонент модели освещения. Чем меньше угол между нормалью (нормалью называется ненулевой вектор перпендикулярный плоскости треугольника) к треугольнику и вектором, направленным на источник света, тем большую яркость ему придает диффузная составляющая.

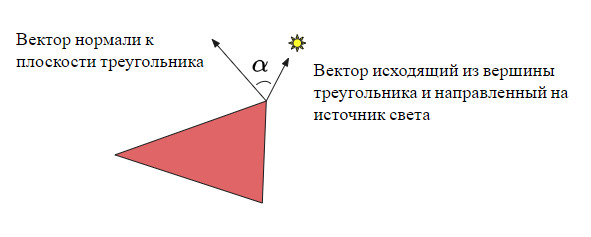
рис. 2.10

Расчет диффузной составляющей происходит согласно формуле ниже:

D = d ⋅ X ⋅ (1 + cos (α)) / 2

D – диффузная составляющая.

d – значимость источника света. Этот параметр можно интерпретировать как яркость этого источника относительно других. Сумма значений d для всех источников должна быть равна 1.

X – исходный цвет поверхности треугольника.

α – угол между вектором нормали к поверхности и вектором, исходящим из вершины треугольника и направленным на источник света.

Легко заметить, то значение диффузной составляющей максимально, когда вектор нормали сонаправлен с вектором, направленным на источник света, и минимально, когда данные вектора антиколлинеарны. Как следует из формулы, диффузная составляющая всегда больше или равна нулю. Если поверхность освещается прожектором, то диффузная составляющая будет одна и та же для каждой точки треугольника. В случае точечного источника диффузная составляющая будет различна для каждой точки.

Зеркальная составляющая

Зеркальная составляющая имитирует яркое пятно света (блик), которое появляется на блестящих объектах. Расчет зеркальных бликов, как и в случае диффузного освещения, основан на векторе направления источника света и нормали к поверхности объекта, но помимо этого в вычислениях учитывается позиция наблюдателя, то есть направление, в котором наблюдатель смотрит на фрагмент.

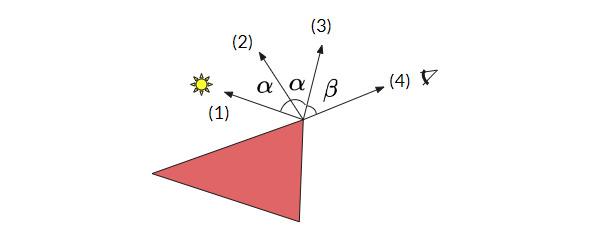
рис. 2.11

(1) – вектор, исходящий из вершины треугольника и направленный на источник света.

(2) – вектор нормали к плоскости треугольника.

(3) – отраженный от поверхности луч света.

(4) – вектор, исходящий из вершины треугольника и направленный на наблюдателя.

α – угол между вектором нормали и вектором, направленным на источник света.

β – угол между отраженным от поверхности треугольника лучом света и вектором, направленным на наблюдателя.

Зеркальную составляющую освещения можно вычислить по следующей формуле:

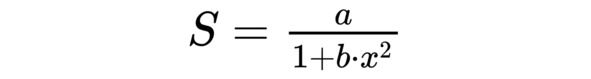
S – зеркальная составляющая.

a – параметр, характеризующий яркость светового блика.

b – параметр, характеризующий размер светового блика на поверхности. Чем больше b, тем меньше блик.

x = 1-cos (β)

β – угол между отраженным лучом света и вектором, направленным на наблюдателя. Этот угол должен варьироваться в пределах от 0 до 90 градусов. Если угол больше, чем 90 градусов, это означает, что поверхность не освещается лучами от источника света или наблюдатель не может видеть данную поверхность. В этом случае зеркальная составляющая равна 0.

Если мы построим график функции, с помощью которой вычисляется зеркальная составляющая, то мы получим примерно такой график (рис. 2.12) (в зависимости от параметров a и b вид графика может немного меняться).

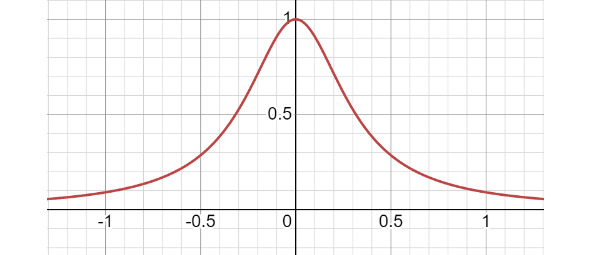
рис. 2.12

Эта функция достигает своего максимума при x=0, то есть когда отраженный луч и вектор, направленный на наблюдателя, сонаправлены. Значение самих параметров a и b полностью зависит от свойств материала поверхности. Например, для металла значение a будет больше, чем для дерева.

Как и диффузная, зеркальная составляющая всегда больше или равна нулю. Но в отличии от диффузной, которая зависит только от угла между нормалью к поверхности и падающим лучом света, значение зеркальной составляющей не является некоторым абсолютным значением, а зависит от позиции наблюдателя.

Формула Фонга

Общее значение освещенности является суммой трех составляющих освещения:

Освещенность = Фоновая + ∑ Диффузная + ∑ Зеркальная

Суммирование идет по всем источникам света, присутствующим на сцене.

Способы освещения

Мы выяснили, как вычислять цвет в произвольной точке треугольника. Но нам необходимо закрасить весь треугольник. Чтобы это сделать, существует несколько вариантов. Первый вариант самый простой (и, соответственно, самый быстрый) – нужно вычислить цвет в произвольной точке (например, в вершине) и закрасить этим цветом весь треугольник. Второй чуть сложнее – это вычислить цвет в трех вершинах треугольника, усреднить эти значения и закрасить этим усредненным значением весь треугольник. И, наконец, третий способ – вычислить цвет в трех вершинах, а для закраски внутренних точек треугольника использовать линейную интерполяцию между вершинами треугольника (метод Гуро). Этот метод позволяет устранить дискретность изменения интенсивности, также он является наиболее ресурсоемким из трех перечисленных, но именно он дает самую качественную картину из описанных выше методов.