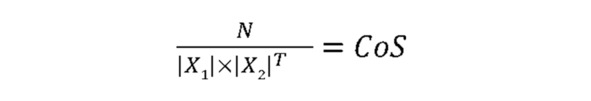Полная версия
PANN: Новая Технология Искусственного Интеллекта. Учебное пособие

PANN: Новая Технология Искусственного Интеллекта
Учебное пособие
Борис Злотин
Владимир Маценко
Редактор Анатолий Гин
© Борис Злотин, 2025
© Владимир Маценко, 2025
ISBN 978-5-0062-7522-5
Создано в интеллектуальной издательской системе Ridero
Ключевые слова
• уникальные свойства
• прозрачность функционирования
• простая математическая модель
• низкая стоимость внедрения и пользования
От авторов
Авторы: Борис Злотин, разработавший теоретические основы теории PANN и программных продуктов на ее основе, и Владимир Маценко, реализовавший группу этих продуктов и участвовавший в создании и тестировании теории, – выражают благодарность тем, кто помогал в этой работе и внес серьезный творческий вклад:
• Дмитрию Песчанскому, нашедшему общую идею нового подхода к конструкциям нейронных сетей.
• ТРИЗ-специалистам Владимиру Просянику, Анатолию Гину, Сергею Фаеру, Олегу Гафурову и Алле Зусман, активно поддерживавших разработку PANN своим опытом, знаниями и талантами.
• Ивану Ивановичу Негрешному – за конструктивную критику, помогавшую увидеть и исправить недостатки.
Часть 1.
Новый вид нейронных сетей: Progress Artificial Neural Network (PANN)
1. Введение в проблему
Откуда взялись нейронные сети и чем они нас не устраивают?
Начало развитию искусственных нейронных сетей положили работы Тьюринга, Мак-Каллока, Питтса и Хебба. На основе их идей Фрэнк Розенблатт в 1958 г. создал первую искусственную нейронную сеть «Персептрон», способную после соответствующего обучения распознавать и на основе распознавания классифицировать разные объекты. К сожалению, в самой концепции персептрона была заложена критическая ошибка, основанная на господствовавшей тогда биологической доктрине Дэйла: «…нейрон использует один и только один нейромедиатор для всех синапсов». Эта доктрина была перенесена во все искусственные нейросети в виде правила: «…один искусственный синапс использует один и только один синаптический вес». Это правило можно назвать доктриной Розенблатта.
В 70-х гг. XX века доктрина Дэйла была отвергнута биологией. А доктрина Розенблатта, к сожалению, до сегодняшнего дня остается неизменной для всех нейронных сетей («рекуррентных», «резонансных», «глубоких», «сверточных», «LSTM», «генеративных», сетей прямого и обратного распространения ошибки и т. п.). Именно она заставляет применять при тренинге сетей итерационный подход, известный как метод градиентного спуска (gradient descent method), требующий огромного объема вычислений. И именно эта доктрина «виновата» в невозможности построить адекватную рабочую теорию нейронных сетей. А также в том, что эти сети характеризуются непрозрачностью и непонятностью, сравнительно низкой скоростью обучения, сложностью доучивания и множеством других «врожденных» проблем. Подробнее о проблемах классических нейронных сетей см. Приложение 1.
Поэтому развитие таких сетей идет в основном методом проб и ошибок. А это ведет к сложности и малой надежности, необходимости использования очень дорогого оборудования, проведения энергоемких вычислений и дорогостоящей ручной работы для обучения.
Критическая «ошибка Розенблатта» была обнаружена исследователями (специалистами по ТРИЗ) deep tech компании Progress Inc. Они же нашли решение, позволяющее исключить эту ошибку. Это позволило создать принципиально новый вид нейронных сетей, названный PANN (Progress Artificial Neural Network). PANN и их работа прозрачны, предсказуемы, требуют в тысячи раз меньших затрат и обеспечивают лучшее решение многих интеллектуальных задач. Идеи PANN защищены 18 патентами во многих странах мира. На основании этих идей уже создано и протестировано несколько вариантов новых софтверов.
2. Научно-технические основы сети PANN
В данной главе мы расскажем об основных конструктивных и научных особенностях сети PANN.
PANN отличается от классических нейронных сетей иной конструкцией главного элемента: так называемого формального нейрона. Новый формальный нейрон позволяет использовать другой способ обучения. В результате:
1. Работа сети стала совершенно прозрачной. Стало возможным построить простую и ясную теорию, предсказывающую результаты действий с нею.
2. PANN может быть реализована на недорогом оборудовании. Расходы на ее обучение и функционирование во много раз меньше, чем у классических нейронных сетей.
3. PANN обучается во много раз быстрее классических нейронных сетей.
4. PANN может в любое время доучиваться.
5. У PANN отсутствует вредный эффект «переобучения».
2.1. НОВАЯ КОНСТРУКЦИЯ ФОРМАЛЬНОГО НЕЙРОНА
Классические нейронные сети построены из типовых «кирпичей» – формальных нейронов простой конструкции, описанных Мак-Каллоком и Питтсом и реализованных Розенблаттом. И главная проблема нейронных сетей – неудачная конструкция этого формального нейрона.
Формальный нейрон Розенблатта имеет один синаптический вес. Главным отличием PANN является формальный нейрон Progress с двумя или более синаптическими весами на каждом синапсе.
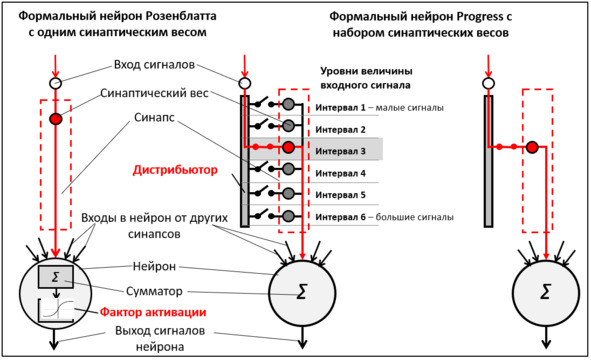
Рис. 1. Сравнение формальных нейронов
На нейроне Progress, как и на нейроне Розенблатта, входные сигналы проходят к сумматору через единственный синаптический вес. Но на нейроне Progress выбор этого веса осуществляется дистрибьютором по величине входного сигнала.
Главные характеристики, описывающие нейрон Progress
• Нейрон Progress оперирует с имиджами, в качестве которых рассматриваются любые числовые (цифровые) последовательности. Такими имиджами могут быть картинки, фильмы, тексты, записи звуков, таблицы, графики и т. п.
• Каждый нейрон Progress связан со всеми входами в сеть. Число входов равно числу цифр в рассматриваемой цифровой последовательности (имидже). Для имиджей в растровой графике это число пикселей. Например, при разрешении 16 × 16 число входов I = 256, при разрешении 32 × 32 число входов I = 1024.
• Число синаптических весов нейрона Progress не менее двух. При работе с черно-белой графикой и простыми таблицами возможно использовать только 2 веса («0» и «1»). При работе с цветными картинками можно использовать любые графические представления, например палитры из 2, 4, 8, 16, 256 и т. д. цветов (весов). Следует отметить, что для эффективного распознавания разных типов имиджей существуют свои оптимальные палитры, которые несложно определить простым тестированием. При этом проявляется неожиданное свойство PANN – оптимальное для распознавания число цветов обычно мало, в экспериментах это число получалось обычно в районе от 6 до 10.
• Число входов – это число членов рассматриваемой цифровой последовательности. Для имиджей в растровой графике это – число пикселей, которое должно быть одинаковым для всех рассматриваемых имиджей. Например, при разрешении 16 × 16 число входов I = 256, при разрешении 32 × 32 число входов I = 1024. При работе с картинками можно использовать любые соотношения сторон прямоугольных картинок. Следует отметить, что, аналогично, для эффективного распознавания разных типов имиджей существуют свои оптимальные разрешения, которые несложно определить простым тестированием. При этом проявляется неожиданное свойство PANN – оптимальное для распознавания число пикселей обычно невелико, например для распознавания разного рода портретов часто наилучшим оказывается разрешение всего 32 × 32.
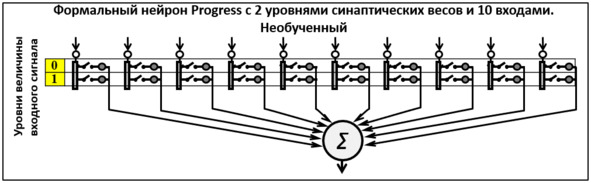
Рис. 2. Однонейронная двухуровневая сеть PANN
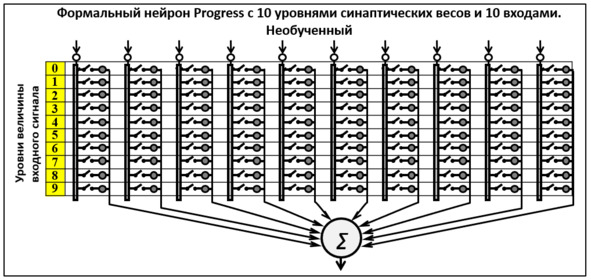
Рис. 3. Однонейронная многоуровневая сеть PANN
2.2. ОБУЧЕНИЕ НЕЙРОНА PROGRESS
Обучение сети PANN существенно проще, чем обучение любых классических сетей.
Трудности обучения классических нейронных сетей связаны с тем, что при обучении нескольким разным имиджам одни из них влияют на синаптические веса других и вносят искажения в обучение друг в друга. Поэтому приходится подбирать веса так, чтобы их набор соответствовал всем имиджам одновременно. Для этого используют метод градиентного спуска, требующий огромного количества итерационных вычислений.
Для обучения сети PANN был разработан принципиально иной подход: «Один нейрон – один имидж», при котором каждый нейрон обучается своему имиджу. При этом не возникает взаимных влияний разных нейронов, обучение становится быстрым и точным.
Обучение нейрона Progress некоторому образу сводится к тому, что дистрибьютор определяет уровень сигнала (в простейшем случае его амплитуду или величину по шкале RGB) и замыкает выключатель, соответствующий интервалу весов, в который попадает данная величина.
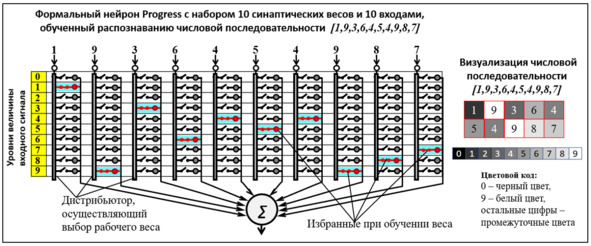
Рис. 4. Обученная однонейронная многоуровневая сеть PANN
Приведенная схема обучения нейрона Progress порождает ряд замечательных свойств сети PANN:
1. Обучение не требует вычислительных операций и поэтому происходит очень быстро.
2. Набор синаптических весов одного нейрона никак не зависит от других нейронов, и поэтому нейроны сети можно обучать как по отдельности, так и группами, а потом обученные нейроны или их группы объединять в сеть.
3. Сеть может доучиваться, то есть можно изменять, добавлять и убирать нужные нейроны в любое время, не влияя при этом на незатронутые данными изменениями нейроны.
4. Обученный нейрон-имидж может быть легко визуализирован с использованием простейших цветовых кодов, связывающих уровни включенных весов с яркостью или цветом пикселей.
2.3. ЗАБАВНЫЙ ПАРАДОКС PANN
На первый взгляд сеть PANN выглядит конструктивно сложнее, чем классические Искусственные Нейронные Сети. Но в действительности PANN проще.
Сеть PANN проще, потому что:
1. В нейроне Розенблатта есть фактор активации, то есть обработка полученного результата посредством нелинейной логистической (сигмовидной) функции, S-кривой и т. п. Без этого нельзя обойтись, но это усложняет нейрон Розенблатта и делает его нелинейным, что приводит к огромным проблемам при обучении. В отличие от него нейрон Progress строго линеен и никаких проблем не порождает.
2. В нейроне Progress имеется дополнительный элемент – дистрибьютор, представляющий собой несложное логическое устройство: демультиплексор. Оно переключает сигнал с одного входа на один из нескольких выходов. В нейроне Розенблатта веса – многобитовые ячейки памяти, допускающие хранение чисел в широком диапазоне, а в PANN могут использоваться простейшие ячейки (триггеры), способные хранить только числа – 1 и 0.
3. PANN, в отличие от классических сетей, не требует очень большой памяти и вычислительной мощности компьютера, поэтому можно использовать дешевые компьютеры и требуется намного меньшее количество электроэнергии.
4. PANN позволяет решать сложные задачи на однослойной сети.
5. PANN требует в десятки и даже сотни раз меньшего количества имиджей в обучающей выборке.
Таким образом открываются возможности создавать на основе PANN полноценные продукты, используя не очень дорогую и экономичную в плане потребления энергии компьютерную технику.

Рис. 5. Долгое и дорогое обучение против быстрого и дешевого
2.4. МАТЕМАТИЧЕСКАЯ ОСНОВА РАСПОЗНАВАНИЯ
НА НЕЙРОНЕ PROGRESS
Линейность нейрона Progress приводит к тому, что и сеть, построенная на этих нейронах, линейна. А это обеспечивает ее полную прозрачность, простоту описывающей ее теории и применяемой математики.
В 1965 г. Лотфи Заде ввел понятие «нечетких множеств» и идею «нечеткой логики». В какой-то степени это послужило подсказкой для нашей работы по разработке математического обоснования и логики PANN. Математические операции в PANN направлены на сравнение неточно совпадающих имиджей и оценку степени их расхождения в виде коэффициентов сходства.
2.4.1. Определения
В 2009 г. было сделано интересное открытие, названное «нейрон Мерлин Монро» или в других источниках «нейрон бабушки». Оказывается, в голове человека знания по определенным темам «разнесены» по отдельным нейронам и нейронным группам, которые связаны друг с другом ассоциативными связями, так что возбуждение может передаваться с одних нейронов на другие. Это знание вместе с принятой парадигмой «Один нейрон – один имидж» позволило построить систему распознавания PANN.
Введем понятие «нейрон-имидж» – это нейрон, обученный конкретному имиджу. В PANN каждый нейрон-имидж – это реализованная функциональная зависимость (функция) Y = f (X), где:
X – некоторый числовой массив (вектор), обладающий свойствами:
при X = A, f (A) = N
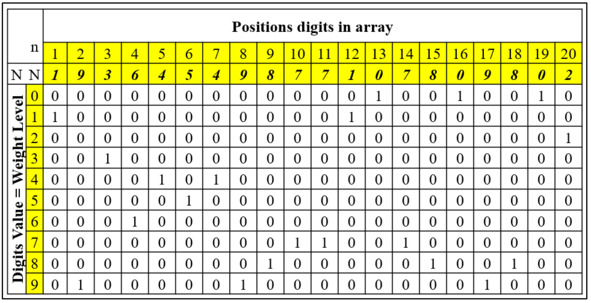
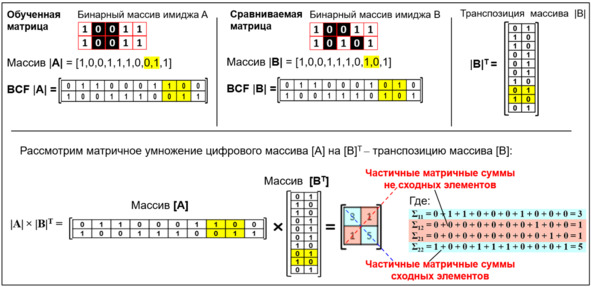
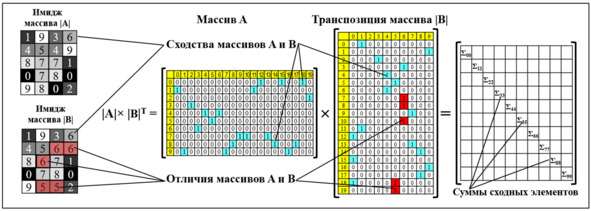
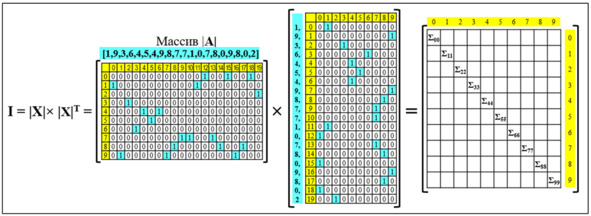
при X ≠ A, f (A) A – некоторая заданная величина. N – размерность вектора X, то есть число цифр в этом векторе. Для записи числовых векторов X предложен специальный формат, запатентованный компанией Progress Inc. Этот формат, названый Binary Comparison Format (BCF), представляет собой прямоугольную бинарную цифровую матрицу, в которой: • количество колонок равно длине N (числу цифр) массива; • количество строк равно числу выбранных для сети уровней веса k; • каждая значащая цифра обозначается единицей (1) в соответствующей строке, а отсутствие цифры – нулем (0); • каждая строка соответствует некоторой значащей цифре записываемого числового массива, то есть в строке, обозначенной как «нулевая», цифра «1» соответствует цифре «0» в исходном массиве, а в строке, обозначенной как «девятая», – цифра «1» соответствует цифре 9 в массиве; • в каждой колонке матрицы имеется одна единица, соответствующая величине данной цифры, а все остальные величины в этой колонке равны 0; • сумма всех единиц в матрице массива равна длине N данного массива, например для массива из 20 цифр она равна 20; • суммарное количество нулей и единиц в матрице каждого массива равно произведению длины N данного массива на величину основания используемой системы счисления. Пример: BCF-запись массива из 20 десятичных цифр [1, 9, 3, 6, 4, 5, 4, 9, 8, 7, 7, 1, 0, 7, 8, 0, 9, 8, 0,2]. Рис. 6. BCF-имидж как разреженная бинарная матрица Особенностью сетей PANN является то, что обучение нейронов по имиджам, типичное для нейронных сетей, может быть заменено переформатированием файлов, несущих числовые зависимости, к формату BCF, или просто загрузкой в сеть файлов в этом формате. Массивы типа X в формате BCF обозначаются как матрицы |X|. 2.4.2. Сравнение числовых массивов Сравнение объектов, или определение сходства и различия. Определение сходства тех или иных объектов путем их сравнения играет огромную роль в мышлении, позволяет выявлять аналогии и отличия разных объектов – существ, предметов, процессов, идей и т. п. В разных отраслях науки, в первую очередь в Теории Подобия, используются безразмерные коэффициенты сходства или критерии подобия (Coefficient Similarity, или CoS), иногда называемые «мера сходства», «мера ассоциации», «мера подобия» и т. п. Функции сравнения в PANN реализуются через математические операции над матрицами числовых массивов. Рассмотрим простейший алгоритм сравнения через векторное произведение числовых массивов нейронов-имиджей. Даны два массива для сравнения в виде матриц |X1| и |X2|. |X1| × |X2|T – произведение матрицы |X1| на транспонированную матрицу |X2|. Причем величина этого произведения пропорциональна числу совпадающих по месту в BCF-матрице единиц в |X1| и |X2|. |X1| × |X2|T = N, только если |X1| = |X2|; |X1| × |X2|T |X1| × |X2|T = 0, если ни один пиксель этих матриц не совпадает. Рассмотрим отношение: Здесь CoS – Коэффициент Сходства между числовыми векторами X1 и X2 определяет степень близости этих векторов и описываемых этими векторами имиджей. Примеры: Рис. 7. Перемножение матриц для сравнения числовых массивов Рис. 8. Сравнение десятичных числовых массивов |A| и |B| Классические нейронные сети при распознавании только определяют, на какой класс более всего похож некоторый распознаваемый объект. При этом они не могут указать, насколько он похож. Из-за этого распознавание иногда неустойчиво – существуют известные примеры, когда изменения одного пикселя в имидже оказалось достаточным, чтобы его распознавание изменилось. Это значит, что распознавание в классических сетях сильно зависит от случайных шумов. В PANN ситуация иная – величина коэффициента сходства очень четко показывает, насколько существенна разница между имиджами. Разница сходства в одну сотую при формате 32 × 32 пикселя соответствует примерно изменению 10 пикселей. И этого уже достаточно для того, чтобы уверенно отличать имиджи друг от друга. А разница в одну десятую говорит уже о вполне серьезном различии и высокой устойчивости распознавания, малой зависимости распознавания от шумов. В отличие от классических нейронных сетей, сети PANN позволяют резко повысить качество распознавания за счет: • статистической обработки распознавания по классам и по имиджам; • совмещения распознавания по классам и распознавания непосредственно по имиджам. Причем совмещенное распознавание по классам и по имиджам позволяет решить одну из самых неприятных проблем, ограничивающих применение нейронных сетей в медицине и ряде других приложений – проблему прозрачности и объяснимости результатов работы сети. Подробнее мы расскажем об этом в разделе «4.6. Распознавание сетью PANN». 2.4.3. Оценка достоверности и точности распознавания Достоверность и точность распознавания имиджей нейронными сетями крайне важны для их использования. Точность и надежность распознавания классической нейронной сети определяется путем тестирование нескольких десятков, сотен или тысяч имиджей и подсчета числа правильных и неправильных распознаваний. Это очень спорный тест. Из-за непрозрачности работы классических сетей распознавание сильно зависит от случайных особенностей обучения: • иногда результаты обучения плохо воспроизводятся, одна и та же сеть, обученная на одних и тех же имиджах, в одних случаях будет распознавать лучше, в других хуже; • нет способов адекватной оценки точности и надежности распознавания по каждому из имиджей; • влияние отбора тестовых имиджей. Иногда их подбирают специально для обеспечения нужного результата. Распознавание сетью PANN оценивается по числовому коэффициенту сходства рассматриваемого имиджа: 1. С любым набором загруженных в сеть отдельных имиджей. 2. Со всеми классами, которым обучена данная сеть. При этом и классы, и отдельные имиджи ранжируются по степени сходства, что позволяет точно оценить величину различий между всеми сравниваемыми классами и тем самым оценить точность и надежность распознавания. Безусловно, возможно формально (с точки зрения машины) правильное, но не устраивающее нас распознавание. Даже люди нередко распознают других людей не по главным, а по второстепенным признакам. Например, оценивая сходство не по чертам лица, а по одежде. Бывает, что при распознавании человеческих лиц особенности освещения оказываются более весомыми, чем черты лица. Но проблемы такого рода вполне решаемы в PANN несколькими путями, в частности: 1. Выравнивание освещенности известными графическими или математическими средствами. 2. Введение системы оценки весомости признаков и фильтрации некоторых признаков. 3. Создание набора пересекающихся классов, как будет показано в ниже. 4. Создание «комитета по распознаванию» – логической экспертной системы, выносящей «приговор» по сумме распознаваний по разным классам и имиджам. То есть фактически воспроизводящей то, что делает человек, внимательно приглядывающийся к объекту. 2.4.4. Индексация числовых последовательностей в BCF Индексация для быстрого поиска информации. Сегодня в компьютерной науке широко применяется поисковая индексация. Файлы индексов облегчают поиск информации, и по своему объему они в 10 раз меньше, чем исходные файлы. Но для разных типов файлов (например, графических) индексация сложнее, и поиск не всегда работает адекватно. PANN обеспечивает более организованный и стандартизированный подход к индексации и поиску. Использование разработанного компанией Progress Inc формата Binary Comparison Format (BCF) позволяет строить стандартные и универсальные поисковые индексы – идентификаторы для любой числовой последовательности как линейные свертки цифрового массива. Эти индексы представляют собой последовательность матричных сумм с совпадающими номерами строк и столбцов, полученных путем векторного умножения данного цифрового массива на его собственную транспозицию. И они могут быть по объему гораздо меньше, чем при обычной индексации. При этом процесс поиска по индексам происходит параллельно, что обеспечивает его многократное ускорение. Например, имеется имидж, описанный в виде матрицы |X| с числом пикселей n =1024 и числом уровней веса k = 10. Определим произведение матрицы |X| на ее собственную транспозицию |X|T как индекс I. I = |X| × |X|T = |Σ| = Σ00, Σ11, Σ22, Σ33, Σ44, … Σ99: Рис. 9. Формирование поисковых индексов Длина полученного индекса равна числу уровней веса и не зависит от числа пикселей в имиджах. Значит, если установить стандартное число весов 10 (это удобно, так как соответствует принятой десятичной системе счисления), то эти индексы будут стандартными для всех библиотек, что обеспечит возможность их всеобщего применения. Каждый образ в библиотеках распознавания должен быть снабжен индексом. Распознавание каждого нового образа должно начинаться с формирования его индекса, на его базе происходит быстрое распознавание по подготовленным библиотекам. Точность распознавания по такого рода индексам может быть очень высокой. Например, при использовании десятизначной системы счисления (10 уровней веса от 0 до 9), даже если мы ограничимся только первой значащей цифрой каждой суммы, индексом будет комбинация из 10 однозначных, то есть вероятность случайных совпадений индексов не превысит 10—10 (1 / 10 миллиардов). 2.4.5. Паттерны подобия и другие способы сравнения и индексации в BCF Выявление паттернов для понимания происходящих событий и управления ими – одно из важнейших приложений нейронных сетей. Существует немало причин, почему два разных имиджа могут быть подобными или казаться нам подобными. Чаще всего подобие определяется общностью происхождения и/или изготовления разных объектов. Либо тем, что разные объекты изменяются и развиваются по некоторым общим паттернам, например по законам природы. Паттерны в живописи или музыке могут быть законами композиции, конструирования машин – формулами сопромата, в обществе – обычаями и государственными законами и так далее.