Logic: Deductive and Inductive

If C is D, E is F;

If A is B, C is D:

∴ If A is B, E is F.

If we recognise particular hypothetical propositions (see chap. v. § 4), it is obvious that such Syllogisms may be constructed in all the Moods and Figures of the Categorical Syllogism; and of course they may be translated into Categoricals. We often reason in this hypothetical way. For example:

If the margin of cultivation be extended, rents will rise;

If prices of produce rise, the margin of cultivation will be extended:

∴ If prices of produce rise, rents will rise.

But the function of the Hypothetical Syllogism (commonly so called), as also of the Disjunctive Syllogism (to be discussed in the next section) is to get rid of the conditional element of the premises, to pass from suspense to certainty, and obtain a decisive categorical conclusion; whereas these Syllogisms with two hypothetical premises leave us still with a hypothetical conclusion. This circumstance seems to ally them more closely with Categorical Syllogisms than with those that are discussed in the present chapter. That they are Categoricals in disguise may be seen by considering that the above syllogism is not materially significant, unless in each proposition the word 'If' is equivalent to 'Whenever.' Accordingly, the name 'Hypothetical Syllogism,' is here employed in the older usage.

§ 2. A Disjunctive Syllogism consists of a Disjunctive Major Premise, a Categorical Minor Premise, and a Categorical Conclusion.

How many Moods are to be recognised in this kind of argument depends on whether the alternatives of the Disjunctive Premise are regarded as mutually exclusive or possibly coincident. In saying 'Either A is B, or C is D,' do we mean 'either, but not both,' or 'either, it may be both'? (See chap. v. § 4.)

When the alternatives of the Disjunctive are not exclusive, we have only the

Either wages fall, or the weaker hands are dismissed;

Wages do not fall:

∴ The weaker hands are dismissed.

But we cannot argue—

Wages fall:

∴ The weaker hands are not dismissed;

since in 'hard times' both events may happen together.

Rule of the Modus tollendo ponens: If one alternative be denied, the other is affirmed.

When, however, the alternatives of the Disjunctive are mutually exclusive, we have also the

Either the Tories or the Whigs win the election;

The Tories win:

∴ The Whigs do not win.

We may also, of course, argue as above in the Modus tollendo ponens—

The Tories do not win:

∴ The Whigs do.

But in this example, to make the Modus tollendo ponens materially valid, it must be impossible that the election should result in a tie. The danger of the Disjunctive Proposition is that the alternatives may not, between them, exhaust the possible cases. Only contradictory alternatives are sure to cover the whole ground.

Rule of the Modus ponendo tollens: If one alternative be affirmed, the other is denied.

Since a disjunctive proposition may be turned into a hypothetical proposition (chap. v. § 4,) a Disjunctive Syllogism may be turned into a Hypothetical Syllogism:

Similarly the Modus ponendo tollens is equivalent to that kind of Modus ponens which may be formed with a negative major premise; for if the alternatives of a disjunctive proposition be exclusive, the corresponding hypothetical be affirmative or negative:

Hence, finally, a Disjunctive Syllogism being equivalent to a Hypothetical, and a Hypothetical to a Categorical; a Disjunctive Syllogism is equivalent and reducible to a Categorical. It is a form of Mediate Inference in the same sense as the Hypothetical Syllogism is; that is to say, the conclusion depends upon an affirmation, or denial, of the fulfilment of a condition implied in the disjunctive major premise.

§ 3. The Dilemma is perhaps the most popularly interesting of all forms of proof. It is a favourite weapon of orators and wits; and "impaled upon the horns of a dilemma" is a painful situation in which every one delights to see his adversary. It seems to have been described by Rhetoricians before finding its way into works on Logic; and Logicians, to judge from their diverse ways of defining it, have found some difficulty in making up their minds as to its exact character.

There is a famous Dilemma employed by Demosthenes, from which the general nature of the argument may be gathered:

If Æschines joined in the public rejoicings, he is inconsistent; if he did not, he is unpatriotic;

But either he joined, or he did not join:

Therefore he is either inconsistent or unpatriotic.

That is, reduced to symbols:

If A is B, C is D; and if E is F, G is H:

But either A is B, or E is F;

∴ Either C is D or G is H (Complex Constructive).

This is a compound Conditional Syllogism, which may be analysed as follows:

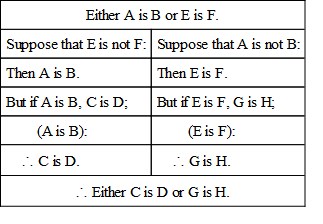
A Dilemma, then, is a compound Conditional Syllogism, having for its Major Premise two Hypothetical Propositions, and for its Minor Premise a Disjunctive Proposition, whose alternative terms either affirm the Antecedents or deny the Consequents of the two Hypothetical Propositions forming the Major Premise.

The hypothetical propositions in the major premise, may have all four terms distinct (as in the above example); and then the conclusion is a disjunctive proposition, and the Dilemma is said to be Complex. Or the two hypothetical propositions may have a common antecedent or a common consequent; and then the conclusion is a categorical proposition, and the Dilemma is said to be Simple.

Again, the alternatives of the disjunctive minor premise may be affirmative or negative: if affirmative, the Dilemma is called Constructive; and if negative, Destructive.

Using, then, only affirmative hypothetical propositions in the major premise, there are four Moods:

1. The Simple Constructive—

If A is B, C is D; and if E is F, C is D:

But either A is B, or E is F:

∴ C is D.

If the Tories win the election, the Government will avoid innovation; and if the Whigs win, the House of Lords will prevent them innovating:

But either the Tories or the Whigs will win:

∴ There will be no innovation.

2. The Complex Constructive—

If A is B, C is D; and if E is F, G is H:

But either A is B, or E is F:

∴ Either C is D or G is H.

If appearance is all that exists, reality is a delusion; and if there is a substance beyond consciousness, knowledge of reality is impossible:

But either appearance is all, or there is a substance beyond consciousness:

∴ Either reality is a delusion, or a knowledge of it is impossible.

3. Simple Destructive—

If A is B, C is D; and if A is B, E is F:

But either C is not D, or E is not F:

∴ A is not B.

If table-rappers are to be trusted, the departed are spirits; and they also exert mechanical energy:

But either the departed are not spirits, or they do not exert mechanical energy:

∴ Table-rappers are not to be trusted.

4. Complex Destructive—

If A is B, C is D; and if E is F, G is H:

But either C is not D, or G is not H:

∴ Either A is not B, or E is not F.

If poetic justice is observed, virtue is rewarded; and if the mirror is held up to Nature, the villain triumphs:

But either virtue is not rewarded, or the villain does not triumph:

∴ Either poetic justice is not observed, or the mirror is not held up to Nature.

Such are the four Moods of the Dilemma that emerge if we only use affirmative hypotheticals for the major premise; but, certainly, it is often quite as natural to employ two negative hypotheticals (indeed, one might be affirmative and the other negative; but waive that); and then four more moods emerge, all having negative conclusions. It is needless to intimidate the reader by drawing up these four moods in battle array: they always admit of reduction to the foregoing moods by obverting the hypotheticals. Still, by the same process we may greatly decrease the number of moods of the Categorical Syllogism; and just as some Syllogisms are most simply expressed in Celarent or Cesare, so some Dilemmas are most simply stated with negative major premises—e.g., The example of a Simple Constructive Dilemma above given would run more naturally thus: If the Tories win, the Government will not innovate; and if the Whigs, the Lords will not let them: and similarly Demosthenes' Dilemma—If Æschines joined, he is not consistent; and if he did not, he is not patriotic. Moreover, the propriety of recognising Dilemmas with negative major premises, follows from the above analysis of the Dilemma into a combination of Conditional Syllogisms, even if (as in § 1 of this chapter) we take account of only four Moods of the Hypothetical Syllogism.

In the rhetorical use of the Dilemma, it may be observed that the disjunction in the minor premise ought to be obvious, or (at any rate) easily acceptable to the audience. Thus, Either the Tories or the Whigs will win; Either Æschines joined in the rejoicings, or he did not; such propositions are not likely to be disputed. But if the orator must stop to prove his minor premise, the smacking effect of this figure (if the expression be allowed) will be lost. Hence the minor premises of other examples given above are only fit for a select audience. That Either ghosts are not spirits, or they do not exert mechanical energy, supposes a knowledge of the principle, generally taught by physical philosophers, that only matter is the vehicle of energy; and that Either appearance is all, or there is substance beyond consciousness, is a doctrine which only metaphysical philosophers could be expected to understand, and upon which they could not be expected to agree. However, the chief danger is that a plausible disjunction may not be really such as to exclude any middle ground: Either the Tories or the Whigs win, is bad, if a tie be possible; though in the above argument this is negligible, seeing that a tie cannot directly cause innovations. Either Æschines joined in the rejoicings, or he did not, does not allow for a decent conformity with the public movement where resistance would be vain; yet such conformity as need not be inconsistent with subsequent condemnation of the proceedings, nor incompatible with patriotic reserve founded on a belief that the rejoicings are premature and ominous.

Another rhetorical consideration is, that the alternatives of the disjunctive conclusion of a Complex Dilemma should both point the same way, should be equally distasteful or paradoxical. 'Either inconsistent or unpatriotic': horrid words to a politician! 'Either no reality or no possible knowledge of it': very disappointing to an anxious inquirer! Thus the disjunctive conclusion is as bad for an opponent as the categorical one in a Simple Dilemma.

Logicians further speak of the Trilemma, with three Hypotheticals and a corresponding triple Disjunction; and of a Polylemma, with any further number of perplexities. But anyone who has a taste for logical forms may have it amply gratified in numerous text-books.

CHAPTER XIII

TRANSITION TO INDUCTION

§ 1. Having now discussed Terms, Propositions, Immediate and Mediate Inferences, and investigated the conditions of formal truth or consistency, we have next to consider the conditions of material truth: whether (or how far) it is possible to arrive at propositions that accurately represent the course of nature or of human life. Hitherto we have dealt with no sort of proof that gives any such assurance. A valid syllogism guarantees the truth of its conclusion, provided the premises be true: but what of the premises? The relation between the premises of a valid syllogism and its conclusion is the same as the relation between the antecedent and consequent of a hypothetical proposition. If A is B, C is D: grant that A is B, and it follows that C is D; and, similarly, grant the premises of a syllogism, and the conclusion follows. Again, grant that C is not D, and it follows that A is not B; and, similarly, if the conclusion of a valid syllogism be false, it follows that one, or other, or both of the premises must be false. But, once more, grant that C is D, and it does not follow that A is B; so neither, if the conclusion of a syllogism be true, does it follow that the premises are. For example:—

Sociology is an exact science;

Mathematics is a branch of Sociology:

∴ Mathematics is an exact science.

Here the conclusion is true although the premises are absurd. Or again:—

Mathematics is an exact science;

Sociology is a branch of Mathematics:

∴ Sociology is an exact science.

Here the major premise is true, but the minor is false, and the conclusion is false. In both cases, however, whether the conclusion be true or false, it equally follows from the premises, if there is any cogency in Barbara. The explanation of this is, that Barbara has only formal cogency; and that whether the conclusion of that, or any other valid mood, shall be true according to fact and experience, depends upon how the form is filled up. How to establish the premises, then, is a most important problem; and it still remains to be solved.

§ 2. We may begin by recalling the distinction between the denotation and connotation of a general term: the denotation comprising the things or events which the term is a name for; the connotation comprising the common qualities on account of which these things are called by the same name. Obviously, there are very few general terms whose denotation is exhaustively known; since the denotation of a general term comprises all the things that have its connotation, or that ever have had, or that ever will have it, whether they exist here, or in Australia, or in the Moon, or in the utmost stars. No one has examined all men, all mammoths, all crystals, all falling bodies, all cases of fever, all revolutions, all stars—nor even all planets, since from time to time new ones are discerned. We have names for animals that existed long before there were men to observe them, and of which we know only a few bones, the remains of multitudinous species; and for others that may continue to exist when men have disappeared from the earth.

If, indeed, we definitely limit the time, or place, or quantity of matter to be explored, we may sometimes learn, within the given limits, all that there is to know: as all the bones of a particular animal, or the list of English monarchs hitherto, or the names of all the members of the House of Commons at the present time. Such cases, however, do not invalidate the above logical truth that few general terms are exhaustively known in their denotation; for the very fact of assigning limits of time and place impairs the generality of a term. The bones of a certain animal may be all examined, but not the bones of all animals, nor even of one species. The English monarchs that have reigned hitherto may be known, but there may be many still to reign.

The general terms, then, with which Logic is chiefly concerned, the names of Causes and Kinds, such as gravitation, diseases, social events, minerals, plants and animals, stand for some facts that are, or have been, known, and for a great many other similar ones that have not been, and never will be, known. The use of a general term depends not upon our direct knowledge of everything comprised in its denotation, but upon our readiness to apply it to anything that has its connotation, whether we have seen the thing or not, and even though we never can perceive it; as when a man talks freely of the ichthyosaurus, or of the central heat of planets, or of atoms and ether.

Hence Universal Propositions, which consist of general terms, deceive us, if we suppose that their predicates are directly known to be related to all the facts denoted by their subjects. In exceptional cases, in which the denotation of a subject is intentionally limited, such exhaustive direct knowledge may be possible; as that "all the bones of a certain animal consist of phosphate of lime," or that every member of the present Parliament wears a silk hat. But what predication is possible concerning the hats of all members of Parliament from the beginning? Ordinarily, then, whilst the relation of predicate to subject has been observed in some cases, in much the greater number of cases our belief about it depends upon something besides observation, or may be said (in a certain sense) to be taken on trust.

'All rabbits are herbivorous': why do we believe that? We may have seen a few wild rabbits feeding: or have kept tame ones, and tried experiments with their diet; or have read of their habits in a book of Natural History; or have studied the anatomy and physiology of the digestive system in many sorts of animals: but with whatever care we add testimony and scientific method to our own observation, it still remains true that the rabbits observed by ourselves and others are few in comparison with those that live, have lived and will live. Similarly of any other universal proposition; that it 'goes beyond the evidence' of direct observation plainly follows from the fact that the general terms, of which such propositions consist, are never exhaustively known in their denotation. What right have we then to state Universal Propositions? That is the problem of Inductive Logic.

§ 3. Universal Propositions, of course, cannot always be proved by syllogisms; because to prove a universal proposition by a syllogism, its premises must be universal propositions; and, then, these must be proved by others. This process may sometimes go a little way, thus: All men are mortal, because All animals are; and All animals are mortal, because All composite bodies are subject to dissolution. Were there no limit to such sorites, proof would always involve a regressus ad infinitum, for which life is too short; but, in fact, prosyllogisms soon fail us.

Clearly, the form of the Syllogism must itself be misleading if the universal proposition is so: if we think that premises prove the conclusion because they themselves have been established by detailed observation, we are mistaken. The consideration of any example will show this. Suppose any one to argue:

All ruminants are herbivorous;

Camels are ruminants:

∴ Camels are herbivorous.

Have we, then, examined all ruminants? If so, we must have examined all camels, and cannot need a syllogism to prove their herbivorous nature: instead of the major premise proving the conclusion, the proof of the conclusion must then be part of the proof of the major premise. But if we have not examined all ruminants, having omitted most giraffes, most deer, most oxen, etc., how do we know that the unexamined (say, some camels) are not exceptional? Camels are vicious enough to be carnivorous; and indeed it is said that Bactrian camels will eat flesh rather than starve, though of course their habit is herbivorous.

Or, again, it is sometimes urged that—

All empires decay:

∴ Britain will decay.

This is manifestly a prediction: at present Britain flourishes, and shows no signs of decay. Yet a knowledge of its decay seems necessary, to justify any one in asserting the given premise. If it is a question whether Britain will decay, to attempt (while several empires still flourish) to settle the matter by asserting that all empires decay, seems to be 'a begging of the question.' But although this latter case is a manifest prediction, it does not really differ from the former one; for the proof that camels are herbivorous has no limits in time. If valid, it shows not only that they are, but also that they will be, herbivorous.

Hence, to resort to a dilemma, it may be urged: If all the facts of the major premise of any syllogism have been examined, the syllogism is needless; and if some of them have not been examined, it is a petitio principii. But either all have been examined, or some have not. Therefore; the syllogism is either useless or fallacious.

§ 4. A way of escape from this dilemma is provided by distinguishing between the formal and material aspects of the syllogism considered as a means of proof. It begs the question formally, but not materially; that is to say, if it be a question whether camels are herbivorous, and to decide it we are told that 'all ruminants are,' laying stress upon the 'all,' as if all had been examined, though in fact camels have not been, then the question as to camels is begged. The form of a universal proposition is then offered as evidence, when in fact the evidence has not been universally ascertained. But if in urging that 'all ruminants are herbivorous' no more is meant than that so many other ruminants of different species are known to be herbivorous, and that the ruminant stomach is so well adapted to a coarse vegetable diet, that the same habit may be expected in other ruminants, such as camels, the argument then rests upon material evidence without unfairly implying the case in question. Now the nature of the material evidence is plainly this, that the resemblance of camels to deer, oxen, etc., in chewing the cud, justifies us in believing that they have a further resemblance in feeding on herbs; in other words, we assume that resemblance is a ground of inference.

Another way of putting this difficulty which we have just been discussing, with regard to syllogistic evidence, is to urge that by the Laws of Syllogism a conclusion must never go beyond the premises, and that therefore no progress in knowledge can ever be established, except by direct observation. Now, taking the syllogism formally, this is true: if the conclusion go beyond the premises, there must be either four terms, or illicit process of the major or minor term. But, taking it materially, the conclusion may cover facts which were not in view when the major premise was laid down; facts of which we predicate something not as the result of direct observation, but because they resemble in a certain way those facts which had been shown to carry the predicate when the major premise was formed.

'What sort of resemblance is a sufficient ground of inference?' is, therefore, the important question alike in material Deduction and in Induction; and in endeavouring to answer it we shall find that the surest ground of inference is resemblance of causation. For example, it is due to causation that ruminants are herbivorous. Their instincts make them crop the herb, and their stomachs enable them easily to digest it; and in these characters camels are like the other ruminants.

§ 5. In ch. ix, § 3, the Dictum de omni et nullo was stated: 'Whatever may be predicated of a term distributed may be predicated of anything that can be identified with that term.' Nothing was there said (as nothing was needed) of the relations that might be implied in the predication. But now that it comes to the ultimate validity of predication, we must be clear as to what these relations are; and it will also be convenient to speak no longer of terms, as in Formal Logic, but of the things denoted. What relations, then, can be determined between concrete facts or phenomena (physical or mental) with the greatest certainty of general truth; and what axioms are there that sanction mediate inferences concerning those relations?

In his Logic (B. II. c. 2, § 3) Mill gives as the axiom of syllogistic reasoning, instead of the Dictum: "A thing which co-exists with another thing, which other co-exists with a third thing, also co-exists with that third thing." Thus the peculiar properties of Socrates co-exist with the attributes of man, which co-exist with mortality: therefore, Socrates is mortal. But, again, he says that the ground of the syllogism is Induction; that man is mortal is an induction. And, further, the ground of Induction is causation; the law of causation is the ultimate major premise of every sound induction. Now causation is the principle of the succession of phenomena: how, then, can the syllogism rest on an axiom concerning co-existence? On reflection, too, it must appear that 'Man is mortal' predicates causation: the human constitution issues in death.