Logic: Deductive and Inductive

As for Fig. IV., no particular advantage has been claimed for it. It is of comparatively late recognition (sometimes called the 'Galenian,' after Galen, its supposed discoverer); and its scientific claim to exist at all is disputed. It is said to be a mere inversion of Fig. I.; which is not true in any sense in which Figs. II. and III. may not be condemned as partial inversions of Fig. I., and as having therefore still less claim to recognition. It is also said to invert the order of thought; as if thought had only one order, or as if the order of thought had anything to do with Formal Logic. Surely, if distinction of Figure be recognised at all, the Fourth Figure is scientifically necessary, because it is inevitably generated by an analysis of the possible positions of the middle term.

§ 10. Is Reduction necessary, however; or have not all the Figures equal and independent validity? In one sense not only every Figure but each Mood has independent validity: for any one capable of abstract thinking sees its validity by direct inspection; and this is true not only of the abstract Moods, but very frequently of particular concrete arguments. But science aims at unifying knowledge; and after reducing all possible arguments that form categorical syllogisms to the nineteen Moods, it is another step in the same direction to reduce these Moods to one form. This is the very nature of science: and, accordingly, the efforts of some Logicians to expound separate principles of each Figure seem to be supererogatory. Grant that they succeed; and what can the next step be, but either to reduce these principles to the Dictum, or the Dictum and the rest to one of these principles? Unless this can be done there is no science of Formal Logic. If it is done, what is gained by reducing the principles of the other Figures to the Dictum, instead of the Moods of the other Figures to those of the first Figure? It may, perhaps, be said that to show (1) that the Moods of the second, third, and fourth Figures flow from their own principles (though, in fact, these principles are laboriously adapted to the Moods); and (2) that these principles may be derived from the Dictum, is the more uncompromisingly gradual and regular method: but is not Formal Logic already sufficiently encumbered with formalities?

§ 11. Euler's diagrams are used to illustrate the syllogism, though not very satisfactorily, thus:

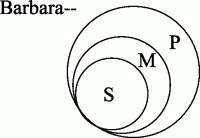
Fig. 5.

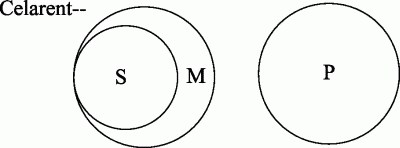
Fig. 6.

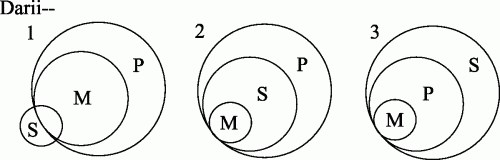
Fig. 7.

Remembering that 'Some' means 'It may be all,' it is plain that any one of these diagrams in Fig. 7, or the one given above for Barbara, may represent the denotative relations of P, M and S in Darii; though no doubt the diagram we generally think of as representing Darii is No. 1 in Fig. 7.

Remembering that A may be U, and that, therefore, wherever A occurs there may be only one circle for S and P, these syllogisms may be represented by only two circles, and Barbara by only one.

Fig. 8.

Here, again, probably, we generally think of No. 1 as the diagram representing Ferio; but 2, or 3, or that given above for Celarent, is compatible with the premises.

If instead of dealing with M, P, and S, a concrete example be taken of Darii or Ferio, a knowledge of the facts of the case will show what diagram is suitable to it. But, then, surely it must be possible to do without the diagram. These diagrams, of course, can be used to illustrate Moods of the other Figures.

CHAPTER XI

ABBREVIATED AND COMPOUND ARGUMENTS

§ 1. In ordinary discussion, whether oral or written, it is but rarely that the forms of Logic are closely adhered to. We often leave wide gaps in the structure of our arguments, trusting the intelligence of those addressed to bridge them over; or we invert the regular order of propositions, beginning with the conclusion, and mentioning the premises, perhaps, a good while after, confident that the sagacity of our audience will make all smooth. Sometimes a full style, like Macaulay's, may, by means of amplification and illustration, spread the elements of a single syllogism over several pages—a pennyworth of logic steeped in so much eloquence. These practices give a great advantage to sophists; who would find it very inconvenient to state explicitly in Mood and Figure the pretentious antilogies which they foist upon the public; and, indeed, such licences of composition often prevent honest men from detecting errors into which they themselves have unwittingly fallen, and which, with the best intentions, they strive to communicate to others: but we put up with these drawbacks to avoid the inelegance and the tedium of a long discourse in accurate syllogisms.

Many departures from the strictly logical statement of reasonings consist in the use of vague or figurative language, or in the substitution for one another of expressions supposed to be equivalent, though, in fact, dangerously discrepant. Against such occasions of error the logician can provide no safeguard, except the advice to be careful and discriminating in what you say or hear. But as to any derangement of the elements of an argument, or the omission of them, Logic effectually aids the task of restoration; for it has shown what the elements are that enter into the explicit statement of most ratiocinations, namely, the four forms of propositions and what that connected order of propositions is which most easily and surely exposes the validity or invalidity of reasoning, namely, the premises and conclusion of the Syllogism. Logic has even gone so far as to name certain abbreviated forms of proof, which may be regarded as general types of those that actually occur in debate, in leading articles, pamphlets and other persuasive or polemic writings—namely, the Enthymeme, Epicheirema and Sorites.

§ 2. The Enthymeme, according to Aristotle, is the Syllogism of probable reasoning about practical affairs and matters of opinion, in contrast with the Syllogism of theoretical demonstration upon necessary grounds. But, as now commonly treated, it is an argument with one of its elements omitted; a Categorical Syllogism, having one or other of its premises, or else its conclusion, suppressed. If the major premise be suppressed, it is called an Enthymeme of the First Order; if the minor premise be wanting, it is said to be of the Second Order; if the conclusion be left to be understood, there is an Enthymeme of the Third Order.

Let the following be a complete Syllogism:

All free nations are enterprising;

The Dutch are a free nation:

∴ The Dutch are enterprising.

Reduced to Enthymemes, this argument may be put thus:

In the First Order:

The Dutch are a free nation:

∴ The Dutch are enterprising.

In the Second Order—

All free nations are enterprising;

∴ The Dutch are enterprising.

In the Third Order—

All free nations are enterprising;

And the Dutch are a free nation.

It is certainly very common to meet with arguments whose statement may be represented by one or other of these three forms; indeed, the Enthymeme is the natural substitute for a full syllogism in oratory: whence the transition from Aristotle's to the modern meaning of the term. The most unschooled of men readily apprehend its force; and a student of Logic can easily supply the proposition that may be wanted in any case to complete a syllogism, and thereby test the argument's formal validity. In any Enthymeme of the Third Order, especially, to supply the conclusion cannot present any difficulty at all; and hence it is a favourite vehicle of innuendo, as in Hamilton's example:

Every liar is a coward;

And Caius is a liar.

The frankness of this statement and its reticence, together, make it a biting sarcasm upon Caius.

The process of finding the missing premise in an Enthymeme of either the First or the Second Order, so as to constitute a syllogism, is sometimes called Reduction; and for this a simple rule may be given: Take that term of the given premise which does not occur in the conclusion (and which must therefore be the Middle), and combine it with that term of the conclusion which does not occur in the given premise; the proposition thus formed is the premise which was requisite to complete the Syllogism. If the premise thus constituted contain the predicate of the conclusion, the Enthymeme was of the First Order; if it contain the subject of the conclusion, the Enthymeme was of the Second Order.

That a statement in the form of a Hypothetical Proposition may really be an Enthymeme (as observed in chap. v. § 4) can easily be shown by recasting one of the above Enthymemes thus: If all free nations are enterprising, the Dutch are enterprising. Such statements should be treated according to their true nature.

To reduce the argument of any ordinary discourse to logical form, the first care should be to make it clear to oneself what exactly the conclusion is, and to state it adequately but as succinctly as possible. Then look for the evidence. This may be of an inductive character, consisting of instances, examples, analogies; and, if so, of course its cogency must be evaluated by the principles of Induction, which we shall presently investigate. But if the evidence be deductive, it will probably consist of an Enthymeme, or of several Enthymemes one depending on another. Each Enthymeme may be isolated and expanded into a syllogism. And we may then inquire: (1) whether the syllogisms are formally correct according to Barbara (or whatever the appropriate Mood); (2) whether the premises, or the ultimate premises, are true in fact.

§ 3. A Monosyllogism is a syllogism considered as standing alone or without relation to other arguments. But, of course, a disputant may be asking to prove the premises of any syllogism; in which case other syllogisms may be advanced for that purpose. When the conclusion of one syllogism is used to prove another, we have a chain-argument which, stated at full length, is a Polysyllogism. In any Polysyllogism, again, a syllogism whose conclusion is used as the premise of another, is called in relation to that other a Prosyllogism; whilst a syllogism one of whose premises is the conclusion of another syllogism, is in relation to that other an Episyllogism. Two modes of abbreviating a Polysyllogism, are usually discussed, the Epicheirema and the Sorites.

§ 4. An Epicheirema is a syllogism for one or both of whose premises a reason is added; as—

All men are mortal, for they are animals;

Socrates is a man, for rational bipeds are men:

∴ Socrates is mortal.

The Epicheirema is called Single or Double, says Hamilton, according as an "adscititious proposition" attaches to one or both of the premises. The above example is of the double kind. The Single Epicheirema is said to be of the First Order, if the adscititious proposition attach to the major premise; if to the minor, of the Second Order. (Hamilton's Logic: Lecture xix.)

An Epicheirema, then, is an abbreviated chain of reasoning, or Polysyllogism, comprising an Episyllogism with one or two enthymematic Prosyllogisms. The major premise in the above case, All men are mortal, for they are animals, is an Enthymeme of the First Order, suppressing its own major premise, and may be restored thus:

All animals are mortal;

All men are animals:

∴ All men are mortal.

The minor premise, Socrates is a man, for rational bipeds are men, is an Enthymeme of the Second Order, suppressing its own minor premise, and may be restored thus:

All rational bipeds are men;

Socrates is a rational biped:

∴ Socrates is a man.

§ 5. The Sorites is a Polysyllogism in which the Conclusions, and even some of the Premises, are suppressed until the arguments end. If the chain of arguments were freed of its enthymematic character, the suppressed conclusions would appear as premises of Episyllogisms.

Two varieties of Sorites are recognised, the Aristotelian (so called, though not treated of by Aristotle), and the Goclenian (named after its discoverer, Goclenius of Marburg, who flourished about 1600 A.D.). In order to compare these two forms of argument, it will be convenient to place side by side Hamilton's classical examples of them.

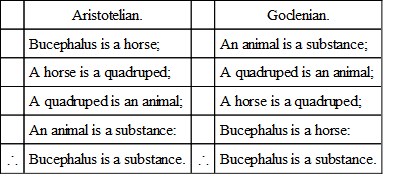
The reader wonders what is the difference between these two forms. In the Aristotelian Sorites the minor term occurs in the first premise, and the major term in the last; whilst in the Goclenian the major term occurs in the first premise, and the minor in the last. But since the character of premises is fixed by their terms, not by the order in which they are written, there cannot be a better example of a distinction without a difference. At a first glance, indeed, there may seem to be a more important point involved; the premises of the Aristotelian Sorites seem to proceed in the order of Fig. IV. But if that were really so the conclusion would be, Some Substance is Bucephalus. That, on the contrary, every one writes the conclusion, Bucephalus is a substance, proves that the logical order of the premises is in Fig. I. Logically, therefore, there is absolutely no difference between these two forms, and pure reason requires either that the "Aristotelian Sorites" disappear from the text-books, or that it be regarded as in Fig. IV., and its conclusion converted. It is the shining merit of Goclenius to have restored the premises of the Sorites to the usual order of Fig. I.: whereby he has raised to himself a monument more durable than brass, and secured indeed the very cheapest immortality.

The common Sorites, then, being in Fig. I., its rules follow from those of Fig. I:

(1) Only one premise can be particular; and, if any, only that in which the minor term occurs.

For, just as in Fig I., a particular premise anywhere else involves undistributed Middle.

(2) Only one premise can be negative; and, if any, only that in which the major term occurs.

For if there were two negative premises, at the point where the second entered the chain of argument there must be a syllogism with two negative premises, which is contrary to Rule 5; whilst if one premise be negative it must be that which contains the major term, for the same reason as in Fig. I., namely, that the conclusion will be negative, and that therefore only a negative major premise can prevent illicit process of the major term.

If we expand a Sorites into its constituent syllogisms, the conclusions successively suppressed will reappear as major premises; thus:

This suffices to show that the Protosyllogism of a Goclenian Sorites is an Enthymeme of the Third Order; after which the argument is a chain of Enthymemes of the First Order, or of the First and Third combined, since the conclusions as well as the major premises are omitted, except in the last one.

Lest it should be thought that the Sorites is only good for arguments so frivolous as the above, I subjoin an example collected from various parts of Mill's Political Economy:—

The cost of labour depends on the efficiency of labour;

The rate of profits depends on the cost of labour;

The investment of capital depends on the rate of profits;

Wages depend on the investment of capital:

∴ Wages depend on the efficiency of labour.

Had it occurred to Mill to construct this Sorites, he would have modified his doctrine of the wages-fund, and would have spared many critics the malignant joy of refuting him.

§ 6. The Antinomy is a combination of arguments by which contradictory attributes are proved to be predicable of the same subject. In symbols, thus:

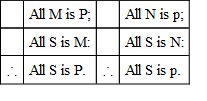
Now, by the principle of Contradiction, S cannot be P and p (not-P): therefore, if both of the above syllogisms are sound, S, as the subject of contradictory attributes, is logically an impossible thing. The contradictory conclusions are called, respectively, Thesis and Antithesis.

To come to particulars, we may argue: (1) that a constitution which is at once a monarchy, an aristocracy and a democracy, must comprise the best elements of all three forms; and must, therefore, be the best of all forms of government: the British Constitution is, therefore, the best of all. But (2) such a constitution must also comprise the worst elements of monarchy, aristocracy and democracy; and, therefore, must be the worst of all forms. Are we, then, driven to conclude that the British Constitution, thus proved to be both the best and worst, does not really exist at all, being logically impossible? The proofs seem equally cogent; but perhaps neither the best nor the worst elements of the simpler constitutions need be present in our own in sufficient force to make it either good or bad.

Again:

Does it, then, follow that 'Man,' as the subject of contradictory attributes, is a nonentity? This doctrine, or something like it, has been seriously entertained; but if to any reader it seem extravagant (as it certainly does to me), he will no doubt find an error in the above arguments. Perhaps the major term is ambiguous.

For other examples it is enough to refer to the Critique of Pure Reason, where Kant sets out the Antinomies of Rational Cosmology. But even if we do not agree with Kant that the human understanding, in attempting to deal with certain subjects beyond its reach, inevitably falls into such contradictory reasonings; yet it can hardly be doubted that we not unfrequently hold opinions which, if logically developed, result in Antinomies. And, accordingly, the Antinomy, if it cannot be imputed to Reason herself, may be a very fair, and a very wholesome argumentum ad hominem. It was the favourite weapon of the Pyrrhonists against the dogmatic philosophies that flourished after the death of Aristotle.

CHAPTER XII

CONDITIONAL SYLLOGISMS

§ 1. Conditional Syllogisms may be generally described as those that contain conditional propositions. They are usually divided into two classes, Hypothetical and Disjunctive.

A Hypothetical Syllogism is one that consists of a Hypothetical Major Premise, a Categorical Minor Premise, and a Categorical Conclusion. Two Moods are usually recognised the Modus ponens, in which the antecedent of the hypothetical major premise is affirmed; and the Modus tollens, in which its consequent is denied.

(1) Modus ponens, or Constructive.

If A is B, C is D;

A is B:

∴ C is D.

If Aristotle's reasoning is conclusive, Plato's theory of Ideas is erroneous;

Aristotle's reasoning is conclusive:

∴ Plato's theory of Ideas is erroneous.

Rule of the Modus ponens: The antecedent of the major premise being affirmed in the minor premise, the consequent is also affirmed in the conclusion.

(2) Modus tollens, or Destructive.

If A is B, C is D;

C is not D:

∴ A is not B.

If Pythagoras is to be trusted, Justice is a number;

Justice is not a number:

∴ Pythagoras is not to be trusted.

Rule of the Modus tollens: The consequent of the major premise being denied in the minor premise, the antecedent is denied in the conclusion.

By using negative major premises two other forms are obtainable: then, either by affirming the antecedent or by denying the consequent, we draw a negative conclusion.

Further, since the antecedent of the major premise, taken by itself, may be negative, it seems possible to obtain four more forms, two in each Mood, from the following major premises:

(1) If A is not B, C is D;

(2) If A is not B, C is not D.

But since the quality of a Hypothetical Proposition is determined by the quality of its consequent, not at all by the quality of its antecedent, we cannot get from these two major premises any really new Moods, that is to say, Moods exhibiting any formal difference from the four previously expounded.

It is obvious that, given the hypothetical major premise—

If A is B, C is D—

we cannot, by denying the antecedent, infer a denial of the consequent. That A is B, is a mark of C being D; but we are not told that it is the sole and indispensable condition of it. If men read good books, they acquire knowledge; but they may acquire knowledge by other means, as by observation. For the same reason, we cannot by affirming the consequent infer the affirmation of the antecedent: Caius may have acquired knowledge; but we cannot thence conclude that he has read good books.

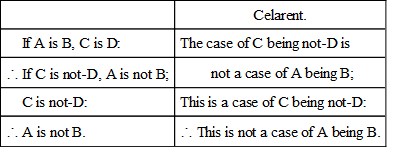
To see this in another light, let us recall chap. v. § 4, where it was shown that a hypothetical proposition may be translated into a categorical one; whence it follows that a Hypothetical Syllogism may be translated into a Categorical Syllogism. Treating the above examples thus, we find that the Modus ponens (with affirmative major premise) takes the form of Barbara, and the Modus tollens the form of Camestres:

Now if, instead of this, we affirm the consequent, to form the new minor premise,

This is a case of C being D,

there will be a Syllogism in the Second Figure with two affirmative premises, and therefore the fallacy of undistributed Middle. Again:

But if, instead of this, we deny the antecedent, to form the new minor premise,

This is not a case of A being B,

there arises a syllogism in the First Figure with a negative minor premise, and therefore the fallacy of illicit process of the major term.

By thus reducing the Hypothetical Syllogism to the Categorical form, what is lost in elegance is gained in intelligibility. For, first, we may justify ourselves in speaking of the hypothetical premise as the major, and of the categorical premise as the minor; since in the categorical form they contain respectively the major and minor terms. And, secondly, we may justify ourselves in treating the Hypothetical Syllogism as a kind of Mediate Inference, in spite of the fact that it does not exhibit two terms compared by means of a third; since in the Categorical form such terms distinctly appear: a new term ('This') emerges in the position of the minor; the place of the Middle is filled by the antecedent of the major premise in the Modus ponens, and by the consequent in the Modus tollens.

The mediate element of the inference in a Hypothetical Syllogism consists in asserting, or denying, the fulfilment of a given condition; just as in a Categorical syllogism to identify the minor term with the Middle is a condition of the major term's being predicated of it. In the hypothetical proposition—

If A is B, C is D—

the Antecedent, A is B, is the conditio sufficiens, or mark, of the Consequent, C is D; and therefore the Consequent, C is D, is a conditio sine qua non of the antecedent, A is B; and it is by means of affirming the former condition, or else denying the latter, that a conclusion is rendered possible.

Indeed, we need not say that the element of mediation consists in affirming, or denying, the fulfilment of a given condition: it is enough to say 'in affirming.' For thus to explain the Modus tollens, reduce it to the Modus ponens (contrapositing the major premise and obverting the minor):

The above four forms commonly treated of as Hypothetical Syllogisms, are called by Ueberweg and Dr. Keynes 'Hypothetico-Categorical.' Ueberweg restricts the name 'Hypothetical' simply (and Dr. Keynes the name 'Conditional') to such Syllogisms as the following, having two Hypothetical Premises: