Века сквозь математику, или Как математики раз за разом мир вертели

Екатерина Кукина

Века сквозь математику, или Как математики раз за разом мир вертели

Предисловие автора

В один прекрасный момент мне достался для прочтения курс лекций «История математики в контексте истории культур». Математик до мозга костей, я никогда не мыслила гуманитарными категориями, а уж тем более не читала гуманитарный курс. Математик с самого рождения и по сегодняшний день, я нуждаюсь в доказательстве всего и вся. Доказательства, принятые в классической истории, не всегда меня устраивают.

Для того, чтобы прилично прочитать курс /*а я думаю, мне это в итоге удалось*/ мне пришлось расширить сознание, перевернуть свое мышление вверх тормашками и приглушить внутренний голос, который постоянно из глубин подсознания нашептывает: «а почему именно так? а точно так, а не иначе?»

Итак, если вы тоже математик, я вам объясню, какова историческая основа моего курса. Мы, неспециалисты в истории, не задаемся вопросом: "А точно ли взятие Сиракуз, при котором умер Архимед, состоялось в 212 году до нашей эры? А как мы это датировали? А точны ли методы датировки?" Эти вопросы мы оставляем на откуп историкам-профессионалам. Если историки датируют папирус Ринда приблизительно 1650 годом до нашей эры, примем эту дату. /*В конце концов, позвольте профессионалам делать свое дело! Специализация – основа цивилизации.*/

Зачем вообще нужен на матфаке курс «История математики в контексте истории культур»? В этом курсе мы пытаемся проследить связь: как математика повлияла на историю и как наоборот история влияла на математику. Зачем? А затем, что математика способна изменить мир – и мы убедимся, что это не раз происходило уже в истории человечества.

Автор выражает глубокую признательность студентам, которые слушали курс, по мотивам которого возникла данная книжка. Невозможно передать то чувство, которое возникает у лектора, когда настроение в аудитории математиков и программистов от «История? Зачем нам вообще история?» меняется на «Вау! История – это интересно! А наши-то молодцы!» /*Спойлер: наши действительно молодцы! И "наши" – это, конечно же, математики.*/

Если честно, книг по истории математики опубликовано много: не одна, и даже не один десяток. А уж книг по истории… Чем же особенная эта? Я старалась сделать ее понятной среднему школьнику.

Наверное, зачастую, выкинув самую сердцевину математики, а оставив лишь истории про нее. И очень стремилась, чтобы книга вышла не занудной, не академической. Такой, какую приятно читать на ночь или в общественном транспорте. Наверное, это шло в ущерб точности и научности. Короче, я постараюсь просто рассказывать истории про историю и математику. И про то, как математика влияла на историю, а история на математику.

Вообще, оказывается, углубляться в историю математики – это очень-очень интересно, а порой – совершенно неожиданно. Вот, скажем, даже просто математическая генеалогия. Например, мой научный руководитель – Виталий Анатольевич Романьков. Его научный руководитель, а мой "научный дедушка" – Владимир Никанорович Ремесленников. Мой "научный пра-пра-пра-пра-дедушка" великий Павел Сергеевич Александров, а вот его "пра-пра-дедушка" – знаменитый Карл Вейерштрасс, научный внук самого Карла Гаусса, Короля математики. Таким образом, в моей прямой генеалогической научной линии встречаются все эти замечательные люди. Интересно? Мне кажется, очень1!

Клятвенно обещаю, что самое занудное в этой книге – данное предисловие.

А если вы нашли в книге опечатки, или хотите что-то обсудить, вы всегда можете прислать свои комментарии мне на электронную почту [e-mail]. Я все обязательно прочитаю, постараюсь опечатки исправить, и на вопросы по существу ответить.

Лекция 1

.

Доисторические времена

Глава, в которой математика еще почти не появляется. Только чуть-чуть.

Что такое "доисторические времена"? Все очень просто. Это времена, когда люди еще не изобрели письменность. И таким образом, не могли сами записывать свои истории. А вот когда мы уже можем прочитать о том, что творилось (как в «Повести временных лет», например) – это, соответственно, исторические времена.

Примерно 3 тысячи лет назад письменность уже точно появилась2.

Но некоторые элементы математических знаний появились раньше письменности. Вот об этих-то ранних предпосылках возникновения математики мы и поговорим в этой главе.

Что за ранние математические знания нас интересуют? Во-первых, это числа. Во-вторых, это геометрические фигуры. В-третьих, это другие естественно-научные сведения (астрономические, например, которые способствуют возникновению и развитию прикладной математики). Ну, и в главных – абстрактное мышление. Для математики как ни для чего другого необходимо абстрактное мышление.

Счет возникает тогда, когда человек замечает, что между двумя баранами и двумя камушками есть что-то общее. А что общее? Это что-то – что-то очень неуловимое и, безусловно, абстрактное. Это число.

Геометрия возникает тогда, когда человек замечает, что между солнцем в небе и камнем на берегу моря есть что-то общее. Это что-то – снова что-то очень неуловимое – форма.

Математика возникает тогда, когда человек перестает думать про конкретные объекты, а начинает думать про что-то неуловимое.

Итак, появился человек.

Рисунок 1.1: Иллюстрация из конспекта лекций

моей студентки Ангелины Андрейченко.

От австралопитеков (которые еще не "люди") произошли самые древние люди около 2,5 миллионов лет назад – человек Умелый, а позже из него Прямоходящий. В процессе эволюции люди учатся ходить на прямых ногах, не опираясь на руки. /*Что позволяет им смотреть иногда не в землю, а на звезды! – что для нас намного существеннее в контексте математики.*/ Кисть руки трансформируется, что выражается в противопоставлении большого пальца. /*Что позволяет нам теперь ловко держать ручку, кисточку и умело орудовать смартфоном одной рукой.*/ Ну, и самое главное – в процессе эволюции увеличивается мозг.

/*Кстати, забавный факт. Сначала примерно 2 миллиона лет эволюции мозг увеличивался и увеличивался. А вот последние 25 тысяч лет мозг человека уменьшается. Наш мозг процентов на 10 меньше, чем мозг Неандертальца и современного ему нашего предка, Человека Разумного. Ученые ушли думать и спорить, почему так.

А мозг женщин чуть-чуть меньше (процентов на 10) мозга мужчин. Наверное, потому, что женщины уже ушли еще дальше по лестнице эволюции.*/

Когда возникли люди, которые "Человек разумный разумный" (Homo Sapiens Sapiens)? То есть те люди, которые с биологической точки зрения уже как человек современный?

Если верить генетикам, человек разумный возник примерно 200 тысяч лет назад. Точнее, не так. "Ева" (самка, которая является предком всех ныне живущих людей) жила примерно 200 тысяч лет назад. А "Адам" (самец, который является предком всех ныне живущих людей) жил примерно 60 тысяч лет назад. /*Вот она – самая грустная история любви! А вы говорите: Ромео и Джульетта…*/ Примерно 68-ю тысячами лет датируются первые скелеты, которые можно отнести к Homo Sapiens. Один из самых древних (ему 45 тысяч лет) известных скелетов Homo Sapiens – Усть-Ишимский человек, найден /*минутка патриотизма!*/ на территории Омской области. Что говорит нам о том, что 45 тысяч лет назад люди разумные не просто возникли, а уже и расселились по территории Сибири. (Возникли они, все же, где-то на территории Африки).

Так когда же у людей появляются первые математические знания?

Пока люди не перешли от собирательства пищи и обычной охоты к активному производству (пищи, одежды, инструментов труда), они мало чем отличались от других видов млекопитающих. Их знания в математике и других науках никак не росли. Но в какой-то момент человек начал задумываться. О подобии форм. О производстве пищи. О выпасе скота. Эти процессы начались и пошли примерно одновременно.

Первые признаки абстрактного мышления, первые признаки воображения, можно отнести к возникновению наскальной живописи. А это примерно 35 тысяч лет назад. Знаменитые пещеры Альтамира в Испании и Ласко во Франции хранят великие картины тех времен3.

К этому же периоду относятся найденные фигурки животных и людей. А также инструменты труда, украшенные узорами. Абстрактными узорами и даже периодическими орнаментами.

Поразительны примеры не просто абстрактных узоров. Абстрактные узоры – свидетельства абстрактного мышления и того, что человек тех времен знал понятие формы – но примеры явно осознанных, обдуманных попыток зафиксировать некоторые данные.

Первые такие попытки появляются на дордонийской дощечке, которой примерно 30 тысяч лет (подробнее можно прочитать в [2]), очень знаменитой вестоницкой кости примерно того же возраста, Ачинском жезле, которому примерно 20 тысяч лет, и который найден в Сибири (подробнее про него можно почитать в [4]), и прочие, прочие, прочие доисторические артефакты.

Зарубки на этих артефактах не похожи на случайные или художественные. Они похожи на запись каких-то данных. Скорее всего, и дордонийская дощечка, и ачинский жезл – примеры календарей.

И явно, люди к этому моменту как минимум умели считать!

Даже одна из самых масштабных, древних и загадочных построек доисторических времен – Стоунхендж4 – по мнению ученых, скорее всего, ни что иное как древний календарь. Совершенно точно, что его конструкция соответствует многим астрономическим явлениям. Вот какие усилия вкладывали древние люди для того, чтобы познать природу.

Теория возникновения письменности.

Люди живут общиной, и пастух ведет баранов на пастбище. Как мы узнаем, что он всех привел обратно? Для этого брали сосуд, а в сосуд бросали камушки по количеству баранов. И когда пастух приводил баранов обратно, можно было свериться. /*И это, как сказали бы математики, – установление взаимно-однозначного соответствия между множествами баранов и камушков.*/ Но это рождало некоторый простор для махинаций. А вдруг пастух забрал камушек из сосуда? А вдруг кто-то подложил камушек в сосуд? Поэтому сосуд закупоривали. Но как тогда узнать количество камушков в нем, не разбивая? А очень просто – написать на боку!

И знаете, к какой мысли мы подходим вплотную? Именно числа стали скорее всего первым, что осмысленно писали люди. Сосуд, а на боку число 25 и нарисован бык – вот тебе и 25 быков ушло в поле. А уже потом изображение быка для скорости трансформировалось в букву "Алеф", постепенно превратившуюся в букву А.

Оказывается (и это уже не домысливания, а исторический факт), самые ранние примеры осмысленных записей имеют то или иное отношение к математике. Более того, сейчас практически установлено историками, что древняя письменность рождалась именно так – из необходимости писать числа. Была не полна, с помощью нее нельзя было описывать чудные мгновенья или великолепные виденья, а также уходящие вдаль тополиные аллеи. А рождалась письменность именно из необходимости писать числа. Вести бухгалтерию, если угодно (бухгалтерия, кстати, отделилась от математики в Средние века и с тех пор это две очень разные области знаний – но до того бухгалтерия, конечно, была областью прикладной математики).

Таким образом, нужды в математике (пусть, в той, примитивной доисторической математике, в умении просто считать) рождают письменность. Не потребность написать Иллиаду, не потребность соблазнить женщину прекрасной песней, нет. "Сухие" числа и счет. И не говорите после этого, что математика не влияет на историю человечества!

Итак, в каких математических знаниях доисторического человека мы можем быть уверены? Доисторический человек начал абстрактно мыслить. Возникли представления о форме. Доисторические люди изобрели круг и колесо (и не только). Доисторические люди вытачивали камни в виде правильных платоновых тел, или даже изготавливали их из бронзы. Они начали не то, что изобретать и изготавливать орудия труда, но и начали делать некоторые совершенно фантастические инженерные вещи. Например, построили Стоунхендж, вытесали статуи на острове Пасхи, вообще создавали очень большое количество украшений и статуэток…

Люди, очевидно, начали мыслить, находить параллели и закономерности. Совершенно точно, наблюдали за Луной, за Солнцем и другими астрономическими объектами (в частности, уже отличали на звездном небе планеты от звезд).

И, конечно, люди научились считать. Можно даже прикинуть, когда примерно возник у человечества счет. В некоторых языках числительные очень похожи. Один-два-три в русском. Viens-divi-tris на латышском. One-two-three в английском. Eins-zwei-drei на немецком. Uno-dos-tres на испанском. Очень близкие по звучанию слова, не так ли? /*Но, заметьте, близкие по звучанию, но не по написанию!*/ Но если мы возьмем эти же слова на грузинском (эрти-ори-сами), или на китайском (и-эр-сэн), или на венгерском (эг-кет-хааром) или икси-какси-колме на финском – то эти слова уже совершенно другие, не похожие на наши один-два-три. Это показывает нам, что считать люди научились до разделения языков германской и славянской групп, но, скажем, после разделения ностратических языков. Что позволяет прикинуть, что осознанный счет возник позже десятого, но ранее пятого тысячелетия до нашей эры. /*Но это не точно. И, конечно, у разных народов чуть-чуть по-разному.*/

Какие книги можно еще почитать.

К главе 1 про доисторическую математику.

[1]

C. Дробышевский, Достающее звено, в 2 томах. – М.: Издательство АСТ, 2017.

/*Достаточно современная книга, написанная очень живым и понятным языком, хотя и с хорошим уровнем научности и академизма.*/

[2]

Т. Придо, Кроманьонский человек. – М.: Мир, 1979.

/*Старенькая уже книжка, некоторые исторические факты, изложенные в ней, уже уточнены (читай: неправильные). Однако, очень интересная, хорошо написанная и с большим количеством иллюстраций.*/

[3]

Э.Уайт, Д.Браун, Первые люди. – М.: Мир, 1978.

/*Книжка из той же серии «Возникновение человека», что и [2], всего в той серии про доисторическую историю было 5 книг. Все классные, люблю их с детства (но именно эти две относятся к истории уже людей, а не до людей). Написаны все пять книг хорошо и с большим количеством иллюстраций. Рекомендую.*/

[4]

В. Ларичев, Пещерные чародеи. – Новосибирск: Западно-сибирское книжное издательство, 1980 год.

/*Книжка забавная. Популярная, с некоторым налетом эпатажа, но интересная, написана Виталием Ларичевым, академиком РАЕН, известным ученым, археологом, антропологом, востоковедом.*/

[5]

Д. Стройк, Краткий очерк истории математики. – М.:Наука, 1990.

/*Это очень нескучная книга по истории математики. Гораздо менее популярная, чем то, что вы читаете сейчас, но гораздо более полная (ну, в смысле, там больше всего понаписано).*/

[6]

под ред. А. П. Юшкевича, «История математики с древнейших времен до начала XIX столетия» в 3 томах, т.1. – М.:Наука, 1970.

/*«История математики» Юшкевича – это уже вообще серьезная книга по истории математики, можно ее считать в некотором роде учебником по истории математики. Она написана не так забавно и занимательно, как все предыдущее, но зато гораздо более "академическая". Если вам именно этого не хватает в моей книжке – пожалуйста. Но надо учитывать, что некоторые данные из книги несколько устарели.*/

Лекция 2

.

Математика до возникновения математики

В некоторых частях света письменность возникла раньше, в других позже. Нас сейчас интересуют самые древние (из известных) письмена древних людей. А это – глинобитные таблички Междуречья (3,5 тысячи лет до н.э.) и папирусы Древнего Египта (около 2,4 тысяч лет до н.э.). Неоспоримые исторические свидетельства того, что математика тогда уже была.

Понятно, что письменность в те времена была делом дорогим (а также чисто технически долгим и трудным). Записывали только самое-самое важное. Самое-самое необходимое. И среди прочего – математические трактаты.

Почему я назвала эту главу "математика до возникновения математики"? Потому что математикой уже начали заниматься, начали копить некоторые математические знания, но собственно наука математика еще не возникает – она появится позже, в Древней Греции. И это, вообще-то, нормально. Чтобы возникла наука, ей нужен объект изучения. Астрономия возникла, когда уже были звезды. Анатомия – когда уже был человек. Так и тут. Многие занимались математикой еще до того, как это стало мейнстримом (и даже появилось такое слово!)

Итак, что же мы можем почерпнуть из ископаемых манускриптов?

2.1

Древний Египет

В Древнем Египте занимались математикой так называемые писцы. Они были чиновниками при египетских царях (фараонах). Передавали их указы военноначальникам, указывали рабам, как строить здания, рассчитывали налоги. (Т.е. вообще-то обладали очень большой властью и были людьми уважаемыми). Для всего этого им требовались знания математики.

Самый известный в мире математический папирус – папирус Ринда. Он около 32 сантиметров в ширину и более 5 метров в длину (2 куска длиной 3 метра и 2 метра хранятся в Британском музее; и еще кусок около 18 сантиметров утерян в веках). Этот папирус целиком посвящен разным математическим задачкам. Написан писцом по имени Ахмес примерно в 1650-м году до нашей эры. Но считается, что Ахмес переписывал его с еще более древнего манускрипта.

Самый древний из известных математических папирусов – Московский математический папирус, он написан около 1850 года до нашей эры. (Хранится в музее изобразительных искусств им.А.С.Пушкина).

/*Вы когда-нибудь обращали внимание, что самые интересные египетские папирусы хранятся вовсе не в Египте? Как и самые известные глинобитные вавилонские таблички вовсе не в Ираке.*/

Древние математические папирусы служили своеобразными учебниками математики – именно по ним изучали эту премудность новые писцы.

Итак, какого рода задачи можно встретить в папирусах? В папирусе Анастаси номер 1 читаем:

«Я ставлю тебя в тупик, когда приношу тебе повеление от твоего господина, тебе – его царскому писцу, поставленному во главе войска. Должно сделать насыпь для подъема в 730 локтей длины и 55 локтей ширины; она состоит из 120 отдельных ящиков и покрывается перекладинами и тростником. На верхнем конце она имеет высоту в 60 локтей, а в середине 30 локтей; уклон ее – дважды по 15 локтей, а настил – 5 локтей. Спрашивают у военачальников, сколько понадобится кирпичей, и у всех писцов, и ни один ничего не знает. Все они надеются на тебя и говорят: "Ты искусный писец, мой друг, сосчитай это для нас поскорей. Смотри, имя твое славится. Сколько же надо для этого кирпичей?"»

И вот такого рода задачи приходится решать. А куда деваться?

/*К счастью, современным математикам подобные задачи встречаются последний раз приблизительно в школе. Современные математики вообще не решают задачи с числами, только с буквами и прочими непонятными закорючками, типа ∫, ▽ или ↘. Помочь в вызове дьявола эти письмена то ли способны, то ли нет, но чтобы придать им какой-либо практический смысл обычно требуется примерно 200 лет.*/

Числа египтяне записывали похоже на известные нам римские числа. Единицы – палочки. Десяток объединяли в символ в виде подковы. Сотню в символ в виде завитка. И так далее. Были символы для тысячи, десяти тысяч, сотни тысяч, миллиона. То есть система счисления у них десятичная, но цифры и, соответственно, позиционная запись числа еще не появляются. (Единицы, кстати, слева, потом десятки и т.д.). В такой системе записи удобно числа складывать (все символы записываем вместе, при необходимости 10 символов одного вида меняем на следующий). И удобно числа умножать на 2 (складывая само с собой). Вычитать (меньшее из большего, конечно) – тоже вполне легко. А большее из меньшего вычитать им не могло и в голову прийти!

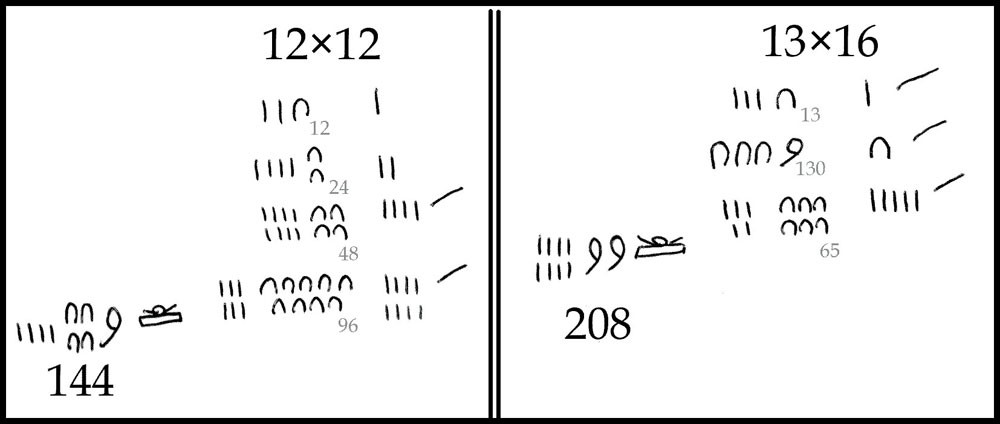
Рисунок 2.1: Два примера на умножение из папируса Ринда

А вот как египтяне умножали числа. (См.рис.2.1) Они число удваивали несколько раз и записывали результаты. В правой колонке – на что уже умножили. В левой – результат. Так удваивали до тех пор, пока сумма некоторых чисел в правом столбце не даст второй сомножитель. И складывали соответствующие числа из левой колонки.

Левый пример на рисунке как раз иллюстрирует такую типичную запись. Нам нужно посчитать 12 × 12. Удваиваем 12 несколько раз.

121=12, 122=24, 124=48, 128=96.

Тут мы замечем, что 12=4+8 (12 – число, на которое нам надо умножить; 4 и 8 – на которые мы уже умножили), и поэтому результат умножения получится 48+96=144.

Как мы видим, умножать – не такой уж легкий труд! А кроме того, египтяне при умножении фактически пользовались и двоичной записью числа.

Но иногда можно было использовать умножение на 10 сразу. На 10 ведь умножать легко. Просто все символы заменить на бóльшие. И тогда еще можно умножить на пять (поделить удесятеренное число пополам).

Правый пример на картинке как раз иллюстрирует атипичную запись, использует умножение на 10 и на 5. Нам нужно посчитать 13×16.

131=13, 1310=130, 135=65.

Поскольку 16=10+5+1, то результат умножения 130+65+13=208.

/*При таком умножении очевидно, что коммутативность умножения (то есть то, что от перестановки мест сомножителей произведение не меняется) – штука дааааалеко не очевидная! Чтобы ее заметить, надо быть очень опытным писцом. Практически, математическое открытие!*/

Как писцы выбирали метод умножения – неизвестно. Почему на 16 приведен пример в папирусе с умножением на 10 и на 5 (а не 4 раза удвоение) – непонятно. Почему на 12 нельзя было умножить на (10+2) – непонятно. То есть, никакого четкого алгоритма в их действиях, вообще говоря, не было. Хорошо, что умножение – это вам не бином Ньютона, все не мытьем так катаньем получалось рано или поздно. В папирусах, собственно, ничего не объяснялось. Просто разбирались примеры. /*Делай так, и будет тебе счастье!*/

Рисунок 2.2: Пример на деление из папируса Ринда

/*А попробуйте сами для прикола произвести какие-нибудь умножения по-египетски. Ну, напирмер, 23 на 25. Спорим, в процессе вам волей-неволей захочется воскликнуть что-то типа: «Да, ёшкин кот, египетский бог!»*/

Обратите внимание также на закорючку в виде закрытого и запечатанного списка (возможно, именно она позднее трансформировалась в символ равенства) – она ставится перед ответом и означает, что вычисление, собственно, выполнено. Свиток запечатан, получите, распишитесь.

Ох, как же сложно все с делением! Вы же уже представили? Деление – операция обратная умножению. Т.е., например, надо вам поделить число 1120 на 80. (См. рисунок 2.2) Иными словами, вы должны подобрать множитель, который при умножении на 80 даст 1120. Подбираем. Умножаем 80 на 2 несколько раз. На 16 умножать смысла уже нет (т.к. получится 1280, что больше нужного нам 1120). На всякий случай умножаем и на 10 (потому что легко же!). Замечаем, что числа 800 и 320 из левой колонки дают нужный ответ 1120. Таким образом, результат деления 14. (Однако после знака "равно" писали все равно 1120. По форме записи пример на деление ничем не отличался от примера на умножение!)

Рисунок 2.3: Фрагмент Папируса Ринда.

Но самые заморочки начинались у египтян с дробями. Они признавали только дроби с числителем 1. Были и сложные дроби, которые составлялись как сумма нескольких обязательно разных простых дробей (с числителем 1). Сейчас такие дроби в математике так и называются "египетские дроби". Записывали они дроби в виде лунки над натуральным числом (фактически, только знаменатель, ведь числитель – всегда 1).