Психотроника и днк. Искусственный интеллект в битве со старением организма человека. Психотроника и днк

Но элементы, из которых строятся нити нуклеиновых кислот, могут быть устроены во многих различных последовательностях, и нить шаблона может отделиться от копии. И нить, и её копия могут далее снова быть скопированы. Представьте себе нить РНК, плавающую в испытательной пробирке вместе с копировальными машинами и элементами РНК. Нить кувыркается и изгибается, пока она не наталкивается на копировальную машину в правильном положении, чтобы слипнуться. Элементы толкутся вокруг, пока один нужного вида не встретит копировальную машину в правильном положении, которая соответствует нити шаблона. Как только соответствующие элементы ухитряются попасть в нужное положение, машина захватывает их и привязывает их к растущей копии; хотя элементы сталкиваются случайным образом, машина связывает выборочно. В конце концов, машина, шаблон и копия разъединяются.

История жизни – история гонки вооружения на базе молекулярных машин. Сегодня, в то время как эта гонка подходит к новой и более быстрой стадии, мы должны убедиться, что мы понимаем только, насколько глубокие корни имеет эволюция. Во времена, когда идеей биологической эволюции часто пренебрегают в школах, и она иногда подвергается нападкам, мы должны помнить, что доказательства её прочны как скала и также распространены, как клетки. В течение столетий геологи изучали камни, чтобы читать прошлое Земли. Уже давно они нашли морские раковины высоко в разрушившейся и рухнувшей скале горных цепей. К тысяча семьсот восемьдесят пятому году, за семьдесят четыре года до ненавистной книги Дарвина, Джеймс Хуттон заключил, что грязь с морского дна была спрессована в камень и была поднята к небесам силами, пока ещё не понятными. Что ещё могли думать геологи, если сама природа врала?

Каменная книга делает запись форм давно умерших организмов, однако живые клетки также несут записи, генетические тексты, которые только теперь могут быть прочитаны. Так же как с идеями о геологии, наиболее важные идеи относительно эволюции были известны прежде, чем Дарвин взял в руки перо.

Гены походят на рукописи, написанные в четырёхбуквенном алфавите. Во многом так же, как сообщение может принимать много форм на обычном языке (выразить идею с использованием совершенно различных слов не слишком трудно), так же различные генетические слова могут направить строительство идентичных белковых молекул. Более того, белковые молекулы с различными особенностями устройства могут выполнять одинаковые функции. Совокупности генов в клетке подобны целой книге, а гены – подобны старым рукописям, они копировались и копировались неаккуратными переписчиками.

Глобальная гонка технологий ускорялась в течение миллиардов лет. Слепота земляного червя не могла блокировать развитие зорких птиц. Маленький мозг и неуклюжие крылья птицы не могли блокировать развитие человеческих рук, умов и стреляющих ружей. Аналогично, местные запреты не могут блокировать развитие военной и коммерческой технологии. По- видимому, мы должны управлять гонкой технологий или умереть, однако сила технологической эволюции делает из анти технологических движений посмешище: демократические движения за местные ограничения могут ограничить только мировые демократии, но не мир в целом. История жизни и потенциал новых технологий подсказывают некоторые решения.

Человеческий разум, однако, намного более тонкая машина имитации, чем любая простая белковая машина или ассемблер. Голос, письмо и рисунок могут передать конструкции из разума к разуму прежде, чем они примут форму как аппаратные средства. Идеи, стоящие за методами разработки, ещё более тонкие: более абстрактные, чем аппаратные средства, они копируются и функционируют исключительно в мире разума и систем символов. Там, где гены эволюционировали в течение поколений и эпох, мысленные репликаторы пока эволюционируют в течение дней и десятилетий. Подобно генам, идеи расщепляются, объединяются и принимают многообразные формы (гены могут быть расшифрованы из ДНК в РНК и снова использованы; идеи могут быть переведены с языка на язык). Наука не может пока описать нейронные структуры, которые воплощают идеи в мозгу, но любой может видеть, что идеи мутируют, воспроизводятся и конкурируют. Идеи подвержены эволюции.

Элементы воспроизводящихся мысленных структур называются «мимами» (англ. «тете»). Примеры мимов – мелодии, идеи, общеупотребительные выражения, мода в одежде, способы производства горшков и постройки арок. Так же, как гены размножаются в среде генов, перескакивая от тела к телу (от поколения к поколению) через сперму или яйца, так же и мимы размножаются в среде мимов, перескакивая из мозга в мозг посредством процесса, который в широком смысле может называться имитацией.

Мимы копируются, потому что люди учатся и учат других. Они изменяются, потому что люди создают новые и неправильно истолковывают старые. Они подвергаются селекции (отчасти), потому что люди не верят или повторяют все, что слышат. Так же как молекулы РНК из испытательной пробирки конкурируют за ограниченные в количестве копировальные машины и строительные элементы, мимы должны конкурировать за ограниченный ресурс – человеческое внимание и усилия. Так как мимы формируют поведение, их успех или неудача – это жизненно важный вопрос. Так же как вирусы мимы научились побуждать клетки производить вирусы, так же слухи научились звучать правдоподобно и пикантно, побуждая повторение. Спросите, не является ли слух правдой, а как он распространяется. Опыт показывает, что идеям, научившимся быть успешными репликаторами, нужно иметь лишь очень немного от правды.

Принципы эволюционного изменения, имеющие глубокие корни, будут формировать развитие нанотехнологии, даже когда различие между аппаратными средствами компьютеров и жизнью начнёт стираться. Эти принципы показывают многое из того, что мы можем и не можем надеяться достичь, и они могут помочь нам сконцентрировать наши усилия, чтобы формировать наше будущее. Они также говорят нам много о том, что мы можем и не можем предсказать, потому что они управляют эволюцией не только материального, но и эволюцией самого знания.

Что мы знаем о мутации ДНК?

Жизнь кажется нам (живым) каким-то особенным феноменом среди прочих природных явлений. Однако, присмотревшись, можно увидеть в такой позиции всего лишь жизнецентризм. Эволюция видов происходит благодаря накоплению устойчивых форм, которое действует и в неживой природе. Основа земной жизни, набор хромосом в живой клетке, изобреталась природой миллиард лет. После этого жизнь оккупировала Землю и стала практически неистребимой. Устойчивость такого химического объекта, как ДНК обеспечивается её способностью к самокопированию при наличии подходящего для построения копий биохимического материала. Наверно, вначале природа изобрела не ДНК, а некую пока не реконструированную химическую реакцию копирования. С её открытием началась цепная реакция удвоения количества нового химического вещества. На огромное количество этого вещества начал действовать естественный отбор, результатом которого стало построение предка молекулы ДНК вместе с её средой обитания – клеткой. За миллиарды лет эволюция выработала только одно вещество, способное к самокопированию. ДНК вместе с соответствующей данному виду клеткой есть результат борьбы химических форм за устойчивость. То, что оказалось не устойчивым, исчезло. Устойчивость (жизнеспособность) определённого вида ДНК обеспечивается тем, что соответствующая клетка и организм способны обеспечить себе условия для выполнения копирования. Процесс деления клетки начинается тогда, когда имеются в наличии практически все химические материалы, необходимые для построения копии ДНК.

Если поступление этих материалов в клетку задерживается, то процесс копирования ДНК приостанавливается вплоть до гибели клетки. Известно, каким образом в ДНК закодировано производство белков. Но как информация о форме и образе жизни живого существа, может быть выведена из кодировки ДНК? Клетка и живое существо – это биологические формы, способствующие устойчивости определённого набора хромосом. Конечно, удобнее и уместнее говорить об устойчивости вида живых существ. Живой организм, возникший как колония клеток определенного вида, призван своей жизнедеятельностью обеспечить себя, то есть каждую клетку колонии, необходимым химическим материалом в нужных пропорциях. Раз уж это важно для выживания, то необходимо учитывать и интересы своих соплеменников. Именно это является причиной формирования определенного вида с его поведением и формой. Вместе с модификацией вида, способствующей его устойчивости, модифицируется и набор хромосом. Некоторые виды в такой борьбе изменяются и становятся сильнее. Другие вымирают. Итак, хранящуюся в ДНК программу производства белков можно интерпретировать как информацию о том наборе химических веществ, который необходим для деления клетки. Эта информация очень опосредованно связана с формой и поведением живого существа. Большое количество элементов в ДНК позволяет выполняет тонкую регулировку химического состава клетки. В зависимости от деятельности окружающих клеток, то есть от окружающих химических и механических воздействий, клетка изменяет свою жизнь так, чтобы приобрести необходимые вещества для построения копии набора хромосом.

Это особенно заметно на этапе морфогенеза. Вот почему у живых существ формируются ткани и органы, выполняющие химические, механические и другие функции для обеспечения выживания вида. Механизм морфогенеза существенно использует саморегулирование активности ДНК в зависимости от биохимического состава клетки. Изменение молекулы ДНК, например, в результате мутации, приводит к изменению жизнедеятельности и условий деления клетки. Если в результате деления такой клетки был построен живой организм, то каждая клетка организма содержит копию изменённой молекулы ДНК, что должно отразиться на функциях (и даже анатомии) всех тканей и органов. Изменения функций одних органов может оказаться малозаметным, а других – сильным, вплоть до полного нарушения их нормальной работы. Это может выглядеть как изменение каких-либо существенных признаков живого организма. Поскольку каждый ген управляет синтезом определённого белка, а ассортимент белков не велик, то генетическое изменение может наблюдаться, как «включение» или «отключение» определённой функции или признака организма. Однако, поскольку одинаковые ДНК содержатся во всех клетках организма, то в общем случае, изменение ДНК должно влиять на все функции организма. ДНК не может содержать участков (генов), отвечающих строго за один признак. Тем не менее, модификация некоторых «генов» может привести к «полезным» изменениям организма.

Генетические алгоритмы – это мощный инструмент для решения сложных задач. Они нашли применение в оптимизации, искусственном интеллекте, инженерии и других областях. В основе генетических алгоритмов лежат принципы, заимствованные из биологии и генетики. Напомним: основная идея генетических алгоритмов состоит в создании популяции особей (индивидов), каждая из которых представляется в виде хромосомы. Любая хромосома есть возможное решение рассматриваемой оптимизационной задачи. Для поиска лучших решений необходимо только значение целевой функции, или функции приспособленности. Значение функции приспособленности особи показывает, насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи. Хромосома состоит из конечного числа генов, представляя генотип объекта, т.е. совокупность его наследственных признаков. Процесс эволюционного поиска ведется только на уровне генотипа. К популяции применяются основные биологические операторы: скрещивания, мутации, инверсии и др. В процессе эволюции действует известный принцип «выживает сильнейший». Популяция постоянно обновляется при помощи генерации новых особей и уничтожения старых, и каждая новая популяция становится лучше и зависит только от предыдущей. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены теоретические результаты о целесообразности использования именно двоичного алфавита. К тому же, реализация такого генетического алгоритма на ЭВМ была сравнительно легкой.

Все же, небольшая группа исследователей шла по пути применения в генетических алгоритмах отличных от двоичных алфавитов для решения частных прикладных задач. Одной из таких задач является нахождение решений, представленных в форме вещественных чисел, что называется не иначе как «поисковая оптимизация в непрерывных пространствах».

Возникла следующая идея: решение в хромосоме представлять напрямую в виде набора вещественных чисел. Естественно, что потребовались специальные реализации биологических операторов. Такой тип генетического алгоритма получил название непрерывного генетического алгоритма, или генетического алгоритма с вещественным кодированием.

Далее в тексте по аналогии с англоязычной терминологией для генетических алгоритмов с двоичным кодированием будет использоваться аббревиатура BGA (Binary coded), для генетических алгоритмов с непрерывными генами – RGA (Real coded).

Преимущества и недостатки двоичного кодирования

Прежде чем излагать особенности математического аппарата непрерывных генетических алгоритмов, остановимся на анализе достоинств и недостатков двоичной схем кодирования. Как известно, высокая эффективность отыскания глобального минимума или максимума генетическим алгоритмом с двоичным кодированием теоретически обоснована в фундаментальной теореме генетических алгоритмов («теореме о шаблоне»), доказанной Холландом.

Ее подробное освещение и доказательство можно найти в соответствующих источниках. Ее суть в том, что двоичный алфавит позволяет обрабатывать максимальное количество информации по сравнению с другими схемами кодирования. Однако двоичное представление хромосом влечет за собой определенные трудности при поиске в непрерывных пространствах большой размерности, и когда требуется высокая точность найденного решения. В BGA для преобразования генотипа в фенотип используется специальный прием, основанный на том, что весь интервал допустимых значений признака объекта [ai, bi] разбивается на участки с требуемой точностью. Заданная точность р определяется выражением

где N – количество разрядов для кодирования битовой строки.

Эта формула показывает, что р сильно зависит от N, т.е. точность представления определяется количеством разрядов, используемых для кодирования одной хромосомы. Поэтому при увеличении N пространство поиска расширяется и становится огромным.

Известный книжный пример: пусть для 100 ста переменных, изменяющихся в интервале [-500; 500], требуется найти экстремум с точностью до шестого знака после запятой. В этом случае при использовании генетических алгоритмов с двоичным кодированием длина строки составит 3000 три тысячи элементов, а пространство поиска – около Ю1000 хромосом.

Эффективность BGA в этом случае будет невысокой. На первых итерациях алгоритм потратит много усилий на оценку младших разрядов числа, закодированных во фрагменте двоичной хромосомы. Но оптимальное значение на первых итерациях будет зависеть от старших разрядов числа. Следовательно, пока в процессе эволюции алгоритм не выйдет на значение старшего разряда в окрестности оптимума, операции с младшими разрядами окажутся бесполезными. С другой стороны, когда это произойдет, станут не нужны операции со старшими разрядами – необходимо улучшать точность решения поиском в младших разрядах.

Такое «идеальное» поведение не обеспечивает семейство алгоритмов BGA, т.к. эти алгоритмы оперируют битовой строкой целиком, и на первых же эпохах младшие разряды чисел «застывают», принимая случайное значение. В классических генетических алгоритмов разработаны специальные приемы по выходу из этой ситуации. Например, последовательный запуск ансамбля генетических алгоритмов с постепенным сужением пространства поиска.

Есть и другая проблема: при увеличении длины битовой строки необходимо увеличивать и численность популяции.

Как уже отмечалось, при работе с оптимизационными задачами в непрерывных пространствах вполне естественно представлять гены напрямую вещественными числами. В этом случае хромосома есть вектор вещественных чисел. Их точность будет определяться исключительно разрядной сеткой тем компьютером, на котором реализуется real-coded алгоритм. Длина хромосомы будет совпадать с длиной вектора-решения оптимизационной задачи, иначе говоря, каждый ген будет отвечать за одну переменную. Генотип объекта становится идентичным его фенотипу.

Вышесказанное определяет список основных преимуществ real-coded алгоритмов:

Использование непрерывных генов делает возможным поиск в больших пространствах (даже в неизвестных), что трудно делать в случае двоичных генов, когда увеличение пространства поиска сокращает точность решения при неизменной длине хромосомы.

Одной из важных черт непрерывных генетических алгоритмов является их способность к локальной настройке решений.

Использование RGA для представления решений удобно, поскольку близко к постановке большинства прикладных задач. Кроме того, отсутствие операций кодирования/декодирования, которые необходимы в BGA, повышает скорость работы алгоритма. Как известно, появление новых особей в популяции канонического генетического алгоритма обеспечивают несколько биологических операторов: отбор, скрещивание и мутация. В качестве операторов отбора особей в родительскую пару здесь подходят любые известные из BGA: рулетка, турнирный, случайный. Однако операторы скрещивания и мутации не годятся: в классических реализациях они работают с битовыми строками. Нужны собственные реализации, учитывающие специфику real-coded алгоритмов.

Оператор скрещивания непрерывного генетического алгоритма, или кроссовер, порождает одного или нескольких потомков от двух хромосом. Собственно говоря, требуется из двух векторов вещественных чисел получить новые векторы по каким-либо законам. Большинство real-coded алгоритмов генерируют новые векторы в окрестности родительских пар. Для начала рассмотрим простые и популярные кроссоверы.

Пусть С1= (с11,с21,…,сп1) и С2= (с12,с22,…,сп2) -две хромосомы, выбранные оператором селекции для скрещивания. После формулы для некоторых кроссоверов приводится рисунок – геометрическая интерпретация его работы. Предполагается, что ck1 <=ck2 и f (C1)> =f (C2).

Плоский кроссовер (flat crossover): создается потомок H= (h1,…,hk,…,hn), hk, k=l,…, п – случайное число из интервала [е^Ск2] *

Простейший кроссовер (simple crossover): случайным образом выбирается число к из интервала {1,2,…,п-1} и генерируются два потомка

Hl= (c11,c21,…,ck1,ck+12,…,cn2) и H2= (c12,c22,…,ck2,ck+11,…,cn2).

Арифметический кроссовер (arithmetical crossover): создаются два потомка H1= (h11,…,hn1), ^ (hi2,…,!^2), где hk1=w*ck1+ (l-w) *ck2, hk2=w*ck2+ (l-w) *ck1, k=l,…,n, w либо константа (равномерный арифметический кроссовер) из интервала [0;1], либо изменяется с увеличением эпох (неравномерный арифметический кроссовер).

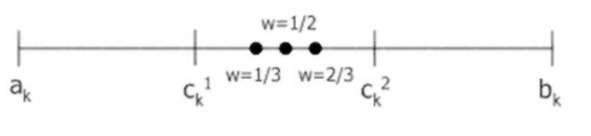
Геометрический кроссовер (geometrical crossover): создаются два потомка

H1=(hI‘,~..hn1), H2= (h,2, -,h„2), где hk> = (cklr* (ck2) lw, (ck2r* (ckl) lw, w – случайное число из интервала [0;1].

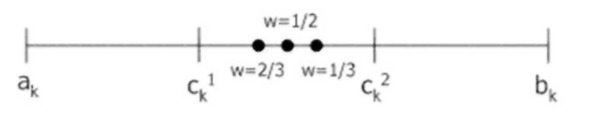
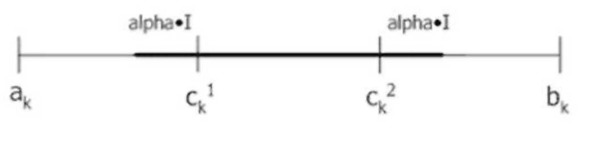
Линейный кроссовер (linear crossover): создаются три потомка Hq= (h1q,…,hkq,…,hnq), q=l,2,3, где hk1=0.5*ck1+0.5*ck2, hk2=1.5*ck1—0.5*ck2, hk3=-0.5*ck1+1.5*ck2. На этапе селекции в этом кроссовере отбираются два наиболее сильных потомка.

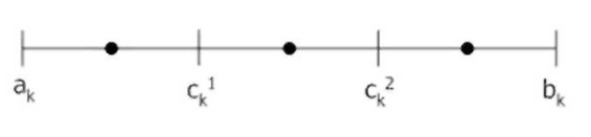
Дискретный кроссовер (discrete crossover): каждый ген hk выбирается случайно по равномерному закону из конечного множества {ц1,^2}.

Расширенный линейчатый кроссовер (extended line crossover): ген hk=ck1+w* (ck2“ck1b w “ случайное число из интервала [-0.25;1.25].

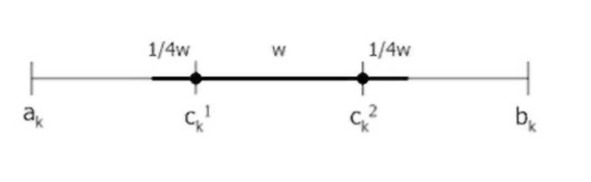
Эвристический кроссовер (Wright’s heuristic crossover). Пусть Cx – один из двух родителей с лучшей приспособленностью. Тогда hk=w* (ck1-ck2) +ck1, w- случайное число из интервала [0;1].

Нечеткий кроссовер (fuzzy recombination, FR-d crossover): создаются два потомка Нх= (h11,…,hn1), Н2= (h11,…/hn2). Вероятность того, что в i-том гене появится число v±, задается распределением p (v±) e {F (с^.1), F (ck2)}, где F (ck1), F (ck2) – распределения вероятностей треугольной формы (треугольные нечеткие функции принадлежности) со следующими свойствами (ck1 <=ck2 и 1= | с^-с^ |) :

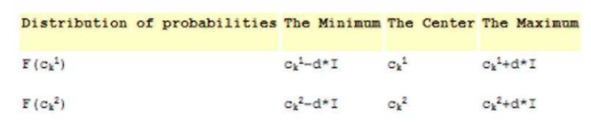
Параметр d определяет степень перекрытия треугольных функций принадлежности, по умолчанию d=0.5.

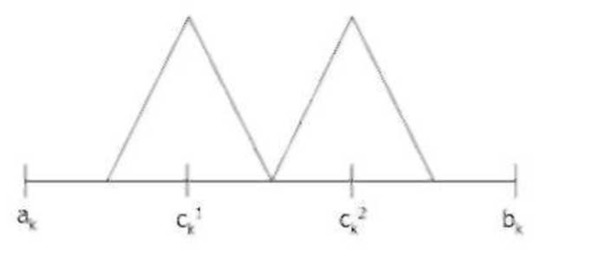
В качестве оператора мутации наибольшее распространение получили: случайная и неравномерная мутация (random and non-uniform mutation).При случайной мутации ген, подлежащий изменению, принимает случайное значение из интервала своего изменения. В неравномерной мутации значение гена после оператора мутации рассчитывается по формуле:

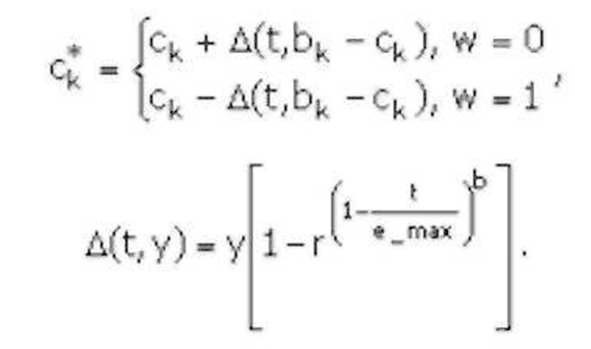
Сложно сказать, что более эффективно в каждом конкретном случае, но многочисленные исследования доказывают, что непрерывные генетические алгоритмы не менее эффективно, а часто гораздо эффективнее справляются с задачами оптимизации в многомерных пространствах, при этом более просты в реализации из-за отсутствия процедур кодирования и декодирования хромосом.

Рассмотренные кроссоверы исторически были предложены первыми, однако во многих задачах их эффективность оказывается невысокой. Исключение составляет BLX-кроссовер с параметром alpha=0.5-OH превосходит по эффективности большинство простых кроссоверов. Позднее были разработаны улучшенные операторы скрещивания, аналитическая формула которых и эффективность обоснованы теоретически. Рассмотрим подробнее один из таких кроссоверов – SBX.

SBX кроссовер

SBX (англ.: Simulated Binary Crossover) – кроссовер, имитирующий двоичный. Был разработан в тысяча девятьсот девяносто пятом году исследовательской группой под руководством Deb’a. Как следует из его названия, этот кроссовер моделирует принципы работы двоичного оператора скрещивания.

SBX кроссовер был получен следующим способом. У двоичного кроссовера было обнаружено важное свойство – среднее значение функции приспособленности оставалось неизменным у родителей и их потомков, полученных путем скрещивания. Затем автором было введено понятие силы поиска кроссовера (search power). Это количественная величина, характеризующая распределение вероятностей появления любого потомка от двух произвольных родителей. Первоначально была рассчитана сила поиска для одноточечного двоичного кроссовера, а затем был разработан вещественный SBX кроссовер с такой же силой поиска. В нем сила поиска характеризуется распределением вероятностей случайной величины $:

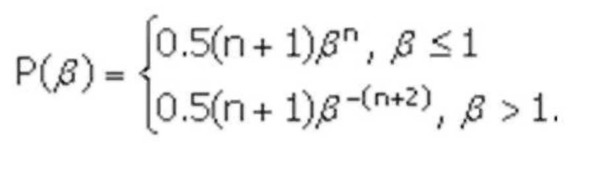
В

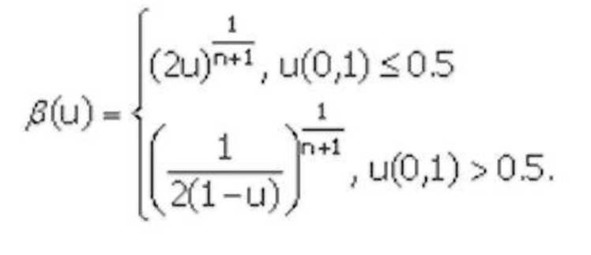
формуле и (0,1) – случайное число, распределенное по равномерному закону, пе [2,5] – параметр кроссовера.

На рисунке приведена геометрическая интерпретация работы SBX кроссовера при скрещивании двух хромосом, соответствующих вещественным числам 2 и 5. Видно, как параметр п влияет на конечный результат: увеличение п влечет за собой увеличение вероятности появления потомка в окрестности родителя и наоборот.

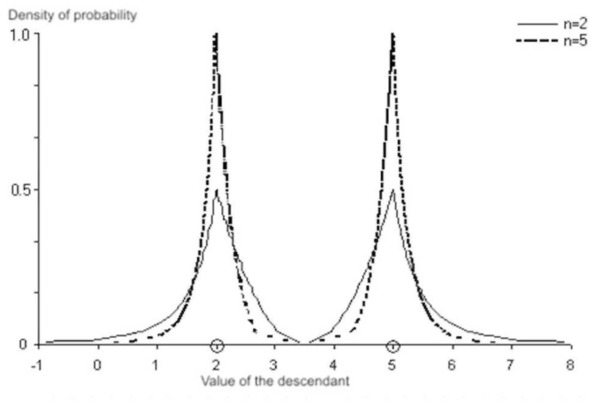
Эксперименты автора SBX кроссовера показали, что он во многих случаях эффективнее BLX, хотя, очевидно, что не существует ни одного кроссовера, эффективного во всех случаях. Исследования показывают, что использование нескольких различных операторов кроссовера позволяет уменьшить вероятность преждевременной сходимости, т.е. улучшить эффективность алгоритма оптимизации в целом. Для этого могут использоваться специальные стратегии, изменяющие вероятность применения отдельного эволюционного оператора в зависимости от его «успешности», или использование гибридных кроссоверов, которых в настоящее время насчитывается несколько десятков. В любом случае, если перед Вами стоит задача оптимизации в непрерывных пространствах, и Вы планируете применить эволюционные техники, то следует сделать выбор в пользу непрерывного генетического алгоритма. Особенности при создании индуктивной катушки