Ключевые технологии и приемы использования щитовых проходческих комплексов при сооружении туннелей

Во время обычной проходки щита степень фронтального и среднего оседания составила около 1.3 мм; во время прохождения 57-го звена на точке № 12 через радиальное отверстие щита был закачен заполнитель GMEM и пройдено 15 звеньев с заполнением вокруг корпуса щита, при этом показатели оседания контролировались на уровне 0.2 ~ 0.3 мм. Результаты измерения оседания пласта до и после использования заполнителя GMEM можно увидеть на рис. 3-22.

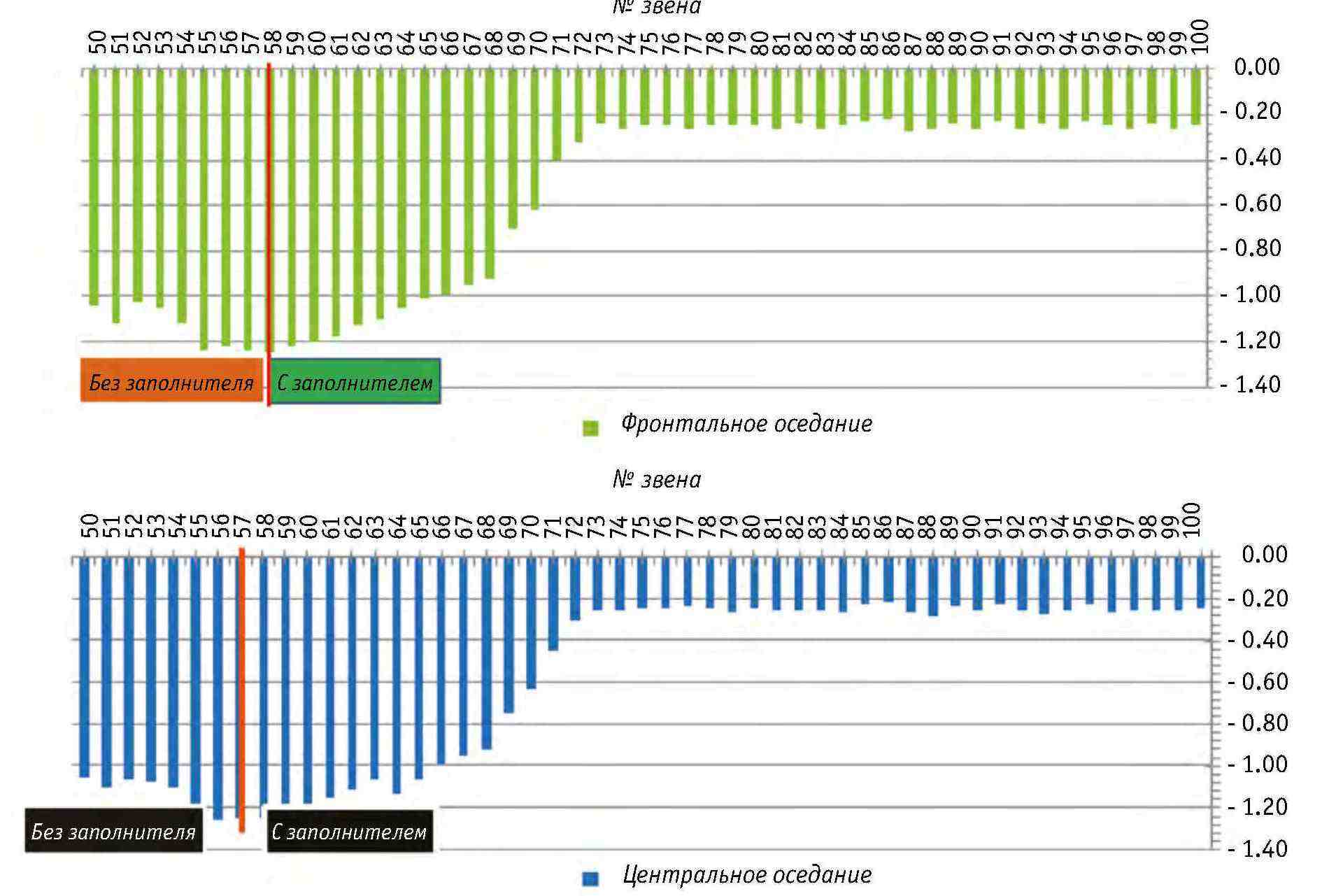
Рис. 3-22. Результаты измерений до и после использования заполнителя GMEM

ГЛАВА 4. ПРОЕКТИРОВАНИЕ ЩИТОВОЙ ОБДЕЛКИ ТУННЕЛЯ

Продуманная конструкция обделки щитового туннеля оказывает решающее влияние на качество всего туннеля после формовки. В отрасли существуют разногласия по поводу водонепроницаемости стыков труб, использования однослойной или двухслойной обделки для щитовых туннелей и т. д. В данной главе приводятся некоторые соображения по этим вопросам в сочетании с инженерной практикой.

4.1. КОНСТРУКЦИЯ ТЮБИНГА

Как в отечественной, так и в международной практике при проектировании щитовых туннелей основное внимание уделяется безопасности, экономичности и применимости при монтаже. Проектирование тюбингов осуществляется как в поперечном, так и в продольном направлениях туннеля. Обычно проектирование в первом случае определяет поперечное сечение туннеля, а проектирование во втором – способность туннеля противостоять землетрясениям и оседанию основания. В данном разделе обобщаются и сравниваются методы проектирования, модели тюбинга, сейсмостойкость тюбинга и армирование тюбинга щитового туннеля.

4.1.1. Метод проектирования туннельного тюбинга

В настоящее время методы расчета внутренних усилий (расчет внутренней силы) для конструкций щитовых туннельных тюбингов в Китае включают метод эмпирической аналогии, метод предела сходимости, метод структурной нагрузки и метод стратиграфической структуры. Поскольку метод эмпирической аналогии не имеет теоретической базы и результатов расчета, он часто используется для оценки и дополнения других методов расчета. Тогда как принцип расчета метода предела сходимости все еще нуждается в дальнейшем исследовании и совершенствовании и часто используется для руководства строительством в сочетании с данными мониторинга строительной площадки. Метод стратиграфической структуры и метод структуры нагрузки являются теоретическими методами расчета с более строгой теоретической системой, а результаты расчета могут быть использованы для структурного проектирования и часто используются в качестве основы для проектирования. В соответствующих нормах проектирования в Китае для обычного проектирования рекомендуется метод структуры нагрузки, а в особых случаях для проверки можно использовать метод стратиграфической структуры.

В последние десятилетия метод расчета конструкции тюбинга для щитовых туннелей общего назначения среднего и малого диаметра (наружный диаметр туннеля D < 10 м) обычно основывается на нагрузке. Наиболее часто используемыми моделями являются однородная круговая модель, однородная круговая модель эквивалентной жесткости, упругая шарнирная круговая модель и двухкольцевая балка – модель пружины.

В модели однородного круга не учитывается снижение жесткости стыка тюбинговой части, и тюбинговая часть рассматривается как жесткое кольцо, а структурный анализ проводится напрямую. Грунтовые и водные нагрузки рассчитываются в соответствии с проницаемостью пласта как совместный расчет или расчет грунта и воды.

Вертикальное давление грунта определяется в зависимости от глубины туннеля и характера пласта с помощью полного давления вскрышного грунта или давления провисающего грунта, расчет давления провисающего грунта может быть рассчитан по формуле Тайшаджи, горизонтальное давление грунта рассчитывается в соответствии с вертикальным давлением грунта, умноженным на коэффициент бокового давления грунта. Вертикальная сила реакции основания определяется в соответствии с условием вертикального равновесия, а горизонтальная сила реакции основания рассматривается в диапазоне 45° выше и ниже центра конструкции в соответствии с законом распределения равнобедренного треугольника, и ее величина определяется в соответствии с горизонтальной деформацией, умноженной на коэффициент сопротивления основания. Эта модель возникла в Японии, поэтому ее называют общепринятой японской моделью.

Эквивалентная модель однородного кольца жесткости не учитывает напрямую существование стыков тюбинга при расчете и вводит коэффициент эффективности жесткости η и изгибающий момент ζ для отражения влияния кольцевых и продольных стыков тюбинга на внутреннюю силу, что является приблизительной упрощенной моделью конструкции щитовой обделки туннеля, где η применяется для отражения влияния уменьшения жесткости кольцевой обделки из-за наличия стыков тюбинга, а ζ – для отражения увеличения жесткости соседних колец обделки, поддерживаемых друг другом через межкольцевые стыки при ступенчатой сборке. Расчет нагрузки на грунт и воду и силы реакции основания в этой модели такой же, как и в однородной кольцевой модели. Для значений η и ζ в Японии после ряда экспериментов были даны рекомендуемые значения для различных диаметров и различных соединений, поэтому данная модель также называется доработанной японской моделью.

Модель упругошарнирного (многошарнирного) кольца моделирует соединение тюбинга как вращающуюся пружину с определенной жесткостью или непосредственно упрощенное сочленение без учета влияния каждого кольца между частями тюбинга. Само упругошарнирное (многошарнирное) кольцо является подвижной структурой, которая может быть стабилизирована только под действием реакции вмещающей породы, поэтому такая структура может быть использована только при относительно хорошем состоянии вмещающей породы. Кроме того, при использовании модели упругогошарнирного кольца точность расчета напрямую зависит от величины вращательной жесткости вращающейся пружины. Расчет нагрузки на грунт в этой модели в основном такой же, как и в однородной круговой модели, в то время как давление воды определяется в соответствии с высотой напора и затем направляется в центр формы трубчатого листа, а сопротивление грунта моделируется пружиной основания. Модель двухкольцевой балки-пружины использует вращающиеся пружины для моделирования соединений между каждым кольцом труб, а для туннелей, собранных со смещенными соединениями при моделировании кольцевых соединений используются радиальные и тангенциальные пружины сдвига. Моделирование стыковых соединений является более полным, также как и в модели упругого шарнирного кольца, точность результатов расчета модели двухкольцевой балки-пружины зависит от точности значения жесткости соединения. Расчет и моделирование нагрузок на грунт и воду и сопротивления пласта грунта в этой модели такие же, как и в модели упругого шарнирного кольца.

В последнее десятилетие появились щитовые туннели большого (D ≥ 10 м) и очень большого (D > 15 м) диаметра. Толщина обделки увеличивается с меньшей скоростью, чем диаметр туннеля, а количество продольных швов увеличивается из-за увеличения количества отрезков труб, жесткость на изгиб конструкции обделки щитовых туннелей большого и очень большого диаметра ниже, чем у щитовых туннелей малого диаметра. Для определения жесткости контура и продольных швов необходимо использовать расчетную модель на основе модельного испытания или испытания по следам, используя либо метод структуры нагрузки пружинной модели, либо стратиграфический метод.

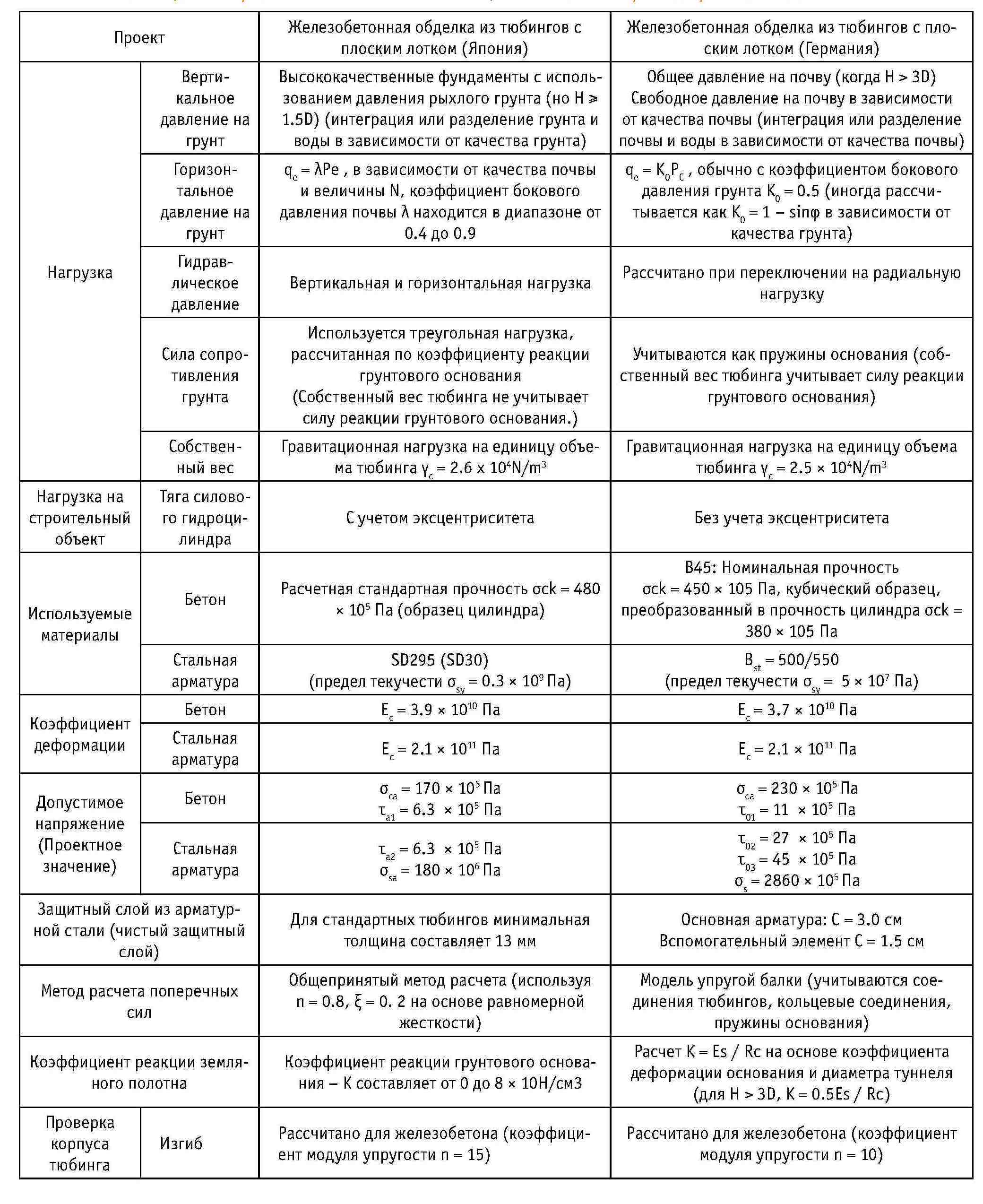
Основной процесс проектирования поперечного сечения тюбинга в Японии показан на рис. 4-1. В таблице 4-1 показаны методы проектирования, используемые в других странах, кроме Японии. В таблице 4-2 приведено сравнение японского и немецкого методов проектирования тюбинга, которые можно использовать в качестве справочной информации.

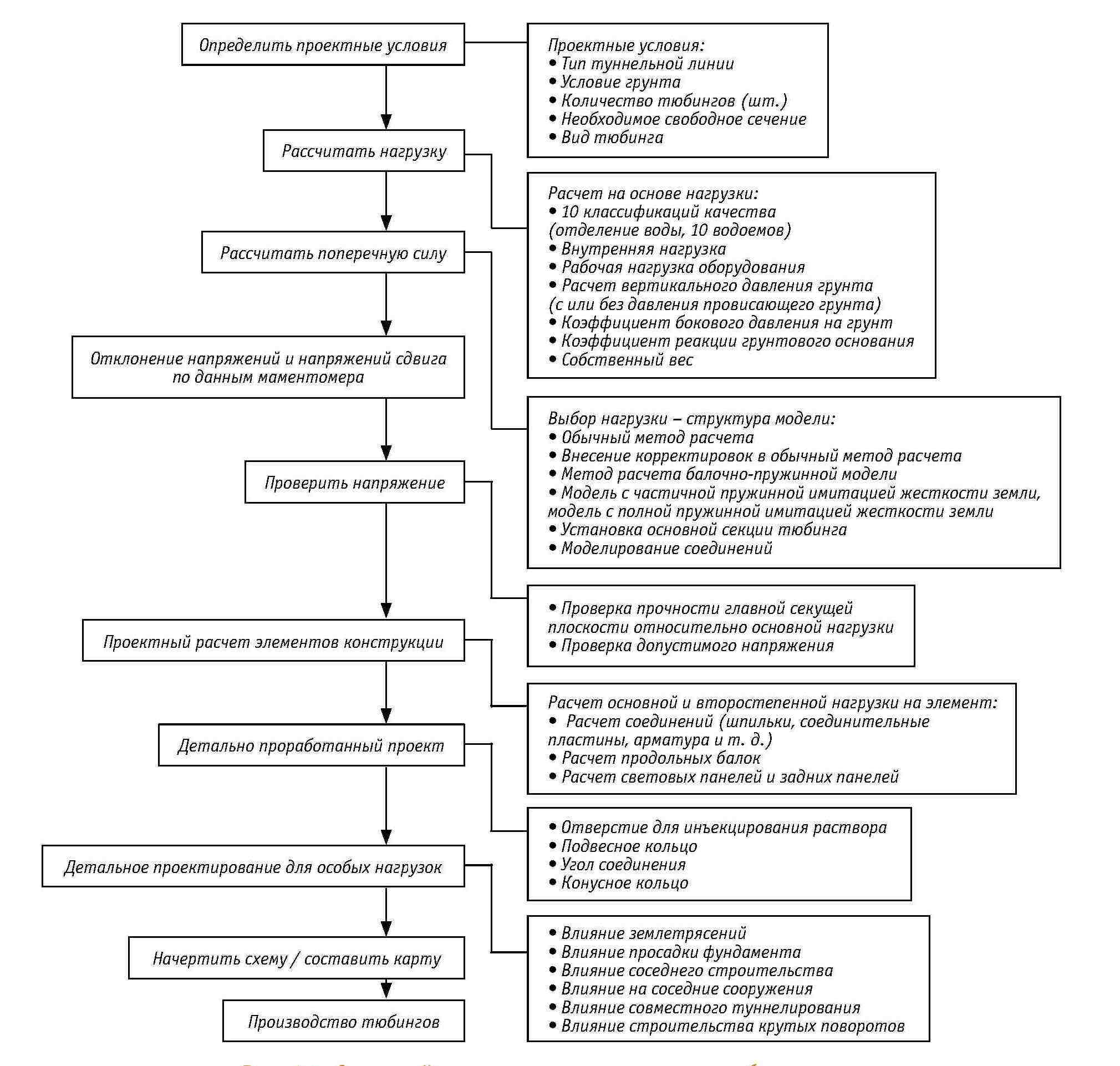
Рис. 4-1. Основной процесс проектирования тюбингов

Таблица 4-1. Методы проектирования щитовых туннелей в других странах (кроме Японии)

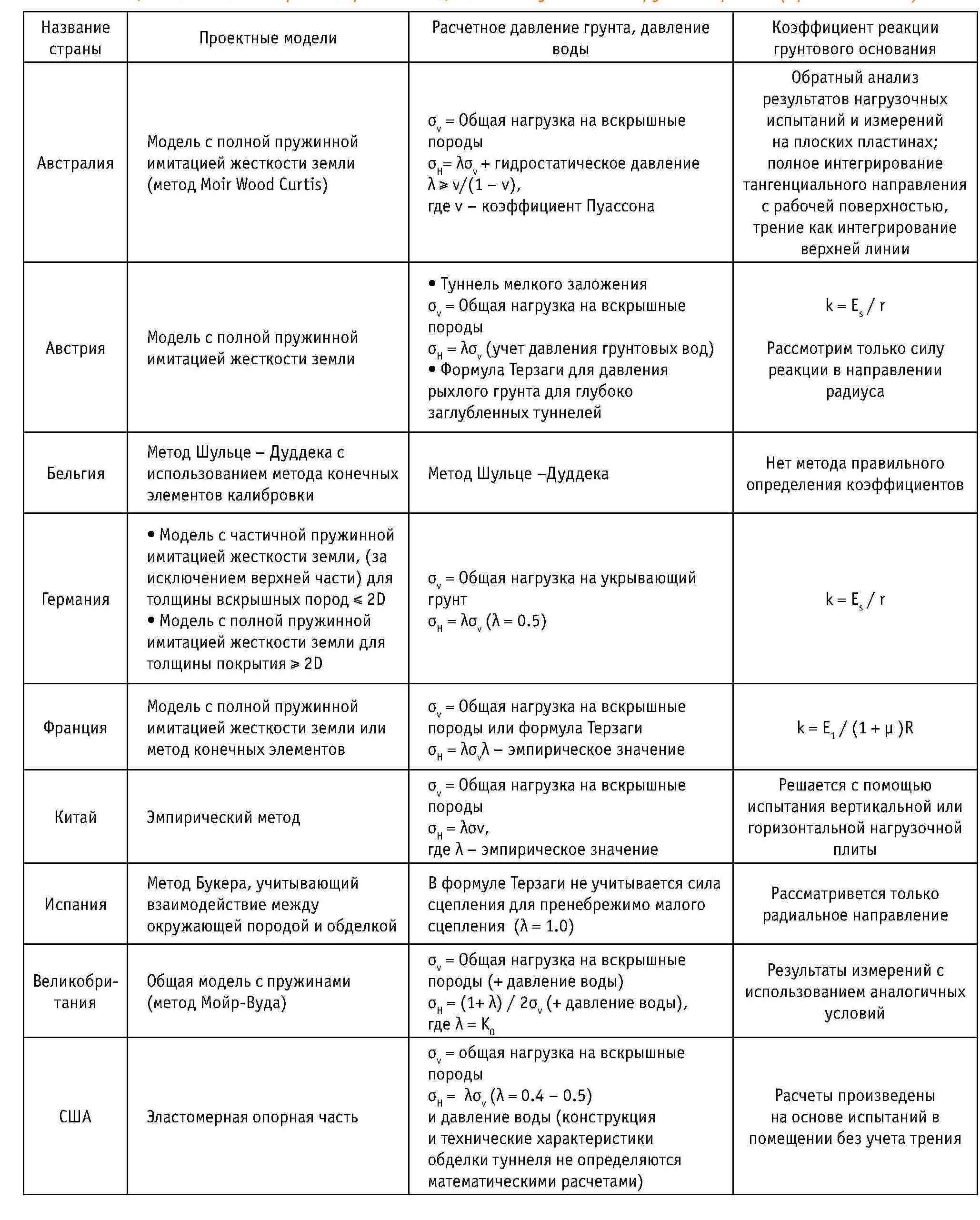
Таблица 4-2. Сравнение японского и немецкого методов проектирования тюбингов

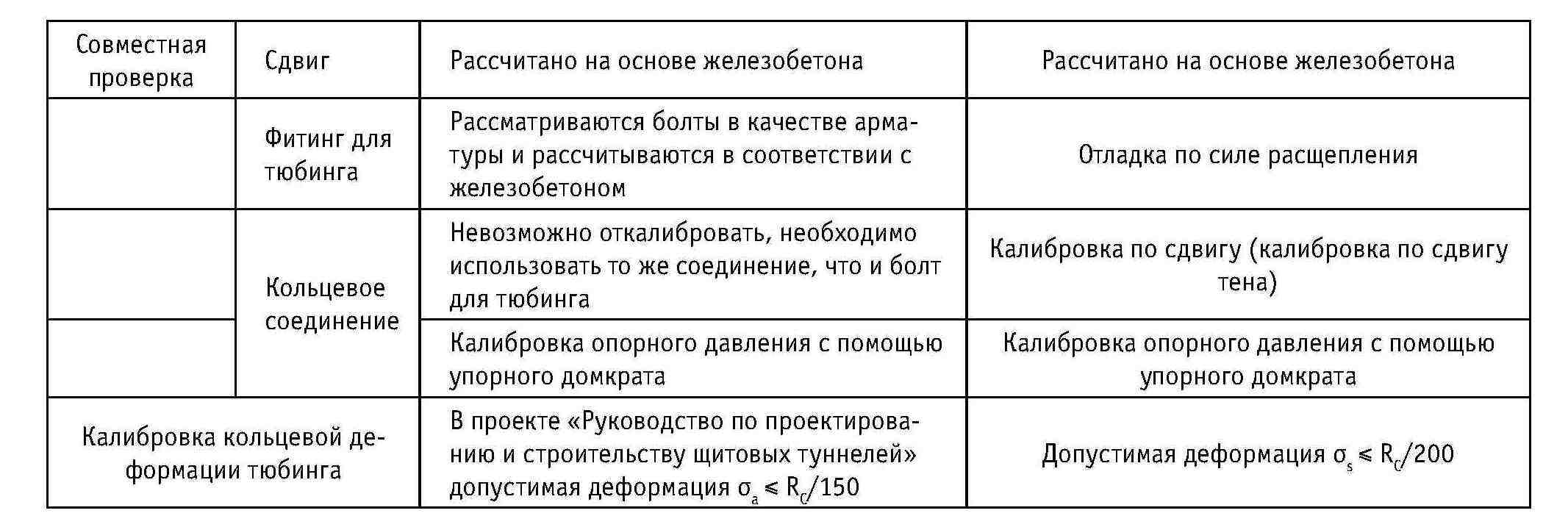
Несмотря на то, что условия заложения щитовых туннелей важны, существуют также различия в механических свойствах, обусловленные формой сечения и методом строительства, что, естественно, приводит к выбору различных методов проектирования тюбинга, где обделка должна быть спроектирована в соответствии с этими характеристиками. Исходя из прошлой практики, большинство туннелей имеют круглое сечение, поэтому в данном разделе основное внимание уделяется методам проектирования и опыту работы с круглыми сечениями.

4.1.2. Проектирование модели тюбинга

Более типичными упрощенными гипотетическими моделями тюбинга являются: кольцо тюбинга рассматривается как круглое кольцо с равномерной жесткостью на изгиб, кольцо тюбинга рассматривается как многошарнирное круглое кольцо и кольцо тюбинга рассматривается как круглое кольцо с вращающейся пружиной. Для первой из этих упрощенных гипотетических моделей существуют общие методы проектирования и модифицированные общие методы проектирования; для второй – аналитический метод для многошарнирных колец; для третьей – аналитический метод для моделей балка-пружина. В настоящее время в дополнение к вышеупомянутым трем типичным методам расчета конструкции тюбинга, метод проектирования с использованием пружин сдвига для оценки эффекта ступенчатого сращивания также вступил в практическую стадию.

1) Общие методы проектирования

Этот метод не учитывает снижение жесткости соединения тюбинга, а рассматривает его как круговое кольцо с равномерной жесткостью. При расчете предполагается, что грунт реагирует на деформацию кольца тюбинга и решается уравнение упругости. Общий метод проектирования – это текущий метод проектирования, обычно используемый в Японии. Для этого метода проектирования необходимы конкретные расчетные формулы.

2) Корректировка общего метода проектирования

Кольцо из тюбинга имеет стыки и, следовательно, пониженную жесткость. Если расчет основан на общем методе проектирования и учитывается влияние стыков, то процесс можно назвать модифицированным общим методом проектирования.

Даже если кольца расположены в шахматном порядке и сращиваются друг с другом из-за наличия швов в тюбинге общий расчетный метод коррекции предполагает равномерную изгибную жесткость ηEI (η ≤ 1) для сил кольцевого сечения (M, N, Q), которая меньше общей изгибной жесткости EI тюбинга, при этом параметр η называется эффективной скоростью изгибной жесткости.

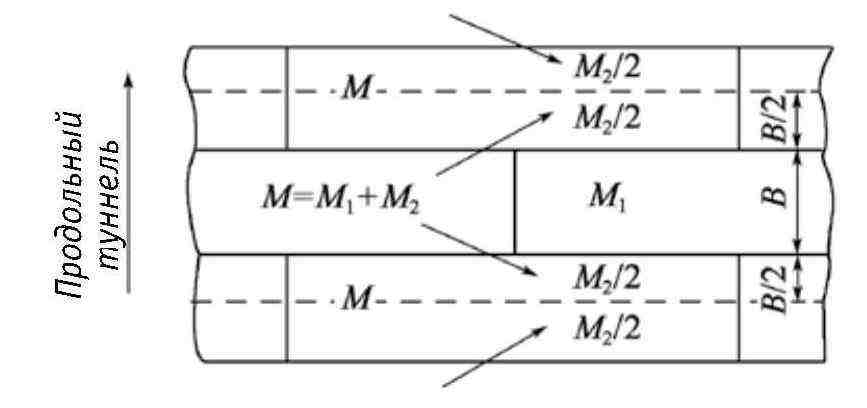
Рис. 4-2. Основная структура метода упругих шарнирных колец (продольный профиль туннеля)

Стыки тюбинга имеют некоторые характеристики сочленения, поэтому можно предположить, что не весь изгибающий момент передается стыками труб, а часть изгибающего момента передается на сцепленные соседние части тюбинга, как показано на рис. 4-2.

Этот метод целесообразно использовать для нахождения поперечных сил путем увеличения только изгибающего момента, который принимается равным (1 + ξ) M, в сочетании с осевой силой N для расчета. Параметр ξ представляет собой отношение изгибающего момента, передаваемого на соседний участок тюбинга, к расчетному изгибающему моменту и называется коэффициентом увеличения момента. Кроме того, в этом случае расчетный изгибающий момент и осевая сила соединения деталей тюбинга могут быть приняты равными (1 – ξ) М и (1 – ξ) N соответственно.

Параметры η и ξ изменяются в зависимости от типа тюбинга, конструктивной формы тюбингового соединения, способа сцепления колец и конструктивной формы; кроме того, на них особое влияние оказывают окружающие пласты. Теоретически метод расчета еще не установлен, но предполагается, что эти два параметра связаны друг с другом, то есть если значение η близко к 1, то значение ξ стремится к 0. При расчете поперечных сил с использованием модифицированного общего метода расчета, получение слишком малого значения η приведет к завышению сил реакции основания на пласты. В то же время, поперечные силы кольца тюбинга недооцениваются, поэтому значения этих параметров должны быть тщательно продуманы. Согласно существующей практике, значения параметров η и ξ определяются на основе результатов испытаний и опыта.

В связи с этим в японском стандарте на тюбинги для щитового строительства предусмотрено, что η обычно принимается равной 1, а ξ равно 0. Для сравнения, в некоторых проектах η = 0.8 и ξ = 0.3. В таблице 4-3 приведены примеры комбинации η и ξ.

Таблица 4-3. Значение η в сравнении со значением ξ

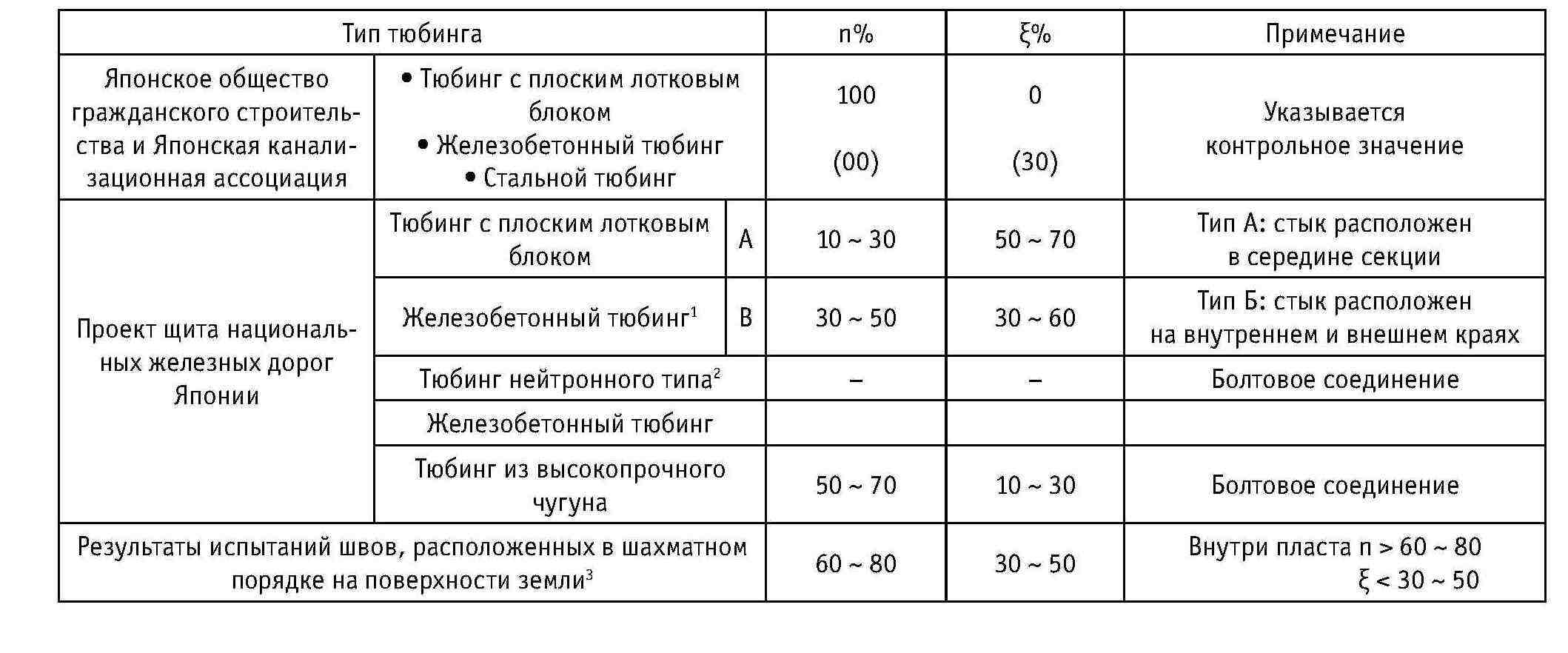
Примечание: 1) Как правило, ξ увеличивается по мере уменьшения η; 2) Несмотря на отсутствие примеров применения на национальных железных дорогах, прогнозируется, что значения η и ξ будут находиться между значениями для тюбинга с плоским лотковым блоком и тюбинга из высокопрочного чугуна; 3) Является результатом испытания под нагрузкой, опубликованным в «Стандартных деталях тюбинга для щитового строительства» (дополненное издание 1982 года).

3) Метод анализа многошарнирного кольца

Этот метод расчета представляет собой аналитический метод, который рассматривает шарнир как шарнирную конструкцию. Многошарнирное кольцо само по себе является неустойчивой конструкцией, но считается, что его можно превратить в устойчивую конструкцию, опираясь на реакции большой площади грунта вокруг туннеля. Предполагается, что существует равномерная радиальная сила реакции основания, распределенная вдоль кольца.

Этот метод расчета опирается на силы реакции пласта вокруг туннеля, поэтому при выборе подходящего основания необходимо соблюдать осторожность. Кроме того, во время сборки тюбинга и сразу после выпуска хвостового щита, когда силы реакции основания еще не действуют в полной мере, необходимо использовать вспомогательные средства, позволяющие кольцу тюбинга быть самонесущими, или сделать соединение тюбинга достаточно жестким, чтобы поддерживать само кольцо. Видно, что этот метод анализа обычно используется в ситуациях, когда грунтовые условия хорошие.

4) Метод упругого шарнирного кольца

Поскольку кольцо щитовых туннелей состоит из нескольких сборных частей, эти части можно соединять в стыки различной формы, при необходимости скрепляя их болтами. Собранные соединения не могут иметь такую же жесткость, как монолитная железобетонная конструкция. На самом деле, стыки отдельных частей имеют не жесткий шарнир и не полный шарнир, и величина изгибающего момента, который он может выдержать, связана с жесткостью шарнира K. Внутренние силы рассчитываются путем рассмотрения кольца тюбинга как кольца упругих шарниров на стыках труб. Жесткость соединения K обычно определяется эмпирически и экспериментально. Значения внутренних сил для каждой секции могут быть получены аналитически из основной конструкции, показанной на рис. 4-3.

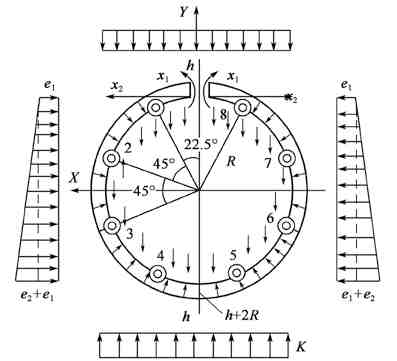
Рис. 4-3. Схематическая диаграмма аналитического метода решения значений внутренних сил для каждой секции

(5) Аналитический метод модели пружины-балки

Этот аналитический метод характеризуется моделированием кольца из тюбинга в виде балочной рамы (прямой или изогнутой балки), использованием вращающейся пружины и пружины сдвига для моделирования соединения тюбинга и конца кольца, соответственно, и использованием метода конечных элементов для анализа их упругих свойств для рамы и расчета поперечных сил. Этот аналитический метод является эффективным способом объяснения механизма несущей способности кольца из тюбинга.

При применении этого метода можно также рассчитать поперечные силы в случае кольцевых стыковых соединений тюбинга, двухкольцевых или трехкольцевых ступенчатых муфт и непосредственно найти поперечные силы между кольцами. Кроме того, когда постоянная величина пружины вращения соединения тюбинга равна 0, она такая же, как для многошарнирных колец; если она бесконечна, то такая же, как для равномерно жестких колец.

В последние годы многие ученые в Китае изучали проектирование тюбинга и придумали инновационные модели, чтобы компенсировать недостатки простых моделей.

(1) Трехмерная модель оболочки-пружины

Используется модель полной кольцевой футеровки, состоящая из полного кольца и двух полуколец, при этом среднее полное кольцо является целью исследования, а переднее и заднее полукольца – граничными условиями для среднего полного кольца, а также ступенчато соединенной силовой кольцевой структуры. Разработана модель конструкции под нагрузкой, а модель облицовки оболочки показана на рис. 4-4. Радиальное и тангенциальное сопротивление пласту моделируется пружинами. Учитывая, что сопротивление пласта грунта находится только под давлением, радиальная пружина напряжения на грунте автоматически отключается при ее вытягивании, а расположение блока пружин напряжения на земле показано на рис. 4-5.

Соединение тюбинга моделируется вращающейся пружиной, которая плотно размещена во всех узлах на торце соединения тюбинга. Пружина способна дополнить входной изгибающий момент, осевую силу и угол поворота кривой нелинейными параметрами. По сравнению с классической моделью пружинной балки, ее структурная форма и характер нагрузки в основном такие же, а основным прорывом является анализ распределения внутренних сил конструкции по амплитуде.

(2) Нагрузка – структурная модель оболочки-пружины – контактная модель

В модели «нагрузка – структурная модель оболочки-пружины – контактная модель» воздействие пласта на тюбинг достигается с помощью радиальных и тангенциальных фундаментных пружин. Эта модель учитывает эффект сжатия на стыках между тюбингом, перекрытие между тюбингом и болтовыми соединениями, радиальное и тангенциальное сопротивление пластов тюбинга, разницу между положительной и отрицательной изгибной жесткостью кольцевых соединений и угол вставки укупорочного блока. Он также обеспечивает условия для анализа продольной деформации, принимая во внимание механические механизмы растяжения болтов и сжатия водонепроницаемого материала в кольцевом пространстве во время продольной деформации. Этот метод может имитировать распространенный метод случайной сборки колец, как показано на рис. 4-6, и является более точным.

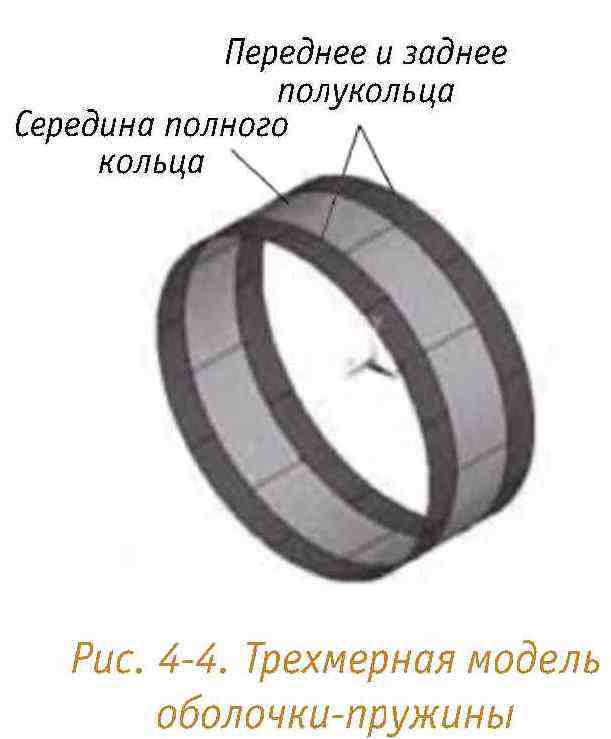
Рис. 4-4. Трехмерная модель оболочки-пружины

Рис. 4-5. Блок пружины напряжения грунта

Рис. 4-6. Разделение элементов тюбинга

(3) Стратиграфическая структурная модель с пружиной

Суть стратиграфической структурной модели заключается в учете влияния разгрузки напряжений в каверне после выемки грунта в исходном поле напряжений и совместной опоры породы периметра и структуры на стратиграфическое давление. Эквивалентные узловые силы вокруг отверстия извлекаются из рассчитанного поля напряжений собственного веса и дисконтируются с учетом снятия напряжений, затем прикладываются к узлам монолитных блоков вокруг отверстия и передаются на конструкцию туннеля через фундаментные блоки для достижения совместной опоры окружающей породы и конструкции. Процесс аналогичен процессу построения стратиграфической и структурной модели с использованием метода плоских конечных элементов. Разделение элементов конструкции и крепление болтов показано на рис. 4-7, 4-8.

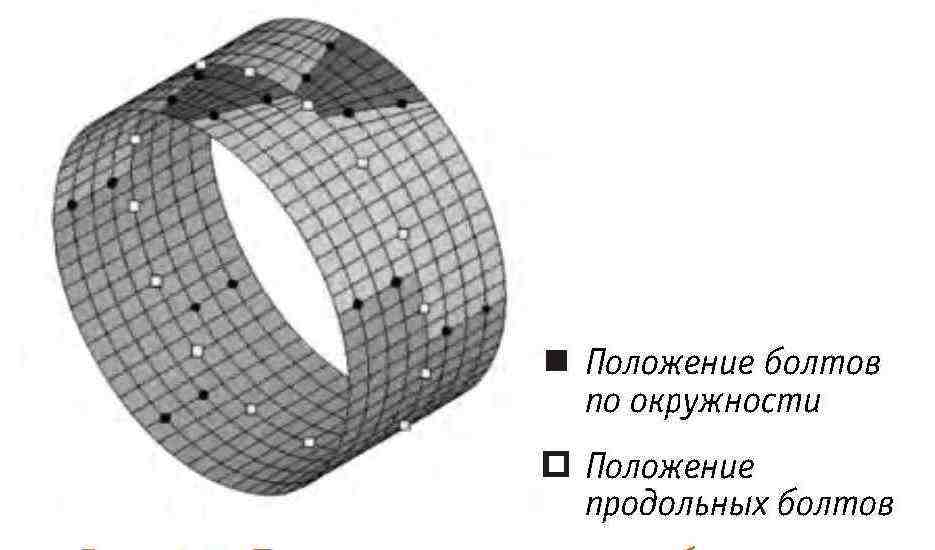
Рис. 4-7. Положение крепления болтов

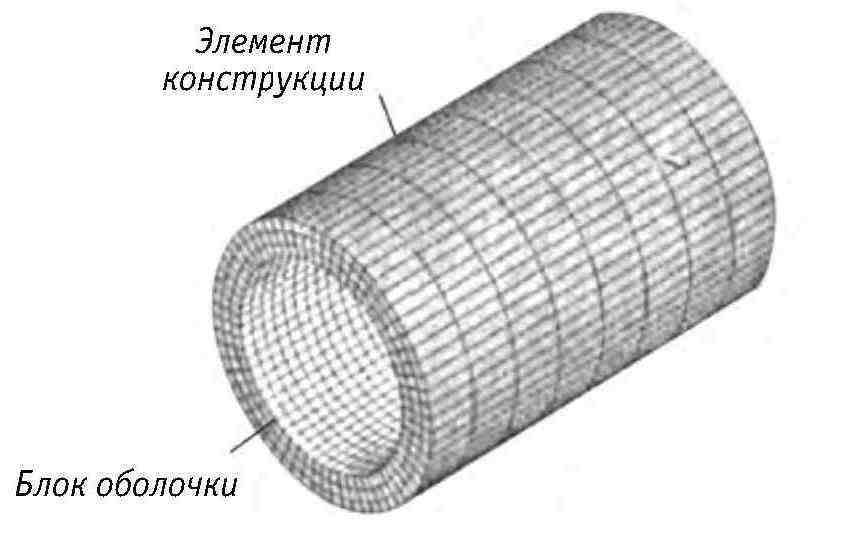
Рис. 4-8. Разделение элементов конструкции

(4) Модель оболочка-пружина с добавочным напряжением при продольной деформации Модель оболочка-пружина с добавочным напряжением при продольной деформации построена на основе конечных элементов, а для анализа дополнительных внутренних сил и деформаций в трехмерной структуре туннеля щита после возникновения продольных деформаций используется метод вынужденного перемещения. Данная модель была разработана с использованием блоков оболочки, блоков пружины сжатия, блоков пружины сдвига, блоков вращающейся пружины и блоков контакта, следуя идее модели оболочка-пружина с добавочным напряжением при продольной деформации для анализа поперечных внутренних сил щитовых туннелей.

4.1.3. Расчет нагрузки на тюбинг

1) Виды нагрузок и их комбинации

Разнообразие нагрузок, учитываемых при проектировании обделки, и многочисленные неопределенности в их значениях означают, что они должны устанавливаться в соответствии с различными условиями и методами проектирования, а также комбинироваться в зависимости от использования туннеля. Комбинация этих нагрузок варьируется в зависимости от назначения туннеля. Иногда даже необходимо комбинировать нагрузки в соответствии с наиболее неблагоприятными условиями, которые могут возникнуть на каждом этапе строительства и эксплуатации, например, выбирая комбинацию нагрузок, которая дает наибольшее воздействие нагрузки на конструкцию облицовки и наиболее неблагоприятные условия работы. В таблице 4-4 перечислены типы нагрузок, используемых при проектировании тюбингов.

Таблица 4-4. Виды нагрузок, используемые при проектировании тюбингов

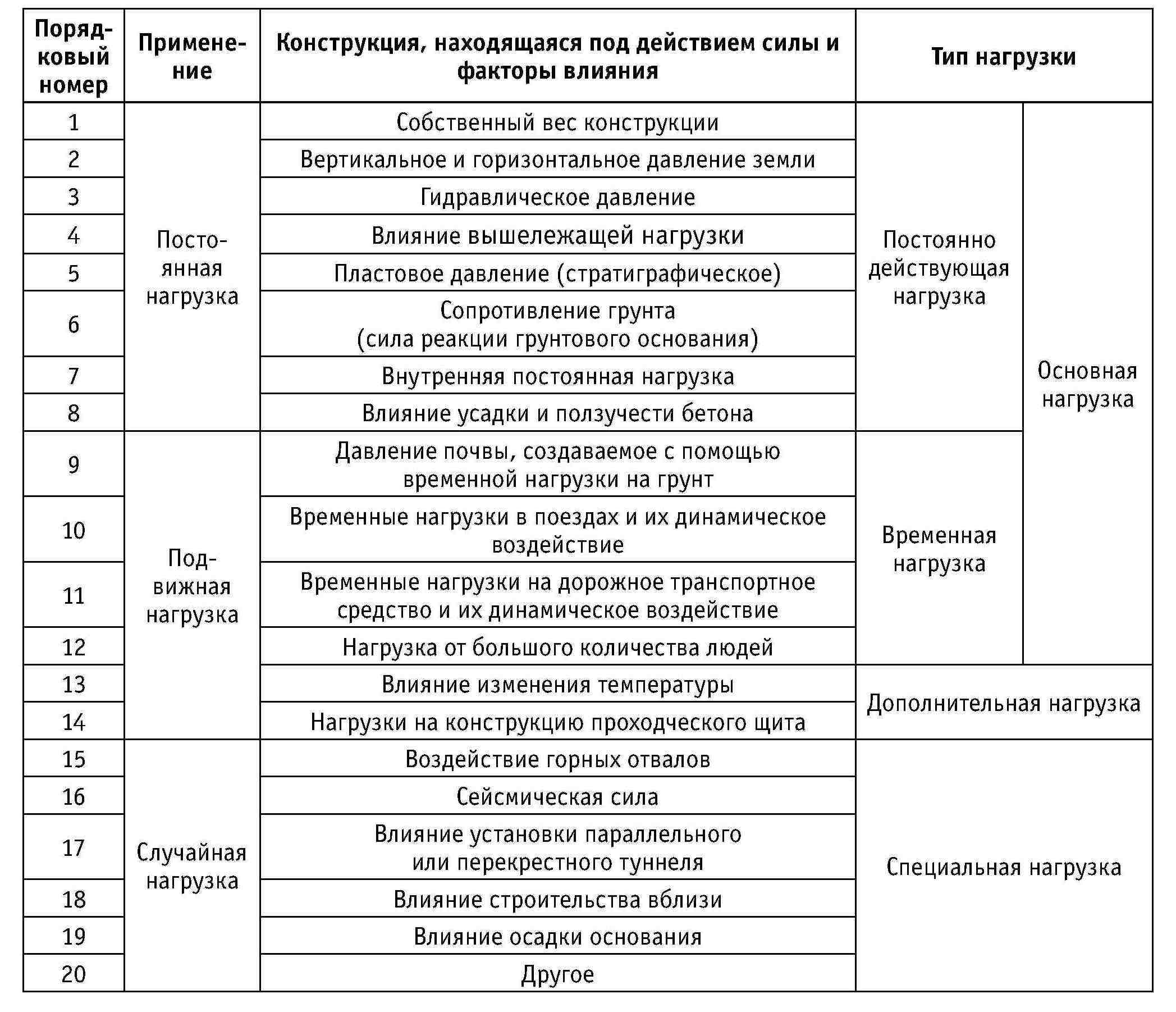
В приведенной выше таблице основные нагрузки – это основные нагрузки, которые обычно должны учитываться при проектировании тюбинга. Дополнительные нагрузки – это нагрузки, которые будут приложены во время строительства и после завершения строительства туннеля, это нагрузки, которые необходимо учитывать в зависимости от использования туннеля. Кроме того, специальные нагрузки – это нагрузки, которые должны быть специально учтены в зависимости от условий пласта, использования туннеля и т. д.

На рис. 4-9 показано распределение основных нагрузок в туннеле щита.

Рис. 4-9. Схематическая диаграмма распределения основных нагрузок в щитовом туннеле

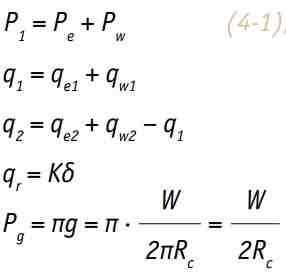
(4-1)

где: P e \ Pw – вертикальное давление в грунте и гидравлическое давление (кПа);

qe1 \ qe2 – горизонтальное давление в грунте (кПа);

qw1 \ qw2 – горизонтальное гидравлическое давление (кПа); qr – горизонтальное сопротивление грунта (кПа),

распределенное в диапазоне 45° выше и ниже горизонтального диаметра;

K – коэффициент горизонтального сопротивления грунта (кН/м3);

Δ – А горизонтальное смещение точки (м);

P g – сила реакции собственного веса конструкции (кПа);

W – вес на единицу длины кольца тюбинга (кН).

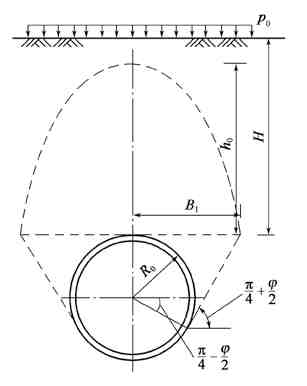
Рис. 4-10. Схема расчетной модели для давления на рыхлый грунт

2) Давление на грунт Давление на грунт, используемое для проектного расчета тюбинга, состоит из вертикального давления в грунте и горизонтального давления в грунте, значения которых не зависят от деформации туннеля. Кроме того, давление грунта на дно туннеля можно рассматривать как обратное давление грунта и трактовать как силу реакции основания. Существует два способа расчета давления грунта, один из которых заключается в том, чтобы рассматривать давление воды как часть давления грунта. Другой способ заключается в расчете давления воды отдельно от давления грунта. Первый обычно используется для вязких грунтов, а второй – для песчаных почв. Для промежуточных почв нет четких критериев, но коэффициент проницаемости от 10-4 ~ 10-3 см/с может быть использован в качестве отсекающего значения. В случае давления почвы и давления воды используется влажная мощность выше уровня грунтовых вод и насыщенная мощность ниже уровня грунтовых вод; в случае давления воды и давления почвы используется влажная мощность выше уровня грунтовых вод и плавающая мощность ниже уровня грунтовых вод.