
Полная версия
Нейросети. Обработка естественного языка
– Проблема затухания градиентов:
Важно отметить, что у классических RNN есть проблема затухания градиентов, которая может привести к утере информации о более давних элементах последовательности. Это ограничение привело к разработке более сложных архитектур RNN, таких как LSTM и GRU, которые способны эффективнее работать с долгосрочными зависимостями в данных.
Скрытое состояние в RNN играет важную роль в обработке последовательных данных и позволяет сетям учитывать контекст и зависимости между элементами в последовательности. Различные модификации RNN, такие как LSTM и GRU, были разработаны для устранения ограничений и улучшения способности моделей к обработке более долгих и сложных последовательностей.
Для наглядного представления скрытого состояния в рекуррентных нейронных сетях (RNN), давайте представим ситуацию, связанную с обработкой текстовых данных, чтобы понять, как это работает.
Представьте, что у нас есть следующее предложение: "Сегодняшняя погода очень хорошая." Мы хотим использовать RNN для анализа тональности этого предложения и определения, положительное оно или отрицательное.
1. Инициализация скрытого состояния:
На первом шаге обработки этого предложения скрытое состояние инициализируется некоторым начальным значением, например, нулевым вектором. Это начальное состояние несет в себе информацию о предыдущих шагах, но на этом этапе оно пустое.
2. Обработка слов поочередно:
Теперь мы начинаем обрабатывать слова в предложении поочередно, шаг за шагом. Для каждого слова RNN обновляет свое скрытое состояние, учитывая информацию о предыдущих словах и текущем слове. На этом этапе RNN может учитывать, что "Сегодняшняя" и "погода" идут перед "очень" и "хорошая", и что они могут влиять на общий смысл предложения.
3. Агрегация информации:
После обработки всех слов в предложении скрытое состояние будет содержать информацию, учитывающую контекст всего предложения. Это состояние может отражать, что весь контекст в данном предложении указывает на положительную тональность.
4. Выдача результата:
Наконец, RNN может использовать это скрытое состояние для определения тональности предложения, и, например, классифицировать его как "положительное".
Исходное состояние скрытого состояния (шаг 1) и его изменение по мере обработки каждого слова (шаги 2 и 3) – это ключевые элементы работы RNN в обработке текстовых данных. Это позволяет модели учитывать зависимости между словами и контекст, что делает RNN мощными инструментами в NLP.
Затем, чтобы понять, как работают более продвинутые архитектуры, такие как LSTM и GRU, можно представить их как улучшенные версии RNN с более сложными механизмами обновления скрытого состояния, которые позволяют им эффективнее учитывать долгосрочные зависимости в данных.
Для реализации рекуррентной нейронной сети (RNN) в коде на Python с использованием библиотеки глубокого обучения TensorFlow, можно следовать следующему шаблону. В данном примере будет использован простой пример классификации текста с использованием RNN:
```python
import tensorflow as tf
from tensorflow.keras.layers import Embedding, SimpleRNN, Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
# Пример текстовых данных для обучения
texts = ["Сегодняшняя погода очень хорошая.", "Дождь идет весь день.", "Ветер сильный, но солнце светит."]
labels = [1, 0, 1] # 1 – положительное, 0 – отрицательное
# Создание токенизатора и преобразование текста в последовательности чисел
tokenizer = Tokenizer()
tokenizer.fit_on_texts(texts)
sequences = tokenizer.texts_to_sequences(texts)
# Паддинг последовательностей для обеспечения одинаковой длины
max_sequence_length = max([len(seq) for seq in sequences])
sequences = pad_sequences(sequences, maxlen=max_sequence_length)
# Создание модели RNN
model = Sequential()
model.add(Embedding(input_dim=len(tokenizer.word_index) + 1, output_dim=64, input_length=max_sequence_length))
model.add(SimpleRNN(32))
model.add(Dense(1, activation='sigmoid')) # Бинарная классификация
# Компиляция модели
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# Обучение модели
model.fit(sequences, labels, epochs=10, batch_size=1)
# Пример тестовых данных для предсказания
test_texts = ["Завтра будет солнечно.", "Дождь мне не нравится."]
test_sequences = tokenizer.texts_to_sequences(test_texts)
test_sequences = pad_sequences(test_sequences, maxlen=max_sequence_length)
# Предсказание классов
predictions = model.predict(test_sequences)
for i, text in enumerate(test_texts):
sentiment = "положительное" if predictions[i] > 0.5 else "отрицательное"
print(f"Текст: {text}, Прогноз тональности: {sentiment}")
```
Этот код демонстрирует базовую реализацию RNN для задачи анализа тональности текста. Важно отметить, что в реальных приложениях могут использоваться более сложные архитектуры и данные.
2. Обратные связи (Feedback Loops):
Обратные связи (Feedback Loops) представляют собой ключевой механизм в рекуррентных нейронных сетях (RNN) и других последовательных моделях машинного обучения. Эти обратные связи обеспечивают возможность информации циркулировать между различными моментами времени в последовательности данных, позволяя предыдущим шагам влиять на текущие вычисления. Давайте более подробно разберемся, как это работает:
1. Последовательные данные:
Обратные связи особенно полезны при работе с последовательными данными, такими как тексты, временные ряды или аудиосигналы, где значения зависят от предыдущих значений.
2. Скрытое состояние:
Основной механизм обратной связи в RNN заключается в использовании скрытого состояния (Hidden State). На каждом временном шаге RNN обновляет свое скрытое состояние с учетом текущего входа и предыдущего состояния.
3. Информация о контексте:
Скрытое состояние сохраняет информацию о предыдущих элементах последовательности. Это позволяет модели учитывать контекст и зависимости между данными в разных частях последовательности.
4. Пример работы:
Давайте представим следующую последовательность слов: "Я ел бутерброд. Затем я выпил чашку кофе." В контексте обратных связей, RNN начнет с анализа слова "Я", и его скрытое состояние будет содержать информацию о нем. Когда сеть перейдет к слову "ел", скрытое состояние будет учитывать и слово "Я", и слово "ел". Затем, когда сеть дойдет до "бутерброд", скрытое состояние будет содержать информацию о всех трех предыдущих словах. Это позволяет модели понимать, что "ел" – это глагол, относящийся к действию, начатому в предыдущем предложении.
5. Затухание и взрыв градиентов:
Важно отметить, что обратные связи также могут быть источником проблем, таких как затухание и взрыв градиентов. Если градиенты становятся слишком большими (взрыв градиентов) или слишком маленькими (затухание градиентов), обучение RNN может стать затруднительным. Для решения этой проблемы были разработаны модификации RNN, такие как LSTM и GRU, которые эффективнее управляют обратными связями и градиентами.
Обратные связи и скрытое состояние позволяют RNN учитывать контекст и зависимости в последовательных данных, что делает их мощными инструментами в обработке текста, аудио и других последовательных данных.
Для наглядности работы обратных связей (Feedback Loops) в рекуррентных нейронных сетях (RNN), давайте представим упрощенную аналогию. Допустим, у нас есть "ум" с карандашом, который пытается решить математическую задачу, но его способность решать задачи основывается на информации, которую он имеет о предыдущих задачах. Это можно представить следующим образом:
Первая задача: Ум начинает решать математическую задачу: 2 + 2. Он записывает результат, равный 4, на листе бумаги.
Обратная связь: Теперь, когда ум попытается решить следующую задачу, он видит результат предыдущей задачи на своей записи. Это дает ему контекст и информацию для решения следующей задачи.
Вторая задача: 3 + 3. Ум видит, что в предыдущей задаче было 2 + 2 = 4. Это важная информация, которая позволяет ему сделать вывод о том, как правильно решить новую задачу. Он записывает результат 6 на бумаге.
Продолжение обратных связей: Процесс продолжается. Каждая задача дополняет записи ума, и он использует информацию из предыдущих задач для решения новых задач.
Таким образом, информация из предыдущих задач (или моментов времени) влияет на текущие вычисления и помогает уму (или нейронной сети) учитывать контекст и зависимости между задачами (или данными) в последовательности. Это аналогия к тому, как обратные связи в RNN позволяют модели учитывать контекст и зависимости в последовательных данных, обновляя скрытое состояние на каждом временном шаге.
3. Параметры, обучаемые сетью:
Параметры, обучаемые сетью, играют критическую роль в работе рекуррентных нейронных сетей (RNN). Эти параметры являются настраиваемыми переменными, которые сеть использует для адаптации к конкретной задаче путем оптимизации их с использованием методов, таких как градиентный спуск. Вот подробное объяснение этого концепта:
1. Параметры сети:
– Веса (Weights): Веса связей между нейронами внутри RNN. Эти веса определяют, как информация передается от одного нейрона к другому и как она обновляется на каждом временном шаге.
– Смещения (Biases): Смещения добавляются к взвешенной сумме входов, перед применением активационной функции, и могут управлять смещением активации нейронов.
2. Инициализация параметров: Параметры RNN обычно инициализируются случайными значениями перед началом обучения. Эти начальные значения могут быть заданы случайным образом или с использованием различных методов инициализации весов.
3. Обучение сети: Во время обучения RNN параметры модели настраиваются для минимизации функции потерь (loss function) на тренировочных данных. Это происходит с использованием методов оптимизации, таких как градиентный спуск (gradient descent).
4. Градиентный спуск – это оптимизационный метод, который используется для обновления параметров сети на каждом этапе обучения. Он вычисляет градиент (производные) функции потерь по параметрам сети и обновляет параметры в направлении, которое минимизирует функцию потерь.
5. Итерации обучения: Обучение RNN происходит итеративно на множестве тренировочных данных. На каждой итерации параметры обновляются таким образом, чтобы уменьшить ошибку модели на тренировочных данных.
6. Результат обучения: После завершения обучения параметры RNN настроены таким образом, чтобы модель могла делать предсказания на новых данных, которые она ранее не видела.
7. Тонкая настройка: Важно отметить, что оптимизация параметров RNN – это искусство, и существует много методов для тонкой настройки параметров и параметров оптимизации, чтобы достичь лучшей производительности на конкретной задаче.
Параметры, обучаемые сетью, позволяют RNN адаптироваться к различным задачам и данным, делая их мощным инструментом для разнообразных задач, связанных с последовательными данными, включая обработку текста, анализ временных рядов и многое другое.
Давайте рассмотрим пример использования обучаемых параметров в нейронной сети на языке Python с использованием библиотеки TensorFlow. В этом примере мы создадим простую RNN для задачи прогнозирования временных рядов.
```python
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN, Dense
# Генерируем пример временного ряда
np.random.seed(0)
n_steps = 100
time = np.linspace(0, 10, n_steps)
series = 0.1 * time + np.sin(time)
# Подготавливаем данные для обучения RNN
n_steps = 30 # количество временных шагов в одной последовательности
n_samples = len(series) – n_steps
X = [series[i:i+n_steps] for i in range(n_samples)]
y = series[n_steps:]
X = np.array(X).reshape(-1, n_steps, 1)
y = np.array(y)
# Создаем модель RNN
model = Sequential()
model.add(SimpleRNN(10, activation="relu", input_shape=[n_steps, 1]))
model.add(Dense(1))
# Компилируем модель
model.compile(optimizer="adam", loss="mse")
# Обучаем модель
model.fit(X, y, epochs=10)
# Делаем прогноз на будущее
future_steps = 10
future_x = X[-1, :, :]
future_predictions = []
for _ in range(future_steps):
future_pred = model.predict(future_x.reshape(1, n_steps, 1))
future_predictions.append(future_pred[0, 0])
future_x = np.roll(future_x, shift=-1)
future_x[-1] = future_pred[0, 0]
# Выводим результаты
import matplotlib.pyplot as plt
plt.plot(np.arange(n_steps), X[-1, :, 0], label="Исходные данные")
plt.plot(np.arange(n_steps, n_steps+future_steps), future_predictions, label="Прогноз")
plt.xlabel("Временной шаг")
plt.ylabel("Значение")
plt.legend()
plt.show()
```
В этом примере:
– Мы создаем простую RNN с одним слоем, который прогнозирует следующее значение временного ряда на основе предыдущих значений.
– Обучаем модель с использованием оптимизатора "adam" и функции потерь "mse" (Mean Squared Error).
– Затем делаем прогнозы на несколько временных шагов вперед, обновляя входные данные с учетом предсказанных значений.
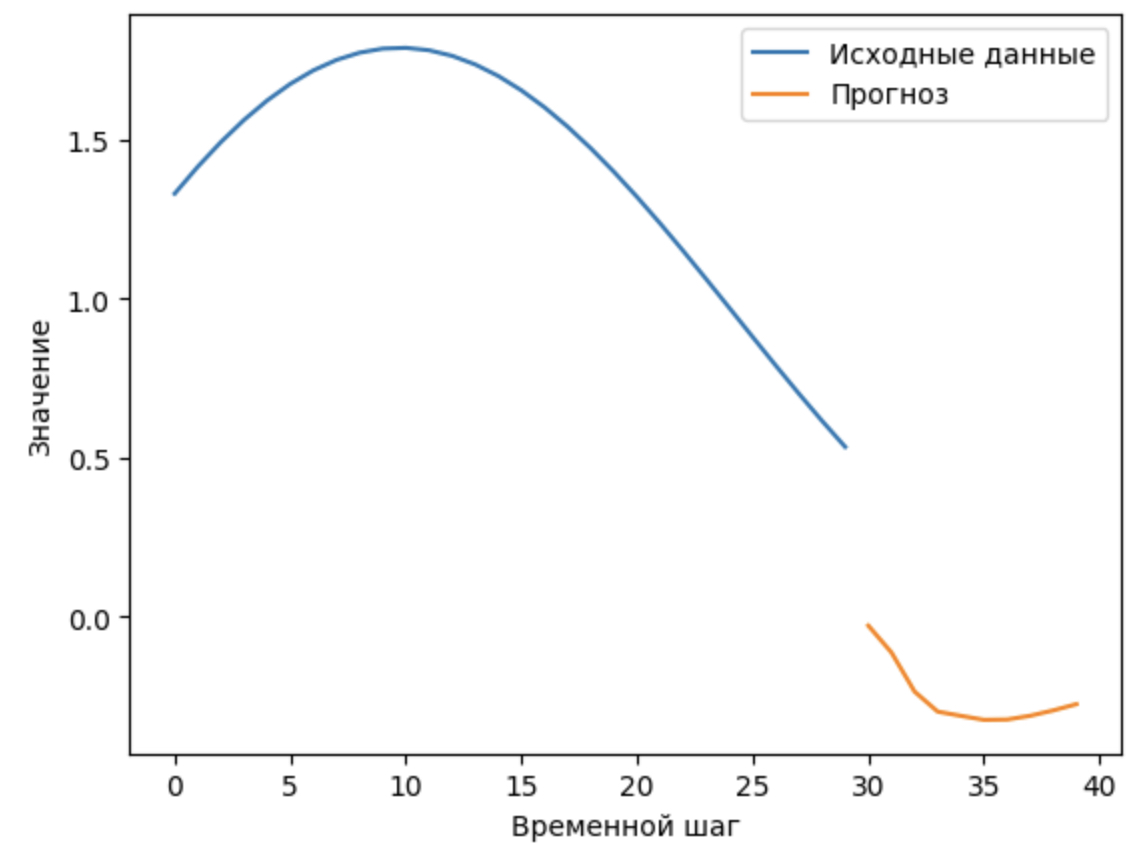
На результате кода, который вы предоставили, мы видим следующее:
1. Исходные данные (синяя линия): Это начальная часть временного ряда, который был сгенерирован. В данном случае, это линейная функция (0.1 * time) с добавленными синусоидальными колебаниями (np.sin(time)).
2. Прогноз (оранжевая линия): Это результаты прогноза, сделанные моделью RNN на будущее. Модель обучается на исходных данных и затем пытается предсказать значения временного ряда на заданное количество временных шагов вперед (future_steps).
Из этой визуализации видно, как модель RNN пытается аппроксимировать исходный временной ряд и делает прогнозы на основе предыдущих значений. Оранжевая линия отображает прогнозируемую часть временного ряда на будущее.
Завершив обучение и сделав прогнозы, вы можете визуально оценить, насколько хорошо модель справилась с задачей прогнозирования временного ряда.
В этом примере обучаемые параметры модели – это веса и смещения в слое RNN и в слое Dense. Модель настраивает эти параметры в процессе обучения, чтобы минимизировать ошибку прогноза временного ряда.
Обучаемые параметры позволяют модели адаптироваться к данным и находить закономерности, что делает их мощным инструментом для разнообразных задач машинного обучения.
Однако RNN имеют несколько ограничений, из которых наиболее значимой является проблема затухания градиентов (vanishing gradients). Эта проблема заключается в том, что при обучении RNN градиенты (производные функции потерь по параметрам сети) могут становиться очень маленькими, особенно на длинных последовательностях. Это затрудняет обучение, поскольку сеть может "забывать" информацию о давно прошедших событиях в последовательности.
Для решения проблемы затухания градиентов были разработаны более продвинутые архитектуры RNN:
Long Short-Term Memory (LSTM):
Long Short-Term Memory (LSTM) – это одна из наиболее популярных архитектур в области рекуррентных нейронных сетей (RNN). Она разработана для работы с последовательными данными и способна эффективно учитывать долгосрочные зависимости в данных. Давайте подробнее разберем, как работает LSTM:
Специальные ячейки LSTM: Основная особенность LSTM заключается в использовании специальных ячеек памяти, которые позволяют сохранять и извлекать информацию из прошлых состояний. Эти ячейки состоят из нескольких внутренних гейтов (гейт – это устройство, которое решает, какая информация должна быть сохранена и какая должна быть проигнорирована).
Забывающий гейт (Forget Gate): Этот гейт определяет, какая информация из прошлых состояний следует забыть или удалить из памяти ячейки. Он работает с текущим входом и предыдущим состоянием и выдает значение от 0 до 1 для каждой информации, которая указывает, следует ли ее забыть или сохранить.
Входной гейт (Input Gate): Этот гейт определяет, какая информация из текущего входа должна быть добавлена в память ячейки. Он также работает с текущим входом и предыдущим состоянием, и вычисляет, какие значения следует обновить.
Обновление памяти (Cell State Update): На этом этапе обновляется состояние памяти ячейки на основе результатов забывающего гейта и входного гейта. Это новое состояние памяти будет использоваться на следующем временном шаге.
Выходной гейт (Output Gate): Этот гейт определяет, какую информацию из текущего состояния памяти следует использовать на выходе. Он учитывает текущий вход и предыдущее состояние, чтобы определить, какую информацию передать на выход.
Долгосрочные зависимости: Благодаря специальным ячейкам и гейтам, LSTM способна учитывать долгосрочные зависимости в данных. Она может эффективно хранить информацию на протяжении многих временных шагов и извлекать ее, когда это необходимо.
Применение LSTM: LSTM широко используется в задачах, связанных с последовательными данными, таких как обработка текста, анализ временных рядов, машинный перевод, генерация текста и многие другие. Ее способность учитывать долгосрочные зависимости делает ее мощным инструментом для анализа и моделирования последовательных данных.
Лучший способ понять, как работает Long Short-Term Memory (LSTM), – это применить его на практике в рамках конкретной задачи. Давайте рассмотрим пример применения LSTM для анализа временных рядов в Python с использованием библиотеки TensorFlow и библиотеки pandas:
```python
import numpy as np
import tensorflow as tf
import pandas as pd
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense
# Генерируем пример временного ряда (синусоида)
timesteps = np.linspace(0, 100, 400)
series = np.sin(timesteps)
# Создаем датасет для обучения сети
df = pd.DataFrame({'timesteps': timesteps, 'series': series})
window_size = 10 # Размер окна для создания последовательных образцов
batch_size = 32 # Размер пакета
# Функция для создания последовательных образцов из временного ряда
def create_sequences(series, window_size, batch_size):
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(1000).map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return dataset
train_dataset = create_sequences(series, window_size, batch_size)
# Создаем модель LSTM
model = Sequential([
LSTM(50, return_sequences=True, input_shape=[None, 1]),
LSTM(50),
Dense(1)
])
# Компилируем модель
model.compile(loss='mse', optimizer='adam')
# Обучаем модель
model.fit(train_dataset, epochs=10)
# Делаем прогноз на будущее
future_timesteps = np.arange(100, 140, 1)
future_series = []
for i in range(len(future_timesteps) – window_size):
window = series[i:i + window_size]
prediction = model.predict(window[np.newaxis])
future_series.append(prediction[0, 0])
# Визуализируем результаты
plt.figure(figsize=(10, 6))
plt.plot(timesteps, series, label="Исходный ряд", linewidth=2)
plt.plot(future_timesteps[:-window_size], future_series, label="Прогноз", linewidth=2)
plt.xlabel("Время")
plt.ylabel("Значение")
plt.legend()
plt.show()
```
Этот пример демонстрирует, как можно использовать LSTM для прогнозирования временных рядов. Мы создаем модель LSTM, обучаем ее на исходном временном ряде и делаем прогнозы на будущее. Визуализация показывает, как модель способна улавливать долгосрочные зависимости в данных и строить прогнозы.
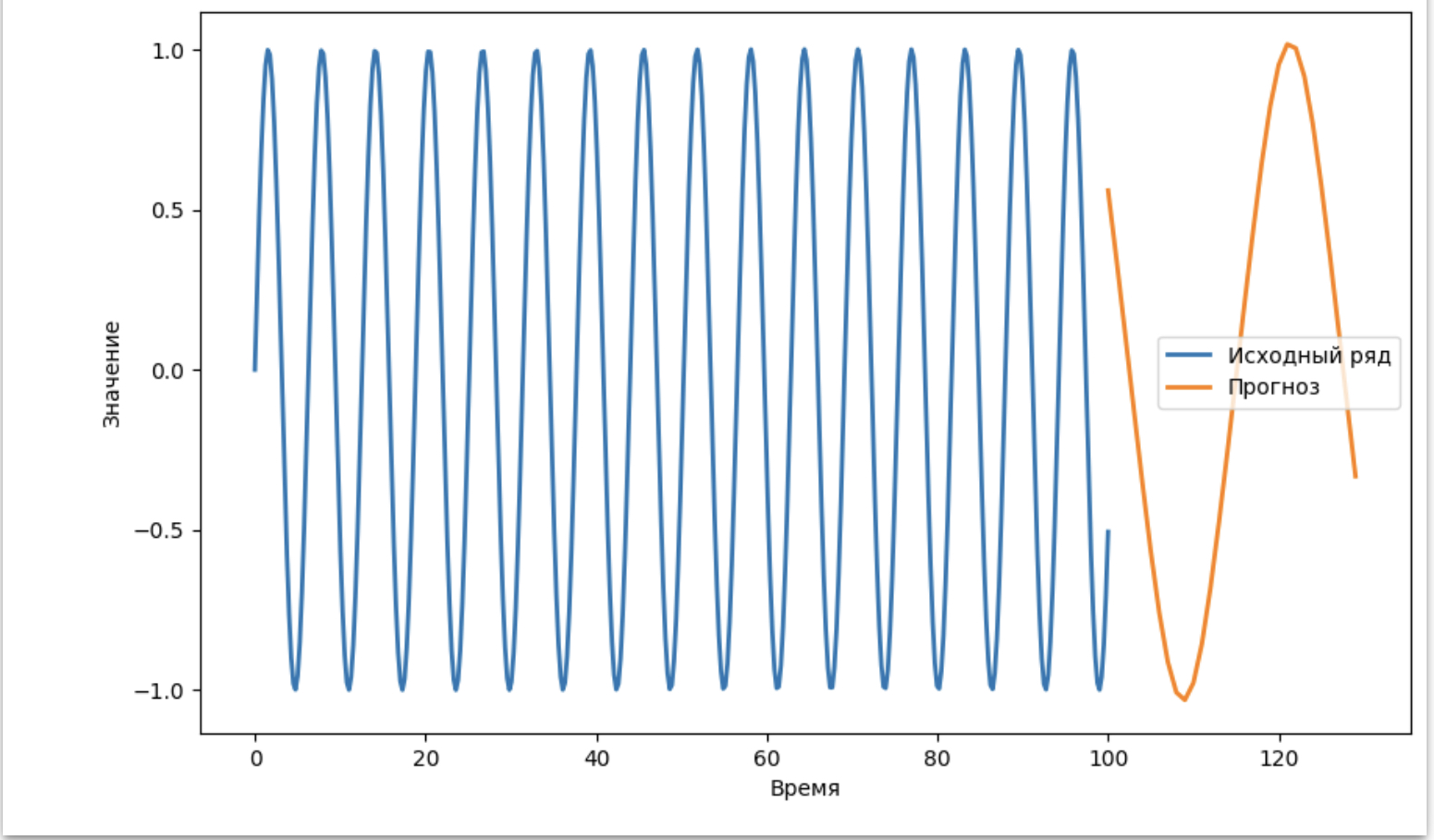
На результате данного примера мы видим следующее:
1. Исходный временной ряд (синяя линия): Это синусоидальная волна, которая была сгенерирована как пример временного ряда.
2. Прогноз модели (оранжевая линия): Это результаты прогноза, сделанные моделью LSTM на будущее. Модель пытается предсказать значения временного ряда на основе предыдущих значений. Оранжевая линия отображает прогнозируемую часть временного ряда.
Из этой визуализации видно, что модель LSTM смогла захватить основные характеристики синусоидального временного ряда и предсказать его продолжение на будущее. Этот пример демонстрирует, как LSTM может использоваться для анализа и прогнозирования временных рядов, а также как она учитывает долгосрочные зависимости в данных.
2. Gated Recurrent Unit (GRU):
GRU (Gated Recurrent Unit) – это архитектура рекуррентных нейронных сетей (RNN), которая, как вы сказали, является более легкой и вычислительно эффективной по сравнению с LSTM (Long Short-Term Memory). GRU была разработана для решения проблемы затухания градиентов, которая является одной из основных проблем при обучении RNN.
Вот основные характеристики GRU:
1. Воротные механизмы (Gating Mechanisms): GRU также использует воротные механизмы, как LSTM, но в упрощенной форме. У нее есть два ворота – ворот восстановления (Reset Gate) и ворот обновления (Update Gate).
2. Ворот восстановления (Reset Gate): Этот ворот решает, какую информацию из предыдущего состояния следует забыть. Если сброс (reset) равен 1, то модель забывает всю информацию. Если сброс равен 0, то вся информация сохраняется.
3. Ворот обновления (Update Gate): Этот ворот определяет, какая информация из нового входа следует использовать. Если значение ворота обновления близко к 1, то новая информация будет использоваться практически полностью. Если близко к 0, то новая информация будет игнорироваться.
4. Скрытое состояние (Hidden State): GRU также имеет скрытое состояние, которое передается от одного временного шага к другому. Однако, в отличие от LSTM, GRU не имеет ячейки памяти, что делает ее более легкой.
5. Затухание градиентов: GRU спроектирована так, чтобы бороться с проблемой затухания градиентов, которая может возникнуть при обучении глубоких RNN. Благодаря воротным механизмам, GRU может регулировать поток информации и избегать слишком быстрого затухания или взрывного увеличения градиентов.
6. Применение: GRU часто применяется в задачах анализа текста, временных рядов и других последовательных данных. Она обеспечивает хорошее соотношение между производительностью и сложностью модели, что делает ее популярным выбором во многих приложениях.
Главное преимущество GRU перед LSTM заключается в более низкой сложности и меньшем количестве параметров, что может быть важно при работе с ограниченными вычислительными ресурсами. Однако, стоит отметить, что LSTM всё равно остается более мощным в решении некоторых сложных задач, требующих учета долгосрочных зависимостей.
Давайте рассмотрим пример кода, в котором используется GRU для анализа временного ряда. В этом примере мы будем использовать библиотеку TensorFlow:
```python
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# Генерируем пример временного ряда (синусоида с шумом)
np.random.seed(0)
n_steps = 100
time = np.linspace(0, 10, n_steps)
series = 0.1 * time + np.sin(time) + np.random.randn(n_steps) * 0.1
# Подготавливаем данные для обучения GRU
n_steps = 30 # количество временных шагов в одной последовательности
n_samples = len(series) – n_steps
X = [series[i:i+n_steps] for i in range(n_samples)]
y = series[n_steps:]
X = np.array(X).reshape(-1, n_steps, 1)
y = np.array(y)
# Создаем модель GRU
model = tf.keras.Sequential([
tf.keras.layers.GRU(10, activation="relu", input_shape=[n_steps, 1]),
tf.keras.layers.Dense(1)
])
# Компилируем модель
model.compile(optimizer="adam", loss="mse")
# Обучаем модель
model.fit(X, y, epochs=10)
# Делаем прогноз на будущее
future_steps = 10
future_x = X[-1, :, :]
future_predictions = []









