
Полная версия
Рациональность. Что это, почему нам ее не хватает и чем она важна
Представьте себе забег, в котором участвуют три лошади с равными шансами на выигрыш. Если лошадь № 3 упадет в пятидесяти метрах от старта, шансы каждой из двух оставшихся лошадей составляют уже не один к трем, но один к двум.
Ясно же, заключает он, нет никакого смысла переключаться с лошади № 1 на лошадь № 2. Но это работает не так. Представьте, что после того, как вы сделали ставку на лошадь № 1, Господь возвестил с небес: «Лошадь № 3 не победит». Он мог бы предупредить насчет лошади № 2, но он этого не сделал. Теперь решение поменять ставку не кажется таким уж безумным[46]. В игре «Давайте заключим сделку» в роли бога выступает Монти Холл.
Подобный богу ведущий напоминает нам, насколько сама по себе необычна ситуация парадокса Монти Холла. Для того, чтобы она возникла, требуется всеведущее существо, которое пренебрегает обычной целью коммуникации – сообщать слушателю необходимую ему информацию (в данном случае за какой дверью машина) – и вместо этого стремится подогреть интерес третьих лиц[47]. К тому же, в отличие от реального мира, который никак не соотносит свои подсказки с ходом рассуждений человека, Монти Всемогущий одновременно знает истину и осведомлен о нашем выборе, подгоняя к нему свои откровения.
Невосприимчивость людей к этой полезной, хотя и в некотором роде мистической информации указывает на когнитивную слабость, объясняющую весь парадокс: мы путаем вероятность и предрасположенность. Предрасположенность – это склонность объекта проявлять себя определенным образом. На интуитивном понимании предрасположенностей в основном и строятся наши ментальные модели мира. Люди знают, что согнутая ветка распрямляется, что куду быстро устают, что дикобразы обычно оставляют следы с отпечатками двух подушечек. Предрасположенность нельзя оценить в лоб (ветка либо распрямляется, либо нет), но суждение о ней можно вынести, внимательно изучая физические свойства объекта и используя причинно-следственные законы: более сухая ветка может сломаться; в дождливый сезон куду выносливей; у дикобраза на лапе две подушечки, которые хорошо отпечатываются на мягкой поверхности, но не всегда – на твердой.
Вероятность – дело другое; это абстрактный инструмент, изобретенный в XVII в.[48] У слова «вероятность» несколько значений; но ту вероятность, которая важна при принятии рискованного решения, можно определить как силу нашей убежденности в определенном положении дел при условии, что истинное положение дел неизвестно. Малейший фактор, который меняет степень нашей уверенности в некоем исходе дела, будет менять как вероятность этого исхода, так и рациональный образ действий в сложившихся обстоятельствах. Зависимость вероятности от эфемерного знания, а не от физических свойств объекта объясняет, почему парадокс Монти Холла сбивает людей с толку. Они интуитивно чувствуют, что у автомобиля есть предрасположенность оказаться за любой из трех дверей, и знают, что, открыв одну из них, этой предрасположенности не изменить. Но вероятность не имеет ничего общего с материальным миром – она описывает степень нашего неведения. Новая информация уменьшает неведение и таким образом меняет вероятность. Если эта идея кажется вам мистической или парадоксальной, подумайте о вероятности, что монета, которую я подкинул, упала орлом вверх. Для вас она равна 0,5. Но для меня она равна 1 (я подсмотрел). Одно и то же событие, разное знание, разная вероятность. В парадоксе Монти Холла новой информацией нас снабжает всевидящий Монти.
Это, в частности, объясняет тот странный факт, что, если ведущий снижает уровень нашего неведения более осязаемым способом, проблема решается интуитивно. Вос Савант предложила читателям представить себе телеигру со, скажем, тысячью дверей[49]. Вы выбираете одну, а Монти открывает 998 из оставшихся, и за каждой стоит по козе. Перенесете ли вы свою ставку на ту единственную дверь, которую он не открыл? Если представить дело таким образом, становится очевидно, что выбор Монти снабжает нас полезной информацией. Можно вообразить, как он, решая, какие двери открыть, заглядывает в поисках машины за каждую; закрытая дверь – это знак, что он ее там увидел, и, таким образом, указание на ее местонахождение.
Простая задача на прогнозирование
Выработав привычку сопоставлять числовые значения с событиями, истинность которых неизвестна, мы можем количественно оценить точность своих интуитивных представлений о будущем. Прогнозирование – большой бизнес. Оно важно для политиков, инвесторов, специалистов по оценке рисков и обычных граждан, которым любопытно, что день грядущий нам готовит. Подумайте о перечисленных ниже событиях и запишите свою оценку вероятности наступления каждого из них в ближайшие 10 лет. Многие почти неправдоподобны, поэтому давайте попристальнее всмотримся в нижнюю часть шкалы вероятностей и для каждого из них выберем одно из следующих значений: меньше 0,01 %, 0,1 %, 0,5 %, 1 %, 2 %, 5 %, 10 %, 25 % и, наконец, 50 % и выше.
1. Саудовская Аравия разработает ядерное оружие.
2. Николас Мадуро уйдет с поста президента Венесуэлы.
3. Президентом России станет женщина.
4. Мир пострадает от новой пандемии, которая будет даже смертоноснее ковида.
5. Конституция страны не позволит Владимиру Путину баллотироваться на следующий срок, и вместо него на выборы пойдет его жена, что позволит Путину править страной от ее имени.
6. Массовые забастовки и бунты вынудят Николаса Мадуро уйти с поста президента Венесуэлы.
7. Очередной респираторный вирус передастся в Китае от летучей мыши к человеку и вызовет новую пандемию, которая будет даже смертоноснее ковида.
8. После того как Иран создаст ядерное оружие и проведет подземные испытания, Саудовская Аравия в ответ разработает собственную ядерную бомбу.
Похожие перечни событий я предлагал нескольким сотням респондентов. В среднем люди думали, что сценарий, в котором жена Путина становится президентом России, правдоподобнее сценария, где президентом этой страны становится женщина. Они думали, что вероятность такого развития событий, где забастовки вынуждают Мадуро уйти, выше вероятности его ухода. Они думали, что Саудовская Аравия скорее разработает ядерное оружие в ответ на иранскую бомбу, чем вообще его разработает. Они думали, что вероятность того, что китайская летучая мышь спровоцирует новую пандемию, выше вероятности новой пандемии[50].
Скорее всего, в каком-нибудь из пунктов и вы с ними согласились; по крайней мере, так сделали 86 % участников исследования, оценивавших вероятность каждого из этих предположений. Если я угадал, то вы только что грубо нарушили элементарный закон вероятности, правило конъюнкции: вероятность конъюнкции событий (А и B) должна быть ниже или равна вероятности каждого из них по отдельности (А или B). Например, вероятность вытащить из колоды четную карту масти пики (четная и пики) должна быть ниже вероятности вытащить любую карту масти пики, потому что в колоде есть и нечетные пики.
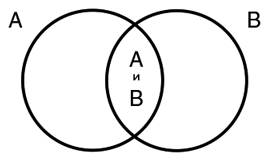
В каждой паре предположений второй сценарий – это конъюнкция событий, одно из которых – событие из первого сценария. Например, «Иран испытывает ядерное оружие, и Саудовская Аравия разрабатывает ядерное оружие» – это конъюнкция, в которую уже входит событие «Саудовская Аравия разрабатывает ядерное оружие», и ее шанс случиться должен быть ниже, потому что есть и другие сценарии, при которых Саудовская Аравия может превратиться в ядерную державу (чтобы противостоять Израилю, чтобы добиться гегемонии в Персидском заливе и так далее). По той же логике отставка Мадуро вероятнее его отставки в результате волны забастовок.
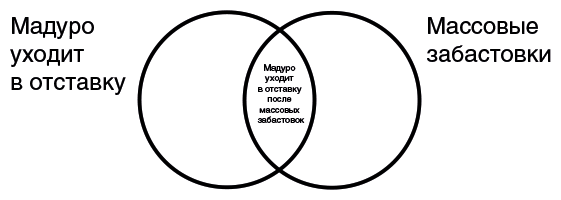
О чем же люди думают, когда так отвечают? Класс событий, описанных одним предложением, выглядит общо и абстрактно, и мозгу просто не за что зацепиться. События, описанные конъюнкцией двух утверждений, кажутся выразительнее, особенно если из них выстраивается сюжет, который мы можем разыграть в театре своего воображения. Интуитивная оценка вероятности опирается на вообразимость: чем легче нам что-нибудь вообразить, тем правдоподобнее оно нам кажется. Так мы попадаем в ловушку, которую Тверски и Канеман назвали ошибкой конъюнкции: конъюнкция двух событий выглядит правдоподобнее, чем каждое из составляющих ее событий по отдельности.
Современные оракулы в своих предсказаниях нередко прибегают к живописному изложению событий – и к черту теорию вероятности[51]. В 1994 г. в журнале The Atlantic вышла нашумевшая статья, написанная журналистом Робертом Капланом и озаглавленная «Грядущая анархия» (The Coming Anarchy)[52]. Каплан пророчил, что в первые десятилетия XXI в. мир охватят войны за дефицитные ресурсы вроде воды; Нигерия сцепится с Нигером, Бенином и Камеруном; развернется мировая война за Африку; США, Канада, Индия, Китай и Нигерия развалятся на части, регионы США, где преобладает испаноговорящее население, откроют границу с Мексикой, а канадская провинция Альберта сольется с американским штатом Монтана; в американских городах вырастет уровень преступности; проблема СПИДа встанет еще острее – и это не считая дюжины других напастей, кризисов и расколов. Статья произвела фурор (и впечатлила даже президента Билла Клинтона, который делился ею с сотрудниками Белого дома), но и число гражданских войн, и доля населения планеты без доступа к питьевой воде, и уровень преступности в Америке камнем идут ко дну[53]. Менее чем через три года после публикации статьи внедрение новых эффективных лекарств от СПИДа привело к резкому сокращению смертности от нее. Спустя более чем четверть века границы стран мира почти не изменились.
Ошибка конъюнкции была впервые проиллюстрирована Тверски и Канеманом – примером, который стал известен под названием «проблема Линды»[54]:
Линде 31 год, она не замужем, очень сообразительна и за словом в карман не лезет. В колледже она изучала философию. В студенческие годы была серьезно озабочена вопросами дискриминации и социальной справедливости, участвовала в демонстрациях против распространения ядерного оружия.
Пожалуйста, оцените вероятность каждого из утверждений:
Линда преподает в начальной школе.
Линда – активистка феминистского движения.
Линда – социальный работник, помогающий психиатрическим больным.
Линда – кассир в банке.
Линда – страховой агент.
Линда – кассир в банке и активистка феминистского движения.
Респонденты полагали, что Линда скорее феминистка и кассир, чем просто кассир: вероятность (А и B) снова оказалась у них выше вероятности отдельно взятого А. Бумерское имя Линда, сомнительный комплимент «сообразительная», ушедшие в прошлое протесты и исчезающие профессии выдают время составления теста – начало 1980-х гг. Но, как известно любому преподавателю психологии, сам результат легко воспроизводится – и сегодня обладающая острым умом Аманда, участвующая в маршах Black Lives Matter, по мнению опрошенных, скорее окажется феминисткой и дипломированной медсестрой, чем просто дипломированной медсестрой.
Проблема Линды особенно ярко высвечивает особенности нашей интуиции. В отличие от задачи выбора, где люди делают ошибки, когда проблема абстрактна («если P, то Q»), и отвечают правильно, когда она привязана к конкретной жизненной ситуации, здесь все испытуемые в теории согласны с абстрактным законом «вероятность (А и В) ≤ вероятности (А)», но путаются, как только формула наполняется конкретным содержанием. Биолог и популяризатор науки Стивен Джей Гулд говорил не только за себя, когда признавался: «Я знаю, что конъюнктивное утверждение – самое маловероятное, но крохотный гомункулус у меня в голове упрямо вопит, подпрыгивая от возбуждения: "Но она не может быть просто кассиром! Прочти описание!"»[55].
Опытные демагоги мастерски используют этого крохотного гомункулуса в своих интересах. Обвинитель, которому не за что зацепиться, кроме трупа, вынесенного волнами на пляж, излагает целую повесть о том, как муж гипотетически мог убить супругу и избавиться от тела, чтобы жениться на любовнице и начать свое дело на деньги, полученные по страховке. Защитник высасывает из пальца альтернативный заезженный сценарий, в котором убитая теоретически могла стать жертвой мелкого воришки, чья попытка стащить кошелек обернулась трагедией. Согласно законам вероятности, каждая добавочная деталь должна уменьшать правдоподобность версии, однако вместо этого она делает ее только убедительнее. Как говорил Пу-Ба, персонаж комической оперы Гилберта и Салливана «Микадо», все это «не более чем подтверждающие детали, призванные придать художественного правдоподобия сухому и неубедительному повествованию»[56].
Правило конъюнкции – базовый закон математической вероятности, и, чтобы его понять, вовсе не обязательно мысленно оперировать числами. Это заставило Тверски и Канемана невысоко оценивать наше интуитивное понимание вероятности, которое, как они писали, основано на стереотипах и жизненном опыте, а не на методичном учете возможностей. Идею, что «внутри каждого бестолкового человека сидит толковый, который пытается выбраться наружу», они отвергли[57].
Другие психологи настроены снисходительнее. Как мы уже убедились, обсуждая парадокс Монти Холла, у слова «вероятность» есть несколько значений, в том числе «физическая предрасположенность», «сила основанного на фактах убеждения» и «частота на длительном промежутке времени». Оксфордский словарь английского языка дает еще одно определение: вероятность – это «видимость истинности или возможность осуществиться, которую любое утверждение или событие имеет в свете имеющихся доказательств»[58]. Столкнувшись с проблемой Линды, испытуемые понимают, что их спрашивают не о «частоте на длительном промежутке времени»: существует только одна Линда, неважно, кассирша-феминистка она или нет. В любой связной беседе рассказчик сообщил бы все эти биографические детали с конкретной целью, а именно: подвести своего собеседника к обоснованному выводу. По мнению психологов Ральфа Хертвига и Герда Гигеренцера, люди, по всей видимости, здраво рассуждают, что в задаче имеется в виду «вероятность» не в каком-нибудь математическом смысле, что требовало бы применить правило конъюнкции, а в смысле «степени уверенности в свете имеющихся фактов», и, понятно, приходят к выводам, к которым предоставленные факты их подталкивают[59].
В пользу такого более благожелательного прочтения говорят и результаты множества исследований, начиная с тех, что проводили сами Тверски и Канеман: когда людей побуждают размышлять о вероятностях в смысле относительной частоты событий, а не заставляют иметь дело с трудноуловимой концепцией вероятности единичного события, они чаще соблюдают правило конъюнкции. Представьте себе тысячу женщин, подобных Линде. Как вы думаете, сколько среди них банковских кассиров? А банковских кассиров и заодно активисток женского движения? Наконец-то гомункулус заткнулся; толковый человек пытается выбраться наружу. Число ошибок конъюнкции резко сокращается[60].
Так не является ли ошибка конъюнкции, типичный пример человеческой слепоты в области вероятности, артефактом двусмысленных формулировок и наводящих вопросов? Тверски и Канеман убеждены, что это не так. Они замечают, что люди совершают ошибку, даже если им предлагают сделать ставку на одну из возможностей (да, большинство ставит на то, что Линда – кассир-феминистка, а не на то, что она кассир). И даже если вопрос переформулирован в терминах частоты, так что люди могут избежать ошибки конъюнкции, окинув мысленным взором банковских кассиров, заметное число опрошенных, хотя и меньшинство, все равно попадается в ту же самую ловушку. Меньшинство превращается в большинство, когда люди оценивают каждую из альтернатив по отдельности, а не вместе и, соответственно, не утыкаются носом в абсурдность ситуации, где подмножество оказывается больше множества[61].
Канеман заметил, что человеческая нерациональность достигает максимума, когда люди отстаивают свои идеи-фикс. Поэтому он предложил новый метод разрешения научных споров, призванный заменить проверенный временем обычай обмена мнениями, в рамках которого оппоненты поочередно двигают вешки и несут ахинею, перекидываясь возражениями и отговорками. В рамках «состязательного сотрудничества» участники дискуссии заранее договариваются о способе эмпирической проверки, призванной положить конец спору, и проводят ее в присутствии приглашенного арбитра[62]. Чтобы выяснить, кто был прав относительно проблемы Линды, Канеман, следуя собственному совету, объединил усилия с Хертвигом; в качестве арбитра они пригласили психолога Барбару Меллерс. Противники договорились провести три исследования, в которых респондентов уже не спрашивали бы об одной-единственной Линде, а задавали бы им вопрос, переформулированный в терминах частоты («Из ста женщин, подобных Линде, сколько…»). Сообщая о неоднозначных итогах, ученые признали: «Мы не рассчитывали, что эксперименты разрешат все загадки; этого чуда и не произошло». Однако стороны согласились, что люди склонны совершать ошибку конъюнкции, даже если имеют дело с частотой. Кроме того, они пришли к выводу, что в благоприятных обстоятельствах – альтернативы можно сопоставлять, а формулировки этих альтернатив не оставляют места воображению – люди способны избежать ошибки конъюнкции.
Чему учат когнитивные иллюзии
Каким же образом рациональность, позволившая нашему виду жить своим умом и в древние времена, и сегодня, уживается в нас с оплошностями и ляпами, которые вскрываются при решении подобных головоломок: предвзятостью подтверждения, чрезмерной самоуверенностью, склонностью отвлекаться на детали и зацикленностью на разговорных привычках? Классические ошибки мышления часто называют когнитивными иллюзиями, и параллели с оптическими иллюзиями – из тех, что печатают на коробках с кукурузными хлопьями и демонстрируют в естественно-научных музеях, – здесь весьма показательны. Смысл этих параллелей гораздо глубже того очевидного факта, что и глаза, и разум иногда нас подводят. Они объясняют, каким образом наш вид может быть таким умным и при этом так легко впадать в заблуждения.
Перед вами две классические иллюзии, придуманные нейробиологом Бо Лотто[63]. Первая – иллюзия светотени. Хотите верьте, хотите нет, но темные полосы на верхней части коробки и светлые полосы спереди на самом деле одинакового серого оттенка.

Вторая – иллюзия формы: углы всех четырех сочленений равны и составляют 90º.
Первый вывод, который нужно сделать: глазам, или, точнее, системе 1 нашего мозга, можно верить не всегда. Второй: увидеть ошибку можно, подключив систему 2, скажем проделав две дырки в каталожной карточке и положив ее поверх первого рисунка или же приложив угол той же карточки к сочленениям, изображенным на втором рисунке.

Но это совсем не повод думать, будто зрительная система человека – дефектный механизм, который постоянно дурачит нас миражами и обманками. Наше зрение – одно из чудес света. Это точный инструмент, способный уловить один-единственный фотон, распознать тысячи форм, провести как по каменистой тропе, так и по высокоскоростной автостраде. Никакие системы машинного зрения не могут сравниться со зрением человеческим – вот почему сейчас, когда я это пишу, беспилотные автомобили не носятся по улицам наших городов, несмотря на десятки лет исследований и разработок. Зрительные модули робокаров иногда путают грузовую фуру с рекламным щитом, а дорожный знак, заклеенный стикерами, с холодильником, набитым продуктами[64].
Иллюзии светотени и формы – это, как говорится, не баг, а фича. Задача зрительной системы – снабдить остальные части мозга точным описанием трехмерной формы и материальных свойств объектов в поле зрения[65]. Это непростая задача, потому что информация, поступающая в мозг с сетчатки глаза, не отражает реальность напрямую. Яркость участка изображения на сетчатке зависит не только от окраски поверхности в реальном мире, но и от интенсивности ее освещения: серый участок может соответствовать как ярко освещенной темной поверхности, так и тускло освещенной светлой (на этом основана иллюзия по хештегу #thedress – #платье, которая прогремела на весь интернет в 2015 г.[66]). Форма изображения на сетчатке зависит не только от трехмерной геометрии объекта, но и от его расположения относительно наблюдателя: острый угол на сетчатке в реальности может быть как острым углом, так и прямым, на который мы смотрим сбоку. Зрительная система компенсирует искажения, делая поправку на интенсивность освещения и преобразовывая углы, чтобы обеспечить остальной мозг описанием, которое соответствует формам и материалам реального мира. Ее промежуточный буфер – двухмерный массив пикселей, поступающих с сетчатки, – скрыт от систем мозга, отвечающих за планирование и рассуждение, потому что он только мешал бы делу.
Благодаря такому устройству наш мозг – не очень хороший экспонометр или транспортир, но ему это и не нужно (если только мы не художники-реалисты). Иллюзии возникают, когда от человека требуют превратиться в такой инструмент – определить яркость полоски и величину угла на картинке. Эти картинки разработаны специально, чтобы простые характеристики – одинаковая яркость, прямые углы – были спрятаны в промежуточном буфере, который сознание обычно игнорирует. Если бы нас спрашивали о предметах реального мира, изображенных на картинке, наше впечатление было бы верным. Серая полоска действительно темнее белой как на освещенной, так и на теневой стороне коробки; ребра, размещенные под разными углами к наблюдателю, действительно спаяны под разными углами.
То же самое касается и когнитивных иллюзий, описанных в этой главе: они могут возникать по той причине, что мы пропускаем мимо ушей буквальное значение вопроса и пытаемся догадаться, что скорее всего интересовало бы нашего собеседника, происходи разговор в социальной реальности. Арифметические действия над обманчиво простыми числами, проверка предположения, касающегося некоторой совокупности символов, выбор из подсказок, предложенных лукавым и всевидящим ведущим, и ситуация, когда мы позволяем живому описанию подтолкнуть нас к неверному выводу, немного напоминают распознавание углов и оттенков серого на печатной странице. Да, эти иллюзии заставляют нас давать неверные ответы; вот только на самом деле это верные ответы, но на другие вопросы – те, что имеют для нас практическую ценность. Разум, способный интерпретировать намерения собеседника в имеющемся контексте, не назовешь примитивным. Вот почему мы яростно жмем «0» и рычим в трубку: «Оператора!», когда робот на линии техподдержки повторяет список бесполезных вариантов: нам нужен человек, способный понять, зачем мы звоним.
То, что эти иррациональные реакции можно объяснить, не дает нам права идти у них на поводу, как и всегда доверять своим глазам. Наука и техника преумножили возможности зрительной системы, вывели их за рамки, поставленные природой. У нас есть микроскопы для крошечного, телескопы для далекого, фотография для прошлого, искусственное освещение для темноты, дистанционное зондирование для невидимого. А когда мы преодолеваем ограничения той среды обитания, в которой эволюционировали, например движемся очень быстро и на большой высоте, полагаться на ощущения становится смертельно опасно. В обыденной жизни, оценивая расстояния и ориентируясь в пространстве, наш мозг делает поправку на эффекты проективной геометрии, опираясь на сходящиеся линии, исчезающие текстуры и текучие очертания поверхности, по которой мы перемещаемся. Когда летчик болтается на высоте в несколько тысяч метров, между ним и землей нет ничего, кроме пустого пространства, а горизонт скрыт за облаками, туманом или горами, его зрительные ощущения расходятся с реальностью. Если он пилотирует самолет, полагаясь на интуицию, которая не в силах отличить ускорение от гравитации, любая попытка выправить машину только усугубит ситуацию и может за считаные минуты отправить самолет в смертельный штопор, как это случилось с неопытным и самоуверенным Джоном Ф. Кеннеди – младшим в 1999 г. Какой бы замечательной ни была зрительная система человека, здравомыслящий авиатор знает, когда ею нужно пренебречь и довериться приборам[67].
И какой бы замечательной ни была наша когнитивная система, в современных условиях мы обязаны понимать, когда ею нужно пренебречь и довериться приборам – инструментам логики, вероятности и критического мышления, которые преумножают возможности разума, выводя их за рамки, поставленные природой. Если сегодня, в XXI в., полагаться на интуицию, любая попытка стабилизировать ситуацию может только усугубить положение, отправив нашу демократию в смертельный штопор.








