Моделирование рассуждений. Опыт анализа мыслительных актов

Приведенный пример показывает, что при использовании методов индуктивных рассуждений, которые предложил Милль, весьма важную роль играет способ выделения признаков или фактов, с помощью которых описываются ситуации.

Еще один пример связан с ситуациями, показанными на рис. 21. Теперь нас беспокоит реакция зверюшки на тех людей, которых она встречает на улице. У зверюшки хорошее настроение, когда она встречает людей с выражением на лице, как в положительных примерах. И ее настроение становится плохим, когда ей встречаются люди с такими лицами, как на отрицательных примерах. Возникает вопрос о причине появления у зверюшки хорошего настроения при встрече с людьми. Три элемента лица: рот, нос и глаза, полностью характеризуют выражение человеческого лица. Будем обозначать эти признаки как е, ƒ и g, а реакцию зверюшки как h. Поскольку все признаки принимают только два значения, как и реакция зверюшки, то можно (это можно было сделать и в предыдущем примере, но было желание продемонстрировать общий подход, использующий запись в виде предикатных формул) обойтись формулами исчисления высказываний. Будем считать, что е, ƒ и g истинны, если они соответствуют типу рта, носа и глаз человека из первого положительного примера. Будем также считать истинным значение h, соответствующее зверюшке с хорошим настроением. Если выделить ядро сходства у положительных примеров, то оно окажется пустым. Это свидетельствует о том, что причиной хорошего настроения зверюшки не может быть просто конъюнкция каких-то признаков человеческого лица. Выражение причины через признаки должно использовать дизъюнкцию.

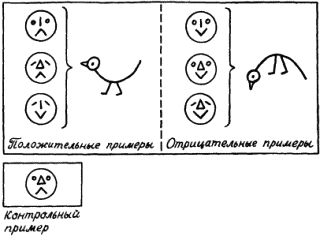
Рис. 21.

В этом случае надо попытаться найти частные ядра сходства и попробовать объединить их в причину через операцию дизъюнкции. Выделим все попарные общие признаки у лиц, входящих в положительные примеры. Первое и второе лицо имеют общую часть е, первое и третье – ƒ, а второе и третье –

. Проверяем, какое из полученных выражений является ложным на всех контрпримерах. Таковым оказывается лишь е. Значит, е должно войти в выражение для причины хорошего настроения зверюшки. Но только два первых положительных примера характеризуются истинным е. Третий положительный пример портит все дело.

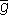
Для того чтобы учесть третий пример, надо построить общее ядро различия для него и лиц, входящих в отрицательные примеры. Сразу видно, что форма рта тут не поможет. Остаются нос и глаза. Нос и глаза такой формы, как в третьем положительном примере, можно по отдельности найти в отрицательных примерах. Но их комбинация, характерная для третьего положительного примера (при принятых нами обозначениях эта комбинация описывается формулой ƒ&

g), нигде не встречается в отрицательных примерах. Это позволяет, наконец, написать выражение для причины h в следующей форме: h=(e

(ƒ&

g)). Словесно эта причинно-следственная связь может быть описана следующим образом: зверюшка находится в хорошем настроении, если она встречает человека, рот у которого печален (концы губ опущены вниз) или глаза у него закрыты, а нос тонкий и прямой.

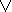
Попробуем теперь найти причину, когда зверюшка бывает в плохом настроении. Обратимся для этого к отрицательным примерам и попробуем на них выделить общее ядро сходства. Оно легко обнаруживается. Это

е. Но, к сожалению, в качестве причины плохого настроения зверюшки его использовать нельзя. Все тот же третий положительный пример препятствует этому. Значит, и для причины плохого настроения зверюшки надо искать дизъюнктивное выражение. Найдем частные попарные ядра сходства. Для первого и второго отрицательных примеров это ядро есть

e&g, для первого и третьего –

е, а для второго и третьего –

e&

ƒ. Второе частное ядро сходства совпадает с общим ядром сходства и поэтому интереса не представляет. Два других частных ядра сходства на всех лицах положительных примеров оказываются ложными. Это позволяет записать выражение для причины плохого настроения зверюшки в следующей форме: h’=((

e&g)

(

e&

ƒ). Учитывая справедливость дистрибутивных законов для конъюнкции относительно дизъюнкции и наоборот (читатели могут проверить этот факт, так как им известно, как проверять в исчислении высказываний равенство ƒ1=ƒ2), можно записать выражение для причины плохого настроения зверюшки в более коротком виде: h’=(

e&(g

ƒ)). Словесно эта причина может быть сформулирована следующим образом: если рот человека улыбается и глаза широко открыты или нос его по форме напоминает картошку, то зверюшка впадает в плохое настроение.

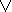
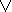
Если составить таблицу, в которой перечислены все комбинации истины и лжи для е, ƒ и g, и определить истинность h и h’, то можно убедиться, что h’=

h. Другими словами, если h истинно, то зверюшка находится в хорошем настроении, а если h ложно, то в плохом. Это означает, что вместо двух выражений для h и h’ можно пользоваться только одним из них.

Такая ситуация не является стопроцентной. На рис. 22 мы снова встречаемся с известной нам зверюшкой. Но здесь выражения для h и h’, легко вычисляемые с помощью общих ядер сходства, имеют вид h=e&

g и h’=g&

e. Другими словами, зверюшка в хорошем настроении, когда встречает человека с печальным ртом, и она печалится, когда видит человека с широко открытыми глазами. В этом случае h и h’ никак не связаны между собой.

Чем различаются два рассмотренных случая? Пусть на пути нашей зверюшки встретился человек с лицом, обведённым на рис. 21 и 22 в рамочку. Как среагирует на него зверюшка? В случае, показанном на рис. 21, она тут же перейдет в хорошее настроение, ибо h истинно, а h’, естественно, ложно. Но в случае, соответствующем рис. 22, ситуация для зверюшки становится весьма сложной. Для встретившегося ей персонажа h и h’ одновременно ложны. Возникает конфликт. Новый персонаж не укладывается в ту классификацию, которая была построена по положительным и отрицательным примерам. Конфликт для зверюшки неразрешим.

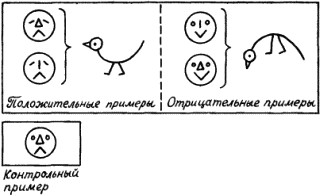
Рис. 22.

Его можно разрешить лишь волевым усилием. Надо включить новый персонаж в число либо положительных, либо отрицательных примеров. В реалии разбиение чего-либо на классы (в наших случаях на два класса) вытекает из каких-то прагматических требований. Например, все люди, отнесенные к положительным примерам, относятся к зверюшке доброжелательно. Их не нужно опасаться. А люди, относимые к группе отрицательных примеров, таковы, что лучше обойти их стороной. От них ждать добра не приходится. Тогда волевое отнесение нового персонажа к той или иной категории должно получить практическое подтверждение своей правильности или неправильности. Если встреча с ним для зверюшки окажется благоприятной, то его, конечно, надо относить к положительным примерам. В противном случае его место среди отрицательных примеров.

Мы продемонстрировали весьма важное положение, связанное с процессом индуктивного обобщения. Если h и h’ классифицируют множества положительных и отрицательных примеров, так что h=

h’, то появление новых примеров не ставит систему в тупик. Она всегда куда-то отнесет новый случай, т. е, при выполнении указанного равенства система обладает полнотой классификации. Конечно, может оказаться, что эта классификация не является правильной. Ведь она построена по неполному множеству представителей положительного и отрицательного классов.

Пусть, например, мы снова имеем классификацию, которая соответствует ситуациям, показанным на рис. 21. Но контрольный пример поступает в систему с указанием, что он относится к группе отрицательных примеров. А система в соответствии с ранее построенной классификацией относит его к положительному классу. В таком случае необходимо внести коррективы в классификацию, полученную ранее, выработать новую классификацию с учетом нового множества отрицательных примеров.

Вывод из этого только один. Поскольку множества положительных и отрицательных примеров не охватывают всех возможных случаев, то h и h’, построенные по методам Милля, даже в тех случаях, когда h=

h’ не могут быть абсолютно точными. Эти утверждения могут быть приняты лишь с некоторой оценкой истинности Q(h) (соответственно Q(h’)). Но прежде чем описать, как эти оценки вычисляются, рассмотрим еще один метод правдоподобных рассуждений.

Рассуждения по аналогии

Начнем с задачи. Посмотрим на первую строку, показанную на рис. 23. В этой строке представлено преобразование F, с помощью которого пара слов, стоящая слева от стрелки, преобразуется в слово, стоящее от нее справа. Можно ли угадать, во что превратится пара слов, стоящих во второй строке на этом рисунке, если считать, что преобразование F’ максимально похоже на преобразование F? Для ответа на этот вопрос надо сначала понять, какова суть F. После недолгого размышления можно прийти к выводу, что слово, получаемое в результате преобразования, устроено следующим образом: первая его половина совпадает с первой половиной первого слова в исходной паре, а вторая его половина получается из первой половины второго слова в исходной паре, если в ней сделать перестановку букв. Если мы верим, что F именно таково (еще раз обратим внимание на этот постулат веры), то можно попытаться придать F’ тот же смысл. Тогда вместо знака вопроса в правой части второй строки можно написать результат преобразования. Им будет слово «плен». Если считать, что F’’ – преобразование, аналогичное F и F’, то вполне законным будет получение правой части по паре левых и в третьей строке на этом рисунке.

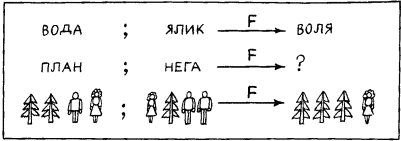
Рис. 23.

Какой смысл мы вложили в слово «аналогичное», когда говорили о преобразованиях? По крайней мере, двоякий. Во-первых, мы предположили, что элементы, из которых состоят слова и рисунки, как-то соответствуют друг другу. Например, елочки и фигурки из третьей строки ассоциируются у нас с буквами, из которых состоят слова, а буквы важны не сами по себе, а по тому месту, которое они занимают в словах. Во-вторых, мы предполагаем, что сохраняется суть преобразования, хотя элементы, с которыми преобразование оперирует, могут быть другими.

Эти соображения помогают уловить расплывчатый смысл, вкладываемый людьми в понятие аналогии. На рис. 24 показано три преобразования для треугольника Т. Преобразование

можно назвать обобщением. При переходе от треугольника к многоугольнику наследуются только те геометрические свойства, которые верны для любых многоугольников. Сам треугольник по отношению к множеству многоугольников представляет некоторую конкретизацию. На рис. 24 преобразованием конкретизации служит

, переводящее произвольный треугольник в его частный вид – прямоугольный треугольник. А вот преобразование

можно назвать преобразованием по аналогии. Треугольная пирамида сохраняет многие свойства треугольника, но является не плоской, а объемной фигурой.

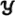
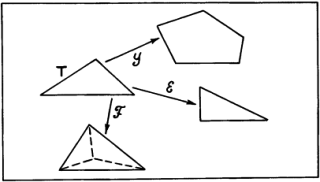
Рис. 24.

Первая попытка формализовать понятие рассуждения по аналогии была предпринята Лейбницем. В своем сочинении «Фрагменты логики» он ввел понятие пропорции для отношения аналогии. Пропорция Лейбница формулируется следующим образом: «Вещь А так относится к вещи В, как вещь А’ к вещи В’». Обычно пропорцию Лейбница представляют в виде диаграммы:

Для иллюстрации того, как может быть использована диаграмма Лейбница, рассмотрим семантическое пространство Осгуда. Это пространство, которое американский психолог Чарльз Осгуд строил экспериментально, проводя опыты с людьми, должно было, по его мнению, характеризовать организацию размещения информации в памяти человека. Мы не будем здесь останавливаться на способе его построения. В комментарии к данному разделу имеется некоторая информация по этому вопросу, а в библиографии заинтересовавшиеся читатели могут найти нужные работы. Скажем только, что упрощенное пространство Осгуда является обычным трехмерным евклидовым пространством. Близость по метрике этого пространства характеризует семантическую близость понятий, фактов и утверждений, а рассуждения, проведенные в пространстве относительно группы элементов, могут проецироваться по аналогии на группы, состоящие из семантически близких элементов.

Проиллюстрируем эту мысль, взяв «кусок» пространства Осгуда, относящийся к понятиям, используемым для указания родства. То, что они в семантическом пространстве расположены компактно, было доказано экспериментально. Этот «кусок» пространства Осгуда показан на рис. 25. Для удобства введена система координат и сделано такое преобразование, чтобы все точки, соответствующие интересующим нас понятиям, оказались лежащими в вершинах единичного куба (правомочность такого преобразования в пространстве Осгуда мы тут не обсуждаем).

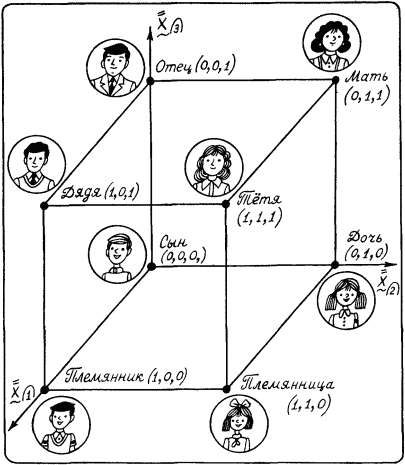
Рис. 25.

Пусть даны три элемента пропорции Лейбница А, А’ и В. И необходимо узнать элемент В’. Для рассматриваемого примера примем следующий способ нахождения координат понятия В’: b’i=bi+а’i–аi где i=1,2,3. Пусть, например, нас интересует пропорция Сын:Дочь=Дядя:? Для определения неизвестного члена пропорции произведем необходимые вычисления, используя координаты понятий, отмеченные на рис. 25. Получим b’1=0+1–0=1; b’2=1+0–0=1; b’3=0+1–0=1. Таким образом, понятие В’ имеет координаты (1,1,1). Этим координатам соответствует понятие «Тетя».

Для дальнейшего необходимо уточнить понятия «похожесть» и «аналогия», использованные в диаграмме для пропорции Лейбница, и придать им по возможности строгий смысл. Сделать это можно следующим образом. Выберем некоторый алгебраический язык для описания A и В, который обозначим

1 и некоторый (вообще говоря, другой) алгебраический язык для описания А’ и В’, который обозначим

2. Переход от A к В и от A’ к B’ будем интерпретировать как преобразование соответствующих описаний в языках

1 и

2. Поскольку выбранные языки являются алгебраическими, то в них выделены элементы и операции, определённые над этими элементами. Учитывая дальнейший пример, будем считать, что в качестве элементов языков

1 и

2 выступают некоторые изображения или их совокупности, связанные отношениями из заданного набора двуместных отношений. А операции состоят в том, что над элементами можно совершать различные геометрические преобразования, определяемые их движениями. Это приводит к изменению отношений между элементами, входящими в анализируемые совокупности.

Чтобы все сказанное стало понятнее, рассмотрим конкретный пример. На рис. 26 показана серия изображений, соответствующая пропорции Лейбница, в которой, как всегда, надо восстановить недостающее звено, т.е. осуществить (если это возможно) вывод по аналогии. Для описания изображений введем языки

1 и

2. В языке

1 в качестве элементов возьмем изображение солнца s, и человечка m. В качестве отношений будем рассматривать отношения R1 – «быть слева вверху» и R2 – «быть справа вверху». Тогда ситуация А может быть описана как sR1m. В качестве операций в

1 будем использовать перестановку объектов относительно друг друга O1 и вращение на 180° по часовой стрелке O2. Тогда преобразование F можно описать как O1(s,m); O2(m). В результате этого возникает ситуация B, описание которой в языке

1 выглядит как sR2(O2(m)).

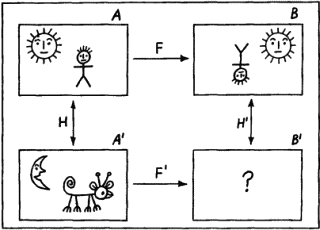
Рис. 26.

Введем теперь элементы языка

2. Это луна l и фантастическое животное q. В качестве отношений, используемых в

2, возьмем снова отношения R1 и R2, а в качестве операций

2 сохраним операции O1 и O2 языка

1. Описание А’ выглядит следующим образом: lR1q. Для получения описания В’ установим между А и А’ отношение взаимно однозначного соответствия H, например, так, что имеют место взаимно однозначные соответствия s

l и m

q. Тогда sR1m

lR1q и А

А’. Преобразование F’ в наших предположениях совпадает с F. Значит, В и В’ должны находиться также во взаимно однозначном соответствии. Но В есть sR2(O2(m)). Учитывая соответствие между элементами

1 и

2, выводим описание для В’:lR2(O2(q)).

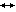
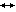
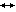
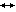
Рассмотренная процедура носит общий характер. Можно строго доказать, что если в пропорции Лейбница А, А’ и В описаны с помощью алгебраического языка, использующего лишь двуместные отношения, задан характер преобразований F и установлено взаимно однозначное соответствие между

1 и

2, то описание В’ также возможно на языке

2 и существуют взаимно однозначные соответствия F

F’ и В

В’, так что, применяя к А преобразование F и к А’ преобразование F’, получаем В и В’, такие, что В

В’.

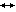
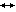
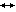
Заметим, что из этого утверждения вытекает, что необходимым условием для возможности рассуждений по аналогии с использованием пропорции Лейбница служит требование коммутативности ее диаграммы. Требование коммутативности диаграммы означает, что описание В’, полученное из A с помощью F и взаимно однозначного соответствия H’, ничем не отличается от описания В’, полученного из A с помощью взаимно однозначного соответствия H и последующего применения к этому результату преобразования F’. С требованием коммутативности диаграмм мы еще столкнемся в последующих разделах этой главы.

Несмотря на все сказанное, полное описание модели рассуждений по аналогии всё еще не получено, так как пропорция Лейбница явно не исчерпывает всех случаев рассуждений подобного типа. Да и в случае, когда мы имеем дело действительно с пропорцией Лейбница, остаются нерешенными по крайней мере два вопроса: как построить языки

1 и

2 и как установить взаимно однозначное соответствие между ними. Возможные в этом случае трудности иллюстрирует рис. 27. На этом рисунке показаны ситуации А и А’. Ситуация А может быть описана следующим текстом: «Ромео любит Джульетту. Джульетта любит Ромео (на рис. 27 это отношение R1). Ромео мужчина (R2). Он итальянец (R3). Джульетта женщина (R4). Она красива (R5). Она не замужем (R6)». Ситуация А’ может быть описана следующим текстом: «Тристан любит Изольду. Изольда любит Тристана (R1). Тристан мужчина (R2). Он бретонец (R*2). Изольда женщина (R4). Она красива (R5). Она замужем (R*6). Ее муж – король Марк (R7)».