 полная версия
полная версияМоделирование рассуждений. Опыт анализа мыслительных актов
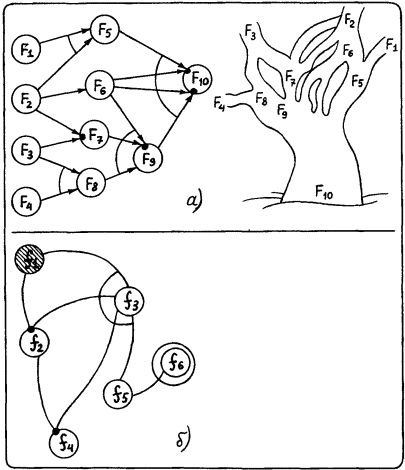
Рис. 19.
Дерево вывода с такими условиями переходов от вершины к вершине носит название И-ИЛИ дерева. В И-ИЛИ дереве ориентация дуг показывает направление вывода. Естественное разбиение вершин дерева по ярусам отражает глубину вывода (число шагов, необходимых для получения утверждений данного яруса). Первый ярус дерева образуют вершины (на рис. 19, а это вершины F1, F2, F3, F4), играющие роль аксиом или утверждений, истинность которых задается извне.
Схема вывода не обязательно описывается в виде дерева. Она может иметь вид произвольной сети, ориентированной, неориентированной или частично ориентированной. На рис. 19, б показан пример неориентированной сети. Такая сеть (наличие или отсутствие ориентации не играет здесь роли) называется И-ИЛИ сетью. Процесс вывода на И-ИЛИ сети протекает следующим образом. Пусть мы хотим доказать утверждение ƒ6 (на рис. 19, б этому соответствует целевая вершина). В качестве априорно доказанного задано утверждение ƒ1 (ему соответствует начальная вершина, которая на рис. 19, б заштрихована). Как из ƒ1 можно получить ƒ6? Если считать, что все связи допускают ориентацию в нужную сторону, то из ƒ1 можно получить ƒ3, затем ƒ5 и, наконец, ƒ6. Но этот путь нам удалось отыскать потому, что сеть, показанную на рис. 19, б, мы видим «с птичьего полета». Лабиринт поиска лежит в виде чертежа перед нами. Именно это позволяет нам не делать лишних попыток, не двигаться в ненужную сторону, а идти кратчайшим путем к цели.
Подобная ситуация приятна, но редко встречается в действительности. При решении любой задачи, даже если заранее известен ее ответ, к которому надо стремиться (для школьника эта ситуация с подглядыванием в ответ до решения задачи весьма типична), мы не видим перед собой полного лабиринта возможностей. Мы пытаемся построить этот лабиринт, видя лишь начальные «площадки лабиринта» и не зная, что лежит между ними и «целевыми площадками». В нашем примере мы стоим на начальной площадке, в вершине ƒ1, и не знаем, куда идти. Мы делаем попытку перейти в ƒ2 (т.е. вывести утверждение), но видим, что этого нельзя сделать. Тогда мы движемся в сторону утверждения ƒ3 и обнаруживаем, что его доказательство возможно. Теперь в нашем распоряжении две площадки лабиринта: ƒ1 и ƒ3. Из ƒ3 можно двигаться в четырех направлениях. Одно из них, ведущее назад к ƒ1, интереса не представляет. Попытка продвинуться к ƒ2 и ƒ5 оказывается успешной. Возникает новый фронт достигнутых площадок (доказанных утверждений). Теперь его образуют ƒ2, ƒ3 и ƒ5. Площадка ƒ1 исключается из активного фронта, так как использованы все связи этой площадки с другими площадками лабиринта. На следующем шаге достигаются площадки ƒ4 и ƒ6. Наличие среди доказанных выражений целевого ƒ6 позволяет завершить процесс доказательства. После этого можно произвести «чистку», в результате которой останется лишь тот путь, который кратчайшим образом приводит от начального утверждения ƒ1 к целевому ƒ6.
На примере мы описали процедуру, которая, как легко видеть, носит универсальный характер и пригодна для поиска пути вывода в лабиринтах произвольного типа. Эта процедура известна среди специалистов под названием метода прямой волны. Волна поиска путей к целевой площадке распространяется от всех площадок, играющих роль начальных.
Возможен и другой способ поиска доказательства. Он носит название метода обратной волны. В этом методе волна начинает свое движение от целевых площадок и движется в направлении начальных площадок лабиринта. Для нашего случая на первом шаге была бы порождена площадка, соответствующая ƒ5, вслед за этим ƒ3 и ƒ1. На этом движение волны прекратилось бы, так как ее фронт достиг всех (в данном случае единственной ƒ1) начальных площадок.
Различие между прямой и обратной волной состоит в том, что они порождают в процессе своего движения различные промежуточные «фронты» площадок, что приводит к различному числу шагов при поиске. Часто используется смешанный метод вывода, при котором одновременно движутся прямая и обратная волны. При встрече этих волн формируется путь вывода от начальных аксиом к целевым выражениям.
Несколько иной разновидностью схем вывода являются так называемые альтернативные деревья или альтернативные сети. В этих схемах выбор дальнейшего пути движения зависит от того, достигнут или не достигнут вывод некоторого выражения. Другими словами, попытки продвижения по лабиринту, которые мы демонстрировали на методе прямой волны при удачах и неудачах, могут влиять на стратегию дальнейшего движения. Такие схемы вывода мы более подробно рассмотрим в пятой главе. Здесь же лишь проиллюстрируем рассуждение такого типа на примере.
В знаменитом рассказе «Убийство на улице Морг» Эдгара По сыщик-любитель Огюст Дюпен помещает в газете объявление о находке орангутанга, который, по слухам, принадлежит матросу мальтийского корабля. На вопрос о причинах такого объявления Огюст Дюпен отвечает следующим образом:
«Но вот обрывок ленты, посмотрите, как она засалена, да и с виду напоминает те, какими матросы завязывают волосы. К тому же таким узлом мог завязать ее только моряк, скорее всего мальтиец. Я нашел эту ленту под громоотводом. Вряд ли она принадлежала одной из убитых женщин. Но даже если я ошибаюсь и хозяин ленты не мальтийский моряк, то нет большой беды в том, что я сослался на это в моём объявлении. Если я ошибся, матрос подумает, что кто-то ввел меня в заблуждение, и особенно задумываться тут не станет. Если же я прав, – это козырь в моих руках. Как очевидец, хоть и не соучастник убийства, француз, конечно, не раз подумает, прежде чем пойти по объявлению. Но вот он станет рассуждать: „Я не виновен, к тому же я человек бедный; орангутанг и вообще-то в большой цене, а для меня это целое состояние, зачем же терять его из-за пустой мнительности. Вот он, рядом, только руку протянуть. Его нашли в Булонском лесу, далеко от места, где произошло убийство. Никому в голову не придет, что такие страсти мог натворить дикий зверь. Полиции ввек не догадаться, как это случилось. Но хотя бы обезьяну и выследили – попробуй докажи, что я что-то знаю; а хоть бы и знал, я не виноват. Главное, кому-то я уже известен. В объявлении меня так и называют владельцем этой твари. Кто знает, что этому человеку еще про меня порассказали. Если я не приду за моей собственностью, а ведь она больших денег стоит, да известно, что хозяин – я, на обезьяну падет подозрение. А мне ни к чему навлекать подозрение, что на себя, что на эту бестию. Лучше уж явлюсь по объявлению, заберу орангутанга и спрячу, пока все не порастет травой“».
Читателю предлагается построить по этому тексту альтернативное дерево рассуждений владельца орангутанга.
И последнее замечание к тексту этой главы. Конечно, не надо считать дедуктивные схемы рассуждений панацеей для всех случаев. Метод, обычно приписываемый Шерлоку Холмсу, не всегда ведет к успеху.
Для многих читателей имя Шерлока Холмса навсегда связано с изяществом и неоспоримостью дедуктивного метода рассуждений. Но при внимательном чтении произведений Конан-Дойля легко обнаружить, что знаменитый сыщик пользовался не только дедуктивными рассуждениями. Шерлок Холмс никогда не забывал и об индукции.
Всякое порождение новой версии – это индуктивный шаг. Дедукцией является лишь обоснование выдвинутой версии. А выдвижение новых версий тесно связано с переходом от некоторых частных фактов к общим утверждениям относительно их, т.е. с правдоподобными рассуждениями. И настало время перейти к их обсуждению.
Глава четвертая. АВТОМАТИЗАЦИЯ ПРАВДОПОДОБНЫХ РАССУЖДЕНИЙ
Я гнет бездарности тащусквозь мир красот и безобразий.Всегда, везде, во всем ищупричинно-следственные связи.С.А. СтебаковОт Аристотеля до Бэкона
Аристотель упоминал о двух основных процессах рассуждений: нисходящем или дедуктивном и восходящем или индуктивном. Иногда говорят, что дедукция – это рассуждение «от общего к частному», а индукция – «от частного к общему». При таком понимании этих двух процессов возникает иллюзия, что они как будто обратны друг другу и одну схему рассуждений можно получить из другой прямым обращением. Этой иллюзии поддался и Аристотель. Увлеченный красотой и стройностью воздвигнутого им здания силлогистики, он попытался втиснуть в его объемы и индуктивное рассуждение, ввести схему индуктивного силлогизма. Но здесь его подстерегала неудача. Индуктивные рассуждения никак не хотели отливаться в ту стройную форму, которая так подошла дедуктивным рассуждениям.
Попытки адептов учения Аристотеля исправить, уточнить, расширить понятие индуктивного силлогизма остались тщетными. В основе различия дедукции и индукции лежало нечто более существенное, чем думали мыслители, не желавшие выходить за рамки мира, очерченного рукой гениального Аристотеля.
Напомним еще раз основную цель, которую преследовал Аристотель, создавая силлогистику. Она должна была стать непобедимым оружием в споре. Если оппонент признавал общее положение, относящееся к классу однородных объектов или явлений (а как он мог не признать, например, столь очевидную истину, что «Все люди смертны»), и принадлежность какого-либо объекта или явления к этому классу (например, что «Сократ есть человек»), то ему ничего не оставалось сделать, как признать, что общий для всего класса признак переносится и на отдельный элемент этого класса. Возражать против такого хода рассуждений мог бы только человек, спорить с которым не имеет никакого смысла, ибо он отвергает очевидное.
Если бы аналогичная цель стояла перед спорящим, который пользуется методом индукции, то схема его рассуждений должна была быть следующей. Сначала он мог бы сообщить оппоненту несколько утверждений об отдельных представителях класса, в существование которого должны верить оба спорящих. Каждое такое утверждение должно касаться одного и того же признака, связанного с элементами этого класса (например, оппоненту надо было сообщить, что «Гомер смертен», «Фидий смертен», «Эзоп смертен», и добиться от оппонента признания правильности этих утверждений). После этого надо было прийти с противником к согласию, что все эти элементы принадлежат одному классу (в нашем примере, что Гомер, Фидий и Эзоп являются людьми). Далее нужно было совершить главный индуктивный шаг, перейти к утверждению о классе (т.е. ввести утверждение «Все люди смертны») и заставить противника принять это утверждение.
Трудность таится именно на последнем шаге спора. Примет или не примет этот шаг оппонент, зависит от степени его уверенности в правильности данного шага. Этот шаг требует не умения логически обосновывать свои действия и рассуждения, а веры в свою справедливость. Можно ли от трех конкретных утверждений о Гомере, Фидии и Эзопе перейти к общему утверждению о всех людях? Ответ на этот вопрос не снимается, если мы к названным трем великим представителям греческой культуры добавим еще кого-нибудь. Где граница, после которой индуктивный шаг станет оправданным? Ответа на этот вопрос нет и быть не может. Именно поэтому индуктивное умозаключение всегда является правдоподобным рассуждением. Его надо принимать на веру. И обсуждать можно только то, как оценить обоснованность этой веры, т.е. как оценить степень правдоподобности выведенного утверждения.
Мы получили весьма важный вывод о том, что каждое правдоподобное утверждение А должно сопровождаться некоторой оценкой правдоподобности (достоверности) Q(A). Интерпретация Q(A) может быть различной. Некоторые из них, сейчас наиболее распространенные, будут обсуждены в последующих разделах этой главы.
Подчеркнем еще раз принципиальное различие между дедуктивной и индуктивной схемами рассуждений. Если посылки в дедуктивной схеме выбраны правильно, являются истинными, то получаемые с их помощью заключения не могут быть ложными. Если они нас чем-то настораживают, вызывают недоумение, то надо еще раз проверить истинность посылок. Убедившись в их правоте, ничего не остается делать, как полностью принять следующие из них выводы. Если посылки в индуктивной схеме выбраны правильно, являются истинными, то получаемые с их помощью заключения могут быть как истинными, так и ложными. Та или иная точка зрения на заключения зависит от степени субъективной уверенности в достаточности посылок для получения заключения. Именно поэтому вместо оценки истинности или ложности заключения в правдоподобных рассуждениях используется оценка правдоподобности (или истинности) Q(A).
Известный специалист по психологии восприятия Р. Грегори писал:
«В самой природе дедуктивных утверждений содержится нечто в высшей степени странное. Дедукция оперирует формальным символическим алфавитом. Мы вправе сказать, что дедукция небиологична, поскольку ее не могло быть до появления формального языка. В связи с этим чрезвычайно заманчива мысль об индуктивной природе процесса решения проблем, который сопровождает работу воспринимающего мозга, и о переходе к дедукции в работе мозга, занятого абстрактным мышлением, передачей сообщений, выполнением расчетов. Если это верно, то дедукция окажется свойственной только мозгу человека, поскольку лишь человек обладает формальной речью. Но это можно отнести также к электронным вычислительным машинам, работа которых подчинена правилам некоторого формального языка. …По-видимому, можно утверждать, что – поскольку в отличие от владения формальной речью восприятие не является исключительной привилегией человека – перцептивные процессы в своей сущности не дедуктивны. Остается принять, что они индуктивны».
Таким образом, индукция тесно связана с восприятием, опытом. Когда в развитии научного мировоззрения возник этап понимания, что опытные данные, эксперимент, реальная деятельность по достижении определенных целей служат единственным мерилом обоснования научных построений, тогда наступила пора индукции.
Понимание роли индуктивных рассуждений в научном познании связано с именем двух людей, носивших одинаковую фамилию. Один из них, Роджер Бэкон, был францисканским монахом и выдающимся мыслителем. С целью прославления церкви и воплощения своей мечты о том, что католическая церковь должна царить над всем миром, этот монах в 1265 году посвятил папе Клименту IV свою работу, где сделал набросок новой экспериментальной науки, которая должна была дать в руки человечества инструмент к познанию природы и роли высшего разума в ее существовании. Только через опыт возможно постижение истины – к такому выводу пришел Роджер Бэкон. И, критикуя метод Аристотеля, он писал: «Было бы лучше сжечь сочинения Аристотеля и начать все сызнова, нежели принимать его заключения без проверки».
Но францисканец поспешил. В XIII веке схоластическая наука еще не собиралась сдавать свои позиции. Аристотель считался вершиной научной мысли. И надо было дожидаться XVII века, когда человек, обладавший большой политической властью и непревзойденным красноречием, лорд Веруламский Фрэнсис Бэкон опубликует свой труд под красноречивым и недвусмысленным названием Novum Organum[7]. В этой работе философ обратил внимание ученых на важность экспериментального метода в науке. Мысль о том, что всякое научное положение, полученное в теории, должно подтверждаться практикой, сформулирована им четко и исчерпывающе. Фрэнсису Бэкону повезло куда больше, чем его однофамильцу. Он высказал свои мысли в нужное время, когда экспериментальная наука начала победное шествие по миру. И за это он стал признанным отцом нового направления в научном познании.
Но если внимательно разобраться в сочинениях Фрэнсиса Бэкона, то в них вряд ли удастся обнаружить пропагандируемый им метод индуктивного развития науки. Ничего подобного силлогистике Аристотеля у него нет. А поэтому вплоть до середины XIX века в области индуктивных рассуждений ничего не менялось. Их теории просто не существовало.
Индукция Джона Стюарта Милля
В процессе наблюдения за окружающим миром мы решаем две главные задачи, связанные с созданием модели, его описывающей. Прежде всего мы выделяем в наблюдаемом некоторые сущности. В логике им соответствуют некоторые понятия. А кроме того, мы устанавливаем между этими понятиями определенные отношения. Эти отношения могут быть как наблюдаемыми непосредственно с помощью наших органов чувств (например, отношения типа «субъект-действие» или «быть раньше»), так и достраиваемыми на основании некоторой «логики знаний» (например, отношения типа «причина – следствие» или «цель – средство»).
Среди всех этих отношений едва ли не главнейшую роль для познания окружающего мира играют каузальные отношения, отражающие в наиболее общей форме связи причин и следствий. Подробный разговор о каузальных связях мы отложим до конца этой главы. А пока поговорим лишь о том их виде, внимание к которому привлекли исследования английского логика середины XIX века Джона Стюарта Милля. Он поставил перед собой задачу нахождения связей между фактами и явлениями на основе анализа их совместного появления или непоявления в последовательности экспериментов. При этом он принял меры к тому, чтобы не повторять знаменитой ошибки при установлении причинно-следственных связей, которая вошла в историю науки под названием Post hoc ergo propter hoc, т.е. «После этого, значит вследствие этого». А ошибки такого типа не только встречались и встречаются в бытовых человеческих рассуждениях до сих пор, но иногда подобные выводы делаются сознательно, например, для создания неожиданных поэтических образов. Вот как превосходно использовал этот прием В. Луговской: «Речные девки в речках мочут косы, и над Русью от этого подъемлется туман».
Принципы установления причинно-следственных отношений, которые предложил Милль, основываются на идеях выделения сходства и различия в наблюдаемых ситуациях внешнего мира.
Способность улавливать сходство и выделять различия – фундаментальная способность, по-видимому, всех живых существ. Опираясь на эту способность, Милль сформулировал свои принципы индукции.
Первым из них является Принцип единственного различия. В формулировке, которая дана в известном учебнике логики В. Минто, он звучит следующим образом: «Если после введения какого-либо фактора появляется, или после удаления его исчезает, известное явление, причем мы не вводим и не удаляем никакого другого обстоятельства, которое могло бы иметь в данном случае влияние, и не производим никакого изменения среди первоначальных условий явления, то указанный фактор и составляет причину явления».
Схематически этот принцип можно описать в виде следующей схемы:
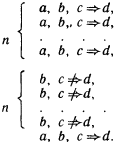
Здесь знак
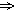
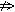
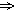
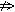
Второй основополагающий принцип индуктивного рассуждения Милля носит название Принципа единственного сходства. В формулировке того же В. Минто он звучит следующим образом: «Если все обстоятельства явления, кроме одного, могут отсутствовать, не уничтожая этим явления, то это одно обстоятельство находится в отношении причинной связи с явлением при условии, что приняты были все меры к тому, чтобы никаких других обстоятельств, кроме принятых во внимание, налицо не оказалось».
Схематическое представление этого принципа Милля выглядит следующим образом:

В этой схеме все примеры являются положительными. Из нее по Принципу единственного сходства вытекает, что a и d связаны причинно-следственным отношением.
Еще один принцип Милля – Принцип единственного остатка. Он формулируется В. Минто следующим образом: «Если вычесть из какого-либо явления ту часть его, которая согласно прежним исследованиям оказывается следствием известных причин, присутствующих в явлении причин, то остаток явления есть следствие остальных причин».
Принцип единственного остатка можно проиллюстрировать следующей схемой:
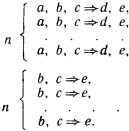
Следовательно, a и d связаны причинно-следственным отношением, а b и с являются возможными причинами е. Для дальнейшего уточнения зависимости надо посмотреть, приводит ли исключение b к появлению e. Если приводит, то отношением «причина – следствие» связаны между собой с и е. В противном случае это отношение имеется между b и е.
Отметим ряд особенностей схем Милля. Прежде всего, они справедливы лишь при условии, что в описании ситуации имеется полное множество наблюдаемых фактов или явлений. Например, в последнем случае может оказаться, что и исключение b, и исключение с не влияют на появление е. Тогда можно предположить, что для появления е необходимо либо одновременное наличие b и с, либо е вызывается чем-то, не вошедшим в описание ситуации.
Другими словами, появление некоторого элемента ситуации может определяться не отдельными факторами или элементами, а их совокупностью, задаваемой с помощью сложного логического выражения. В левой части причинно-следственного отношения может стоять сложное выражение, в котором отдельные элементы могут быть связаны между собой конъюнктивными и (или) дизъюнктивными связками.
Проиллюстрируем это на следующих примерах. В качестве первого примера рассмотрим ситуации, показанные на рис. 20. С ними связана следующая история. Когда некий человек встречает на улице необычных зверюшек, то, глядя на них, он или радуется, или печалится. Нас интересует, какие качества зверюшек приводят человека в хорошее расположение духа. Другими словами, что является причиной его улыбки. Для удобства ответа на этот вопрос на рис. 20 положительные примеры и контрпримеры разделены штриховой чертой.

Рис. 20.
Как видно из рисунка, зверюшки обладают тремя признаками: формой спины, числом ног и формой ног. Что же вызывает улыбку? Используем метод Милля. Возьмем в качестве первой возможной причины форму спины у зверюшки. Положительные примеры таковы, что во всех наблюдаемых случаях эта форма выгнута вниз. Обозначим этот признак через a, а реакцию человека, когда он радуется, через d. Можно ли утверждать, что а есть причина d? Согласно Принципу единственного сходства наличие спины такой формы должно всегда вызывать улыбку. Но первый же контрпример опровергает это. Число ног (обозначим этот признак как b) также не может быть причиной улыбки. В положительных примерах b везде равно двум, и можно подумать, что именно две ноги зверюшки веселят человека. Но в трех контрпримерах ног тоже две. С формой ног (этот признак обозначим как с) ситуация в положительных примерах такова, что сразу ясно, что с не может быть причиной d.
Таким образом, ни один из признаков зверюшки по отдельности не может быть причиной улыбки человека. Попробуем выделить общее ядро сходства у всех зверюшек в положительных примерах. Такое ядро есть. Все зверюшки в этих примерах имеют выгнутую вниз спину и две ноги. Другими словами, для них всегда истинно утверждение Р1(а)&Р2(b), в котором Р1(а) – предикат, интерпретируемый как «форма спины, выгнутая вниз», а Р2(b) – предикат, интерпретируемый как «число ног равно двум». Проверим, будет ли истинным выделенное ядро в отрицательных примерах. Простой проверкой убеждаемся, что оно везде ложно. Таким образом, причина улыбки человека найдена. Она возникает тогда и только тогда, когда встреченная им зверюшка имеет выгнутую вниз спину и две ноги.

