 полная версия
полная версияМоделирование рассуждений. Опыт анализа мыслительных актов

Рис. 29.
В роботизированных производствах используются роботы третьего поколения. Они должны быть достаточно автономны в своих действиях и уметь выполнять необходимый набор операций в динамически изменяющихся условиях производства. Это означает, что они не могут довольствоваться набором встроенных в них программ жесткого поведения. Интеллектуальный уровень таких роботов должен быть достаточно высоким. В их систему управления необходимо включить специальный блок – планировщик, задачей которого является составление программы действий робота в тех реальных условиях окружающей среды, которые в данный момент наблюдаются рецепторной системой робота. Для планирования целесообразной деятельности робот третьего поколения должен обладать определенными знаниями о свойствах окружающей среды и методах достижения целей в ней. Эти знания хранятся в его базе знаний, показанной в общей структуре робота на рис. 30. Глядя на этот рисунок, легко установить аналогии со схемой, показанной на предыдущем рисунке. В ЭВМ пятого поколения и в роботах третьего поколения осуществляется планирование будущей деятельности: автоматический синтез программы, выполняемый решателем, и программа деятельности, создаваемая планировщиком. Оба блока работают на основе знаний, хранящихся в базе знаний.
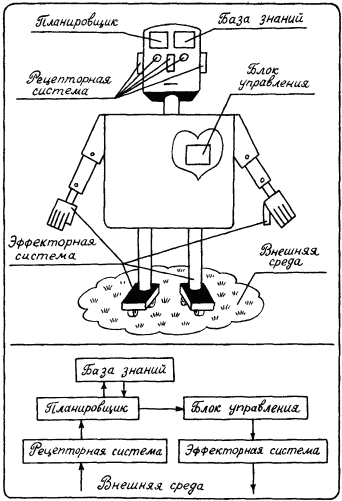
Рис. 30.
Экспертные системы, структура которых показана на рис. 31, также содержат базу знаний и логический блок, функции которого похожи на функции решателя и планировщика. Задача логического блока состоит в поиске вывода, ответа на входное сообщение, поступившее в систему. В базе знаний хранится необходимая информация о проблемной области, в которой работает пользователь. Его запросы поступают на профессиональном ограниченном естественном языке. В системе общения они преобразуются во внутреннее представление, с которым работает логический блок. Это внутреннее представление преобразуется в запрос к базе знаний. Если прямого ответа на запрос в базе нет, то логический блок осуществляет поиск косвенной информации, получаемой из хранящейся в базе с помощью достоверного или правдоподобного вывода. Система объяснения (это специфический блок, отличающий экспертные системы от других интеллектуальных систем) при необходимости по требованию пользователя поясняет ему, как получена та информация, которая выдана в качестве ответа.
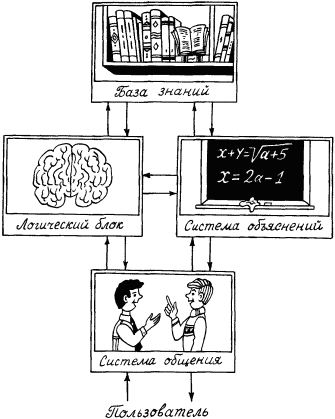
Рис. 31.
Мы хотим отметить, что ядром всех основных типов рассмотренных интеллектуальных систем являются база знаний и блок, осуществляющий вывод с помощью знаний (решатель, планировщик или логический блок). Этот вывод составляет основную процедуру, реализуемую в интеллектуальных системах.
Знания о внешнем мире могут иметь двоякую природу. Они могут содержать декларативное описание фактов и явлений внешнего мира, фиксирующее их наличие или отсутствие, а также основные связи и закономерности, в которые эти факты и явления входят. Но они могут содержать и процедурные описания того, как надо манипулировать с этими фактами и достигать целей, интересных для системы. Для описания знаний в интеллектуальных системах используются специальные языки описания знаний (ЯОЗ). Эти языки могут иметь различную природу. Нас будут интересовать (из-за темы данной книги) лишь языки логического типа. Простейшими видами таких ЯОЗ являются языки исчисления высказываний или исчисления предикатов вместе с теми процедурами вывода, которые для них известны. Однако в современных интеллектуальных системах такие языки используются довольно редко. Куда более распространены в них языки, основанные на продукциях. Продукции в общем виде можно записать в форме «Если…, то…». Сама по себе эта форма оказывается весьма характерной для фиксации знаний в различных областях человеческой деятельности. Вот несколько примеров текстов, взятых почти наугад из различных книг.
1. Если Академия заблагорассудит присоединить к себе ученого русского или иностранца, который не столько еще известен, чтобы мог требовать чести быть почетным членом, но своими полезными сочинениями или познаниями, или же ревностию и старанием, оказав полезные Академии услуги, обратил на себя отличное внимание, то она принимает его в корреспонденты, которые также разделяются на русских и иностранных. (Устав Санкт-Петербургской Академии наук 1836 года, № 85)
2. Если враг не сдается, то его уничтожают. Если кто к нам с мечем придет, то от меча и погибнет. (Высказывания полководцев.)
3. Если температура в верхней зоне превысит 75°, то необходимо открыть задвижку № 7. (Из инструкции.)
Число подобных примеров можно увеличивать до бесконечности. Они показывают, что представление фрагментов наших знаний о внешнем мире и действиях в нем в виде продукций имеет весьма большое распространение. Часть специалистов по интеллектуальным системам считает, что запись знаний в виде систем продукций носит универсальный характер – любые знания можно записать в такой форме. Они приводят немало примеров, когда знания, внешне не имеющие продукционной формы, удается перевести в систему продукций. Вот один из таких примеров.
Химические реакции мы со школьных лет привыкли воспринимать в форме соотношений следующего вида:
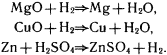
И т.д.
Покажем, как подобные утверждения можно записать в продукционной форме. Введем шесть сортов базовых элементов. К первому сорту отнесем металлы: Q1={Cu,Mg,Zn,…}. Ко второму – газы: Q2={H2,О,N,…}, к третьему – воду: Q3={H2O}. Четвертый сорт составляют окиси: Q4={MgO,CuО,…}. Пятый сорт образуют кислоты: Q5={H2SO4,HCl,…}. Наконец, шестой сорт образуют соли: Q6={ZnSO4,NaCl,…}. Зададим два базовых отображения. Первое отображает элементы из Q4 в элементы Q1. С его помощью для окисей выделяются основания. Второе отображение сопоставляет с именами веществ (под веществом будем понимать металл, газ, окись, воду, кислоту или соль) их химические формулы. Введем еще два оператора, которые будем использовать в продукциях: A(q) и E(q). Оператор A(q) добавляет в базу знаний q, а оператор E(q) убирает q из базы. Выпишем первый тип продукций для описания химических реакций.

Эта продукция годится для описания двух из приведенных выше химических реакций. Для описания третьей реакции используем другой тип продукций.

Вспомним программу «Логик-теоретик», которую мы обсуждали в третьей главе. Она была основана на том, что при доказательстве равенства двух выражений в исчислении высказываний использовалось понятие различия в двух выражениях и подбирались такие преобразования, которые эти различия устраняли. Для соотнесения различий с преобразованиями была построена таблица, в которой указывалось, какие преобразования какие различия устраняют. От этой таблицы чрезвычайно легко перейти к продукционной системе. Если i есть номер различия, a F* – одно из преобразований, то запись i
Два последних примера показывают, что продукциями являются не только те выражения, которые имеют форму «Если…, то…», но и многие другие выражения. К ним, по сути, сводятся все каузальные, т.е. причинно-cледственные утверждения, подобные тем, которые мы обсуждали в предшествующей главе. К ним же относятся и любые схемы вывода типа «посылки – следствие». Замкнутые системы правил типа законов короля Павзолия, описанных в романе Пьера Луиса «Приключения короля Павзолия»[9], также могут рассматриваться как особая форма продукций. Даже такие утверждения, как знаменитое «Если звезды зажигают, значит, это кому-то нужно» (В. Маяковский), можно рассматривать как продукцию.
Продукционные системы получили при представлении знаний в последнее время наибольшее распространение. Поэтому посвятим им специальный раздел нашей книги.
Продукционные системы
Анализ структур ЭВМ пятого поколения, роботов автономного типа и экспертных систем приводит к обобщенной структуре, показанной на рис. 32. Эта схема при условии, что система R представляет собой продукционную систему, может послужить основой для классификации типов продукций. На ней показано взаимодействие «рассуждающей» системы с внешним миром и базой знаний, из которой рассуждающая система может черпать накопленную ранее информацию о закономерностях этого мира и его состояниях. Из внешнего мира в рассуждающую систему приходит сиюминутная, текущая информация о наблюдаемых в этом мире фактах и явлениях. А из базы знаний поступает информация, имеющая более фундаментальное значение. Она может описывать законы внешнего мира, правила действий в нем, целевые структуры или ожидаемые отклики внешнего мира на те или иные воздействия на него. В памяти рассуждающей системы хранится текущая информация, связанная с ходом рассуждений. Со временем она либо исчезает, либо передается для хранения в базу знаний. Последнее происходит лишь в том случае, когда в процессе рассуждений появилась информация, которая может оказаться полезной для рассуждающей системы в будущем.

Рис. 32.
Теперь приступим к классификации продукций.
1. Продукции типа AW
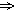
В качестве AW может выступать не только некоторое сообщение о W или некоторый факт, имеющий место во внешнем мире, но и прямое воздействие из внешнего мира на рассуждающую систему. Но что бы ни стояло в левой части продукции AB
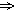
2. Продукции типа AW
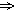
3. Продукции типа AK
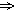
4. Продукции типа AR
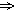
5. Продукции типа AK
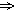
6. Продукции типа AW
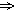
7. Продукции типа AR
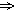
8. Продукции типа AR
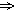
9. Продукции типа АК
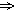
Сказанное наводит на мысль, что продукции могут иметь весьма различное значение. В качестве их левых и правых частей могут выступать и некоторые утверждения, и действия. Возможны не только те интерпретации, которые мы привели выше, но и ряд других. Например, продукции типа AW
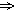
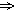
Продукционной системой будем называть любую совокупность продукций, в которую могут входить продукции любого из перечисленных выше типов.
Часто вместо продукций типа α
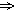
i, П, P, A
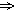
Здесь А
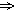
Элемент П характеризует сферу проблемной области базы знаний или предусловия применимости продукции. Эти предусловия ничем не отличаются от Р, но выделяют подсистемы продукций на ранг выше тех, которые выделяют условия. Предусловия задают формальную систему, в рамках которой будут проводиться логические рассуждения. Поясним эту мысль на примере. В обычном мире лошади не летают. Поэтому продукция «Если х лошадь, то она летать не может» в обычном мире всегда имеет место. Но если мы от обычного мира перейдем к миру греческих мифов, то продукция «Если лошадь есть Пегас, то она летает» станет верной. В мире же русской сказки продукция «Если лошадь есть Конек-Горбунок, то она летает» принимается без всякой критики. В приведенном примере предусловия П должны развести между собой обычный мир, мир греческих мифов и мир русской сказки.
Наконец, Q характеризует постусловия продукции, указывающие на те изменения, которые необходимо внести в базу знаний и в систему продукций после реализации данной продукции. Операторы A(q) и E(q), рассмотренные при описании химических реакций, являются примером таких постусловий.
Однако в общем виде продукции встречаются весьма редко. Предусловия характерны лишь для больших по объему и разнородных по составу баз данных и знаний, а постусловия – для планирующих систем роботов, когда используются продукции типа AR
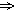
Если продукционная система такова, что на некотором шаге процесса может быть реализована не одна продукция, а несколько, то возникает ситуация, в которой необходимо уметь управлять ходом процесса. Эта ситуация настолько важна и принципиальна, что мы посвятим ее анализу специальный раздел. Именно в этом анализе раскрываются особенности использования продукций для моделирования рассуждений.
Управление выводом
Несколько изменим предшествующий рисунок. Будем считать, что информация из внешнего мира W поступает в базу знаний К, минуя рассуждающую систему R. Это позволит нам рассматривать лишь продукции типа АК
Последнее допущение позволяет ввести понятие состояния базы знаний в момент времени t, которое будем обозначать dt. Одно состояние может смениться другим по двум причинам. В момент t+1 из внешнего мира в базу знаний может прийти новая информация. Или в этот момент времени в базу знаний будет занесена новая информация, возникающая в результате срабатывания некоторой продукции.
Если в некоторый момент t состояние dt таково, что в нем удовлетворяются условия для некоторого множества продукций, то все они образуют фронт готовых продукций. Основная задача управления состоит в выборе из этого фронта очередной продукции для исполнения.
Для выбора важен вопрос о влиянии порядка выбора на окончательный результат рассуждений. Если имеются две продукции и ситуация такова, что изменение состояния базы знаний, которое может возникнуть при срабатывании одной из них, сказывается на выполнимости условий срабатывания для другой, то такие продукции естественно назвать зависимыми. Если две продукции независимы, то порядок их выбора из фронта не может сказаться на результате рассуждения. Поэтому интерес представляют лишь зависимые продукции.
Как осуществлять выбор в этом случае? Для пояснения складывающейся ситуации рассмотрим следующий пример. Только что кончилась лекция, наступил двухчасовой перерыв и группа студентов обсуждает проблему: куда сейчас пойти? В имеющихся условиях есть две альтернативы: пойти в кино (но никто не знает, какая там идет картина) или пойти в кафе-мороженое (но ни у кого нет уверенности, что кафе работает). Ясно лишь одно, что выбор одного варианта исключает выбор другого, так как кино и кафе-мороженое находятся в разных концах города. Убедившись, что кафе не работает, нет надежды успеть в кино, а обнаружив, что в кино ничего интересного не идет, нет надежды поесть мороженое. В условиях, когда никто из студентов не имеет никакой информации о кино и кафе, единственным разумным способом выбора является известное бросание монетки, т.е. случайный выбор. Но если в момент обсуждения появляется их сокурсник, который говорит, что только что был в кино и ушел, не досмотрев скучную картину (тем самым он меняет состояние «баз знаний» остальных студентов), то выбор активизируемой «продукции», соответствующей программе достижения кафе-мороженого, станет однозначным.
Описанная ситуация является в некотором смысле экстремальной. Один выбор исключает другой. Чаще это не так – после неудачного выбора можно вернуться к альтернативному выбору и попробовать другой вариант. Чтобы так можно было делать в процессах рассуждений, необходимо сохранять состояние базы знаний в момент выбора. Для реализации этого при принятии решения об альтернативном выборе можно, например, запоминать не всю информацию, имеющуюся в данный момент в базе знаний, а только ту ее часть, которая меняется в результате применения продукций из выбранного варианта. Если вариант окажется удачным, то новое состояние базы знаний будет сформировано на основе полученной в ходе проверки варианта информации. Если попытка окажется безрезультатной, то произойдет возвращение к состоянию базы знаний в момент выбора, а информация, полученная в ходе плохого варианта, сотрется из памяти. Практически все системы моделирования рассуждений в интеллектуальных системах используют этот прием, который называется «бэктрекинг».

