полная версия
полная версияКраткий курс «Общей семиотики»
Алгоритм системы зависит от типа используемых знаков: в случае с Рентгеном надо было построить аппарат для съемок с помощью х-лучей и определить, как лучше снимать те или иные вещи, уточнить длительность съемки и еще ряд технических подробностей. При применении законов гравитации Ньютона дело сводилось к простым подсчетам по выведенным им формулам. При сочинении стихов все теоретические установки по теории стихосложения остаются лишь благими рекомендациями для поэтов, которые опираются исключительно на свои способности и вкусы. Тем не менее, теория поэтики благополучно существует − в этом и проявляется разница между точными и неточными науками.
Следует заметить, что в ряде случаев результат манипуляций со знаковыми системами оказывается столь сложным, что для его расшифровки требуются специальные навыки. Так, сегодняшние данные анализов, производимых с использованием разных медицинских систем, иной раз остаются непонятными даже для врачей. Поэтому результат анализа подвергается расшифровке узкими специалистами и только после этого попадает на стол лечащего врача. Наконец, мы приходим к каким-то выводам и завершаем построение знаковой системы, но точку ставить еще рано.
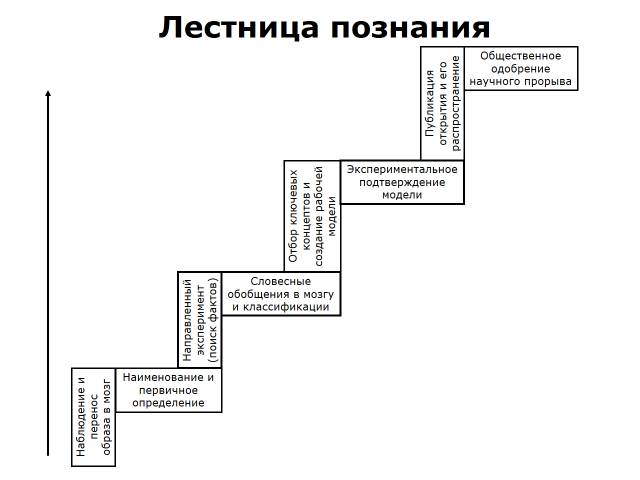
Проверка полученных результатовМы обязаны проверить, как функционирует система на практике. Контроль над системой начинается задолго до окончания работы над ее созданием. По этому критерию проверка разделяется на две категории: на пошаговую проверку наших посылок в процессе построения системы и на проверку эффективности системы в реальной действительности после окончания работы по ее созданию. Второй вариант проверки опять-таки подразделяется на две категории: немедленная проверка (обычно с участием независимых экспертов) и отложенная проверка с применением приборов и фиксацией бесперебойной работы нового продукта. Последний вид проверки может растянуться на многие годы. Все вышеизложенное по поводу создания знаковых систем я могу представить в виде диаграммы, которую я назвал «Лестницей познания» и помещаю здесь.
Логики манипулирования знаками в системах
Я различаю четыре вида логик действий при использовании знаковых систем. Покажу их на примерах пользования системой дорожных знаков:
1) Логика соответствия знаков с отображаемой онтологией. Допустим, мы ведем машину по незнакомой местности. Чтобы найти дорогу, мы используем дорожные знаки, а с другой стороны, все время обращаем внимание на реальные предметы вокруг и пытаемся объединить оба информационных ряда в один. Этим симбиозом мы, в конечном счете, и руководствуемся.
2) Логика формальная (логика мышления). Мы видим указатель, извещающий, что центр города находится там-то, и говорим себе: «Если нам указан путь в этом направлении и туда же мы должны попасть, то нам надо ехать в соответствии с указателем».
3) Логика знаковой системы. Подъезжая к центру, мы встречаемся с круговым объездом площади. Даже без всяких знаков мы пропускаем машины, объезжающие площадь, и лишь потом включаемся в транспортный поток. Сведения о таком поведении мы получаем не из дорожных знаков и не из формальной логики − они были выучены нами ранее при знакомстве с правилами дорожного движения.
4) Логика приложения всех прежде упомянутых видов. При подъезде к центру мы видим вскопанную территорию. Все перечисленные логики остаются в силе, но получают иное наполнение в связи с новым, непредвиденным фактором, который нам приходится учитывать. При этом нам самим приходится находить путь, зачастую с нарушениями правил вождения
Все четыре вида логик характерны для любых знаковых систем, за исключением так называемой «чистой математики» либо «художественного творчества». В них, в ряде случаев, не принимают во внимание логику соответствия. Так, из истории математики известны случаи, когда системы возникали просто под влиянием чисто математических выкладок без оглядки на возможность их практического применения. Примером может служить теория множеств, которая была впервые разработана Георгом Кантором в 1870 году. Он ввел понятие сравнения двух множеств, опирающееся на понятие их взаимно-однозначного соответствия:
«В теории Кантора понятие множества не определяется, а лишь поясняется на примерах (множество всех четных натуральных чисел, множество всех натуральных решений данного алгебраического уравнения и так далее). Множество считается заданным, если указано характеристическое свойство его элементов. Основное отношение − принадлежность одного множества другому. Общность понятия “множество” дала возможность применять его в любой математической области, и практически вся математика использует язык теории множеств. Однако самому Кантору шаг обобщения дался трудно, и его идеи были встречены современниками по-разному: Р. Дедекинд и Д. Гилберт признали особое значение теории множеств, в то время как Л. Кронекер был ее убежденным противником».21
Апологеты чистого искусства отрицают связь искусства с реальной действительностью и обращаются к абстрактной живописи, абстрактной музыке и пр. В этих случаях можно на полотно вылить банку краски и представить результат как нечто восхитительное и непревзойденное. Находятся и любители такого подхода. Но я пишу не о них, а о творцах, создающих нечто значительное не только для абстрактных изысков, но и для ежедневной жизни, улучшающейся за счет возникновения новых и новых знаковых систем.
Изменения, происходящие в знаках при их включении в знаковую системуВ этом пункте мы приходим к очень важному обобщению, которое вводит целый пласт моих рассуждений по поводу соотношения отдельного знака и того же знака в рамках какой-либо знаковой системы. Любой знак существует в двух ипостасях: как некая отдельная сущность и как компонент знаковой системы, причем две личины его существования радикально отличаются одна от другой. В первом случае знак выступает как нечто отвлеченное, как некий экспонат, готовый к реализации, но еще не получивший для этого необходимых ресурсов. В таком виде он представлен в разного рода номенклатурных списках, о которых я писал выше. В них он получает свое первоначальное имя и определение. Примерами таких списков для языковых систем могут служить толковые словари, для музыкальных систем − звуки октавы, для химии − таблица Менделеева, для медицинских систем − список всех болезней и недомоганий и пр.
Когда этот же знак вступает в какую-либо систему, он оснащается по-другому и приобретает специфические связи с иными членами той же системы.
Системная оснастка означает получение знаком иных значений, добавочных к тем, которые он имел в номенклатурных списках. Возьмем в качестве примера языковые системы знаков. Попадая в языковой контекст, слово становится не только тем, о чем было сказано в толковом словаре; оно еще становится «членом предложения» и приобретает массу дополнительных качеств, обязательных для выполнения функций той части речи, куда оно непременно попадает. Эти качества могут быть обозначены как синтаксическое и морфологическое оформление слова на выделенном ему месте в предложении. Кроме того, слово наделяется средствами связи с другими членами предложения.
Существительное в роли подлежащего наделяется связками со сказуемым-глаголом, со своим определением, выраженным прилагательным либо как-то иначе, и с другими членами предложения. Только оборудованное такими значениями слово может выполнять те задачи, которые на него накладывает «место службы». Специально для этого в систему закладываются значки, которые не имеют внесистемных значений, но обслуживают «значимые слова» в выполнении их роли в конкретном тексте: “как-то”, “во-первых”, “разумеется” и масса других подсобных слов. Все сказанное напоминает сценическое действо: действуют актеры, которые появляются в иных амплуа в разных пьесах. Каждый раз им приходится воплощать что-то другое, а для этого они прибегают к помощи обслуживающего персонала − от режиссера до работников сцены.
Приведу еще один пример − тригонометрию как знаковую систему, которая занимается определением различных величин с помощью треугольников. Это видно из самого названия системы: в названии “тригонометрия” соединены два греческих слова − “треугольник” и “измерять”. Понятие “треугольник” взято из онтологии; в нашем окружении мы сталкиваемся с треугольниками постоянно. Как пространственная фигура треугольник изучается в геометрии. Люди на практике обнаружили необходимость получения размеров разных частей треугольников, а их всего-то шесть − три угла и три стороны. Оказалось, что неизвестные части треугольника сравнительно легко вычислить с помощью остальных его частей, доступных для замера.
Так появились первые тригонометрические вычисления. В Древней Греции ими в основном пользовались для измерения дуг (частей окружности) через замер ограничивающей дугу хорды. Делалось это манипуляциями с вписанными в круг прямоугольными треугольниками. Такой же смысл приобрела эта часть математики в Древней Индии: «Замена хорд синусами стала главным достижением средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом в Индии было положено начало тригонометрии как учению о тригонометрических величинах».22
В конечном итоге мы получили полноценную знаковую систему с четким обозначением функций ее составных частей. Напомню только, что в прямоугольном треугольнике гипотенузой называется сторона, лежащая против прямого угла, а остальные стороны называются катетами. Еще надо знать, что в прямоугольном треугольнике два острых угла, один из которых выбирается в качестве аргумента, − именно по отношению к нему катет может быть прилежащим или противолежащим.
В тригонометрии насчитывается шесть функций:
Синус (sin) − отношение противолежащего катета к гипотенузе.
Косинус (cos) − отношение прилежащего катета к гипотенузе.
Тангенс (tan) − отношение противолежащего катета к прилежащему.
Котангенс (cot) − отношение прилежащего катета к противолежащему.
Секанс (scs) − отношение гипотенузы к прилежащему катету.
Косеканс (exscs) − отношение гипотенузы к противолежащему катету.
Имея в виду все названные концепты (я выделил их курсивом), мы можем сказать, что вне конкретных тригонометрических расчетов все выделенные концепты выполняют лишь номенклатурную задачу, − они дают имя и первичное определение (я их привел выше) своим референтам. Лишь в конкретных расчетах они получают жизнь. Только тогда мы наглядно выделяем их экзистенциальное наполнение, подбираем для них специальный алгоритм работы и подвергаем их математическим манипуляциям для получения нужного результата, Все это происходит с использованием соответствующих знаков.
Установление баланса между ведущими концептами знаковой системыКак же, все-таки, устанавливается баланс меж ду ведущими концептами той или иной знаковой системы? По моему разумению, это происходит следующим образом. Во-первых, отбирается центральный концепт, обычно именно он обозначает будущую знаковую систему. Для Менделеева задача заключалась в логически оправданном перечислении всех известных на тот момент времени химических элементов. Он записал все имена элементов на карточках и принялся их тасовать. Долгое время ничего не получалось, пока во сне ему не померещилось, что он нашел принцип расположения элементов в системе, даже два принципа − по возрастанию атомных весов (потом веса сменили атомные массы) и периодическому повторения качеств у некоторых элементов. Так появились «периоды», то есть разные группы системы, а вся схема была названа «периодической системой химических элементов». (Попрошу обратить внимание на появление во всем этом процессе разных групп описываемых вещей/явлений. Мы еще будем о них говорить.)
Затем устанавливаются те ведущие концепты, взаимодействие которых с центральным членом системы обеспечивает получение результата в манипуляциях со знаками. Они обычно называются «главными элементами» создающейся системы. Так, в предложении главными его членами называют подлежащее и сказуемое − именно связь между ними определяет тип предложения и его смысл. В физической картографии центральным элементом карты, т. е. «подлежащим», является то место или пространство, которое на ней обозначается, а «сказуемым» служат его географические координаты. После чего в это (уже знаковое пространство!) включаются все прочие знаки системы; для них специально обозначается вес в системе и связи с главными ее членами. Для библиографии книг в крупном хранилище книга или ее сородичи (манускрипты, журналы, газеты) выступают в роли центрального элемента системы, а сказуемым является местонахождение книги в данном хранилище.
Как было замечено, вокруг главных членов разворачиваются все их характеристики. Вокруг подлежащего концентрируются его определения, вокруг сказуемого − связанные с ним многочисленные члены предложения. И то, и другое самостоятельно сочетается со своими определениями, которых может оказаться очень много. Вне зависимости от количества определений главного члена предложения самым важным конструктивным их свойством является то обстоятельство, что они выступают в виде достаточно самостоятельных групп, что позволяет работать отдельно с каждой из них.
О выделении групп в знаковой системеВ языковых системах выделяются группа подлежащего и группа сказуемого. Они искусственно и на время изолируются, что позволяет работать с ними по отдельности. В алгебре теория групп выделяется в самостоятельный раздел и изучается по специальным алгоритмам. Наконец, в семиотике, предмете, который нас интересует, мы тоже выделяем отдельные группы знаков и их систем, и каждая специфическая группа знаков требует своих методов изучения. В конечном итоге группы собираются в единое целое, что не препятствует принципу отдельной обработки любой выделенной группы. Выше я говорил о написании Александром Ивановым картины «Явление Христа народу», упомянув о предварительных этюдах, которые создавались в течение многих лет. Существует даже специальная система создания крупных портретов, когда все полотно разбивается на отдельные клеточки, расписываемые последовательно. Потом они собираются в единый образ. Возьмите также в качестве примера решение какого-нибудь математического равенства; допустим, одна сложная дробь умножается на другую. Мы обрабатываем первый множитель, потом второй и, наконец, перемножаем их, получая конечный результат.
В любой сложной знаковой системе есть общий алгоритм действия, который составляется из последовательной обработки всех включенных в нее групп знаков, о чем в метаязыке системы всегда появляется подробное разъяснение.
Специфика знаковых значений на разных местах в изображаемом множествеОдин и тот же знак получает новые значения, появляясь на разных синтаксических местах в системе и, тем более, если он появляется в разных системах. Новые значения возникают у знака только после того, как он включается в систему и получает в ней свое особое место. В номенклатурном ряду разные значения указываются редко, если вообще упоминаются. В системе же они проявляются, прежде всего, в изменении соотношения роли знака и его веса в постоянно меняющемся состоянии системы. До начала шахматной партии мы применяем хорошо известные правила по количеству и месторасположению всех фигур. Мы знаем также примерный их вес: пешка принимается за единицу измерения, конь и слон признаются равными трем пешкам, ладья − пяти, а ферзь − всем восьми, если не более. В ходе партии соотношение все время изменяется − роль каждой фигуры начинает возрастать либо уменьшаться в зависимости от складывающейся ситуации на доске. Возникают иногда ситуации, в которых пешка получает более значимую роль, нежели ферзь. Майор или полковник − командиры высоких рангов в военной иерархии, но на службе в богом забытых местах это не играет значительной роли, ибо там просто невозможно реализовать потенциал высоких званий.
В некоторых системах один и тот же знак специально наделяется разными значениями, которые легко определить. Такая ситуация наблюдается, например, в позиционной системе счисления в арифметике. В ней всего 10 знаков в каждой позиции, но они изменяют значения используемых в них знаков в зависимости от их конкретной позиции. В первой позиции они означают единицы, в следующей − десятки, далее − сотни, тысячи и т.д. до бесконечности, давая возможность легкой записи любого числа с помощью всего десяти знаков. Эта их особенность предоставляет нам шанс использовать простые алгоритмы для всех арифметических действий, пользуясь их позиционными свойствами, например, при сложении или умножении в столбик и др.
Таким же свойством обладают буквы в алфавите. С помощью 33 букв русского алфавита можно записать неисчислимое количество слов, которые мы употребляем. Происходит это потому, что мы записываем звуки устной речи, которых оказывается совсем немного. Таким образом мы успешно отказались от сложнейших систем языковых записей, существовавших ранее и сохранившихся еще и сегодня в некоторых языках (рисуночных, иероглифических, клинописных и пр.).
Есть еще один важный критерий изменения значения знаков по мере их вхождения в знаковую систему: вначале они получают синтаксические значения, приобретая персональное синтаксическое место, а потом уже наделяются соответствующими морфологическими добавками. Обратимся снова к языковым знакам. Слова получают имя и определение еще в номенклатурных системах (например, в толковых словарях). Будучи помещены в какой-то текст, они приобретают дополнительные значения в соответствии с грамматикой соответствующего языка. Я писал об этом выше, в разделе «Изменения, происходящие в знаках при их включении в знаковую систему».
Здесь я хочу еще раз подчеркнуть, что наделение системными значениями проходит по указанному маршруту: вначале слова наделяются синтаксическими значениями и только потом они получают соответствующие их синтаксическому положению морфологические добавки. Важно отметить, что их синтаксический статус определяет еще и их место в предложении; скажем, прилагательные в роли определения в русском языке ставятся перед определяемыми, а в иврите после определяемых слов. Во французском языке некоторые прилагательные ставятся после, а некоторые перед определяемыми словами, и эти случаи приходится специально заучивать.
То же самое происходит в иных, а не только в языковых системах, но процесс этот детально изучен только в грамматиках того или иного языка, и поэтому я пользуюсь здесь лингвистической терминологией. Я вообще предлагаю сохранить ее для любых знаковых систем. Так, например, в картографии, где базисным знаком является имидж (образ), а не слова, принятые в языковых системах, понятие синтаксиса может относиться к сетке координат и к четырем сторонам света, в системе которых располагаются все остальные знаки. Интересно посмотреть, как исторически люди пришли к изображению географических знаков.
Образ − это такой знак, который пытается сохранить подобие с тем, что он изображает, в то время как слова в огромном большинстве случаев такого подобия в себе не содержат. Это меняет расстановку и понимание смыслов в картографических системах по сравнению с системами языковыми. В истории картографии люди поначалу пытались отразить подобие того, что они видели воочию в жизни, рисунками, помещенными на картах. Еще в XVIII веке Джонатан Свифт писал:
«Географы в Африке вместо белых пятен рисовали дикарей, а в незаселенных местах вместо поселений изображали слонов».23
Очень скоро картографы убедились, что рисунки не годятся для подлинной картографии, и перешли на символический показ онтологических сущностей географии и на их математическую обработку, чтобы хоть как-то сохранить подлинные очертания реальных контуров суши и водных пространств. Все началось с наложения сетки координат, которая покрывала бы всю Землю и показывала ее шарообразность. В образовывавшиеся квадраты пытались втиснуть участки суши, которые умещались в отведенных для них местах с необходимыми для этого поправками по соответствующим математическим проекциям. Применение картографической сетки и появившихся конвенциональных знаков является внедрением синтаксических основ в картографические знаковые системы. Отныне в квадратах на картах можно было помещать целые наборы знаков тех реальных объектов, которые фактически находились на территории квадрата. Так картография очертила основу своих знаков и заключенных в них значений для географических изображений (сначала синтаксических, а потом и морфологических).
Классификация систем по охвату изображаемого феноменаПо данному параметру можно разделить знаковые системы на три категории: на главную систему, ее регистры и вторичные системы.
Допустим, в классической музыке можно выделить несколько жанров, как-то: симфонию, сонату, этюд и пр. Каждый жанр строится по своим правилам, которые определяют его композицию. Это − главная система данного жанра. Она получает выражение в разных регистрах. При исполнении симфонии каждая группа инструментов получает свой вариант системы: смычковые играют по своим нотам, духовые − по своим и т.д. Забота дирижера − свести их вместе в едином русле главной системы. Если оркестр представляет оперу или дополняется хором, то вступают в строй дополнительные для данного жанра системы: пения, драматического исполнения партии, декораций и пр. Я назвал их вторичными. В конечном итоге получается единое целое, производящее соответствующее впечатление на публику.
Я хотел бы добавить еще один пример регистров в системах. Азбука Морзе, используемая на телеграфе и для перестукивания в тюрьме, демонстрирует два разных регистра одной системы, причем они отличаются друг от друга. Так что регистры должны быть приспособлены для использования системы в изменившихся условиях их применения. .
Еще один пример. В системах ориентации на местности различаются системы ориентации на суше, на море и в воздухе. Каждая формулирует свои правила поведения, которые изучаются, охватывая полную сферу данного вида. Регистры главной системы включают отдельные правила поведения ведущего группы, его помощников, санитаров и прочих лиц разного назначения. У каждого из них есть свои специфические функции и знаки для их исполнения: одни прокладывают дальнейший путь, другие ведут группу, третьи дешифруют следы и пр.
Вторичные системы дают варианты навигации для конкретных условий ее проведения: ночью, с преодолением возможных препятствий, передвижение с переносом тяжелых предметов и пр. Так это происходит в любых системах, достаточно сложных по своей конструкции.
Классификация систем по их конструкцииПо этому параметру я различаю линейно построенные системы знаков, системы периодического построения и смешанные системы, в которых присутствуют знаки различного семиотического наполнения.
Линейно построенные системы превалируют в номенклатурных списках. Списки значительно отличаются как по размерам, так и по способам их составления. Например, список слов того или иного языка практически бесконечен и движется в одном направлении − в сторону его постоянного увеличения. А натуральный ряд чисел тоже бесконечен, но он может развиваться в двух направлениях, как в сторону увеличения вправо от нуля, так и в сторону отрицательных значений. Допустим, хронология постоянно пополняется по мере нарастания лет для того или иного события, но может дополняться фактами вглубь давно прошедшего времени.
Это − огромные знаковые системы, значение которых для цивилизации невозможно переоценить. Существуют линейно построенные знаковые системы малого объема − они работают в пределах, которые нам достаточны для сиюминутных нужд. Например, термометр представляет диапазон температур человеческого тела, а он весьма невелик. Термометр тоже имеет два направления температур, но исходной точкой отсчета выступает не ноль, а температура от 35о С до 37о С. Эта температура принята как нормальная; вправо от нее уходят показатели повышенной температуры, влево − пониженной.
Номенклатуры могут быть как открытыми для введения новых знаков, например, список имеющихся в магазине товаров, так и закрытыми, изменения в которые вносятся по специальному решению органов, на это уполномоченных. Существует множество списков, составляемых ad hoc, скажем, список спортсменов, допущенных к соревнованиям. Кончаются соревнования − списки теряют свою значимость. Есть еще один параметр конструирования подобных списков − их составление по какому-то специфически выбранному принципу. Чаще всего по алфавиту: список телефонных абонентов какой-то местности, запись фамилий учащихся в классном журнале и пр. А вот списки исторических событий или личностей составляются по хронологии появления указанных в них событий или лиц.