Рефлексивные процессы и управление. Сборник материалов XI Международного симпозиума 16-17 октября 2017 г., Москва

Литература

1. Birshtein, B., Borsevici, V. (2002). Stratagems of Reflexive Control in Western and Oriental Cultures. International Interdisciplinary Scientific and Practical Journal ―Reflexive Processes and Control‖, vol 1, nr. 2. Moscow: "Kogito Center" Publishing House

2. Lepskiy, V.E. (2010) Reflexive and Active Environments of Innovative Development. – Moscow: "Kogito Center" Publishing House

В. В. Карюкин, Ф. С. Чаусов (Военный учебно-научный центр «Военно-Морская Академия», Санкт-Петербург) Рефлексивные игры противодействия

Аннотация. Рассматриваются рефлексивные игры при наличии признаков распознавания.

Ключевые слова: рефлексивные игры противодействия, признаки распознавания.

V. V. Karjukin, F. S. Chausov (Military educational and scientific center «Naval Academy»,St. Petersburg)

REFLEXIVE GAMES COUNTER

Abstract. Reflexivity games if there are signs of recognition.

Keywords: reflexive games, signs of recognition.

Задачи противодействия, рассматриваемые нами [1–3], характеризуются тем, что сначала делает выбор один из игроков, а второй игрок, чтобы не быть обреченным на поражение, должен разгадать выбор противника. Таковы, например, игра «нападение и оборона»[1], «игра в прятки»[4]. Изучение таких игр требует привлечения признаков распознавания стратегии противника. Данная задача требует привлечения теории рефлексивных игр [4].

Необходимые определения и обозначения. Рассмотрим игру, задаваемую матрицами:

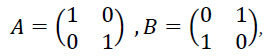
где первая матрица есть матрица выигрышей игрока 𝒜, а вторая дает выигрыши игрока ℬ. Игрок 𝒜 выбирает строчку (𝑖 ∈ 1,2), игрок ℬ – столбец (𝑗 ∈ 1,2). После того как выбор сделан, игрок 𝒜 получает выигрыш 𝑎𝑖𝑗, а игрок ℬ – выигрыш 𝑏𝑖𝑗. Матрицы известны обоим игрокам. Данная игра является игрой с постоянной суммой 𝑎𝑖𝑗 + 𝑏𝑖𝑗 = 1, и ее равновесные смешанные стратегии одинаковы для обоих игроков

. Здесь введены обозначения: 𝑥1, 𝑥2– вероятности с которыми игрок 𝒜 выбирает первую (𝐴1) или вторую (𝐴2) стратегию (первую или вторую строчку матрицы 𝐴); аналогично (𝑦1𝑦2) – распределение вероятностей на стратегиях 𝐵1,𝐵2 (столбцах матрицы 𝐵). Математическое ожидание выигрыша для игрока 𝒜 равно 0.5. Дополним описание данной игры допущением, что для каждой стратегии игроков известны признаки распознавания, известные обоим. Кроме того, для каждого такого признака существуют косвенные признаки, некоторые из которых носят рефлексивный характер. Будем считать, что скрытие косвенных признаков невозможно.

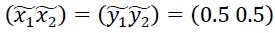
Приведем определения для признаков распознавания. Введем обобщенное обозначение S для некоторой стратегии игрока.

Признак α называется необходимым признаком для распознавания стратегии, если он принимает значение истина всякий раз, когда реализуется распознаваемая стратегия. В символах математической логики это отображается импликацией S → а и правилом вывода (распознавания) S,S → α/α: если противник выбрал стратегию S, то должен наблюдаться признак α.

Признак β называется достаточным признаком для распознавания стратегии, если из факта наблюдения признака β(логическая формула признака приняла значение истина) следует выбор стратегии S. В символах математической логики это отображается импликацией β → S и правилом вывода (распознавания) β/β → S/S: если наблюдается признак β, то противник выбрал стратегию S.

Признак γ является необходимым и достаточным для распознавания стратегии S, если утверждения γ и S одновременно истинны или одновременно ложны. С прикладной точки зрения наблюдение признака γ позволяет делать безошибочный прогноз о выборе противника.

Из факта наблюдения признака α не следует достоверное заключение о выборе стратегии. Следует лишь возможность реализации распознаваемой стратегии S, поскольку множество истинности признака а шире, чем множество истинности необходимого и достаточного признака у. Однако, из факта ложности признака α (наблюдается ā) следует, что стратегия S не будет реализована. Действительно, это следует из закона логики (S → а) → (а → S). Из факта отсутствия признака β не следует, что стратегия S не будет реализована, поскольку множество истинности достаточного признака уже, чем множество истинности признака γ.

Для игры 2×2, описанной выше, из изложенного следует: 1) если γ необходимый и достаточный признак для S, то γ есть необходимый и достаточный признак для; 2) если а необходимый признак для S, то ā есть достаточный признак для S¯; 3) Если β достаточный признак для S, то β¯ есть необходимый признак для S¯.

Пусть игра, описанная выше, такова что, игрок 𝒜 для распознавания стратегий противника использует разные признаки: для В1 использует некоторый признак δ1, а признак δ2 – для стратегии В2. Допустим, что данные признаки приводят к успешному распознаванию с одинаковой вероятностью θ. Использование признаков увеличивает математическое ожидание выигрыша, если вероятность θ > 0.5.

Если в игре 2×2: 1) игрок 𝒜 для распознавания стратегии В1 использует только необходимый признак а1; 2) достаточный признак α2 реализуется в разных ситуациях с вероятностью θ; 3) вместе признаки дают необходимый и достаточный признак; 4) для распознавания стратегии В2 используется признак α1¯. Тогда: 1) если игрок ℬ использует равновесную стратегию, то математическое ожидание 𝜈𝒜 выигрыша игрока 𝒜 равно

, в этом случае вероятность выигрыша игрока 𝒜 больше равновесного при любом θ; 2) для любых смешанных стратегий игрока ℬ имеет место 𝜈𝒜 ∈ [𝜃; 1], и величина 𝜈𝒜 больше равновесного выигрыша при θ > 1/2. Следовательно, использование необходимого признака дает выигрыш больший, чем равновесный выигрыш 0.5 при θ > 0.5 для любых стратегий (у1; у2).

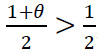
Если игроку 𝒜 известны оба необходимых признака: α1 – для стратегии В1 и признак β1 для В2 (𝛼1𝛽1 = 0), то он делает безошибочный прогноз при любом выборе противника.

При распознавании стратегии противника, игрок может обнаружить несоответствие между признаком, установленным ранее, и признаком, наблюдаемым в данный момент. Это может быть обусловлено следующими причинами: ошибками распознавания; управляющим воздействием противника, который демонстрирует противоположные значения некоторых элементарных признаков; неполнотой признака, если признак достаточный.

Устранить эту неопределенность, методами математической логики можно лишь при привлечении рефлексивных соображений [5], базирующихся на знании данной предметной области и(или) психологическом портрете противника.

Большое значение в принятии решения, основанном на использования признаков, дает уверенность в достоверности используемых признаков. Пусть признак K в результате n разыгрываний данной игры приводил к правильному распознаванию стратегии. Насколько можно быть уверенным в том, что в текущем разыгрывании данный признак приведет к успешному распознаванию. Другими словами, не является ли это игрой случая. Перед нами задача математической статистики, в которой нулевая гипотеза утверждает, что мы имеем дело со схемой независимых испытаний и наблюдаемые результаты носят случайный характер. Альтернативная гипотеза заключается в том, что из истинности данного признака K всегда следует правильное заключение. Определим достоверность признака как нижнюю границу вероятности того, что в следующем разыгрывании игры вероятность успешного распознавания выше, чем вероятность ошибки. Заметим, что достоверность характеризует следование: K ⟹ S, а не сам признак. Данная оценка вероятности равна:

. Для утверждения, носящего рефлексивный характер и вводимого в рассмотрение впервые, достоверность естественно положить равной 0.5. Если рассматривается цепочка таких рефлексивных следований длины p, то ее достоверность равна 0.5p. Это, в частности, относится к рефлексивным рассуждениям, основанным на определении ранга рефлексии в конечных играх [4]. Однако, если ранг рефлексии установлен в результате длительных наблюдений за противником, то его значение также является признаком, который позволяет сделать правильный выбор. Все это говорит о необходимости включения рефлексивных рассуждений в теорию игр.

Литература

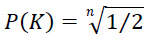
1. Карюкин В. В., Чаусов Ф. С. Ретроспективный рефлексивный логический анализ Нормандской десантной операции(6 июня 1944 г.). «Рефлексивные процессы и управление», 2017, в печати.

2. Карюкин В. В., Чаусов Ф. С. Математическая модель распознавания ранга рефлексии в ситуациях противодействия противнику. «Математическое моделирование», в печати.

3. Чаусов Ф. С. Рефлексивный подход в управленческой деятельности. – СПб.: СПбВМИ, 2008, 286 с.

4. Новиков Д.А, Чхартишвили А. Г.Рефлексивные игры. – М., СИНТЕГ, 2003, 203 с.

5. Лепский В. Е. Технологии управления в информационных войнах (от классики к постнеклассике) – М.: «Когито-Центр», 2016. – 160 с. http://www.reflexion.ru/Library/Lepskiy2016a.pdf

Е. Н. Князева (Национальный исследовательский университет «Высшая школа экономики», г. Москва)

Биосемиотика Я. фон Икскюля как методологическая основа конструирования рефлексивно-активных сред

Аннотация. Основатель биосемиотики Я. фон Икскюль активно повлиял на развитие когнитивной науки и философии сознания и является ныне высоко цитируемым и популярным автором. Не только люди, но и животные живут в знаковой реальности. Их окружающая среда активна. Это мир смыслов— Umwelt, который активно строится живым существом и строит его самого.

Ключевые слова: рефлексивно-активная среда, биосемиотика, конструктивизм, функциональный круг, Якоб фон Икскюль.

H. N. Knyazeva (National Research University Higher School of Economics, Moscow)

J. VON UEXKÜLL‘S BIOSEMIOTICS AS A METHODOLOGICAL BASIS OF CONSTRUCTION OF REFLEXIVE-ACTIVE MEDIA

Abstract. The founder of biosemiotics J. von Uexküll actively influenced the development of modern cognitive science and philosophy of mind and is nowadays a highly cited and popular author. Not only humans, but also animals live in the world of signs and meanings. Their environment is active. This is a world of meanings Umwelt, which is actively built by a living being and builds it itself.

Keywords: reflexive-active medium, biosemiotics, constructivism, functional circle, Jakob von Uexküll.

Введенное биологом-теоретиком Якобом фон Икскюлем (1864–1944) уже более 100 лет назад понятие Umwelt, стало центральным в биосемиотике, начало развитию которой как междисциплинарному направлению исследований было положено этим ученым. Umwelt – это не просто окружающая среда организма, это не просто энвайронмент. Понятие Umwelt содержит в себе глубокие мировоззренческие смыслы и несет в себе мощный методологический заряд. Оно оказалось действенным не только внутри теоретической биологии и экологии (кстати, и сама экология сегодня может пониматься в расширенном виде, вплоть до экологической философии), попав в сопряжение с понятием экологической ниши, но и для развития кибернетики, общей теории систем, теории управления, обнаружив свою эвристичность для развития понятий отрицательной обратной связи, гомеостазиса

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.