Настольная игра «Футбол на бумаге»

S=2+2+…+2=Ч+Ч+…+Ч=Ч

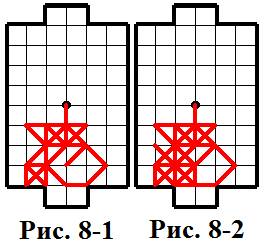
На рисунке 8-1 приведён пример конструкции. Из данного положения ходят Нижние ворота (Н), хотя для них нет выхода, они «чудесным образом» его находят, и проход к воротам с лёгкостью перекрывается (рис. 8-2). Дело в том, что Нижние ворота (Н) попросту «смухлевали». Из пересечений d3 и c4 исходит нечётное количество рёбер. Этого быть никак не может, т.к. в соответствии с доказанным выше утверждением из пересечений d3 и c4 должно исходить чётное количество рёбер. Нижние ворота (Н) просто-напросто дорисовали «недостающее» ребро (c4;d3), через которое им забивается гол!

5). Дано: симметричное футбольное поле произвольных размеров.

Дать определение: понятия чётных и нечётных пересечений.

5.1. В ФУТБОЛЕ НА БУМАГЕ существует два вида пересечений: тупиковые и нетупиковые.

Тупиковыми называются пересечения, в которых можно попасть в тупик. Соответственно нетупиковыми называются пересечения, в которых нельзя попасть в тупик.

Попасть в тупик можно, если почти все рёбра, исходящие из данного пересечения заняты, т.е. если у данного пересечения осталось только одно незанятое ребро. Пример такого пересечения показан на рисунке 9.

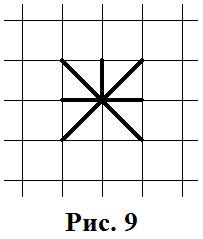
Занявший такое пересечение игрок попадает в «тупик» и по правилам ФУТБОЛА НА БУМАГЕ проигрывает (рис. 10).

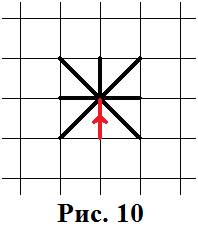
Нельзя попасть в «тупик» если у данного пересечения осталось два незанятых ребра. Пример такого пересечения показан на рисунке 11.

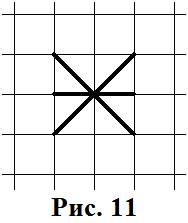
Занявший такое пересечение игрок по правилам ФУТБОЛА НА БУМАГЕ должен продолжить ход. Т.о. больше нет возможности сходить в это пересечение, т.к. все исходящие из него рёбра заняты (рис. 12).

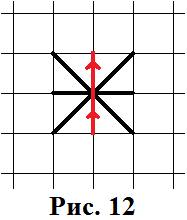
Т.о. можно условно обозначить тупиковые пересечения – нечётными, а нетупиковые – чётными.

5.2. Теперь давайте исследуем на чётность все виды пересечений футбольного поля (кроме воротных пересечений – они этим свойством не обладают, т.к. по правилам ФУТБОЛ НА БУМАГЕ, если такое пересечение занято – одна из сторон автоматически проигрывает партию; это особенные пересечения).

В ФУТБОЛЕ НА БУМАГЕ существует семь видов пересечений (они показаны на рисунке 13).

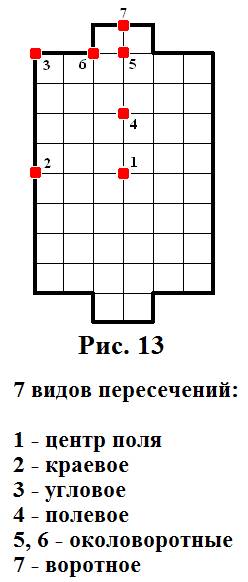
Исследование на чётность:

1 – центр поля (d6):

Из этого пересечения делается первый ход, после чего от него отходят семь незанятых граней (рис. 14).

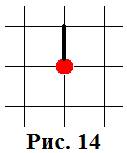
При дальнейшей игре, заняв центр, нужно от него «оттолкнуться», т.е. каждый раз будут заниматься две грани: 7:2=2×3+1

Т.е. после трёх прохождений через центр от него будет отходить одна незанятая грань. Если эту грань занять – ты попадёшь в тупик. Таким образом, центр – это нечётное пересечение.

2 – краевые пересечения (a3-…-a9; g3-…-g9; b2; b10; f2; f10):

Поскольку эти пересечения с самого начала игры считаются занятыми, то, сходив в одно из таких пересечений, от него надо «оттолкнуться». После этого от данного пересечения отходит одна грань (рис. 15).

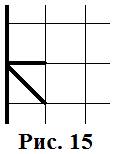
Заняв эту грань – ты попадёшь в тупик. Таким образом, краевые пересечения являются нечётными.

3 – угловые пересечения (a2; g2; a10; g10):

Очевидно, что данные пересечения являются нечётными, поскольку от них отходит всего одна грань, заняв которую ты попадаешь в тупик.

4 – полевые пересечения ((b3-…b9;…; f3-…f9) – кроме d6):

Эти пересечения в начале партии являются пустыми и по ходу игры «превращаются» в занятые. Это происходит следующим образом: одна из сторон занимает полевое пересечение и в нём «останавливается», затем другая сторона ходит из этого пересечения. Т.о. от полевого пересечения будут отходить шесть незанятых граней (рис. 16):

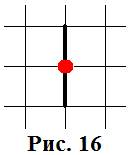
При дальнейшей игре, заняв полевое пересечение, нужно от него «оттолкнуться», т.е. каждый раз будут заниматься две грани: 6:2=2×3

Т.е. после трёх прохождений через полевое пересечение ты займёшь все грани и дальнейший проход в такое пересечение невозможен. То есть, в полевом пересечении нельзя попасть в тупик, оно является чётным.

5, 6 – околоворотные пересечения (c2; c10; e2; e10; d2; d10):

Часть рёбер, исходящих от данных пересечений, соединена с воротными пересечениями, т.е. с пересечениями, заняв которые одной из сторон автоматически засчитывается поражение. Таким образом, условие тупиковости (нечётности) для околоворотных пересечений не может быть выполнено и они являются чётными.

Если бы в ФУТБОЛЕ НА БУМАГЕ отсутствовало правило гола – то 6 пересечения (c2;c10;e2;e10) превратились бы в тупиковые (поскольку от них отходят пять незанятых граней), а 5 пересечения (d2;d10) остались бы также чётными и были бы простыми полевыми пересечениями.

Теперь давай представим результаты в графическом виде (нечётные и воротные пересечения изображены красным цветом, чётные – чёрным):

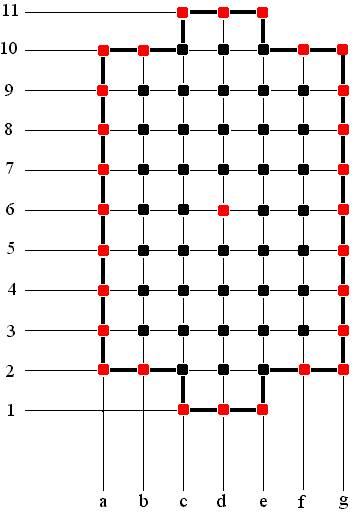
Таким образом, если партия ведётся строго по правилам и доигрывается до победного конца – последним занимается одно из красных пересечений.

6). Следствие нечётности пересечений:

а). Введём определение изолированной группы:

изолированная группа – это конструкция, при которой проход к обоим воротам полностью перекрыт. Пример изолированной группы показан на рисунке 17.

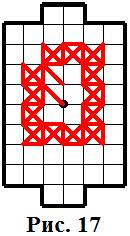
б). Внутри изолированной группы всегда есть хотя бы одно нечётное пересечение. Это вполне очевидно – ведь если проход к обоим воротам полностью перекрыт, то в итоге одна из сторон попадёт в тупик, т.е. займёт тупиковое (нечётное) пересечение.

В примере представленном на рисунке 17 таким пересечением является центр.

Дано: симметричное футбольное поле произвольного размера

Доказать: на данном поле нельзя построить конструкцию следующего вида:

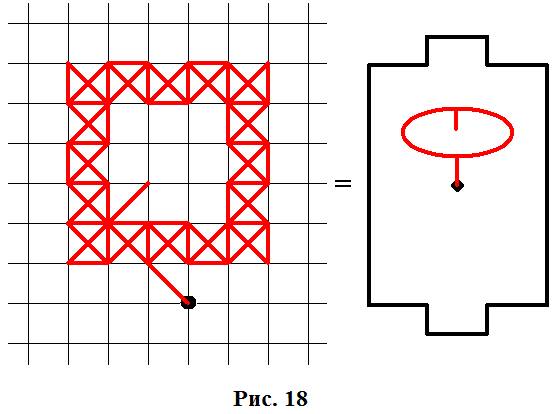
Доказательство: допустим, что такую конструкцию можно построить, тогда внутри неё должно быть хотя бы одно нечётное пересечение, но таких пересечений внутри данной конструкции нет, а есть только полевые пересечения, которые являются чётными, в чётном пересечении нельзя попасть в тупик. Мы пришли к противоречию – следовательно, такую конструкцию нельзя построить, если строго соблюдать правила ФУТБОЛА НА БУМАГЕ. Приведённая на рисунке 18 конструкция построена с нарушением правил игры.

Данное утверждение справедливо для футбольных полей любых конфигураций, необходимо только, чтобы совпадала «внутренняя геометрия».

7). Дано: ты договариваешься с противником о проведении матча.

Определить: на каком количестве партий в матче тебе нужно настаивать, чтобы твои шансы на успех были максимальными.

Решение:

Матч может состоять из нечётного или чётного количества партий. Поскольку в отдельной футбольной партии ничьи быть не может, то в нечётном матче всегда определяется победитель. В матче же, состоящем из чётного количества партий игроки могут сыграть в ничью. Для победы в матче требуется выиграть абсолютное большинство партий:

- для нечётного матча – k партий из n, где (n+1)/2 k n;

- для чётного матча – f партий из m, где m/2+1 f m

Введём несколько понятий:

– нечётный матч – матч, состоящий из нечётного количества партий.

- чётный матч – матч, состоящий из чётного количества партий.

Определение «формулы» матча зависит от нескольких обстоятельств:

1). Тебе нужна победа в матче или тебя устроит и ничья (т.е. игра будет вестись на победу или на непоражение); т.к. выиграть матч, состоящий из нечётного количества партий N, меньше шансов, чем не проиграть матч, состоящий из чётного количества партий (N+1).

Для наглядности можно привести простой пример:

Перед тобой дилемма – выбирать матч, состоящий из одной или из двух партий. Очевидно, что более надёжный вариант – это две партии, поскольку даже если ты проиграешь в первой партии – возможно тебе удастся отыграться во второй и свести матч вничью. Но, если тебе в силу тех или иных обстоятельств нужна только победа, конечно лучше играть одну партию. Таким образом, здесь всё зависит от твоей цели.

2). Знаешь ли ты свои шансы на победу в одной партии.

3). Если знаешь то каковы они (меньше или больше, чем у противника, или равны).

1. Допустим, что ты знаешь свои шансы на победу в отдельной партии:

- Н1(n) – вероятность не проиграть в матче, состоящем из n партий, для первого игрока

- Н2(n) – вероятность не проиграть в матче, состоящем из n партий, для второго игрока

- В1(n) – вероятность выиграть в матче, состоящем из n партий, для первого игрока

- В2(n) – вероятность выиграть в матче, состоящем из n партий, для второго игрока

- Д(n) – вероятность того, что игроки сыграют в ничью матч из n партий (n – всегда чётное)

1.1. Вероятность того, что матч выиграет один из игроков или он закончится в ничью (если это чётный матч) равна 1. Пускай в нашем небольшом исследовании 1 будет равна 729 (36) шансам.

Допустим, что: Н1(1)=В1(1)=1/3; тогда Н2(1)=В2(1)=2/3. Т.е. вероятность выиграть для первого игрока в одной партии равна 243 шансам, для второго – 486 шансам. Тогда:

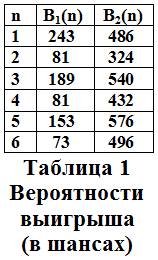
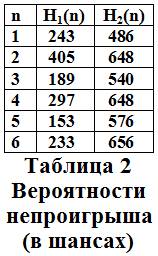
Выводы из таблиц 1 и 2:

1). Шансов выиграть в нечётном матче из n партий больше, чем в чётном из (n+1) партий;

2). Шансы на выигрыш у более слабого игрока с увеличением количества партий «тают на глазах», а у более сильного игрока наоборот возрастают;

3). Шансов не проиграть в чётном матче из n партий больше, чем в нечётном из (n-1) партий;

4). Шансы на непроигрыш у более слабого игрока с увеличением количества партий также становятся меньше, а у более сильного игрока возрастают.

1.2. Допустим, что: Н1(1)=В1(1)=Н2(1)=В2(1)=1/2. Т.е. шансы игроков на выигрыш в отдельной партии равны.

1.2.1. Для нечётного матча (n – нечётное число):

1=В1(n)+В2(n), т.к. В1(1)=В2(1), тогда и В1(n)=В2(n)=1/2; т.е. вероятность выиграть у каждого из игроков в нечётном матче постоянна и равна 1/2.

1.2.2. Для чётного матча (n – чётное число):

1= В1(n)+В2(n)+Д(n), т.к. В1(1)=В2(1), тогда и В1(n)=В2(n)=Х

1=Х+Х+Д(n)=2Х+Д(n)

2Х=1-Д(n)

Х=(1-Д(n))/2=1/2-Д(n)/2

Х<1/2

В1(n),В2(n)<1/2; т.е. вероятность выиграть у каждого из игроков в чётном матче меньше 1/2.

Х+Д(n)=1-Х, т.к. Х<1/2, то Х+Д(n)>1/2; т.е. вероятность не проиграть у каждого из игроков в чётном матче больше 1/2.

Однако вероятности выигрыша и непроигрыша непостоянны. Вероятность сыграть в ничью с увеличением количества партий уменьшается, следовательно, вероятность выигрыша увеличивается, а непроигрыша уменьшается. Обе эти величины стремятся к 1/2. Т.е. больше всего шансов не проиграть у игроков в матче из двух партий:

Н1(2)= Н2(2)=3/4

2. Допустим, что ты не знаешь свои шансы на победу в отдельной партии:

2.1. Если хочешь играть на победу – тебе нужен нечётный матч, состоящий из как можно меньшего количества партий. Оптимальный вариант – матч из одной партии. Объясняется это очень просто: т.к. ты не знаешь своих шансов, то они могут оказаться меньше, чем у противника, и, выбирая «длинный» матч, ты только усугубишь своё положение. Если же твои шансы больше или равны – то они такими и останутся.

2.2. Если хочешь играть на непоражение – тебе нужен чётный матч, состоящий из как можно меньшего количества партий. Оптимальный вариант – матч из двух партий.

Теперь можно подвести общий итог:

1). Если хочешь не проиграть – тебе нужен чётный матч:

1.1. Если знаешь свои шансы:

1.1.1. Играешь сильнее – чем больше партий, тем лучше.

1.1.2. Играешь слабее или на равных – чем меньше партий, тем лучше. Оптимальный вариант – матч из двух партий.

1.2. Если не знаешь свои шансы – чем меньше партий, тем лучше. Оптимальный вариант – матч из двух партий.

2). Если хочешь выиграть – тебе нужен нечётный матч:

1.1. Если знаешь свои шансы:

1.1.1. Играешь сильнее – чем больше партий, тем лучше.

1.1.2. Играешь слабее – чем меньше партий, тем лучше. Оптимальный вариант – матч из одной партий.

1.1.3. Играешь на равных – количество партий в матче не имеет значения, т.к. вероятность победить постоянна и равна 1/2.

1.2. Если не знаешь свои шансы – чем меньше партий, тем лучше. Оптимальный вариант – матч из одной партий.

Теперь оформим полученные результаты в виде таблицы:

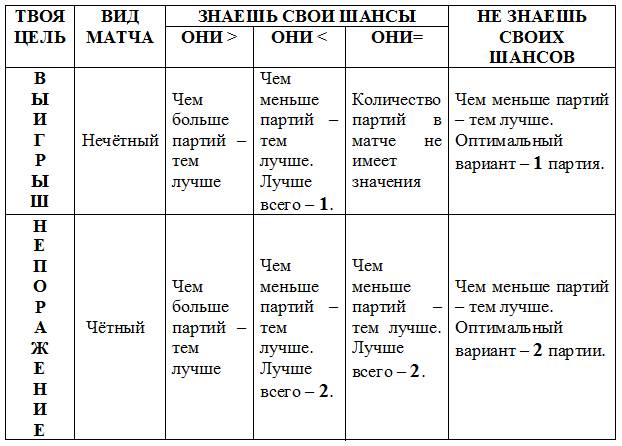
Следует сказать, что полученные результаты лишь идеальная математическая модель. Данная модель не учитывает того, что шансы игроков во время проведения матча могут меняться, например, в зависимости от их игровой выносливости, обучаемости. Но вообще – это хорошие «рабочие» правила.

К тому же (в первую очередь начинающим игрокам) я бы посоветовал просто играть в своё удовольствие, не задумываясь обо всех этих математических премудростях, с равными по силе игроками.

Глава 3 ТЕОРИЯ ФУТБОЛА НА БУМАГЕ

ТАКТИКА

Под тактикой в ФУТБОЛЕ НА БУМАГЕ подразумевается некий ход или последовательность ходов, совершаемых с целью достижения определённого результата. Как правило – с целью создать определённую конструкцию в поле, чтобы обеспечить себе выгодное положение или создать безвыходное положение для противника. То есть, тактика – это решение локальных задач, наиболее типичные приёмы, с помощью которых реализуется общий план.

1. Тактические приёмы игры – «маленькие футбольные хитрости».

К тактическим приёмам ФУТБОЛА НА БУМАГЕ относятся:

1.1. Перекрытие хода;

1.2. Чётный выход;

1.3. Создание безвыходного положения на стороне ворот противника – атака;

1.4. Создание безопасного положения на стороне своих ворот – защита.

1.1. Перекрытие хода.

Это самый распространённый приём, который используется чаще других. С его помощью можно:

1) создать безвыходное положение противнику (атака);

2) занять выгодное положение – построить «закрытую четверку»;

3) спастись от создания тебе безвыходного положения (защита).

1). Создание безвыходного положения противнику.

А) Самой простой моделью такого положения является – полное перекрытие прохода к твоим воротам. На рисунке 19 приведён пример такого перекрытия:

Из рисунка видно, что проход к Верхним воротам (В) полностью закрыт. Однако Верхнему игроку (В) не надо торопиться и сразу рваться к Нижним воротам (Н), т.к. противник может также перекрыть проход к своим воротам и тогда Верхний игрок (В) может проиграть. Всё, что требуется от Верхнего игрока (В) в данном положении – это методично заполнять пустые пересечения, «спускаясь» к воротам противника (это пересечения: c5; d5; b4; c4; d4; e4; f4), и только затем забить ему гол.