
Полная версия
Размышления о природе вещей и идей
2. Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.
3. Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота света ωmin (зависящая от химической природы вещества и состояния поверхности), ниже которой фотоэффект невозможен.
Эйнштейн выдвинул тезис, что не только излучение, но и распространение и поглощение света дискретны; позднее эти порции (кванты) получили название фотонов. Этот тезис позволил ему объяснить две загадки фотоэффекта: почему фототок возникал не при всякой частоте света, а только начиная с определённого порога, зависящего только от вида металла, а энергия и скорость вылетающих электронов зависели не от интенсивности света, а только от его частоты. Теория фотоэффекта Эйнштейна с высокой точностью соответствовала опытным данным, что позднее подтвердили эксперименты Милликена (1916).
Но главный триумф ожидал квантовую теорию, когда датский физик Нильс Бор дал объяснение структуры и свойств атомов, за что получил нобелевскую премию по физике в 1922 году. В предыдущем разделе мы упоминали, что планетарная модель атома, предложенная Эрнестом Резерфордом, неустойчива. Бор предложил принципиально новое объяснение устройства атомов. Три части революционной статьи «О строении атомов и молекул», опубликованные в журнале «Philosophical Magazine» в июле, октябре и декабре 1913 года, содержали квантовую теорию водородоподобного атома.
Для читателя особый интерес представляет ход мысли Бора, позволивший ему сформулировать положения новой физики, которые резко противоречили постулатам привычной физики Ньютона. Многие из нас застали то время, когда в домах присутствовало печное отопление. Такая печь имела чугунную плиту с конфорками. Растопив печь, в сумерках можно было наблюдать, как с повышением температуры плита светилась сначала тёмно-багровым цветом, затем цвет менялся на красный и позже на жёлтый. Известна фраза «довести до белого каления». Смысл её в том, что белый цвет плиты соответствует предельной температуре её нагрева. Сопоставив наблюдаемое с тезисом о том, что все вещества состоят из атомов, легко прийти к выводу, что именно атомы испускают свечение. Осталось выяснить механизм этого свечения.
Мы уже упоминали в первой части, что заряженная частица, движущаяся по криволинейной орбите, совершает работу, поэтому должна излучать. Такого рода излучение хорошо изучено для движения пучков или сгустков электронов в циклических ускорителях заряженный частиц. Оно называется синхротронным излучением, интенсивность такого излучения пропорциональня четвёртой степени частоты вращения электронов. Поскольку при этом частицы теряют кинетическую энергию, потери энергии нужно восполнять при прохождении частиц в зазорах резонаторов, иначе частицы упадут на стенки канала ускорителя. При потере энергии радиус траектории частицы плавно уменьшается, а частота обращения столь же плавно возрастает. При добавлении энергии непрерывно происходят обратные явления, поэтому спектр синхротронного излучения имеет диапазон, в котором представлены все частоты, непрерывно его заполняющие. Впервые непрерывный спектр излучения в видимой области наблюдал Исаак Ньютон в 1666 году, разложив белый свет с помощью треугольной призмы. То, что он увидел напоминало радугу на небе после дождя. В течение начала 1800-х Йозеф фон Фраунгофер сделал экспериментальные достижения с дисперсионными спектрометрами, которые позволили спектроскопии стать более точной и количественной научной техникой. С тех пор спектроскопия играла и продолжает играть значительную роль в химии, физике и астрономии. К началу ХХ века были накоплены огромные массивы экспериментальных данных о спектрах всех известных химических элементов и о многих молекулах наиболее часто встречающихся веществ. Оказалось, что все спектры имеют линейчатый характер, то есть состоят из конечного числа отдельных линий. При этом уникальность набора таких линий для каждого элемента такого же рода, как папиллярный узор на пальцах человека. Это позволяет идентифицировать химический состав любого вешества с помощью спектрометра, просто нагрев до высокой температуры микрограмм этого вешества.

Линейчатые спектры некоторых атомов
Специалисты проделали колоссальную работу, пытаясь классифицировать отдельные участки спектров, которые образуют серии линий. Так у атома водорода имеются серии Лаймана, Бальмера, Пашена, Брекета, Пфунда, Хэмпфри, Хансена-Стронга. Зная достаточно точно частоты излучения отдельных линий, экспериментаторы пытались подобрать простые эмпирические формулы, которые описывали бы целиком серию линий. Так Ридбергом была получена формула, описывающая спектральные серии
1/λ = R (1/n02 – 1/n2).
Здесь λ – длина волны линии излучения, R = 109677 см-1 – постоянная Ридберга для водорода, n0 – основной уровень серии. Так, для серии Бальмера n0 = 2, n = 2,3,…
Ещё немного подумав, можно догадаться, что, кроме равномерного и прямолинейного движения, в природе есть также резонансное циклическое движение, которое может совершаться без потерь энергии. Примером такого движения служит хорошо изученный математический маятник, отличающиймя от реального маятника отсутствием трения в точке подвески. В науке подобные объекты называются гармоническими осцилляторами. Их отличие от прочих объектов состоит в том, что маятник определённой длины L может колебаться не с любой частотой, а только с частотами, кратными основной резонансной частоте ω2 = g/L, где g – ускорение свободного падения.
Теперь остался один шаг, чтобы догадаться, что электрон на орбите – тот же гармонический осциллятор, L – радиус его орбиты, только константу g следует заменить, поскольку его колебания обеспечиваются не силой гравитации, а кулоновской силой притяжения к ядру. Именно поэтому осцилляторы-электроны в оболочках атома не могут находиться на орбитах с произвольным радиусом.
В теории Бора можно выделить два основных компонента: общие утверждения (постулаты) о поведении атомных систем, сохраняющие своё значение и всесторонне проверенные, и конкретная модель строения атома, представляющая в наши дни лишь исторический интерес. Постулаты Бора содержат предположения о существовании стационарных состояний и об излучательных переходах между ними в соответствии с представлениями Планка о квантовании энергии вещества. Модельная теория атома Бора исходит из предположения о возможности описания движения электронов в атоме, находящемся в стационарном состоянии, на основе классической физики, на которое накладываются дополнительные квантовые условия (например, квантование углового момента электрона). Теория Бора сразу же позволила обосновать испускание и поглощение излучения в сериях спектра атомов водорода. Теория излучения атомов основывается на трёх постулатах Бора:
Первый постулат носит название постулата стационарных состояний, гласит: каждому из стационарных (квантовых) состояний, в котором находится атом, соответствует определенный уровень энергии Е. Находясь в стационарном состоянии, атом не излучает.
Второй постулат носит название правила частот. Он гласит, что переход атома из одного квантового состояния, характеризующегося энергией En в новое квантовое состояние, которое характеризуется энергией Em, происходит излучение или поглощение кванта энергии. Энергия кванта при этом определяется как разность энергий двух квантовых состояний: hνnm=En—Em.
Третий постулат: Правило квантования. Он утверждает, что электрон, если атом находится в стационарном состоянии, движется по круговым орбитам, имеет дискретные квантовые значения момента импульса.
Набор числовых параметров, характеризующих состояние электрона в атоме называется квантовыми числами. К таковым относятся, например, радиус (или номер) орбиты электрона, ориентация спина, момент импульса. Нильс Бор впервые сформулировал, что переход электрона с одной стационарной орбиты на другую осуществляется спонтанно (случайным образом) и мгновенно, то есть у перехода нет истории. Помимо постулатов, Бор сформулировал ещё два принципа квантовой механики.
Принципом соответствия называется утверждение о том, что поведение квантовомеханической системы стремится к классической физике в пределе больших квантовых чисел. Этот принцип ввёл Нильс Бор в 1923 году.
Принцип дополнительности представляет собой один из важнейших эвристических и методологических принципов в квантовой механике. Сформулирован Н. Бором в 1927 г. Согласно такому принципу, при полном описании квантово-механических явлений требуется применение двух дополнительных (взаимоисключающих) наборов классических понятий, совокупность которых позволяет получить исчерпывающую информацию о таких явлениях, как о целостных. Дополнительными в квантовой механике считаются энергетически-импульсная и пространственно-временная картины.
В 1921 1923 годах в ряде работ Бору впервые удалось дать на основе своей модели атома, спектроскопических данных и общих соображений о свойствах элементов объяснение периодической системы Менделеева, представив схему заполнения электронных орбит (оболочек, согласно современной терминологии). Однако было очевидно, что теория Бора в своей основе содержала внутреннее противоречие, поскольку она механически объединяла классические понятия и законы с квантовыми условиями. Кроме того, она была неполной, недостаточно универсальной, так как не могла быть использована для количественного объяснения всего многообразия явлений атомного мира. Новой теорией стала квантовая механика, которая была создана в 1925 1927 годах в работах Вернера Гейзенберга, Эрвина Шрёдингера, Макса Борна, Поля Дирака.
Таким образом, во втором десятилетии ХХ века в Европе сложились два крупных центра научных исследований: в области экспериментальных исследований атома – Кавендишская лаборатория Эрнеста Резерфорда в Англии и Копенгагенский институт теоретической физики Нильса Бора в Дании. У Бора стажировались многие крупные физики, создавшие математический аппарат квантовой механики – Вернер Гейзенберг, Эрвин Шрёдингер, Макс Борн, Поль Дирак, Лев Ландау, Хендрик Крамерс, Оскар Клейн, Виктор Вайскопф, Леон Розенфельд, Джон Уилер, Феликс Блох, Оге Бор, Хендрик Казимир, Ёсио Нисина, Кристиан Меллер, Абрахам Пайс и другие.
В итоге плодотворной работы сложились две школы квантовой механики – Геттингенгская, возглавляемая Гейзенбергом и Копенгагенгская по руководством Бора. В основе геттингенгской школы лежит матричная механика Гейзенберга, основанная на понятии S-матрицы переходов квантовой системы из одного состояния в другое. Сам переход не имеет истории, то есть совершается мгновенно, а элементы матрицы описывают вероятность переходов. Математический аппарат геттингенгской (волновая механика) школы основывается на волновом уравнении Шрёдингера для комплексной ψ-функции, квадрат модуля которой представляет вероятность нахождения квантовой системы в заданном состоянии. Позднее Шрёдингер доказал эквивалентность обоих подходов в отношении экспериментально измеряемых величин.
Свойства квантовых объектов оказались весьма необычными. Например, определённые пары динамических переменных (например, координата-импульс, энергия-время) оказалось, в принципе, невозможно измерить одновременно с любой заданной точностью. Погрешность их измерения ограничивается соотношением неопределённости Гейзенберга Δx·Δp ≥ h/2, где h – постоянная Планка. Это свойство объясняется тем, что в микромире понятие измерения носит принципиально иной характер, чем в макромире, поскольку в процессе измерения участвуют объекты с разными свойствами: квантовый объект (частица или атом) и классический макрообъект (измерительный прибор). Пояснить это можно так. Когда мы наблюдаем (измеряем) параметры полёта камня или самолёта, в процессе измерения участвуют измеряемый макрообъект, световой луч (поток фотонов) и человеческий глаз, в который этот луч принёс информацию о маркообъекте. Поскольку кинетическая энергия светового луча на огромное число порядков меньше энергии объекта, воздействие луча на движение объекта пренебрежимо мало. Здесь световой луч является частью измерительного прибора. Именно это обстоятельство позволяет проводить измерения с любой, наперёд заданной, точностью. Если же таким образом измерять координаты микрочастицы, точность измерения нельзя сделать выше, чем длина волны фотона. Чем выше желаемая точность измерения, тем большей частоты следует брать фотоны. Это значит, тем большей энергией они должны обладать. Поскольку кинетические энергии фотона и частицы одного порядка, это означает, что фотон с большей энергией так «ударит» по частице, что после измерения её координаты энергия и импульс частицы изменятся радикальным образом. Кроме того, Луи де Бройль показал, что любой частице с импульсом р можно сопоставить длину волны λ = h/p. Это означает, что координаты этой частицы-волны невозможно измерить с точностью, меньшей длины её волны. Такие свойства квантовых объектов получили название корпускулярно-волнового дуализма. Мгновенность переходов из одного квантового состояние в другое, вообще не позволяет делать какие-то предположения о скорости микрообъектов при таких переходах. Это означает, что в микромасштабах постулаты специальной теории относительности неприменимы.
Итак, мы показали, что существуют пределы делимости не только для вещества, но и для энергии. Последним бастионом при переходе от непрерывного мира к дискретному оказались такие категории, как пространство и время.
Эволюция представлений о пространстве и времени
За последние пять тысячелетий человеческой цивилизации представления о времени и пространстве претерпели неоднократные, порой радикальные изменения. В своём кратком очерке я не ставлю своей целью осветить всю историю этих изменений. Ограничусь лишь теми из них, которые можно считать «верстовыми столбами» этой истории. С начала цивилизации и практически до эпохи классической физики, которую принято называть ньютоновской, было принято считать, что пространство – это вместилище тел, не имеющее материальных атрибутов (абсолютное пространтво). Оно имеет как бы невидимые «полочки», на которых эти тела располагаются. Время – это темп развития Вселенной. Он задан богами, космическим разумом или Природой, поэтому на него никак нельзя воздействовать, его нельзя изменить (абсолютное время). Движение представляет собой плавное «перекатывание» тел с одной полочки на другую с разным темпом, называемым скоростью. В природе нет естественных шкал для измерения расстояний в пространстве и интервалов времени, поэтому такие шкалы являются предметом договорённостей между людьми. Одни измеряют расстояния в милях и дюймах, другие в вёрстах, саженях и аршинах, третьи в километрах, метрах и миллиметрах. Одна из таких шкал хранится в парижской палате мер и весов в виде платиново-иридиевого стержня («католический метр»), длина которого составляет одну сорокамиллионную часть парижского меридиана (1791 г.) или расстояние, проходимое светом за 1/299 792 458 секунды (1963 г.). Для введения шкалы времени использовались природные циклические процессы – время обращения Земли вокруг своей оси (сутки), время смены фаз Луны (лунный месяц), время обращения Земли вокруг Солнца (год). В Вавилонии после 300 года до н. э. день делился шестидесятирично, то есть на 60, полученный отрезок – ещё на 60, потом – ещё раз на 60. Жители древнего Египта делили дневную и ночную половины суток каждую на 12 часов уже, по крайней мере, с 2000 года до н. э. В силу разных длительностей ночного и дневного периодов в разное время года продолжительность египетского часа была величиной переменной. Греческие астрономы периода Гиппарх и Птолемей делили день на основе шестидесятиричной системы счисления и также использовали усреднённый час (1⁄24 суток).
На Рисунке 1 представлены физические теории, отражавшие представления человечества о природе материального мира. Показанные здесь оси представляют малые параметры: G – гравитационная постоянная, введённая в законе всемирного тяготения Исааком Ньютоном; 1/c – обратная величина скорости света; h – постоянная Планка. История представлений физических моделей мира начинается с начала координат, которое соответствует отсутствию гравитации в моделях движения со скоростями, пренебрежимо малыми по сравнению со скоростью света. При этом представление об атомах, предсказанных Левкиппом и Демокритом, не входили в картину мира. Такую модель мы называем кинематикой Галилея. В своём принципе относительности Галилей выделяет равномерное прямолинейное движение, которое не требует вмешательства внешних объектов, служащих причинами движения. О причинах других движениях на этом этапе не говорится ничего определённого. Их можно считать мистическими. Свойства простанства, где происходят движения, описываются геометрией Евклида.
Аристотель считал, что движение от покоя отличается наличием скорости. Для начала движения к телу необходимо приложить силу, поэтому скорость пропорциональна приложенной силе. Такая модель способна объяснить движение телеги, которую катит лощадь по дороге, но неспособна объяснить, почему телега катится с горки, не понуждаемая лошадью. Впервые уравнения динамики движения сформулировал Ньютон в своём втором законе динамики. В его модели ускорение, приобретаемое телом пропорционально приложенной к телу силе и обратно пропорционально массе тела. Чтобы получать решения уравнения динамики, Ньютону пришлось разработать новую математику – исчисление флюксий. Дальнейшее развитие этого раздела математики было названо дифференциальным исчислением. Одной из главных заслуг Ньютона было открытие закона всемирного тяготения, в котором впервые было описано фундаментальное взаимодействие всех объектов природы, названное гравитацией. Значение этого закона трудно переоценить, потому что он позволил объяснить причины и траектории движения всех планет солнечной системы и вычислять их параметры с поразительной точностью. У Птолемея, например, планеты на небесных сферах двигали ангелы, поочерёдно сменявшие друг друга. Геометрические свойства движений в ньютоновской физике описываются дифференциальными формами Картана. Физика Ньютона получила своё блестящее завершение созданием аппарата аналитической механики трудами Даламбера, Моперюи, Лагранжа, Эйлера, Гамильтона и других.
Революционным шагом в развитии представлений о пространстве и времени было опубликование Альбертом Эйнштейном в 1905 году в «Анналах физики» статьи «К электродинамике движущихся тел», которая описывает основные положения специальной теории относительности. Фундаментом этой теории являются два постулата:
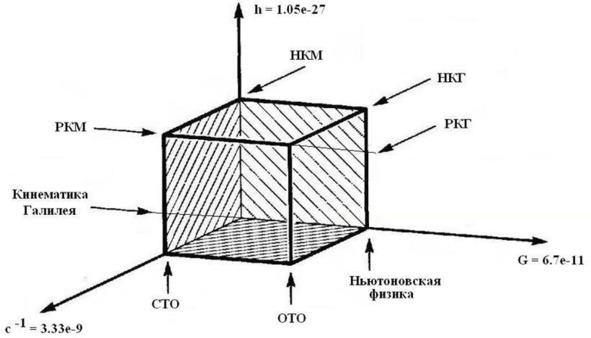
Модели физической реальности
1) постулат относительности: законы физики инвариантны в любых интерциальных системах;
2) скорость света постоянна и одинакова во всех интерциальных системах.
Следует сказать, что в этой области у Эйнштейна были предшественники. Анри Пуанкаре опубликовал представления о четырёхмерном пространстве-времени в 1900,1903 гг., Хендрик Лоренц опубликовал свои преобразования в 1892, 1895 гг., но именно Эйнштейн собрал воедино эти представления, сформулировав их в виде законченной физической теории, позволившей объяснить единым образом результаты экспериментов Альберта Майкельсона по измерению скорости света, сокращения расстояния и роста массы при ускорении заряженных частиц. Математический аппарат СТО базируется на четырёхмерной псевдоевклидовой геометрии Минковского.
Дальнейшим развитием СТО стала общая теория относительности Эйнштейна, математический аппарат которой разработан математиком Грассманом и основывается на тензорном анализе в обобщённых криволинейных геометриях Римана. ОТО дала дальнейшее развитие закона всемирного тяготения Ньютона и позволила объяснить законы эволюции Вселенной, построить теорию «чёрных дыр». В рамках этой теории гравитационное поле локально эквивалентно ускорению, источники поля не являются первичными объектами, их локализация определяется коэффициентами кривизны физического пространства. Знаменитый эксперимент с падающими лифтами демонстрирует, что в системе свободно падающего лифта гравитация исчезает, но она не исчезает во всём пространстве сразу. Далее мы приводим сравнительные характеристики пространства, времени и движения в классической физике Ньютона и новой физике ХХ века.
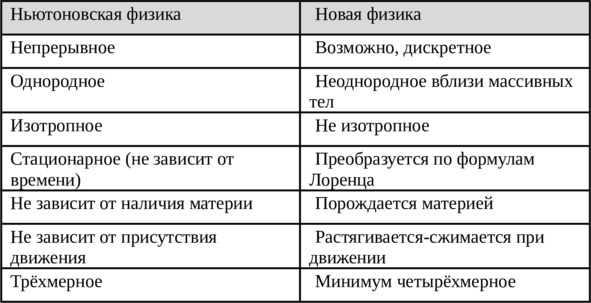
Эволюция представлений о пространстве
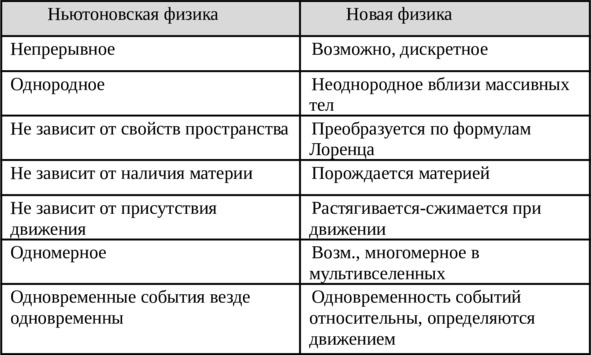
Эволюция представлений о времени
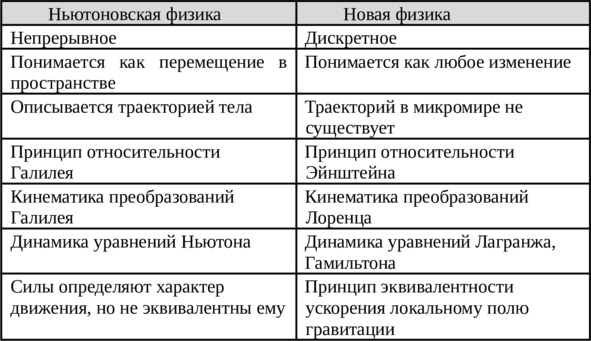
Эволюция представлений о движении
Мы описали развитие человеческих представлений о материальном мире от кинематики Галилея в направлениях учёта эффектов гравитации и скоростей, сравнимых со скоростью света. Примечательно, что во всех физических теориях используется математический аппарат непрерывных функций, представляющих свойства геометрии пространства-времени. Нет ничего удивительного в том, что сходный аппарат непрерывных функций, несколько расширенный в область комплексных функций и операторов, стал использоваться, когда физики стали развивать новые модели квантовой механики микромира. Типичным примером является волновое уравнение Шрёдингера для комплексной пси-функции
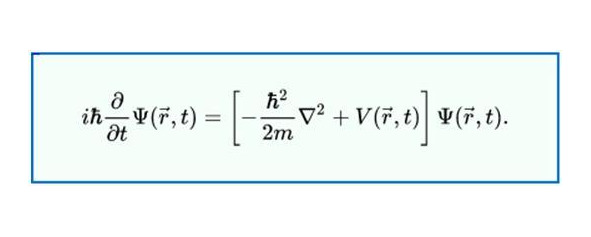
Волновое уравнение Шредингера
То же самое в уравнении Гейзенберга для комплексной матрицы перехода А
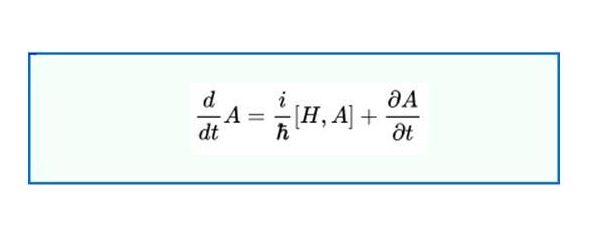
Матричное уравнение Гейзенберга
В обоих случаях используются операции дифференциования по времени и пространственным координатам. Иными словами, в новых теориях использовалась геометрия непрерывных комплексных четырёхмерных пространств. В релятивистском обобщении уравнение Шрёдингера заменяется на уравнение Дирака для той же пси-функции над пространством биспиноров.
Электрические и магнитные явления были объединены в единую электромагнитную силу в уравнениях Джеймса Клерка Максвелла в 1861 году. Электромагнитные и слабые взаимодействия получили объединение в теории электрослабых взаимодействий С. Вайнсберга, Ш. Глэшоу и А. Салама в конце 60-х годов ХХ века. Добавление к ним сильных взаимодействий завершилось созданием стандартной модели элементтарных частиц примерно к тому же времени. Эта модель была слегка дополнена открытием в 2012 году бозона Хиггса. Ожидаемые следующие шаги – включение в расширение стандартной модели тёмной материи и гравитационных сил. Попытки объединения гравитационного и электромагнитного поля в рамках 4-мерных геометрий были предприняты Г. Вейлем и А. Эддингтоном. Более плодотворной оказалась попытка Теодора Калуцы с введением в геометрию пространства-времени пятой координаты (1921 год). Обобщения теории Калуцы были сделаны О. Клейном и В.А.Фоком в 1927 году. Затем последовали публикации А. Эйнштейна и Луи де Бройля с обобщениями ОТО и электродинамики в 5-мерной геометрии с развитием идей Калуцы (1927 год). Ненаблюдаемость пятой координаты, оказалось, связана с тем, что мир замкнут по этой координате, её период составляет десять в минус 33-й степени метра, и он определяет элементарный заряд (электрона). Так физики впервые столкнулись с проблемой свёрнутых измерений геометрии пространства-времени. Это обстоятельство породило гипотезу, что вначале Вселенная была свёрнута по всем измерениям, но на каком-то этапе её эволюции произошло размыкание по четырём измерениям – трём пространственным и времени. Ю. Б. Румер в начале 50-х годов в своей книге «Исследования по 5-оптике» вводит пятую координату для геометризации квантовой механики. Здесь пятая координата имеет физический смысл действия, а её период равен постоянной Планка. Ю. С. Владимиров в своей книге «Пространство-время» пишет: «Главная причина неудач с теориях Румера и Калуцы-Клейна состоит в том, что с помощью одного дополнительного измерения пытались решить две совершенно различные задачи: описание электромагнетизма и введение в теорию масс покоя частиц. С позиций сегодняшнего дня представляется, что каждая из названных задач должнв решаться с помощью отдельной размерности, т.е. теория, нацеленная на совместное решение обеих этих задач, должна строиться в рамках 6-мерного пространственно-временного многообразия». Причины, по которым теории квантовой гравитации НКГ и РКГ не были завершены, обсуждаются ниже.






