Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей

– Я могу убедить математика, живущего на плоскости, что если бы он смог прибегнуть к помощи трехмерного пространства, то без труда заменил бы левую стельку правой и наоборот. А для нас, трёхмерных существ, так можно было бы поступить с ботинками, а именной взять левый ботинок перевернуть его в четырёхмерном пространстве и получить правый и опять же наоборот из правого -левый!

– Я об этом где-то читал в детстве, – задумчиво заметил Борщов.

– Но ведь пространство больше трёх, ну может быть ещё четырехмерное с добавлением оси времени, – задумчиво сказал вслух Татьяна, – словом такие фигуры существуют лишь в нашем воображении, они выдуманные, а не реальные

– А реальны ли отрицательные числа? А комплексные числа? – вдруг спросил Борщов. Матвей приготовился ответить, но Борщов кивком головы дал ему понять: позвольте мне, коллеги, это быстро объяснить простыми словами. – Отрицательные числа используется в финансах и бухгалтерии, без них невозможна работа рыночной экономики, то есть мы сопоставляем отрицательным числам реальные объекты: банковский кредит, налоги и так далее. Что касается комплексных чисел, то они упрощают работу с радиоволнами, оптикой. У каждого из Вас мобильник – это реальность? Безусловно. Что касается физических формул, то в них используются пятые, шестые и более высокие степени, аналогичная ситуация в социологии, маркетинге – другими словами, гиперкубы моделируют материальные объекты. Продолжайте, пожалуйста, Матвей.

И Матвей продолжал:

– Гиперкуб обладает свойством симметрии. Если расположить начало координат в центре гиперкуба, то каждая его вершина будет находится на расстоянии половина ребра a умножить на квадратный корень √n, что легко вычисляется по теореме Пифагора. Перпендикуляр, опущенный из центра гиперкуба на любую его грань, проходит через её центр и длина образуемого отрезка (высоты любой из совершенно одинаковых из 2n гиперпирамид, на которые рассекается гиперкуб составляет половину ребра гиперкуба ½а). Легко убедиться, что грань гиперкуба – это гиперкуб размерности на единицу меньше…

– А я видел фильм про гиперкуб! – вдруг перебил его Артур. -Там он как- то странно крутился на шарнирах…

– Да, это тессеракт, – подтвердил Матвей или четырехмерный гиперкуб, но его показывают с эффектом параллакса или о степенях выше трёх мы ещё поговорим, а пока достаточно сравнить двухмерный, он показал на шахматную доску и трёхмерный случаи, и он коснулся фигуры из деревянных кубиков.

Давайте рассечем нашу фигуру из трёх вложенных друг в друга гиперкубов на равные гиперпирамиды, конкретно квадраты мы рассечем прямыми линиями на четыре треугольника, а кубы – на шесть совершенно одинаковых пирамид, как раз по числу граней.

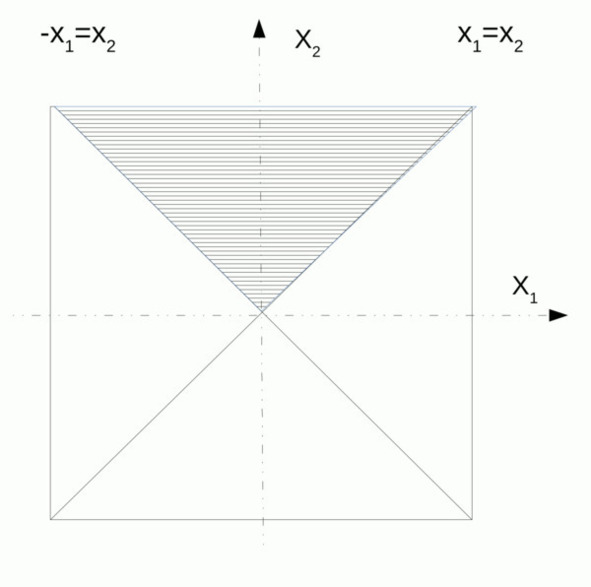
Рис. 2.4. Рассечение гиперкуба. Случай двумерного пространства. Обратите внимание на уравнения x2 = x1 или привычнее y = x – это линяя под углом 45 градусов или биссектриса угла. Подумайте, как будут расположены точки на прямой, описываемой уравнением x2 =-x1

– А почему они будут одинаковы? – задумчиво спросил Борщов.

– Потому что каждая пирамида имеет одинаковую высоту, равную как раз половине ребра гиперперкуба и основания каждой пирамиды одновременно являются гранями гиперкуба, а в силу симметрии грани между собой конгруэнтны, проще говоря равны. Более того эти пирамиды правильные, их грани равны и боковые ребра равны, поскольку являются полудиагоналями гиперкуба, что составляет a * √n /2.

– Ага, вижу ….

Рис. 2.5. Рассечение гиперкуба. Случай трёхмерного пространства.

– Матвей, ты хочешь сказать, что эти пирамиды также вписаны друг в друга: большая, малая и средняя? – спросила его Татьяна.

– Да, они также вписаны как и гиперкубы, но я их не стал изображать, чтобы не затруднить восприятие.

– Я кажется догадалась, ты сейчас расскажешь нам о симметрии! – предвосхитила с улыбкой Татьяна.

– Совершенно точно! – ответил Матвей. Все, что касается соотношения объёмов гиперкубов повторяется и для этих пирамид, но в силу симметрии мы можем сфокусироваться лишь на одной пирамиде, если хотите, называйте гиперпирамиде, но первое проще…

– Матвей, вдруг заговорил после небольшой паузы Борщов, – если Вы всё-таки склоняется нас в пользу геометрической наглядности, то не могли бы Вы сформулировать и саму Великую теорему в геометрической форме?

– С радостью! – ответил Матвей. Он перелистнул пару листов и наконец с расстановкой зачитал:

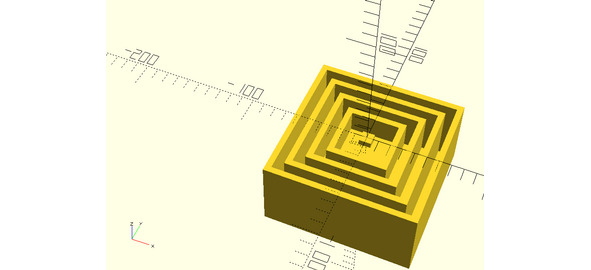
Формулировка теоремы Ферма в геометрической форме

+++++++++++++++++++++++++++++++++++++++++++++++++++++++

В n-мерном пространстве объем a-Малого гиперкуба (объединение 1n и последовательное наращивание k слоёв) прибавить объем b-Среднего гиперкуба (наращивание ещё l слоёв) образует объем c-Большого гиперкуба (ещё m слоёв). Ребра гиперкубов – целые числа. Все слои следуют последовательно и непрерывно, пронумерованы натуральными числами. Чтобы правая и левая часть уравнения Ферма были равны, необходимо соблюдение ряда условий:

с одной стороны:

центральная симметричность фигуры в виде трёх вложенных гиперкубов, непрерывность следования слоёв, их полное заполнение гиперкубиками

с другой стороны:

объём a-Малого гиперкуба равен объему множества точек между с-Большим и b-Средним гиперкубами.

При n> 2 эти условия являются взаимоисключающими и невыполнимы.

+++++++++++++++++++++++++++++++++++++++++++++++++++++++

Легко убедиться на примере любой (обозначается как ∀) Пифагоровой тройки, что последнее условие, в случае такой тройки, выполняется в двумерном пространстве, т.е. для вписанных друг в друга квадратов. Формула теоремы Ферма – это аналог теоремы Пифагора, но в n-мерном пространстве. Если хотя бы Пифагорова тройка в n-мерном пространстве найдется, то Теорема Ферма и его уравнение будут опровергнуты.

– Пока все понятно, кроме слоя, что это такое? – спросил Борщов.

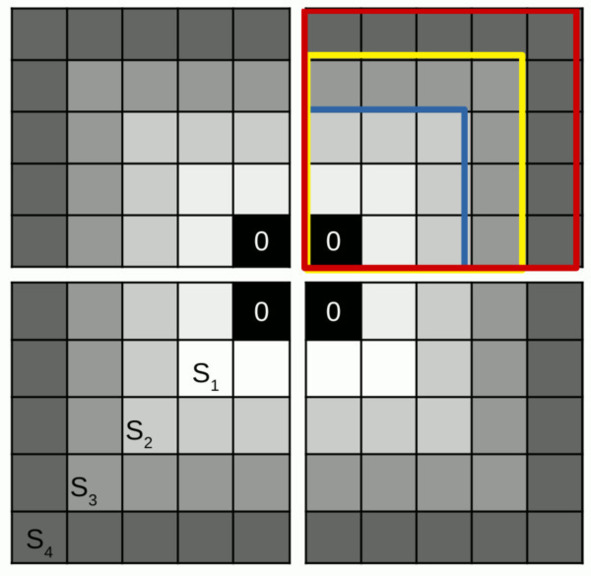
– Строго математически мы вводим определение слоя S как множества точек в n – мерном пространств, полученное в результате разности множеств точек вписанных друг в друга гиперкубов, с общей вершиной, рёбра которых отличаются на единицу, как на экзамене ответил Матвей (см. Рис 2.2.).

– А если не вершины, а центры гиперкубов общие, – указав на шахматную доску, сказала Татьяна, – то рёбра гиперкубов, ограничивающие слой будут отличаться на двойку?

– Абсолютно точно! – кивнул Матвей. – Но мы будем выбирать то или иное множество фигур.

1) множество фигур «начало координат в вершинах» вписанными друг в друга гиперкубов, совмещенных по произвольной вершине

или

2) в «начало координат в центре всех трёх гиперкубов an, bn, cn».

Обе геометрических фигуры соответствующих каждому из только то заданных множеств точек пространства, преобразуются друг в друга за счет отражений от гиперплоскостей, перпендикулярных каждой из n осей координат либо рассечения фигуры на «гиперквадранты» и масштабирования. Вспомните наши эксперименты с салфеткой! – Матвей схватил со стола сложенную дважды пополам салфетку и продемонстрировал ее всей компании.

– Под термином гиперквадрант понимается, например, подпространство только неотрицательных значений … – Матвей приготовился выдать строгое определение но его перебили.

– Проще говоря это салфетка сложенная на четыре части, а точнее её малый квадратик? – задала наводящий вопрос Татьяна.

– Да

– Ну так и скажи, мы же не на экзамене – назидательно сказала Татьяна.

– Итак, коллеги, для начала неплохо, очень даже неплохо, начала подытоживать встречу Борщов. – давайте опишем какое примерно это должно быть это направление, вернее, где может скрываться доказательство? И Борщов, пригласил широким жестом высказаться каждого.

Оно должно быть очевидным, и на первый взгляд, совершенно невероятным

– задумчиво произнесла Татьяна.

Его можно понять с минимальным количеством формул или совсем без формул

– добавил Матвей.

Все посмотрели на одиннадцатилетнего Артура – собравшись духом, он каким-то официальным тоном сказал:

Такое доказательство должен понимать любой потребитель, категории двенадцать плюс!

– Вот как глубоко в нашу жизнь проник маркетинг! – назидательно шутя заметила Татьяна. А в целом, – продолжала Татьяна: хорошо бы провести опрос среди знакомых и знакомых их знакомых (вот здесь как раз и могут пригодиться социальные сети!), кто сможет пересказать по памяти доказательство Великой теоремы Ферма? За исключением от силы сотни математиков – Гуру в теории чисел и лиц с фотографической памятью, способных точно запомнить полторы сотни страниц текста, этого не сможет сделать никто!

– Именно поэтому поиск Истины и наглядных доказательств нельзя остановить с присуждением Абелевской премии, заметил Борщов.

Итак группа выработала основные правила

встречаться каждую в неделю;

терпеливо перебирать разные варианты, даже немного крейзи, тщательно прорабатывать детали;

«не залезать в дебри»;

искать простое наглядное доказательство, понятное школьнику средних классов школы;

и не посещать Всемирную паутину, соцсети без самой крайней необходимости.

Последнее условие выдвинул Борщов, объясняя это тем, что Всемирная паутина и антисоциальные, как он любил их называть, сети, особенно те, которые выполаскивают мозги, наполняя их приколами и всяким мусором, сильно ограничивают наше творческое воображение. Во-первых, это отрицательный опыт других «лузеров» (Борщов при этом выразительно посмотрел на Артура), которые искомого доказательства не нашли, и наводят на искателей излишние комплексы во-вторых, это постоянные манипуляции сознания и сбивание с толку. Какие-то всезнайки постоянно кричат: это невозможно, это делается лишь так-то и так-то, только у нас о ты, ничтожнейший, получишь шанс со скидкой и так далее… Не даром старина Манфред Шпитцер написал свою скандальную книгу: «Цифровая деменция или антимозг»

[Шпитцер Манфред Антимозг: цифровые технологии и мозг/ Манфред Шnитцер; пер. с немецкого А. Г. Гришина – Москва: АСТ, 2014. – 288 с. ISBN 978-5-17-079721-9].

Ребята приводили аргументы против цифрового «аскетизма», восхваляя работу в группах в коллаборации, плюсы Всемирной паутины, но затем согласились, что не будут читать, смотреть ничего кроме недостающей литературы и переводов на английский язык специальных терминов, на месяц или даже больше заблокируют свои аккаунты в сетях для того, чтобы мобилизоваться к достижению общей цели. Матвей не смог сдержать улыбки вспоминая кличку Борщова – Борщ или профессор кислых щей: когда надо профессор мог быть удивительно занудным и упрямым.

Александр Николаевич молча положил кнопочный мобильник на стол и кивнул на него: дескать, обычной звонилки достаточно, в крайнем случае SMS.

– Словом, звучит все это грандиозно! – прихлопнул в ладоши профессор, и ребята знали: это означает конец диалога и одновременно то, что он доволен встречей.

И тут раздался сигнал бип-бип на часах у Матвея, который вскочил словно ошпаренный кипятком: Ой, у нас начинается День физики в нашей школе, а наш класс отвечает за расстановку приборов для демонстрации экспериментов, у меня осталось уже меньше часа, так что я лечу!

И Матвей оставил дружную компанию единомышленников на самом интересном моменте.

– Ну, уважаемые коллеги, какие ещё у нас остались вопросы? – обращаясь к Татьяне и Артуру подытожил Борщов.

– А почему Вы называете это место Собачьи бутерброды? – совершенно серьёзно спросил Артур.

Татьяна широко улыбнулась.

– Так называется эту пищу на её родине, – пояснил профессор. – Есть такая старая добрая американская комедия Выйти замуж за миллионера, вырастешь – посмотришь :-)

Первые эксперименты

Артур взял пачку стандартный офисной бумаги формата А4, 500 листов я аккуратно распаковал с малой стороны, затем с помощью Татьяны вынул бумагу из пачки чтобы на столе получилось стопка бумаги, уложенная аккуратно в параллелепипед.

– Давай наклоном слегка эту стопку бумаги в бок, сказала Татьяна, чуть влево или вправо. Артур взял цифровой фотоаппарат и отснял полученную фигуру с разных сторон, как принято на уроках черчения: вид сбоку, вид спереди. Скоро фотографии были выведены на большом экране отцовского компьютера.

– Я думаю, ты стреляешь из пушки по воробьям, – заметила Татьяна, – тебе достаточно было обычной металлической линейки, вот эта с миллиметровой шкалой подходящая.

– Но так я смогу провести настоящий эксперимент! – горячо возразил Артур, – и останутся фото результатов, как учил нас Александр Николаевич.

Повторите и найдите ответы

Попробуйте рассчитать толщину листа, исходя из толщины пачки бумаги и количества листов. Затем рассчитайте площадь двумерной фигуры параллелепипеда и его половины – треугольника.

Можно ли утверждать, что площадь двумерной фигуры, которую видит наблюдатель, остаётся постоянной при смещении стопки листов аккуратно в бок, или нельзя?

Что произойдет с итоговой площадью фигуры, если бумага станет толще?

Напомним, что стандартная офисная бумага весит 80 грамм в расчёте на один квадратный метр, есть и более тонкие и соответственно, толстые листы: 180 грамм/ м2, 360 г/ м2.

Представьте себе катушечный (кассетный) магнитофон. Верно ли утверждение, что сумма квадратов радиусов на бобинах кассет остаётся постоянной?

Рис. 2.6. Сумма квадратов радиусов бобин магнитофонной плёнки остается приблизительно постоянной. Почему?

Аналогичный вопрос для клубков шерсти, перематываемых бабушкой при вязании: верно ли утверждение, что сумма кубов радиусов обоих клубков остаётся примерно постоянной? Для простоты можно условно считать, что шерстяная нить несжимаема.

Спичка длиной в один метр

Вечером Артур с отцом поехали закупать бруски и рейки для строительства навеса от дождя над крыльцом дачи. Отец ходил по рядам вертикально расположенных брусков и реек, внимательно рассматривая пиломатериалы разных сечений и качества обработки.

– Вот и решай, Артур, где выгоднее купить: здесь или на базе? – задумчиво поговаривал отец, – у нас есть карточка на пятипроцентную скидку, но там цена определяется кубометрами заказа, за каждый кубометр древесины просят 8000 руб, а здесь…. а здесь счет идет поштучно за трёхметровые и четырехметровые рейки. Шестиметровые бруски, как на базе, лежат вон там в штабелях, – отец показал рукой.

Артур начал прикидывать в уме: погонажный пиломатериал на базе реализуется стандартными брусками и рейками по шесть метров длины, стоимость за один кубометр составляет 8000 руб. Попробуем посчитать все в кубических дециметрах или привычнее в литрах (ведь бывают жидкие гвозди! Наверное есть и жидкая древесина), допустим вот этот брус десять на десять сантиметров – это шестьдесят литров, а каждый литр древесины – это 8 руб., итого 480 руб. стоил бы этот шестиметровый брус на базе или 80 руб. за один погонный метр, что значит 320 руб. за четыре метра, а здесь 620 руб. за те же четыре метра.

– Папа, это грабёж! – радостно воскликнул Артур, наценка сто процентов от цены на базе!

Отец удивленно посмотрел на сына.

Вместе они легко рассчитали стоимость бруса сечением один квадратный сантиметр длиной шесть метров и даже один квадратный миллиметр – вот такая шестиметровая спичка по цене 5 коп. за штуку со скидкой 4%. В результате можно легко производить в уме расчет объёмов любых погонажных изделий: в одних случаях в сантиметрах, в других – в миллиметрах.

В итоге Артур с отцом купили в магазине только материалы тонкой обработки тонкие строганные рейки 10 х 20 мм, наличники для окон 10 х 70 мм в магазине, а остальное -на базе.

Практическое правило:

Для того чтобы быстро и удачно вести переговоры о цене, где требуется сопоставлять трудно сопоставимые объёмы, величины и быстро производить в уме расчёты, рекомендуется выбрать и рассчитать стоимостные и др. характеристики стандартных образцов (шаблонов), на основании которых можно легко производить несложные вычисления. Этот приём универсален, он используется в технике, военном деле, социологических исследованиях, и мы будем обращаться к нему неоднократно.

Смена масштаба не меняет сути явления, но помогает в расчётах.

Глава 3. Подготовка к восхождению

Основы комбинаторики. Треугольник Паскаля

Выходные родители Татьяны и Артура старались посвятить спорту. Погода была самая что ни на есть лыжная: солнце, мягкий лёгкий снег и полное безветрие. И семья из четырех человек решила поехать на базу Локомотив. С разрешения родителей Татьяна пригласила профессора Борщова и Матвея – благо в большом автомобиле семьи было ровно шесть мест. Между Артуром и Татьяной возник спор: кто где будет садиться в авто? Конечно место водителя – не в счёт, остаётся пять свободных мест. Для простоты можно условно считать, что в кресле первого ряда может сидеть как взрослый, так ребёнок. Сколько различных комбинаций возможно?

Перестановки, формулы комбинаторики

Допустим, что все пять пассажиров рассчитались по номерам: 1, 2, 3, 4, 5. Первый пассажир может выбрать любое из пяти мест, второй – любое из оставшихся свободных четырёх, третий – любое из свободных трёх и т. д. В результате имеем:

5 * 4 * 3 * 2 * 1 = 5!

Обобщение. Будем переставлять их всеми возможными способами n объектов, при этом их общее количество остается неизменными, меняется только их порядок. Получившиеся комбинации называются перестановками, а их число равно:

Pn =n! =1⋅2⋅3⋅…⋅ (n—1) ⋅n

Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n. По определению, считают, что 0!=1 и 1!=1.

Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов.

Число сочетаний

Теперь рассчитаем число сочетаний книг из библиотеки, буккроссинга. На первом этаже подъезда дома Татьяны и Артура инициативная группа создала полку для обмена книгами буккроссинг. Сегодня на полке осталось 7 книг, Все книги были интересными, но Артур решился позволить себе прочитать лишь три книги из-за высокой учебной нагрузки. Каково число вариантов выбора трёх книг из семи?

Чтобы найти ответ надо просто разделить все имеющиеся 7 книг на три подгруппы А, Б, В и мысленно осуществлять перестановки в каждой, их число будет

А) Всего в библиотеке 7 книг или 7! перестановок

Б) Дома у Артура 3 книги или 3! перестановок

В) Осталось в библиотеке 4 книги или 4! перестановок.

при этом не различимы варианты, когда книги остаются в пределах любой из подгрупп: не важно в каком порядке они следуют на полке дома у Артура или остаются стоять в библиотеке. Поэтому имеем:

Число сочетаний для случая буккросинга на полке дома Артура

а общая формула для расчёта числа сочетаний:

Биноминальный коэффициент или число сочетаний рассчитывается по это формуле

Смысл формулы заключается в том, что из возможных перестановок книг, перестановки на самой полке библиотеки буккросинга и личной полке читателя не имеют значения: такие перестановки рассматриваются как равнозначные сочетания. Следовательно общее число перестановок необходимо разделить на число перестановок на библиотечной полке и разделить также на число перестановок на читательской полке.

Число сочетаний это также биноминальный коэффициент. Происходит это наименование из Бинома Ньютона. Несложно раскрыть следующее выражения (a + b) n для случая n = 2, n = 3, n = 4 – легко убедиться, что образуется ряд в виде суммы произведений вида:

Бином Ньютона. С помощью этой формулы можно разложить выражение (a + b) n

здесь знак суммирования обозначается греческой буквой ∑, читается как сигма,

где целое m – это счетчик, пробегающий значения от 0 до n.

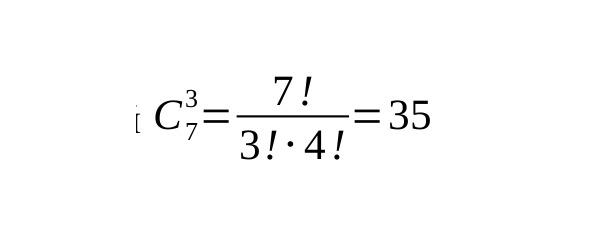
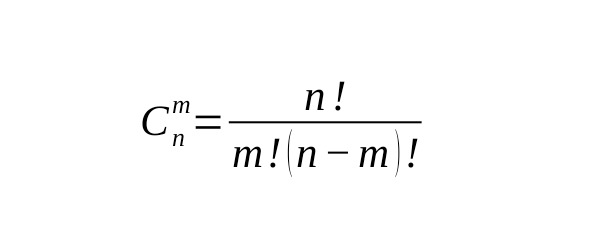
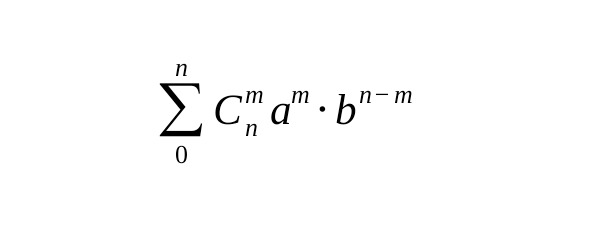
Треугольник Паскаля

Треугольником Паскаля называется треугольная таблица, в которой на вершине и по боковым сторонам расположены единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в строке выше (мысленно следует записать ещё по единице слева и справа самой верхней единицы):

1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

Как легко убедиться в каждом ряду стоит число сочетаний Cnm или биноминальный коэффициент.

Любопытно разложение: (1+1) n = ∑ Cnm

означающая, что сумма любого ряда всех биноминальных коэффициентов равна 2n например 1 +2 +1 = 22 – проверьте для более высоких степеней!

=========================

Родители и Артур взяли на прокат коньки и пошли на ледовый каток. Играла музыка, из-подо льда мигала светодиодная подсветка причудливыми узорами, играла приятная мелодия. Татьяна, Матвей и Борщов предпочли конькам лыжи. Они выбрали трассу Пятёрка – пять километров в хвойном лесу, где были такие причудливые холмы с неожиданными спусками и подъёмами.

Борщов шёл коньковым ходом впереди, плавно, легко, широкими шагами, вслед за ним плавно как на коньках следовала Татьяна, замыкал этот командный забег Матвей, часто семенящий на лыжах.

Борщов сделал небольшой круг, разворот и снова оказался позади Матвея.

– Дружище, надо бы толкаться плавнее, чтобы работали руки и пресс, – показал он Матвею. – Палочка ставится плавно чуть вперёд в сторону движения, корпус догоняет её и работает рука. Плавно налегаем. Ноги пружинят. В результате работа от приложения мускульных усилий преобразуется в кинетическую энергию. Все фазы движения должны быть согласованы.

– Я за этим не успеваю следить! – ответил Матвей.

– А следить и не надо – надо чтобы красота движения была отработана до автоматизма. Красота – это значит эффективное движение, это принцип наименьшего действия, есть такой в физике… И главное, ощущение хорошей внутренней игры, как говаривал старина Тимоти Голви!

На двадцать шестой минуте группа подошла к финишу.

– Неплохо, отметила Татьяна, – а давайте сдадим лыжи в прокат и посидим в кафе на лыжной базе, пока наши фигуристы катаются на коньках.

Всё пропало, все пропало!

Вся дружная компания прошла в кафе «Локомотив». Заказали чай и пирог с яблоками.

– Ну как продвигается дела с Великой Теоремой? – спросил профессор Борщов.

– Честно говоря, я даже не хотел идти на лыжах – ответил Матвей. – Все мои идеи оказались провальными. Я перепробовал пирамиды, квадратичную и другие системы координат, гиперцилиндры, гиперконусы и гиперкруги, но это заводило меня в такие дебри ….

Борщов понимающе кивал: дескать, ничего страшного, так оно и бывает. И рассказал анекдот Юрия Никулина о том, как в самолёте первым классом летела команда моряков. Все во главе с капитаном дружно уснули. И только бодрствовал попугай, который, сидя на спинке кресла капитана, снова и снова повторял: пр-р-ропали мы, пр-р-ропали! Скорчив гримасу Борщов рассказал этот анекдот, что называется «в лицах». Все дружно рассмеялись и напряжение исчезло. Еще продолжая смеяться, Матвей продолжил:

– Но вчера, складывая вещи в рюкзак, я заметил, как укладывается шарф под крышкой рюкзака. Она у меня напоминает усечённую пирамиду. Я подумал, что слои большого должны последовательно, без единого пропуска, уместиться в малом кубе целое число раз, чтобы не нарушить принцип симметрии фигуры.

– Ты имеешь ввиду, что слой или несколько слоёв из большого должен уместиться в малом кубе? – уточнила Татьяна. – Но ведь там просто нет свободного места. И вообще, что значит перемещать слои?

– Я предлагаю зафиксировать ребра вложенных друг в друга гиперкубов a, b, c и наполнить всю эту фигуру несжимаемыми гиперкубиками, затем опустошить a-Малый гиперкуб. – Матвей достал несложный чертёж, уже хорошо всем знакомый.