
Полная версия
Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей
Пункт назначения точка P = (10, 10, 20) в координатных осях
При этом подразумевается, что мысленно мы используем оси:
А теперь, допустим, Вы производите запуск с балкона небоскрёба.
Если бы окно находилось по отношению к Вам на 20 м. западнее, на 5 м. южнее и на 15 м. ниже Вашего балкона, то координаты точки P = (-10, -5, -15)
Это так называемая Декартова система координат по имени математика и философа Рене Декарта. Наглядный двумерный случай Декартовой системы координат – это шахматная доска, это плоская карта местности. Каждая точка однозначно определяется двумя координатами.

на Север, на Юг,
на Запад
на Восток
Вниз
Вверх
Запад -Восток – ось Х
Юг- Север – ось Y
Низ-Верх – ось Z
Как бы Вы объяснили двумерному существу?
Как бы Вы объяснили двумерному существу третье измерение – высоту? Предположим, что в совершенно плоском мире Вы ведёте диалог с философом, имеющим богатое творческое воображение, Вы принялись бы объяснять, как можно повернуть ботинок, больше напоминающий в этом случае стельку от обуви, в третьем измерении и сделать из правого ботинка левый и наоборот.
Точно так же трёхмерный ботинок можно разверзнуть в четырехмерном пространстве и сделать правый левым, а левый – правым.
====== Знаете ли Вы что такое Флатландия? ======
=======================================================
Итак, в многомерном пространстве координаты любой точки P задаются относительно начала координат выражением: P = (x, x, … x), а вектор соединяющий начало координат – точку (0, 0,0 … 0) и точку P именуется радиус вектором например A, B, C его компоненты – это координаты по осям: x1, x2, … xn 1 2 n
интересно заметить, что как в двумерном, трёхмерном пространстве, так и многомерном пространстве радиус векторы можно складывать – вычитать покомпонентно:
A + B = (a + b, a + b …. a + b) 1 1 2 2 n n
Так например, в физике происходит сложение перемещений, скоростей либо сил.
А что будет при умножении векторов? Да, такая операция возможна. Познакомимся со скалярным произведением двух векторов, которое происходит также по каждой компоненте отдельно, а результат – число образуемое путем сложения результатов таких произведений:
A * B = a * b + a * b + …. + a * b 1 1 2 2 n n
Попробуем умножить вектор a = (1,1,1) на самого себя
(1,1,1) * (1,1,1) = 1*1 +1 *1 +1 * 1 = 3 или квадрат модуля вектора обозначаемого как |a|. Не принято говорить длина – принято говорить вектора. Легко вычислить, что в n -мерном кубе с ребром a длина наибольшей диагонали равна a * √n в самом деле в квадрате это a * √2 а для случая куба a * √3. 2 вектора модуль
В чём же состоит смысл скалярного произведения?
Например, в физике вектор силы умножить на вектор пройденного путем есть совершенная над телом работа. Если эти вектора со-направлены, то результат будет максимальный, если перпендикулярны, – то нулевой (санки нельзя ускорить, если Вы прикладываете силу поперёк их движения).
======================================================
«Флатла́ндия» (англ. «Flatland: A Romance of Many Dimensions») – роман Эдвина Э. Эбботта, который вышел в свет в 1884 году. Этот научно-фантастический роман считается полезным для людей, изучающих, например, понятия о других пространственных измерениях или гиперпространствах. Как литературное произведение роман ценится из-за сатиры на социальную иерархию викторианского общества. Айзек Азимов в предисловии к одной из многих публикаций романа написал, что это «лучшее введение в способ восприятия измерений, которое может быть найдено».
По этой книге было снято несколько фильмов, в том числе одноимённый художественный фильм 2007 года, в России известный как Плоский Мир.
Глава 2 Удивительный мир симметрии
Вечером на ручных часах Татьяны раздалось бип-бип-бип и появилось сообщение:
Предл. Встрет. завтра 12:00 в «Собачьих бутербродах» у М. Г@ // Борщ. Ок?
Татьяна ответила ОК! и сразу увидела результат голосования других ребят: Матвея и Артура, младшего одиннадцатилетнего брата Татьяны, – все они были согласны. Матвей был самым юным участником творческой группы, представителем той самой , для которой необходимо отыскать доказательство. Если ты сможешь объяснить всё это одиннадцатилетнему школьнику, то будь уверен, сможешь объяснить миллиардам других людей с обычной школьной подготовкой! – убеждала она Матвея. И Матвей хорошо подумав, получив еще раз заверения от сохранении строжайшей конфиденциальности от Татьяны, согласился. целевой группы
Кафе быстрого питания было расположено прямо у выхода метро, напротив университета в этом месте обычно любил назначать встречи Борщов, сопровождая это словами: конечно пища там лишь условно съедобная, но зато место удобное и обстановка уютная, подходящая для диалога.
Он пунктуально пришел на встречу за десять минут до начала и, заняв пустой столик у окна, принялся читать только что изданную коллективную монографию, где наряду с прочими работами была и его: «Социологические методы идентификации судебной коррупции». За окном бурлила предновогодняя жизнь, под аккомпанемент лёгкого пушистого снега и солнышка (вот уже настоящий предновогодний подарок! – отметил про себя Борщов), прохожие и автомобили мелькали в окне, а их полупрозрачные отражения – в самом кафе. Методично раздавался голос кассиров на выдаче:
– Номер восемьдесят пять, один Американо и чизбургер, номер сто четырнадцатый салат из крабов, номер сто одиннадцать: картошка фри…
И вот дружная компания снова собралась за одним столом: Матвей небрежно стаскивал с себя куртку, запорошенную снегом, Татьяна элегантно сняла красивое пальто, которое так эффектно подчёркивало её фигуру. Артур уже сидел в строгом деловом костюмчике, – прямо таки аккуратно причесанный примерны отличник со школьной фотографии.
Матвей заказал кофе, Татьяна и Артур – мороженое, Борщов – чай, который сразу же вылил в раковину и налил себе из бутылочки предусмотрительно купленный в соседнем супермаркете кисло-молочный напиток , бережно извлечённый из профессиорского портфеля: Айран
– А чай все равно не настоящий, робко прокомментировал своё расточительство профессор, пожав при этом плечами – но пустого стаканчика здесь нет.
Ребята обсудили последние новости. Артур сначала держался строго официально, а затем вдруг похвастался последней пятёркой по математике и сказал, что это поможет ему перевестись в лицей, а не оставаться в нынешней прогимназии с . Татьяна чуть укоризненно посмотрела на брата, заметив, что деление людей на и – это дурной тон и снобизм. Матвей смущаясь сообщил, что получил двойку по генетике: потому что к контрольной не готовился, а в генетике много математики, в которой он «немного тугодум», чем вызвал не мало удивления у всей компании. Борщов добавил свою историю о том, как отслужив в армии, он получал двойки на уроках военной подготовки, потому что не мог ходить и стыдился списывать со шпаргалок, а требовалась именно максимальная точность воспроизведения текста. Борщов и ребята много шутили, смеялись, но при этом без насмешек. Наконец, Борщов умолк и лицо его стало серьёзным. лузерами лузеров виннеров чётким строевым шагом
– Сегодня при проведении вебинара, – сказал он, я обнаружил странный эффект. На компьютере запущена программа: то ли Зум (Zoom), то ли Скайп (Skype) – словом, из разряда подобных. Программа просто копирует все что видит в комнате, а также слайды на экране компа и передает по каналам связи собеседникам. За моей спиной проектор отображает эти же слайды на экране. Так вот, надписи слайдов на экране читаются нормально, но те слайды, что за моей спиной на экране – не читаются, поскольку они отражены словно в зеркале.
– Я тоже сталкивалась с подобным, – улыбаясь кивнула Татьяна. – причём, я спрашивала у тех собеседников, с которыми общалась: что Вы видите, можете ли Вы прочитать слайды нормально? – Отвечают, да, всё видим как обычно.
– Вот именно! – продолжал Борщов. – для того, у кого за спиной экран, изображение зеркальное, а для его собеседников – нет. Если оглянуться назад, через плечо, то слайды на большом экране, куда они проецируются, читаются, слайды и презентации на экране компьютера также читаются, а за спиной лектора – отражаются зеркально! В чем здесь фокус?
– На самом деле никакого фокуса нет, – подумав ответил Матвей, просто веб-камера, дисплей компьютера и программа вместе образуют своего рода . Убедитесь в этом, посмотрите на нас вон в то зеркало. электронное зеркало
– Ну и … – недоуменно пожал плечами Борщов, – зеркало, как зеркало.
– Вот именно так все мы привыкли видеть себя в отражении, и поэтому разработчики софта сделали всё таким образом, чтобы потакать нашим привычкам – пояснил Матвей.
– Я предлагаю сделать небольшой эксперимент, сказала Татьяна и начертила на двух салфетках трубочкой от коктейля, измазанной в шоколаде крупные буквы:
– А теперь, Артур, встань за спиной Александра Николаевича с этим транспарантом! – чуть повелительно сказала она своему брату.
Чувствуя значимость порученной миссии, Артур за спиной профессора поднял салфетку.
– Прочитайте, пожалуйста, Александр Николаевич, – обратилась она к Борщову, указывая на зеркало, где отражалось:
– Ад! – прочитал Борщов, глядя в зеркало напротив столика.
– Представьте себе, что это слайды, – продолжала Татьяна. – Вы согласны, что происходит зеркальное отражение?
– Ну это очевидно! Но это почему мои собеседники читают все слайды нормально, а я – нет?
Татьяна жестом показала, что сейчас она всё объяснит и попросила Артура сесть напротив Борщова у свободного столика под зеркалом, держа в руках те же салфетки.
– Теперь снова ДА, прочитал Борщов.
– Александр Николаевич, – пришёл на помощь Матвей, – в мире программирования есть такая функция настройки дисплея, называется (flip) – отразить экран или фотографию. А вообще, программа может представлять изображение как угодно: прямо, зеркально, к верх ногами, под наклоном девяносто градусов и так далее. Но нам привычнее на экране читать тексты слева направо, а своё лицо видеть как в зеркале. Как бы Вы поступили на месте разработчиков сервисов? флип зумпоподобных
– Я бы… постарался сделать эффект полного присутствия – подумав немного ответил Борщов.
– Да, продолжила, Татьяна, поэтому свой текст на экране и своего собеседника мы видим без зеркального отражения, а изображение своей фигуры – как в зеркальном отражении. И всё что у нас за головой, попадающее в поле веб – камеры, мы также видим как в зеркале, посмотрите же на Артура ещё раз!
– Ах, да! – стукнул по своему столу Борщов. – ну какой я тупица! Это же надо, как просто! Коллеги, Вы меня положили на обе лопатки!
Ребята дружно улыбнулись, ещё бы: один гол в их пользу.
– Ну а теперь, я уверен, что с Теоремой Ферма Вы справитесь, – улыбаясь сказал Борщов. Что Вам удалось отыскать?
Матвей достал стопку листов с рисунками и стал пояснять. Он пытался разворачивать текст и рисунки к Борщову, но тот остановил репликой: я читаю вверх ногами без труда.
Матвей не торопясь начал:
– Давайте рассмотрим терему Ферма с позиции физики и геометрии. Именно в этом направлении есть шансы отыскать решение, основные идеи которого можно схематично уместить на достаточно широких полях книги.
Рис. 2.1. Гиперкубы с ребрами a, b и c, вписанные друг в друга с общим центром, совпадающим с началом координат в пространстве размерности 3.
Не меняя общности, можно считать что справедливо неравенство для нашей тройки чисел a На деле оказывается, что таким делителем всегда будет двойка и её степени, а это означает, что исходное предложение относительно числителя и знаменателя оказались ошибочными: оба они чётные, делятся на два, а мы исходно предполагали, что p, q не имеют общих делителей, которые заранее сократили. Матвей говорил, водя карандашом по рисунку: – Предположим, что искомая тройка целых чисел существует. Можно сопоставить ей соответствующую фигуру в виде гиперкубов с ребрами a, b и c, вписанными друг в друга в многомерном пространстве. ….… … … … …… … … … …… … … …… ДА АД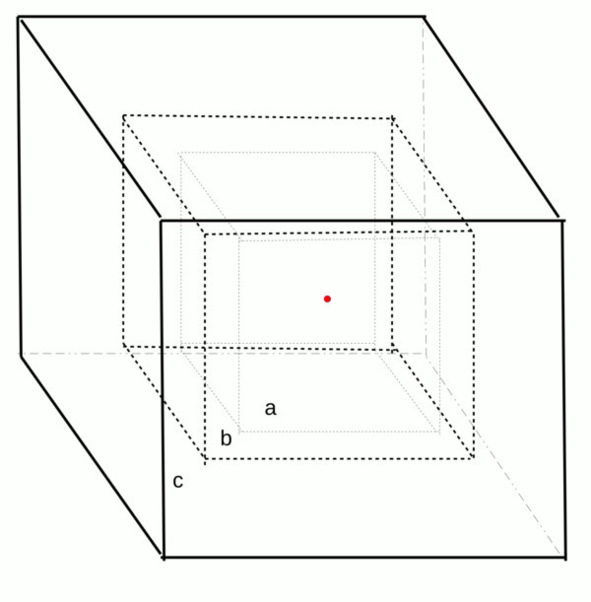
Вкусная коробочка в зазеркалье
Артур закрыл глаза и вспомнил, как накануне вечером Татьяна пригласил его подойти к трильяжу – тройному зеркалу на тумбе. Мама несколько раз порывалась выбросить этот бабушкин антиквариат, но Татьяна отстояла: очень ей нравилось рассматривать свои наряды и прочёску с помощью главного основного и двух боковых поворачивающихся зеркал.
– Ух как вкусно пахнет! – сказал Артур, схватив с тумбочки изящную коробочку из под одеколона.
– Отдай! Я сюда пригласил тебя не для того, чтобы нюхать парфюм – быстро ответил Татьяна и разложила на столе приготовленные для эксперимента предметы. – Смотри что я буду делать внимательно, а лучше снимай на видео.
Татьяна развернула зеркала в одну линию и придвинула коробочку плотно к правому углу главного зеркала. А затем спросила:
– Сколько ты видишь здесь коробочек?
– Ну конечно, две.
– А теперь? – Татьяна повернула к себе под прямым углом правое малое зеркало.
– Теперь четыре – ответил Артур. – Ну это и дураку понятно. В чём фокус?
– Не перебивай и смотри дальше!
Татьяна достала из ящика стола еще одно небольшое зеркало размером с тетрадь и положила его под коробочку.
– Ну, а теперь сколько ты видишь здесь коробочек?
– Раз, два\, три… да их уже стало восемь! – ответил Артур. – Интересно!
– Дальше будет самое интересное, – остановила его Татьяна. – Теперь я нашу коробочку. С этими словами она достала из портфеля квадратные постеры, отсчитала три пачки по десять листочков и принялась ими аккуратно оклеивать переднюю, боковую и верхнюю грани коробочки. утеплю
– Ты как-то плохо утепляешь свой домик – улыбаясь заметил Артур. – у тебя остаются щели.
– Вижу. Сейчас дойдёт очередь и до них.
И Татьяна извлекла из коробка три спички, срезала ножницами серные головки, чтобы не мешали, слегка промазала спички клеем и прикрепила на рёбра утепляемого домика.
– Всё равно остаётся вот эта дырка! – заметил Артур, указав пальцем на верхнюю боковую вершину созданного домика.
– Всему своё черёд – спокойно ответил Татьяна, закрывая эту вершину кусочком красного пластилина размером со спичечную головку. – А теперь скажи, сколько вершин ты видишь?
– Настоящую? Одну.
– Да нет, я не то имела ввиду. Сколько всего вершин ты видишь, не важно настоящие или отражённые?
– Раз, два, три… ну конечно восемь – ответил Артур.
– Вот именно! Каждое зеркало удваивает реальные и отражённые предметы, словно они такие же реальные. Два умножить на два, умножить на два или 2 будет восемь. 3
– Само собой, а где обещанный фокус?
– Фокуса никто не обещал, но он всё-таки здесь есть – улыбаясь ответил Татьяна. – Заметь, всё что я делала с малой коробочкой повторялось в зеркальном отражении. Я оклеила всего три грани: верхнюю, левую боковую и обращенную к нам. И в результате нашей фигуры стали покрытыми. Я прикрепила всего три спички по рёбрам домика – и в итоге нашего домика были закрыты. Наконец, я поместила кусочек пластилина в одну вершину – все восемь вершин оказались аккуратно зарытыми. Тем самым, мы покрыли нашу коробочку . состоящим их трёх граней, трёх ребер и одной вершины. все шесть граней все двенадцать рёбер слоем
– Экономно – задумчиво заметил Артур. Но что всё это значит?
– А это значит, что можно работать с тем представлением, которое нам удобно, но результат будет один. – назидательно сказала Татьяна. – Нам удобно описывать слой в представлении куба или гиперкуба «зажатого в угол» между зеркалами, так проще описывать его математическими формулами. В других ситуациях, нам важно заострить своё внимание на симметричности гиперкуба, совместив его центр с началом координат. Но оба представления легко преобразуются друг в друга. Ты всё аккуратно записал на видео?
– Да
– Значит ты легко убедишься: всё, что ты делаешь с гиперкубом, зажатым в угол между зеркалами, одновременно появляется в зеркальном отражении и наоборот. От наблюдателя можно закрыть основной гиперкуба, те есть нашу коробочку шторкой, но легко представить себе все действия над ним, глядя в зеркальные отражения. Верно?
– Верно.
– А ещё обрати внимание на зеркало. – указала пальцем Татьяна. – Это не просто зеркало а гиперплоскость, в данном эксперименте мы с тобой работали с трёхмерным кубом, зеркало было двумерным, то есть на единицу меньшим пространством. Если бы работали с двумерным квадратом, то все отражения я в таком же порядке произвела бы от двух одномерных прямых, которые, в двумерном мире сыграли бы роль зеркал.
– Угу – ответил Артур.
– Ну раз ты говоришь «угу», то что ты скажешь относительно четырёхмерного пространства?
– Да подумаю… так, так, так -так- так – многозначительно наморщил лоб Артур. Кажется… там был бы особый трильяж с трёхмерными зеркалами, где отразился бы четырёхмерный гиперкуб. Но, убей меня, не могу себе как следует это представить!
– Ничего страшного! – успокоила брата Татьяна, – там гиперплоскости стали бы уже трёхмерными, число отражений стало бы: два умножить на два, умножить … – словом, так четыре произведения двойки, итого 2 или шестнадцать. Столько же стало бы вершин вместе с отражением. Ну и так далее. . . .– Татьяна озабоченно посмотрела на часы. – Детское время кончилось. Всё это нам очень пригодиться завтра на встрече. – подытожила Татьяна. – И не ударь лицом в грязь со своими дурацкими, ненужными вопросами! 4
– Между прочим, я та самая , ради которой «производятся все эти танцы». И мои вопросы вовсе не дурацкие – возразил Артур. целевая группа
….… … … … …… … … … …… … … ……
Пифагоровы тройки на шахматной доске
А тем временем Матвей продолжал:
– Следующие рисунки представляют вписанные друг в друга гиперкубы для случаев размерностей пространства n = 2 то есть плоскости:
Рис. 2.2 Для размерности пространства n = 2, квадраты на плоскости, легко увидеть Пифагорову тройку 3+4=5 2 2 2
– А здесь вершина каждого гиперкуба, выделенного цветом, совпадает с началом координат, в дальнейшем начало координат будет помещаться также в центр гиперкуба. Фигуры в виде композиции гиперкубов начало координат в вершинах и начало координат в центрах гиперкубов преобразуются друг в друга за счет отражения от гиперплоскостей и масштабирования.
Матвей сделал паузу и продемонстрировал на салфетке с пунктирным изображением квадратов, нарисованными трубочкой от коктейля, которую он слегка обмакивал в кофе словно гусиное перо, как легко складывается и раскладывается обратно четыре одинаковых квадрата в разных частях салфетки на рисунке 2.3 выше.
– Обратите внимание, сложить, это все равно, что рассечь фигуру , перпендикулярной определенной оси, или просто прямой для двумерного случая, – прокомментировал Матвей, демонстрируя салфетку на просвет, – ну вот, квадраты почти совпали. Так, совмещаем их центры с началом координат, а грани делаем перпендикулярными каждой из n осей. Теперь можно разложить салфетку, что равносильно операции отражения фигуры от выбранной нами гиперплоскости. Далее Матвей снова, продолжил водить карандашом как указкой по следующему рисунку, комментируя: гиперплоскостью
– Рассмотрим случай целых положительных, т. е. натуральных чисел a, b, c, затем и случай отрицательных чисел. По определению гиперкуб a в n-мерном пространстве это множество точек пространства, удовлетворяющее условию: каждая больше чем минус, но меньше, чем плюс половина ребра гиперкуба: a ½a
– Стоп, перебила Татьяна, – Артур, тебе все понятно?
– Примерно половина сказанного, как-то неуверенно ответил, Артур.
Профессор Борщов одобрительно посмотрел на Татьяну и примирительно сказал:
– Ребята, Вы только что сами убедились, как легко я сел в лужу по простому вопросу отражения в зеркале. Предлагаю, отбросить математический формализм в сторону и говорить на языке школьника 3—4 класса. Ок?
Ну ладно, попробую ещё нагляднее, ответил Матвей, извлекая из портфеля шахматную доску, деревянные детские кубики и маркеры для письма по доске. – эта доска навощена тонким воском, и поэтому на ней можно легко писать вот этими маркерами, затем стирать бесследно и снова писать, я уже пробовал. – На возьми, Артур, обвели три квадрата на шахматной доске размером три на три, четыре на четыре и пять на пять клеток, да при этом начиная с одного и того же места, вот здесь, например, как будто это листы на дереве, растущие из одной точки (см. Рис. 2.2. выше).
Артур легко справился с задачей, он начертил малый синий, затем средний жёлтый и наконец, большой красный квадраты с общей вершиной, примерно так, как на рисунке.
– Можешь ли ты, Артур сосчитать площадь малого, добавить к нему площадь среднего квадрата и сравнить с площадью большого? Артур водя пальцем по шахматной доске начал сосчитал вслух количество квадратов и кивнул: да, действительно девять плюс шестнадцать будет двадцать пять….
– Но ведь это просто теорема Пифагора, – недоуменно сказал он, -мне папа о ней рассказывал, а ещё я слышал, что в честь открытия этой теоремы Пифагор велел заколоть сто быков.
– И с той поры все скоты дрожат, когда открывается новая теорема! – пошутил Борщов.
Матвей охотно продолжил. Он взял в руки детский деревянный кубик и начал окружать его слоем других кубиков, комментируя свои действия словами:
– Представим себе, что я каменщик, что строю дома в многомерном пространстве, но прямо сейчас я работаю в привычном для нас трёхмерном. Я беру единичный кубик, назовем его , беру также цемент или сильный строительный клей и обмазываю тонким слоем каждую грань гиперкубика. В данном трёхмерном случае у меня получается просто куб с ребром три, легко убедиться, что в нём двадцать семь гиперкубиков, то есть элементарных кубиков. гиперкубик
– Всё это ясно, – сказал Артур, а остальные молча кивнули в знак одобрения.
Матвей, сосредоточившись на рисунке, пояснял:
– Пусть образуется путём наслаивания некоторого количества слоёв равной единичной толщины, например один сантиметр или один дециметр, метр – не важно, вокруг , я его буду обозначать его как единичка в степени n или 1, при этом – охватывающий , получается путем добавления например слоёв единичной толщины, c- содержит ещё аналогичных слоёв. В результате уравнение Теоремы Ферма геометрически можно представить образно говоря, как многомерный торт, состоящий из трёх видов слоистых коржей толщиной вложенных друг в друга. a-Малый гиперкуб гиперкубика b Средний гиперкуб a-Малый l Большой гиперкуб m n
– Или просто ящички, ставленные в другие ящички как русская матрёшка – уточнила Татьяна.
– Да – с радостью поддержал её Матвей.
Рис. 2.3. Сечение (пронзание) трёхмерного куба двумерной плоскостью. Между слоями сделан единичной толщины сделан зазор, также равный единице, для наглядности.
– А что такое многомерный куб? – вдруг спросил Матвея Борщов.
– Ах, да! -воскликнул, Матвей, – я должен был это рассказать с самого начала. Он взял чистый лист и стал чертить: Точка, отрезок длиной а, квадрат а, трёх мерный куб а a и т. д. – это гиперкубы соответственно нольмерного, одномерного, двумерного, трёхмерного, четырёх мерного пространства… В этом ряду каждая следующая фигура размерности n образуется путем перемещения гиперкуба размерности n-1 на длину ребра а в направлении, поперечном каждому из n -1 других. 2 3 4 тессеракт
Представьте себе, что мы объясняем двумерному существу, живущему на плоскости, как можно двигаться вверх и вниз. Это конечно, трудно, но например возьмём вот эту прокладку для обуви, – и Матвей как фокусник извлёк из под стола две новые обувные стельки, завёрнутые в полиэтилен, распечатал упаковку.
– Я могу убедить математика, живущего на плоскости, что если бы он смог прибегнуть к помощи трехмерного пространства, то без труда заменил бы левую стельку правой и наоборот. А для нас, трёхмерных существ, так можно было бы поступить с ботинками, а именной взять левый ботинок перевернуть его в четырёхмерном пространстве и получить правый и опять же наоборот из правого -левый!

