Исследование переменных параметров Хаббла

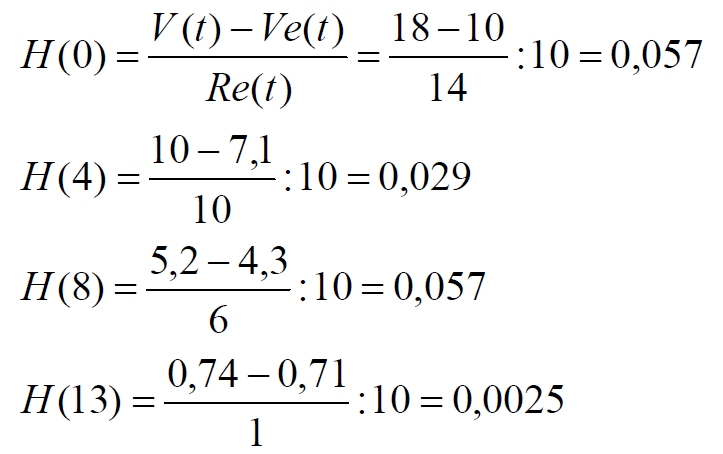
Но является ли в этом случае отношение наблюдаемых величин Vc/Rco реальным значением параметра Хаббла? Вернее, можно ли принять, что мы наблюдаем яркость именно по действительной удалённости источника фотонов Re(t)=Rco и его скорости Vc? Да, дело обстоит именно так.

Момент этот довольно тонкий, поэтому рассмотрим его как можно более детально. Следует признать, что вопрос этот довольно сложный как для восприятия, так и для доказательного изложения. Для его более наглядного рассмотрения нанесём на рис.11.8а несколько дополнительных декоративных элементов: схематичные изображения Земли, сверхновой и фотонов, рис.11.9.

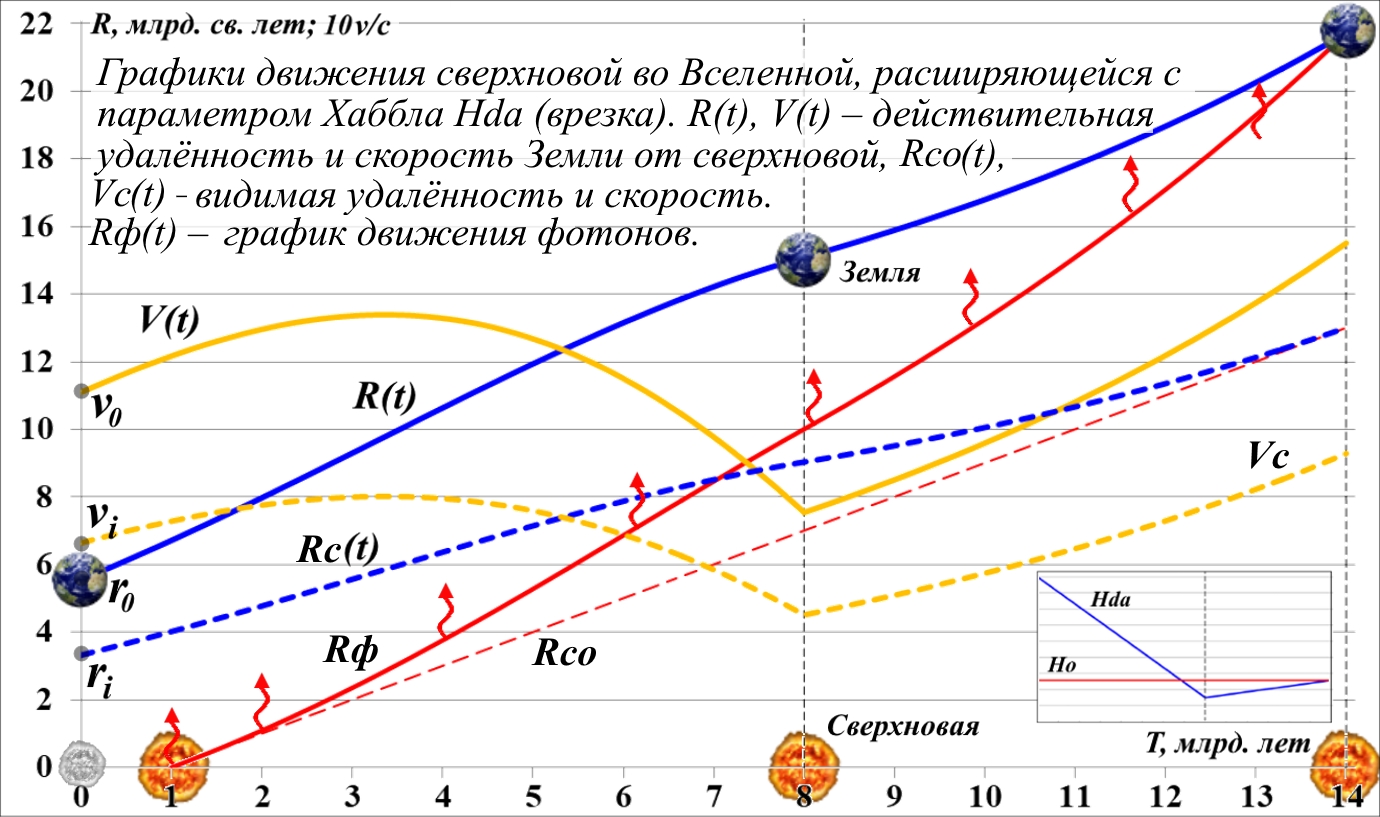
Рис.11.9. Обоснование графиков движения действительного "источника" фотонов.

На рисунке показано, что в начальный момент времени, в момент начала расширения Вселенной t = 0 звезда, готовая стать сверхновой, и Земля находятся в точках с координатами 0 и r0 ~ 5,6 млрд. световых лет. В этом положении звезда изображена приглушённым серым цветом – она ещё не вспыхнула. Поскольку параметр Хаббла Hda в этот момент не равен нулю, Земля имеет начальную скорость относительно звезды (и, соответственно, наоборот), уже превышающую скорость света: v0 ~ 1,1c. Синяя линия, график R(t) показывает текущую удалённость Земли от сверхновой, а линия V(t) горчичного цвета – скорость этого удаления в каждый момент времени. Как видим, в наши дни с этим условным параметром Хаббла Hda расстояние между Землёй и рассматриваемой сверхновой равно почти 22 млрд. световых лет, а их относительная скорость превышает скорость света в 1,5 раза.

В рассматриваемом примере через 1 млрд. лет после начала расширения Вселенной звезда вспыхнула, превратившись в сверхновую. На рисунке в этой точке пространства звезда обозначена теперь уже красно-жёлтым всполохом. Красные волнистые короткие линии со стрелками изображают в каждый момент времени положение одной и той же группы фотонов, испущенных сверхновой. График их движения изображён красной линией Rф удалённости от сверхновой. Отметим, что реальная скорость удаления фотонов от сверхновой превышает скорость света, и в момент прихода к Земле составляет почти 2,5 скорости света. Это не противоречит положениям специальной теории относительности, поскольку, как это традиционно трактуется, "разбегание" Земли и сверхновой не является движением физическим, это кажущееся движение, вызванное расширением пространства между ними.

Противоречие заключается в другом. В момент получения фотонов на Земле они удаляются от своего физического источника, от сверхновой со сверхсветовой скоростью v > c = 1. Из этого следует, что уравнения для эффекта Доплера применить мы не можем. Невозможно подставить в уравнение скорость, превышающую скорость света, поскольку под корнем появляется отрицательная величина:

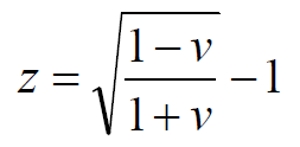
Не существует, наоборот, также и значений красного смещения z, при котором могла быть получена скорость v, превышающая скорость света, поскольку при любом z величина дроби меньше единицы:

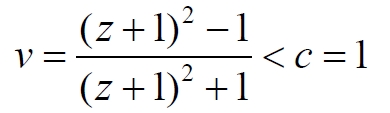
Иначе говоря, мы не имеем права использовать реальную скорость удаления сверхновой от Земли в качестве скорости источника излучения в эффекте Доплера. Поэтому мы не имеем права использовать эту скорость и для определения наблюдаемого параметра Хаббла Hda, поскольку определить скорость v(t) по красному смещению мы не можем физически, следовательно:

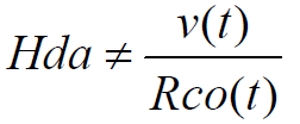
Однако здесь вступает в силу выявленная ранее особенность движения фотонов в расширяющемся пространстве. Поскольку пространство расширяется не только перед фотонами, но и позади них, реальный пройденный фотонами путь от сверхновой до Земли меньше, чем конечное расстояние между последними. Следовательно, красный график движения фотонов Rф(t) не является реальным графиком их движения, он не отражается действительной, физической протяжённости, длины пути, пройденного фотонами.

Как мы определили в предыдущих разделах, действительным графиком пути является светоподобная линия, график Rco. Следовательно, в момент получения на Земле фотонов от сверхновой они прошли меньший путь. В случае рис.11.9 он составил не 21,5 млрд., а только 13 млрд. световых лет, как указывает конечная точка графика Rco.

С другой стороны, это означает также, что за 13 млрд. лет, времени расширения пространства с момента вспышки сверхновой, в точку встречи "прибыл" и получатель фотонов – Земля. Другими словами, до точки встречи с Землёй фотоны прошли путь 13 млрд. световых лет. Но это также означает, что фактический, реальный источник фотонов в момент излучения находился теперь уже не в точке нахождения сверхновой, а на таком же удалении от Земли.

Если трактовать ситуацию буквально, то с момента этой реальной "вспышки", начала движения фотонов, Земля двигалась 13 млрд. лет и прошла от источника фотонов этот самый путь – 13 млрд. световых лет. Ввиду изотропности Вселенной, все эти 13 млрд. световых лет Земля двигалась с параметром Хаббла Hda, точно так же, как и реальный, фактический источник фотонов удалялся от неё с этим же параметром. Развернув течение времени в обратную сторону, мы можем по конечному значению взаимной удалённости определить и начальную точку ri в пространстве этого источника фотонов в момент времени t = 0. Нужно всё-таки понимать, что на самом деле это некий фиктивный, не физический источник, он даже не совпадает в пространстве с местоположением сверхновой. Его появление и проявление связано не с физическим движением участников, а с движением вследствие расширения пространства.

Итог такой инверсии времени показан на рис.11.9. Обращаем внимание, что фиктивный источник в момент времени t = 0 фотонов не испускал. Как видно на рисунке, на момент начала расширения пространства источник находится не в точке вспышки ri ~ 3,5, а в точке, удалённой от сверхновой на 4 млрд. световых лет. Именно от этой точки фотоны и начали свой путь к Земле длительностью 13 млрд. лет.

Выглядит, конечно, весьма странно: источник фотонов не совпадает со сверхновой в момент её вспышки. Ещё раз подчеркнём это важное обстоятельство. В момент начала пути от указанного источника фотон "видит вдали" силуэт Земли. Земля непрерывно удаляется от фотона, но при встрече с нею одометр (измеритель пути) фотона покажет именно дистанцию Rco = 13, пройденную им за эти годы. Инверсия времени в пути (13 млрд. лет) даст нам начальную удалённость источника от Земли, а инверсия всего времени от начала расширения Вселенной (14 млрд. лет) даст нам удалённость этого же фиктивного источника от сверхновой ri, что хорошо видно на рис.11.9. Но и эта точка, и точка испускания фотонов лежат на одной и той же кривой – на Rc(t). Следовательно, первая из них за 14 млрд. лет, а вторая за 13 млрд. лет придут в одну и ту же конечную точку пространства: на рис.11.9 это 13 млрд. световых лет. Ещё раз, выглядит это, несомненно, довольно странно: к моменту встречи с Землёй фотоны прошли путь до неё такой же, на какой они удалились от источника – сверхновой, но при этом Земля оказалась от сверхновой на существенно большем реальном удалении – 21,5 млрд. св. лет.

Из этого странного, но строго логичного обстоятельства и следует главный вывод. Поскольку нам известна начальная удалённость ri источника от сверхновой, источника фиктивного, но ставшего впоследствии, через 1 млрд. лет реальным, мы в изотропной Вселенной можем вычислить также и vi – скорость удаления источника от сверхновой. Но фотоны, в конце концов, достигли Земли, следовательно, в этот момент эта скорость vi является также и скоростью Земли относительно источника фотонов – сверхновой, поскольку их движение описывается теми же уравнениями расширения пространства, но за более короткий период.

Здесь следует признаться, что приведённые рассуждения кажутся нам всё-таки довольно сложными и выглядящими недостаточно полными, убедительными, поэтому приведём дополнительные пояснения.

Наши вычисления о пройденном фотонами пути относятся к системе отсчёта, которую можно называть фиктивной системой отсчёта источника. Можно сказать иначе: к системе отсчёта фиктивного источника. В этой системе учитывается путь, пространство, удлиняющиеся только перед движущимся фотоном. Следовательно, в момент встречи фотона с Землёй оба они находятся на реальном удалении от источника, равном пути, пройденному фотоном, в данном случае – 13 млрд. световых лет.

Исходя из этого, эквивалентно получается, что это именно Земля удалилась от источника в результате расширения пространства с соответствующим параметром Хаббла – H(t). Следовательно, в момент получения фотона на Земле она приобретёт скорость, отвечающую этому движению, то есть скорость приёмника относительно источника, используемую в расчётах эффекта Доплера. Особо отметим, что это не приращение скорости Земли, приёмника, а её абсолютное значение относительно источника. Действительно, в момент "отправки" фотона от источника их начальные скорости равны, поэтому их можно принять равными нулю. В момент "встречи" с Землёй область пространства с фотоном, приёмник имеет отмеченную абсолютную скорость относительно её положения в момент излучения.

Исходя из этого, мы имеем все основания произвести ретроспективу времени и найти условное начальное положение Земли относительно источника, как эквивалент начального положения движущейся области с фотоном. Для удобства, удобства графического изображения находим положение области в момент начала расширения Вселенной, то есть, не 13, а 14 млрд. лет назад – ri. Это допустимо, поскольку обе эти точки находятся на одном графике. Теперь мы можем найти и скорость Земли в момент наибольшего её удаления от источника, в наши дни – Vc(14), в момент получения фотона. Ещё раз отметим, что на самом деле от источника удалялся "доплеровский приёмник", а не Земля, которая в конце просто оказалась в нужной точке.

Диаграммы для действительных источников

Исходя из этих данных, наблюдаемые диаграммы Хаббла рис.11.3 и рис.11.5 также приобретут иной вид, вид, который соответствует действительным источникам фотонов – вид прямолинейной теоретической диаграммы Хаббла R(v) на рис.11.3.

В этом случае получается, что даже на основе наблюдаемых параметров сверхновых мы будет получать одну и ту же связку скорость-яркость любой сверхновой, одну и ту же, как для равномерно расширяющейся Вселенной, так и расширяющейся ускоренно или замедленно.

Как видно на рис.11.8абв, для сверхновой, вспыхнувшей 14, 10 или 6 млрд. лет назад мы получаем одно и то же значение параметра Хаббла:

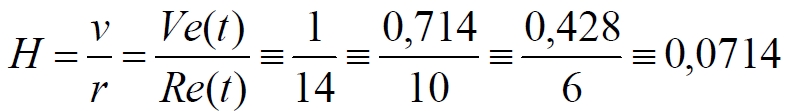
Буквально это означает, что при таком подходе никакие реальные наблюдения не позволяют нам определить предысторию расширения Вселенной, как она расширялась в прошлом. Однако эти же тождества сразу же поднимают серьёзный вопрос. Они никак не проясняют, почему дальние сверхновые видны более тусклыми, чем это следует из стандартной линейной диаграммы Хаббла, в том числе и из полученных здесь новых диаграмм. На каждой из них, для соответствующего значения параметра Хаббла, точки каждого единичного наблюдения неизбежно должны ложиться на стандартную прямолинейную диаграмму. Никакой пониженной яркости при этом возникнуть не может.

Однако астрономические наблюдения показывают, что дальние сверхновые всё-таки менее яркие. Для объяснения этой пониженной яркости можно сделать достаточно разумное предположение. В процессе движения потока фотонов пространство испытывает помимо продольного расширения также и поперечное. Совершенно очевидно, что удлиняется не только волна излучения, но и расстояние между соседними волнами в пучке света.

Как известно, угловое расширение светового потока позволяет определить удалённость источника света. Действительно, о реальной удалённости объекта, стандартной свечи мы судим по её яркости, которая в неподвижном пространстве уменьшается обратно пропорционально квадрату расстояния.

В неподвижном пространстве отношение площадей фотонных потоков прямо пропорционально квадратам их удалённостей. Но в расширяющемся пространстве эта квадратичная пропорция нарушается, поскольку площадь сечения потока в процессе удаления увеличивается за счёт расширения пространства. Яркость же обратно пропорциональна площади потока, поэтому в расширяющемся пространстве источник виден тем более тусклым по сравнению с квадратичной зависимостью, чем дальше он находится.

Допустим, мы наблюдаем только один фотон, который никакого поперечного хаббловского расширения не имеет. Траекторию такого фотона можно представить как очень длинный пучок прижатых друг к другу струн, трос. Их толщина одна и та же, как в исходной, так и в конечной точках. Определить яркость источника по одному единственному фотону, или по этому пучку "фотонных струн", тросу мы не сможем.

Но если трос расплести, если принять пучок струн-фотонов разбегающимся в стороны, то в наш телескоп попадут тем меньше фотонов, струн или нитей троса, чем дальше от нас их начало. И здесь уже важно, по какому закону эти фотоны удаляются от осевой линии, как резко разлетаются в стороны струны троса. Если траектории фотонов и натянутые струны расходятся, оставаясь прямолинейными, натянутыми, то плотность принятого потока будет одна, обратно квадратичная. Но если по мере удаления расталкивать их в разные стороны принудительно и очень сильно, то плотность принимаемого потока будет существенно ниже. То есть, помимо обычного углового расширения фотонного потока требуется учитывать и его принудительное хаббловское расширение.

Можно эту картину описать и в виде традиционной раздувающейся сферы. В момент вспышки сверхновой от неё начинает удаляться фотонная сфера изначального диаметра. Пусть это будет условный 1 метр. Эта фотонная сфера вблизи сверхновой полностью попадёт в наш телескоп с диаметром входной трубы тоже 1 метр. То есть вблизи от сверхновой мы увидим все эти фотоны полностью, получив максимальную яркость сигнала. Если же телескоп находится на удалении, скажем 100 метров от точки взрыва, то фотонная сфера увеличится в диаметре в соответствии с характером расширения пространства. Следовательно, во входную трубу нашего телескопа попадёт уже меньшее количество фотонов из этой сферы. И этих фотонов будет тем меньше, чем дальше телескоп находится от точки вспышки и чем быстрее сфера раздувается.

Легко догадаться, что диаметр фотонной сферы будет увеличиваться строго по закону расширения пространства, то есть будет иметь, например, значение R(t) рис.11.9. Но мы на диаграммах показываем именно значение R(t), а не площадь принятой части фотонной сферы, которая имеет значение πr2, где r – диаметр входной трубы телескопа. В предыдущих рассуждениях это обстоятельство мы не учитывали. С учётом же этого фактора вывод о невозможности наблюдения скорости расширения или наблюдения ускорения, сделанные выше, выглядят теперь уже не таким убедительными, их следует серьёзно пересмотреть.

Действительно, в случае учёта поперечного хаббловского расширения пространства, даже при линейном законе расширения H0 = const дальние сверхновые будут видны более тусклыми, что приведёт к искривлению даже прямолинейной диаграммы Хаббла, что даже в этом случае может трактоваться как космологическое ускорение.

Более того, независимо от характера расширения Вселенной: равномерного, ускоренного или замедленного, полученные в последних выкладках диаграммы Хаббла R(v) сразу же приобретают вид, отличный от прямолинейного, они искривляются кверху.

Как следствие, такое отличие реально наблюдаемой криволинейной с изгибом вверх диаграммы Хаббла R(v) от классической прямолинейной не может считаться однозначным свидетельством ускоренного расширения Вселенной. То, что наблюдаемая диаграмма Хаббла R(v) изгибается вверх от прямолинейной теоретической диаграммы, может быть следствием поперечного хаббловского расширения светового потока по мере его удаления от источника.

Можно предположить, что при замедленном расширении пространства эта тенденция также будет наблюдаться, но в меньшей степени. То есть, буквально, наблюдаемая диаграмма Хаббла для замедленно расширяющейся Вселенной будет выглядеть так, будто она расширяется ускоренно.

Иначе говоря, по сравнению со Вселенной с параметром H0 все сверхновые будут видны менее яркими. Вероятно, при этом дальняя сверхновая в ускоренной Вселенной будет видна более тусклой, чем в равномерной и замедленной. Однако мы имеем только один реальный набор измерений, сравнить который не с чем, вследствие чего остаётся лишь один определённый вывод: независимо от характера расширения Вселенной дальние сверхновые видны более тусклыми, чем в пространстве, описываемом прямолинейной диаграммой Хаббла. Любые наблюдения должны показать ускоренное расширение, отклонение диаграммы Хаббла R(v) вверх от теоретической, прямолинейной.

Вместе с тем в этом случае открытым остаётся ещё один вопрос: почему сверхдальние сверхновые имеют, наоборот, тенденцию к увеличению яркости. Возможная причина – характер расширения Вселенной в этот сверхдальний период резко, инфляционно ускоренный.

Чтобы немного прояснить эти странности, попробуем определить степень влияния на диаграммы поперечного хаббловского расширения пространства.

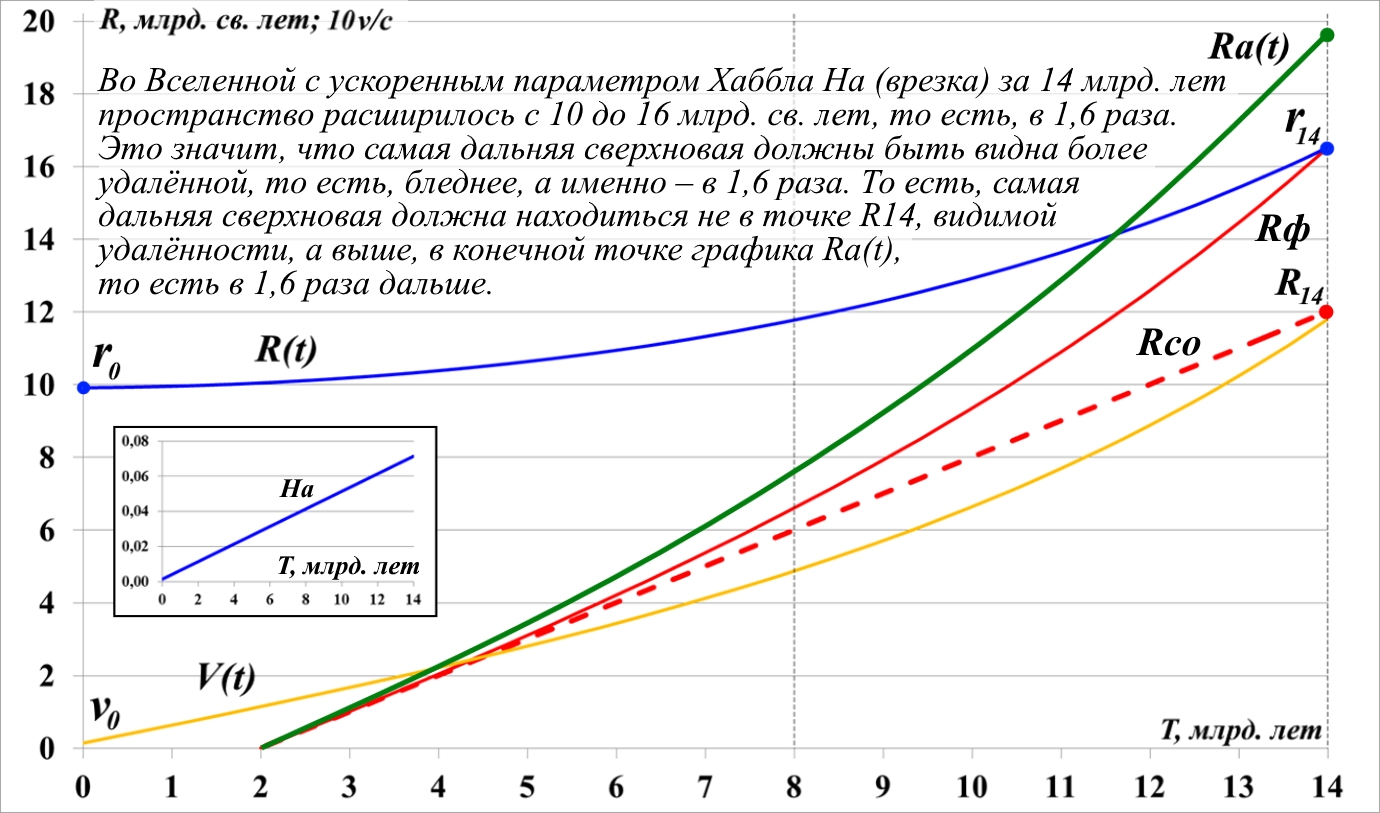
Рис.11.10. Аналитически-графическое представление связи удалённости и яркости светящегося объекта в разных Вселенных

Обратимся к рис.11.10, на котором представлен график ускоренного расширения. За 14 млрд. лет фрагмент пространства расширился с 10 до 16 млрд. св. лет, то есть, в 1,6 раза. Это значит, что самая дальняя сверхновая должны быть видна более удалённой, то есть, бледнее, а именно – в 1,6 раза. То есть, самая дальняя сверхновая на рисунке должна находиться не в конечной точке штрихового графика R14, а выше, в конечной точке графика Ra(t), то есть в 1,6 раза дальше.

Напротив, ближняя сверхновая должна точно совпадать с конечной точкой штрихового графика. Видимо, коэффициент умножения можно выявить из выражения:

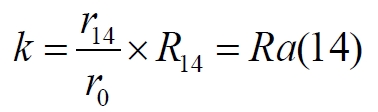
Здесь, r0(t) и r14 – удалённость от сверхновой в момент вспышки t и в момент наблюдения вспышки в наши дни, а R14 – кажущаяся наблюдаемая удалённость сверхновой, вспыхнувшей в момент t. По сути, этот коэффициент и является действительной удалённостью Rk(t) = Ra(t). Проверим по рисунку уравнения на осмысленность. Находим для дальней, ближайшей и самой дальней сверхновых:

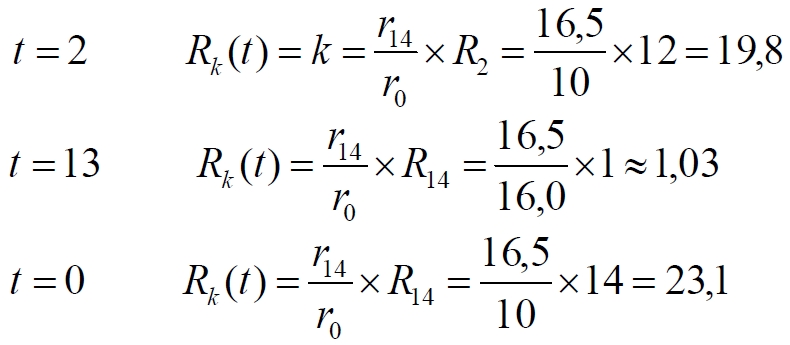
Получается, что самая дальняя сверхновая видна на большем удалении, чем даже она находится на самом деле. Рассмотрев сверхновые с начальной удалённостью 10, но в момент вспышки находящиеся на разных удалённостях от Земли, получаем для них ориентировочно, "на глазок" следующий график значений действительной, реально наблюдаемой удалённости:

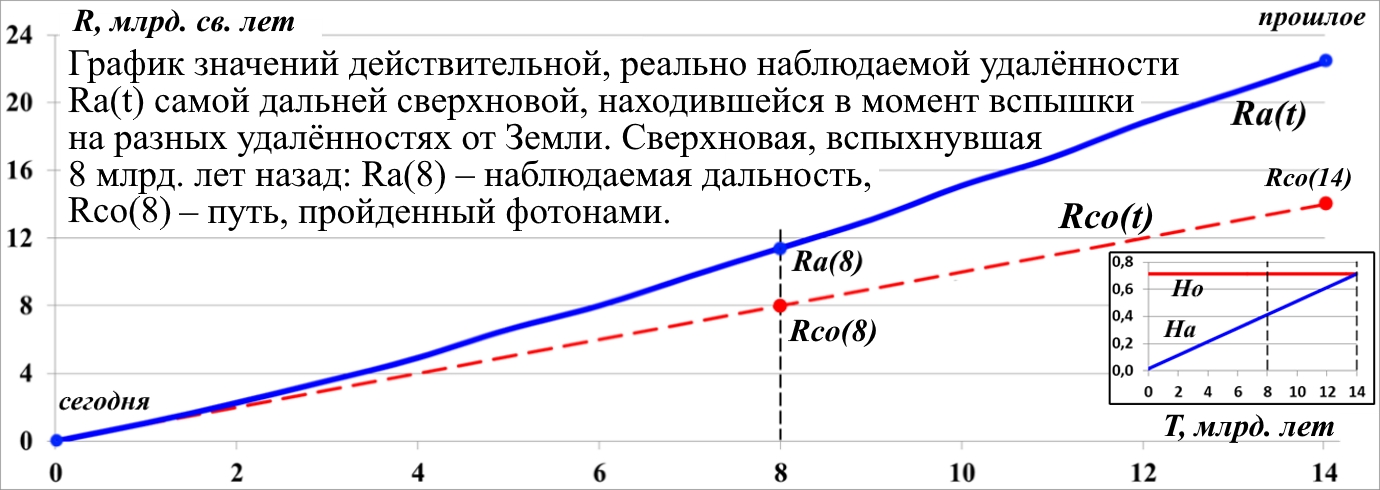
Рис.11.11. График реальной удалённости сверхновой с учётом времени в пути света от вспышки

Чем дальше в прошлом произошла вспышка сверхновой (вправо, время вспышки от наших дней), тем она бледнее. Этот график построен на основе графиков рис.11.10. Из использованного для построений выражения:

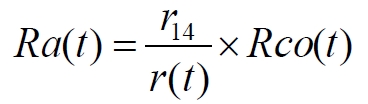
можно определить и величину коэффициента умножения, коэффициента поперечного хаббловского растяжения пространства:

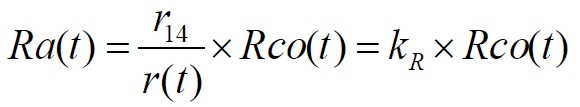
Максимально возможное значение коэффициента, являющегося коэффициентом увеличения удалённости kR = r14/r0 в зависимости от r0 и r14 удобно определить по рисункам рис.11.9 и рис.11.10.

Замечаем, что максимальное значение этого коэффициента зависит только от параметра Хаббла. Коэффициент изменяется от 1 (в наши дни) до максимального значения (в прошлом, 14 млрд. лет назад). Для разных параметров Хаббла, рассмотренных в наших вычислениях, коэффициенты kR имеют максимальные значения:

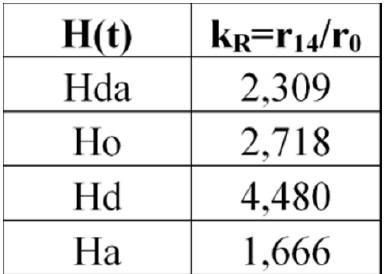
Для сверхновых, вспыхнувших в более позднее время, этот коэффициент уменьшается до единицы в соответствии с законом изменения параметра Хаббла. Обнаруживаем интересную закономерность. Сильнее всего свет дальних сверхновых ослабляется во Вселенной, расширяющейся замедленно, а слабее всего – в ускоряющейся Вселенной.

Параметры H(t) представлены у нас графически и аналитически, поэтому мы можем вычислить максимальные значения kR для Ho, Hd и Ha также и интегрированием соответствующих функций. Например, для Hd:

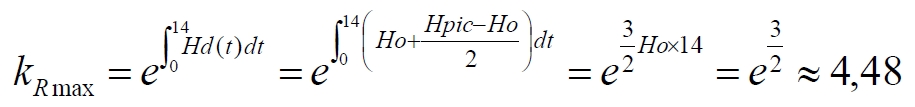
Ожидаем, что обнаруженное соотношение коэффициентов приведёт к интересным следствиям. Для следующих построений используем параметры Хаббла, представленные на врезке к следующему рисунку. Используя их, строим диаграммы Хаббла, учитывающие коэффициент kR для поперечного хаббловского расширения светового потока:

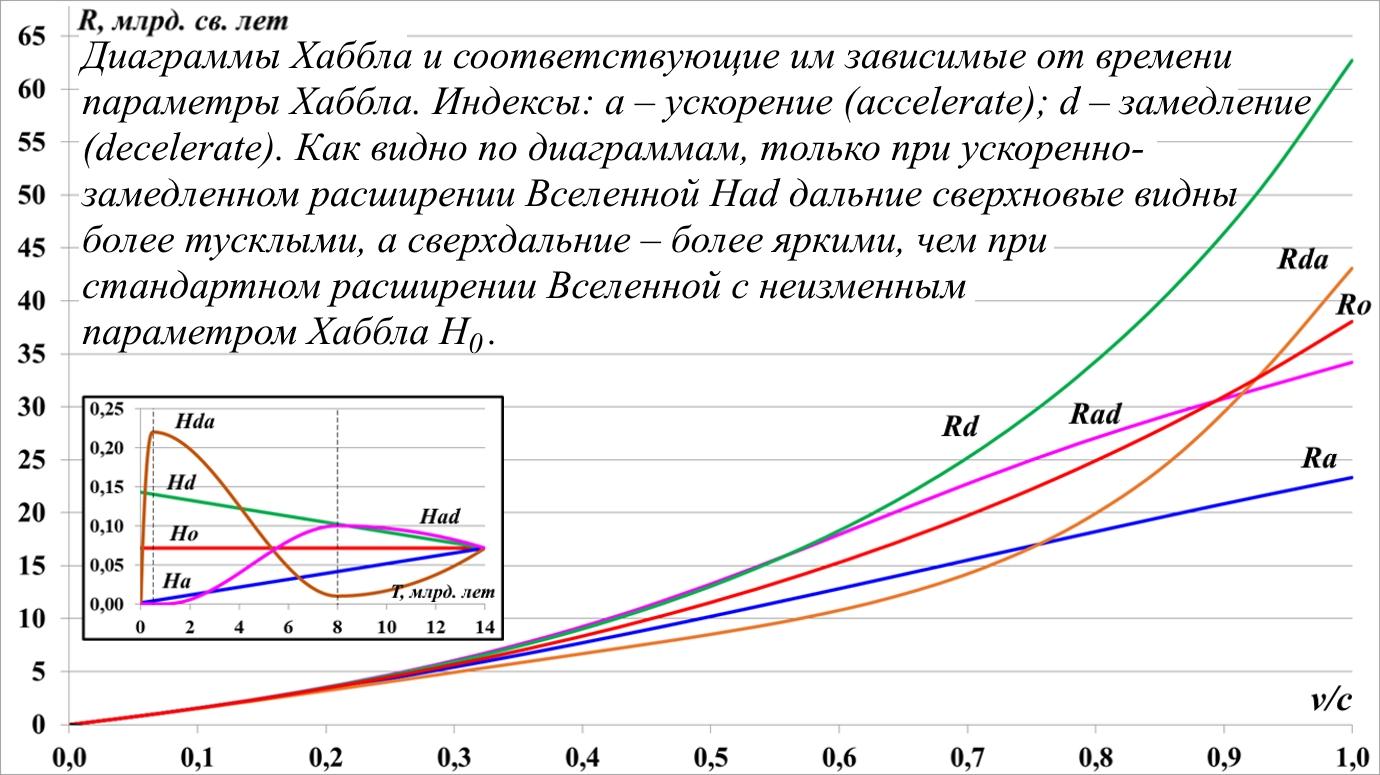
Рис.11.12. Наблюдаемые диаграммы Хаббла с учётом времени в пути света от вспышки сверхновой

В первую очередь на рисунке нас интересует параметр Хаббла Hda, соответствующий принятой модели расширения Вселенной – замедленно, затем ускоренно. При его функциональном проектировании мы исходили из достаточно разумного предположения, что в начальный момент времени этот параметр был равен нулю, после чего он резко увеличился до своего максимального значения, условно через 1 млрд. лет. Далее он уменьшался до момента времени t = 8 млрд. лет, после чего начал расти вплоть до наших дней. Максимальное и минимальное значение параметра – условные.

Обнаруживаем, что, действительно, результат оказался, по меньшей мере, странным. С таким параметром Hda мы не смогли получить диаграмму Хаббла, соответствующую ускоренному расширению. На рис.11.12 видим, что с параметром Hda дальние сверхновые видны более яркими, а сверхдальние, наоборот, менее яркие. Сам параметр Hda определённо соответствует замедленно – ускоренно расширяющейся Вселенной, но производная от него диаграмма Хаббла явно демонстрирует замедленное расширение, если использовать модель "дальний – тусклый". Буквально это означает, что такая модель не является показателем ускоренного расширения.

Но, возможно, другая форма параметра Hda подтвердит эту модель? Этот параметр Хаббла мы спроектировали параметрическим, то есть, его форму мы можем легко изменить, меняя его четыре настроечных параметра: пик и его время и минимум и его время. Простым подбором этих параметров, наугад пытаемся получить такую его зависимость от времени, чтобы характер Hda изменился на противоположный, на ускоренно – замедленный параметр Had, приводящий к известной диаграмме Хаббла, когда дальние сверхновые выглядят более тусклыми, а сверхдальние – более яркими, чем с параметром Хаббла H0.

Такая корректировка прошла успешно и мы получили требуемый инверсный параметр Hda. Строим диаграмму Хаббла на его основе и обнаруживаем, что с такой зависимостью мы получаем известное соотношение: дальние сверхновые теперь видны более тусклыми, а сверхдальние, напротив, со временем замедляют скорость своего разбегания, рис.11.13.

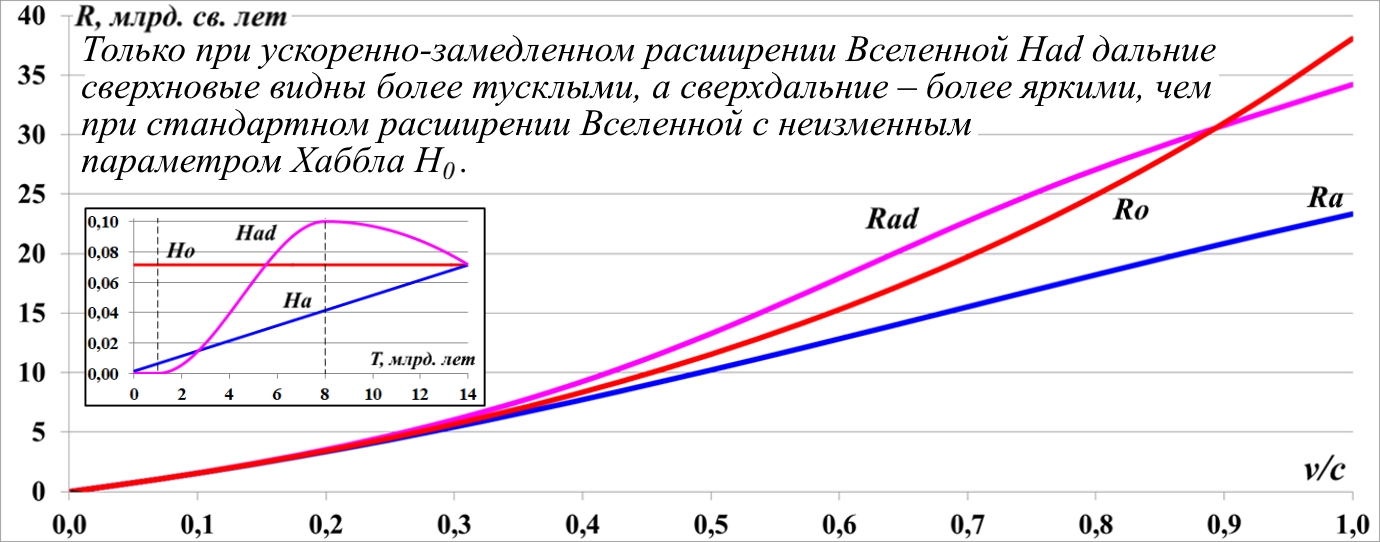
Рис.11.13. Только при ускоренно-замедленном расширении Вселенной с параметром Had дальние сверхновые видны более тусклыми, а сверхдальние – более яркими