Исследование переменных параметров Хаббла

Петр Путенихин

Исследование переменных параметров Хаббла

Введение

Существует предположение, что Вселенная расширяется в наши дни с ускорением, а в более далёком прошлом, напротив, она расширялась замедленно. Какими наблюдениями можно подтвердить это? Считается, что одним из главных аргументов, обосновывающих ускоренное расширение Вселенной, является пониженная яркость дальних сверхновых. Однако это правило выглядит довольно необычно. В самом деле, если они более тусклые, то они находятся дальше, что соответствует скорее их более быстрому удалению в прошлом. Хотя приведённое правило "тусклый-дальний" в целом корректно, правильнее всё-таки говорить, что при ускоренном расширении сверхновые имеют меньшую скорость, меньшее красное смещение, чем этого требует стандартный закон Хаббла. Хотя удалились они на меньшее расстояние, находятся они ближе, чем в равномерно расширяющейся Вселенной. Действительно, несложный анализ показывает, что при ускоренном расширении Вселенной и на самом деле любой объект оказывается на более близком удалении, проходит меньший путь, нежели при замедленном или равномерном расширении.

Давно замечено одно интересное и важное свойство математики – делать верные описания нашего мира, предсказания, на первых порах кажущиеся буквально выдумками:

"… почему математика столь эффективна при описании нашего мира и столь хорошо описывает его эволюцию? … Почему эти правила так хорошо работают?" (Линде)

Вряд ли следует слишком уж сильно этому удивляться. Эта математика так хорошо работает просто потому, что мы и вывели её из прямых наблюдений за окружающей действительностью. Эффективно работает, значит, верно подсмотрели. Более того, в науке и в физике, в частности, уже давно замечена еще одна интересная закономерность: кажущиеся поначалу абстрактными математические выражения, уравнения вдруг оказываются описанием какого-нибудь вполне реального явления:

"… физики обнаруживают, что математические построения, необходимые им для описания нового класса явления, уже исследованы математиками по причинам, не имеющим ничего общего с обсуждаемыми явлениями" (Виленкин).

Однако даже при таком явно полезном подходе следует все-таки быть предельно осторожным при формулировке выводов и следствий из этих математических построений. Можно привести ряд примеров, когда такие выкладки приводят не просто к противоречиям со здравым смыслом, но к довольно заметным противоречиям с логикой, содержат логические ошибки.

В предлагаемой работе мы покажем, что математические выводы в физике во многом зависят как от их последующей трактовки, так и от предположений, оснований, исходных положений, использованных в процессе получения этих выводов. Вообще говоря, это очевидно: если изменить исходные положения, заявить истинными другие, выводы также будут иными, а то и противоположными. Но какие из этих взаимоисключающих выводов верны?

Нас интересуют логические построения, послужившие основой для утверждения об ускоренном расширении Вселенной, опирающиеся на факт пониженной яркости дальних сверхновых. Поскольку детали этой логики нам неизвестны, мы проведём собственные построения, пытаясь прийти к такому же выводу, утверждению.

В дальнейшем мы используем следующую систему обозначений. Все дистанции мы измеряем в миллиардах световых лет, а время – в миллиардах лет. В этом случае скорость света равна единице. Обозначение шкалы скоростей v/c и означает, что значения представлена в долях от скорости света.

У переменных, параметров и графиков нижние индексы состоят из букв и их комбинаций: a – ускорение (accelerate); d – замедление (decelerate); s – условная стационарность, на отдельном участке; о – неизменный, обычный, традиционный. Например, ad – обозначает ускорение – замедление и наоборот. Возможны и более длинные индексы, поскольку некоторые параметры на всём протяжении состоят из нескольких участков: ada – ускорение, замедление, ускорение. Последний индекс – o, по сути, является эквивалентом нуля, используемый просто для удобства записи. То есть, Ho и H0 – это один и тот же параметр Хаббла в нашей Вселенной. Некоторые параметры имеют отдельные обозначения: Rф – график движения фотонов в системе отсчёта сверхновой; Rco – путь, пройденный фотонами по их измерениям; Rc и Vc – графики движения условного источника фотонов, пройденный им путь и его скорость.

Большинство параметров на приводимых диаграммах зависят от времени, однако эту зависимость в их обозначениях для краткости мы чаще всего опускаем.

Все рассмотренные Вселенные и параметры их расширения являются вымышленными, условными и имеют к настоящей, нашей Вселенной лишь качественное, демонстрационное отношение. При этом на одной диаграмме для сопоставления будут изображены параметры движения сразу нескольких Вселенный, никак не связанных друг с другом.

Переменные параметры Хаббла

В основу всех построений, в качестве базового, фундаментального принципа мы положим закон изменения во времени параметра Хаббла. Именно он определяет скорость расширения Вселенной. Скорость его изменения во времени, собственно, и является показателем, эквивалентом ускоренности расширения пространства. Параметр Хаббла неявно, но всегда присутствует на диаграммах Хаббла, зависимости R(v), удалённости некого космологического объекта от скорости его удаления от наблюдателя, Земли. Мы не используем диаграммы Хаббла вида R(z), в частности, по причине их двусмысленности. Связь скорости и красного смещения линейна лишь при малых значениях скорости, однако в литературе очень часто встречаются записи, отождествляющие их даже при больших значениях скоростей: v = cz = z.

Закон Хаббла и соответствующие ему диаграммы можно представить в трёх вариантах. Это: а) теоретический, действительный закон, в реальности – экстраполяционный, б) наблюдаемый и в) условный, для начальных удалённостей объектов. Экстраполяционный характер теоретического закона заключается в том, что эта диаграмма строится на основе наблюдений в ближайшей области пространства, после чего неограниченно продляется.

Определить значение параметра Хаббла в прошлом на основе теоретического закона, видимо, невозможно, поскольку все значения параметров на соответствующей ему (теоретической, действительной) диаграмме относятся к текущему моменту времени, в который параметр Хаббла H0 един для всех объектов во Вселенной. При любом прошлом законе изменения параметра Хаббла теоретическая диаграмма для наших дней всегда имеет один и тот же вид.

Напротив, наблюдаемый закон и наблюдаемая диаграмма Хаббла, вероятно, несут в себе некоторую информацию о величине параметра Хаббла в разные эпохи. Вместе с тем, по этой наблюдаемой величине точное определение его прошлого значение представляет достаточно неочевидную задачу. Рассмотрим, например, следующие три условные варианта изменения параметра Хаббла во времени и соответствующие им три разные Вселенные:

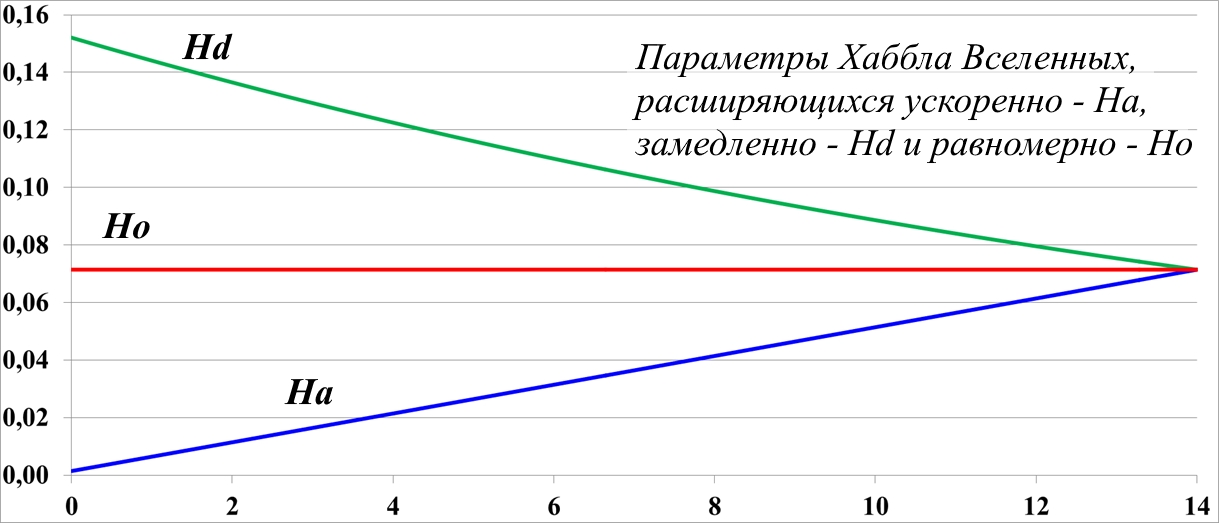
Рис.11.1. Графики изменения во времени параметров Хаббла.

Первый из них, параметр Hd в своей Вселенной убывает от произвольно выбранного значения порядка 2H0 до современного значения H0. Сразу же отметим, что при рассмотрении любого закона изменения параметра Хаббла, его конечное значение обязательно должно быть равно современному значению, поскольку именно это значение мы наблюдаем сегодня в любой из Вселенных. Следовательно, при уменьшении параметра Хаббла во времени, все его прошлые значения определённо могут быть только больше современного. И, наоборот, для возрастающего во времени параметра Хаббла его начальное и все прошлые значения обязательно должны быть меньше современного.

Построим диаграммы Хаббла для расширения Вселенной с каждым из этих параметров, используя выведенный в предыдущих разделах алгоритм определения удалённости объектов с учётом времени в пути света от них до наблюдателей на Земле. Для наглядности изобразим диаграммы с приведёнными на рис.11.1 параметрами на одном рисунке: Ro для равномерно расширяющейся Вселенной с параметром H0; Rd для Вселенной, расширяющейся замедленно с убывающим параметром Хаббла Hd; диаграмму Ra для Вселенной с параметром Ha, возрастающим от некой произвольной малой величины до современного значения, и теоретическую диаграмму Хаббла R(v):

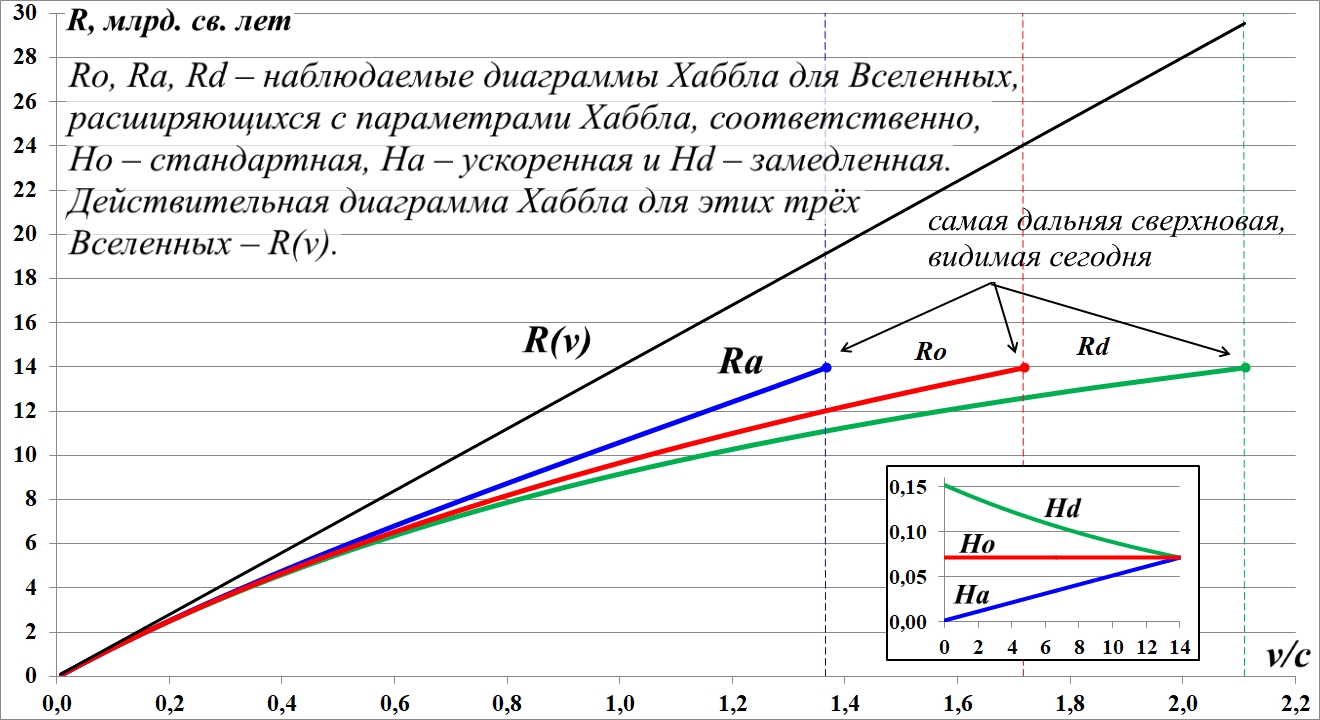
Рис.11.2. Наблюдаемые диаграммы Хаббла для Вселенных с параметрами H0, Hd и Ha.

На рисунке чёрный график R(v) – это слившиеся в один графики теоретического закона Хаббла для Вселенной с H0 и теоретических графиков законов Хаббла для Вселенной с убывающим, Hd и с возрастающим, Ha параметрами Хаббла. Это слияние индивидуальных теоретических графиков Хаббла, собственно говоря, достаточно очевидно, поскольку является следствием того, что в конечной точке, в наши дни все параметры равны H0, и диаграммы соответствуют именно этому моменту времени, когда во всей Вселенной объекты удаляются друг от друга именно с этим параметром Хаббла. При этом отметим некоторую условность: мы принимаем, что скорость источника фотонов равна скорости удаления сверхновой на момент наблюдения фотонов.

Как видим, взаимное положение графиков, диаграмм Хаббла сохранилось, но теперь ни один из них не является прямой линией, как на рис.11.1 и как на стандартной диаграмме. При этом замечаем, что графически при некоторой произвольной скорости сверхновой параметр Хаббла H0 для красного графика больше, чем для зелёного Ha, и меньше, чем для синего Hd. Говоря иначе, график с H0 на рисунке расположен ниже графика с Ha и выше графика Hd:

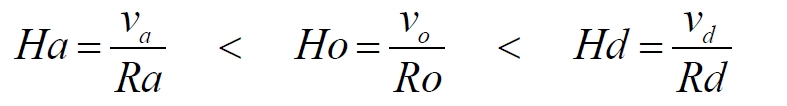
Эти неравенства соответствуют изначально принятым нами условиям. Отмеченные обстоятельства, соотношения мы определённо можем трактовать так, будто при замедленном расширении Вселенной объекты находятся к наблюдателю ближе и, соответственно, видны более яркими. Напротив, при ускоренном расширении Вселенной далёкие галактики, сверхновые видны менее яркими, чем при обычном, равномерном расширении Вселенной, и, тем более, при её замедленном расширении. Иначе говоря, пониженная яркость дальних сверхновых при таком подходе позволяет однозначно идентифицировать, определить ускоренное расширение Вселенной. На рис.11.2 для трёх разных Вселенных представлены только диаграммы Хаббла, поэтому для более детального анализа нанесём на этот рисунок дополнительные графики: времени вспышки и начальной удалённости сверхновых. Штриховые вертикальные линии соответствующего цвета помечают время вспышки самой дальней, самой старой сверхновой для каждой из рассматриваемых Вселенных – 14 млрд. лет назад.

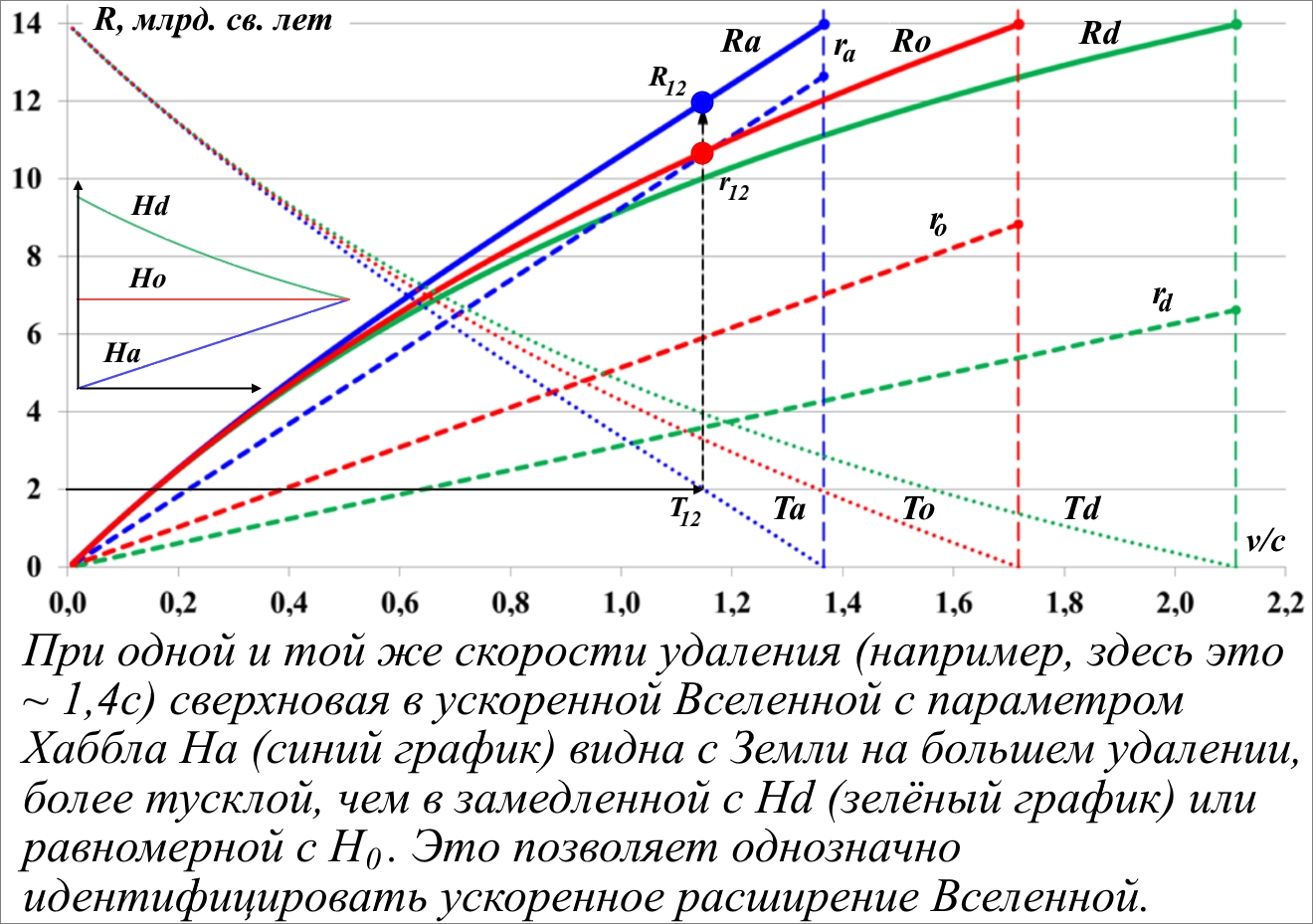
Рис.11.3. Наблюдаемые диаграммы Хаббла, графики времени и начальных удалённостей сверхновых для Вселенных с параметрами H0, Hd и Ha.

Теперь на рисунке можно заметить отмеченную выше небольшую неточность в интерпретации пары параметров яркость-скорость (удалённость), в формулировке "тусклая, поэтому более далёкая". Правильнее всё-таки говорить "яркая, но медленная", то есть, хотя сверхновая более яркая, но движется она медленнее, чем это следует из стандартного закона Хаббла, его диаграммы. Из этого сразу же следует, что с момента вспышки в ускоренно расширяющейся Вселенной сверхновая удалилась на меньшее расстояние и, соответственно, видна более яркой, чем такая же сверхновая в равномерно или замедленно расширяющейся Вселенной. Пониженная яркость ускоренно удаляющейся сверхновой является кажущейся, поскольку вызвана тем, что она изначально находилась на большем удалении от наблюдателя. Малая скорость её удаления и кажущееся большее расстояние до наблюдателя согласно стандартному закону Хаббла вызвана её действительно меньшей скоростью за всю историю движения. А пониженная яркость вызвана её изначально большему удалению.

Действительно, сравним две сверхновые: в ускоренной и равномерной Вселенных, вспыхнувшие в один и тот же момент времени Ta= To= T12= 12 млрд. лет назад. По графикам на рис.11.3 видим, что ускоренная сверхновая в момент вспышки находилась на удалении r12 ~ 10,5 млрд. световых лет, а в момент наблюдения – на удалении R12 = 12 млрд. световых лет. Следовательно, за 12 млрд. лет сверхновая "прошла путь", равный  R12 – r12 ~ 1,5 млрд. световых лет. Соответственно, находим для сверхновой в равномерно расширяющейся Вселенной: r12=6, R12=10,5, откуда R12 – r12 ~ 4,5 млрд. световых лет. В ускоренно расширяющейся Вселенной сверхновая оказалась на большем удалении, поскольку она изначально находилась дальше, хотя и "прошла" меньший путь.

1. Наблюдаемые диаграммы Хаббла

Наблюдаемыми диаграммами мы называем диаграммы, построенные на основе наблюдаемых яркостей и скоростей сверхновых, которые явно зависят от времени в пути света от них. Отметим, что наблюдаемые параметры Хаббла, согласно этим диаграммам, будут отличаться от исходных, действительных параметров, изображённых на рис.11.1. На рис.11.3 каждой точке диаграмм R соответствуют значения скорости и времени, следовательно, мы можем по точкам этих графиков построить и графики H(t)=v(t)/R(t). Но можно использовать и те же таблицы данных, по которым построены эти диаграммы R(v). Правильным способом построения параметров Хаббла в этом случае является дифференциальный, согласно уравнениям:

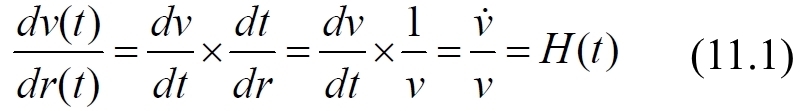
Для построения воспользуемся линиями трендов, позволяющими заменить графические построения аналитическим, на основе уравнений этих линий, что заметно упрощает процедуру. Поскольку у нас есть уравнения R(v), используем первое выражение (11.1), найдя производную R'(v), после чего производим параметрическое построение наблюдаемых параметров H(t), используя v как параметр и учитывая, что H(t)=1/R'(t).

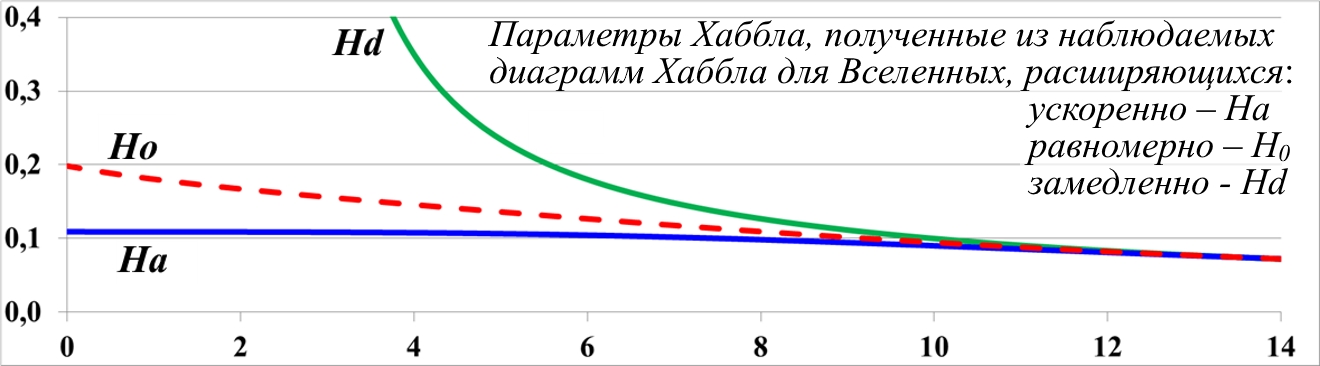
Рис.11.4. Наблюдаемые параметры Хаббла в трёх разных Вселенных.

Обращаем внимание: хотя исходные законы изменени параметров Хаббла разнонаправленны (возрастание, убывание, рис.11.1), наблюдаемые законы их изменения на рис.11.4 все убывающие. Формально это означает замедленное расширение Вселенной, просто с возрастающим параметром Хаббла мы наблюдаем менее быстрое замедление расширения.

2. Параметр Хаббла с изгибом

Проведённые выше исследования, таким образом, согласуются с известным утверждением, что при монотонном изменении параметров Хаббла пониженная яркость дальних сверхновых соответствует более медленному расширению Вселенной в прошлом, то есть, её ускоренному расширению в наши дни. Иначе говоря, монотонное уменьшение или рост параметра Хаббла за время существования Вселенной приводит к соответствующим наблюдательным данным об его уменьшении или росте. Напомним, что рассмотренные монотонные параметры Хаббла условные.

Вместе с тем, пока неясно, что покажут наблюдения при "ломаном" изменении параметра Хаббла: его замедлении с последующим ростом и наоборот.

Для того чтобы выяснить, какими могут быть наблюдения Вселенной с таким ломаным параметром Хаббла, расширявшейся сначала замедленно, а затем ускоренно, вновь спроектируем ещё одну функцию изменения во времени соответствующего параметра Хаббла для некоторой условной Вселенной.

Требуемый параметр Хаббла в простейшем, условном виде скомбинируем из линейных отрезков, исходя из трёх контрольных точек. Первая – это начальное значение параметра Хаббла, вторая – точка изменения направления роста и третья – современное значение параметра.

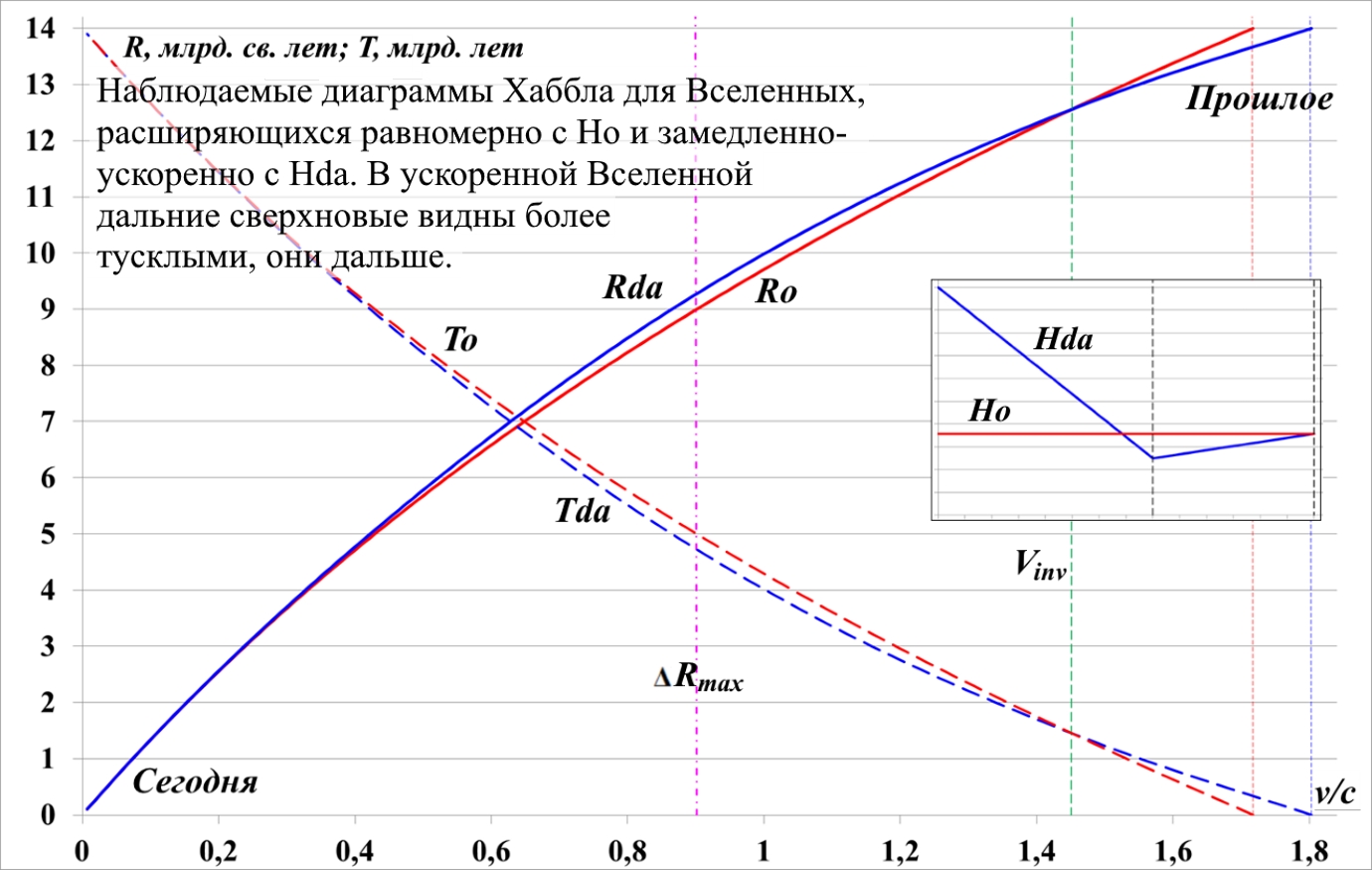
Рис.11.5. Диаграммы Хаббла для Вселенных с H0 (штрих) и Hda. На врезке приведён параметр Хаббла Hda для условной Вселенной, расширяющейся сначала замедленно, затем ускоренно.

Точку излома установим в 8 млрд. лет от начала расширения, поскольку считается, что именно тогда началось ускоренное расширение нашей Вселенной, примерно 6 млрд. лет назад. Один из вариантов такого параметра Хаббла с изломом может иметь, например, вид, представленный на врезке на следующем рисунке. На рис.11.5 приведены диаграммы Хаббла – графики движения R(v) сверхновых в двух разных Вселенных: условной, расширяющейся с указанным параметром Хаббла Hda (замедление – ускорение), и нашей с современным параметром H0. Повторим, что все представленные на рисунке параметры – условные, подобраны по смыслу и не являются реальными данными наблюдений.

Скорость, обозначенная как Vinv ~ 1,45с – это скорость, при которой яркость дальних сверхновых изменяется с повышенной (раньше) на пониженную (позже от начала расширения). Инверсия произошла через 1,5 млрд. лет после начала расширения, что видно по графикам Tо, Tda. Точка ΔRmax – это точка, когда условное расстояние между ускоренной и равномерно удаляющейся сверхновой – максимально. Здесь это ~ 5 млрд. лет от начала расширения, скорость удаления сверхновой ~ 0,9с.

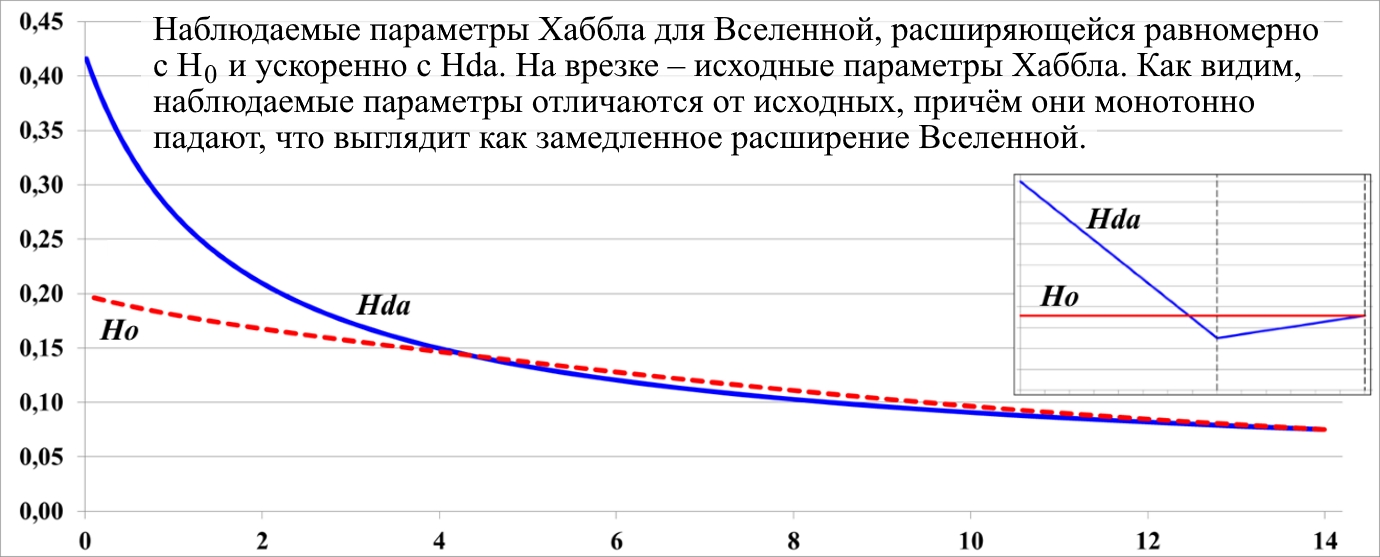
Рис.11.6. Зависимости от времени параметров Хаббла в ускоренной и равномерной Вселенной

На удалённостях ближе 12,5 млрд. световых лет сверхновые видны более тусклыми, они дальше. На ещё большей удалённости – более яркими. Этот момент времени, 12,5 млрд. лет назад для наблюдателя, на графиках является ничем не примечательной точкой, хотя в этот момент замедленное расширение сменилось ускоренным. На удалении 9 млрд. световых лет разница яркости сверхновых максимальна.

Используя рассмотренный выше алгоритм, построим по линиям трендов наблюдаемые графики изменения во времени параметров Хаббла – рис.11.6. Хотя излом, перегиб на рассмотренном параметре Хаббла выглядит несколько неестественно, рассмотренный вариант с его плавным изменением, тем не менее, привёл к графикам, не имеющим принципиальных отличий от рассмотренных.

Отметим это ещё раз явно: рассмотренные параметры Хаббла условно наблюдаемые, то есть, построены на основе вымышленных наблюдений без каких-либо космологических корректировок, без явного учёта времени в пути света от вспышек сверхновых.

На приведённых диаграммах мы видим, что в прошлом ускоренно двигавшиеся дальние сверхновые в наши дни видны более тусклыми. Действительно, их скорости соответствуют большей удалённости. Напротив, ещё более далёкие сверхновые видны более яркими, чем это следовало бы из стандартного закона Хаббла. Однако, на что следует обратить внимание, ближние сверхновые и галактики видны практически неразличимо одинаково яркими, независимо от их скорости в прошлом. Вывод об ускоренном расширении сделан на сопоставлении параметров движения дальних сверхновых с параметрами ближайших к нам. Бесспорно, что вплоть до наших дней Вселенная расширялась ускоренно. Но можно ли утверждать, что и ныне эта тенденция сохранена?

Мы умышленно сформировали такой закон изменения параметра Хаббла рис.11.5, на врезке, что с ним в наши дни Вселенная расширяется ускоренно. Несмотря на это, на рис.11.6 мы видим, что наблюдаемые параметры Хаббла для обоих Вселенных – ниспадающие, отличные от диаграмм на вставке рис.11.5, что формально следовало бы трактовать как замедленное расширение в обоих случаях.

Строго говоря, утверждать ускоренность или замедленность расширения Вселенной следует на основе данных именно по начальному участку диаграмм, по изменению скорости расширения в наши дни. Вместе с тем, на основе полученных достаточно логичных и убедительных результатов мы определённо имеем право вновь повторить сделанный ранее вывод:

Пониженная яркость дальней сверхновой по сравнению с её яркостью в равномерно расширяющейся Вселенной является свидетельством более быстрого расширения Вселенной в настоящее время, начиная со времени порядка 6 млрд. лет назад.

Вместе с тем наблюдаемые законы изменения параметров Хаббла в обоих случаях – ниспадающие. Это выглядит как, наоборот, замедление расширения Вселенной. Кроме того эти ускоренные сверхновые видны на самом деле более яркими, чем они были бы видны во Вселенной с неизменным параметром Хаббла, они к наблюдателю ближе.

3. Проблема сверхсветового движения

Графики движения сверхновых со сформированным выше параметром Хаббла ускоренной Вселенной можно представить в следующем виде:

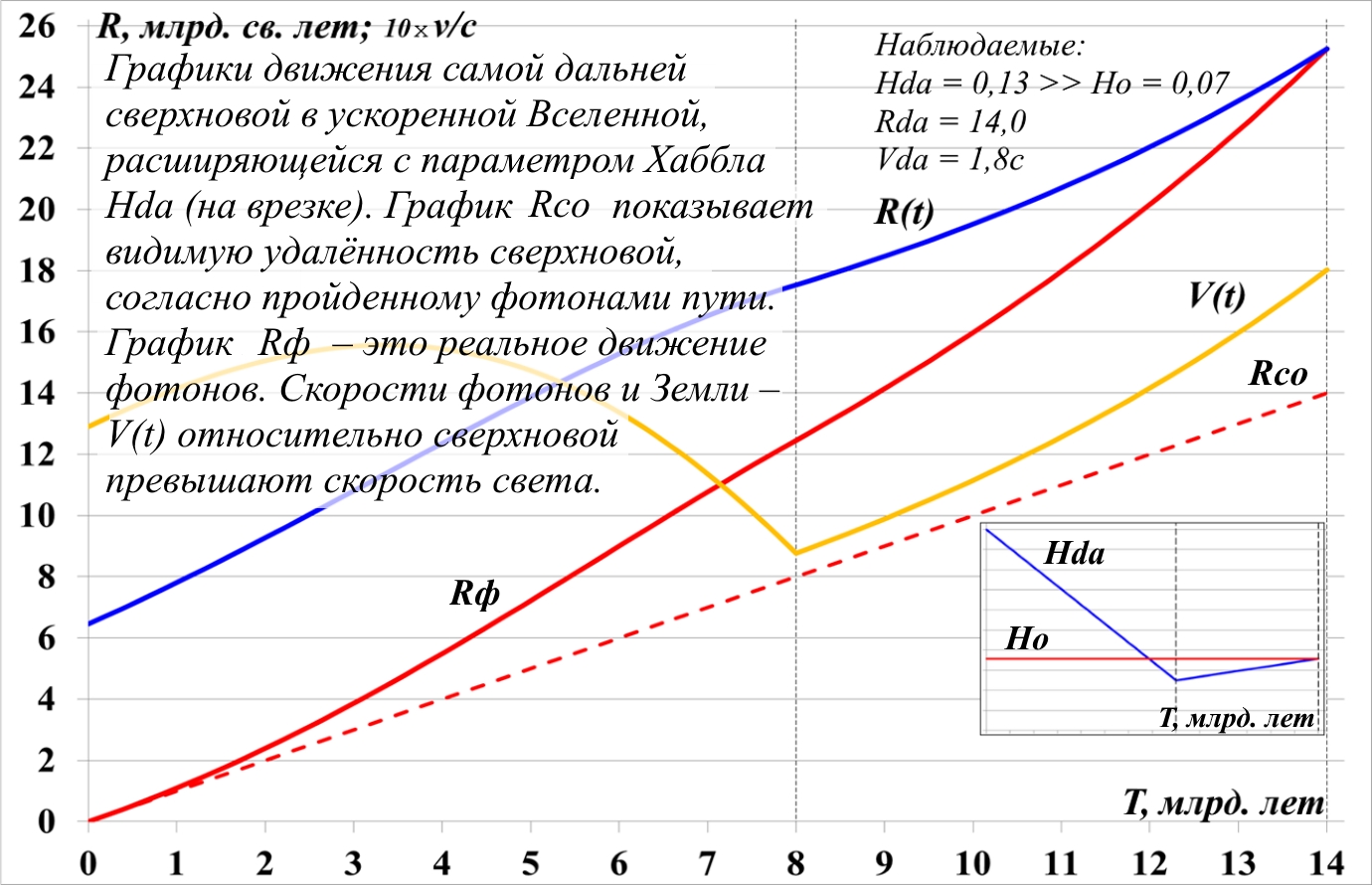
Рис.11.7. Графики движения сверхновой и света от неё в ускоренно расширяющейся Вселенной

На рисунке R(t) – это удалённость по времени сверхновой от Земли (или наоборот). Скорость разбегания сверхновой и Земли – V(t), на рисунке для лучшей видности она увеличена в 10 раз. Графики Rф и Rco – это графики движения фотонов от сверхновой – реальная удалённость и наблюдаемая. На табличке в центре показано, что отношение скорости удаления сверхновой Vda=V(t) к её наблюдаемой удалённости Rco, определяемой по яркости, даёт значение параметра Хаббла Hda = 0,13, что почти в 2 раза превышает значение Ho и явно не соответствует астрономическим наблюдениям.

Кроме этого замечаем, что на рис.11.2, рис.11.3, рис.11.5 и данном, рис.11.7 наблюдаемая скорость удаления галактик превышает скорость света. Однако уравнения для связи скорости и красного смещения такой скорости не допускают. В чём же дело? Мы видим, что фотоны явно достигли наблюдателя – траектории Земли и фотонов, графики R(t) и Rф пересеклись в наши дни, но при этом их физический источник, сверхновая удаляется со скоростью V(t), превышающей скорость света, уравнения для эффекта Доплера неприменимы.

Проблема возникла вследствие того, что мы молчаливо приняли, будто скорость источника фотонов вспышки в момент наблюдения равна скорости удаления наблюдаемой сверхновой в этот же момент.

Однако скорость области пространства, соответствующего удалённости реального источника, соответствующей его наблюдаемой яркости, определённо не равна удалённости галактики. Мы выяснили, что галактика в момент наблюдения фотонов находится существенно дальше, чем путь, пройденный фотонами от неё до наблюдателя. Следовательно, нам следует учитывать не скорость удаляющейся в этот момент галактики, а скорость точки пространства, находящейся на удалении, равном пути, пройденному фотонами.

Согласно разработанным нами уравнениям движения графики движения самой дальней наблюдаемой сверхновой с параметром Хаббла Hda имеют вид рис.11.7.

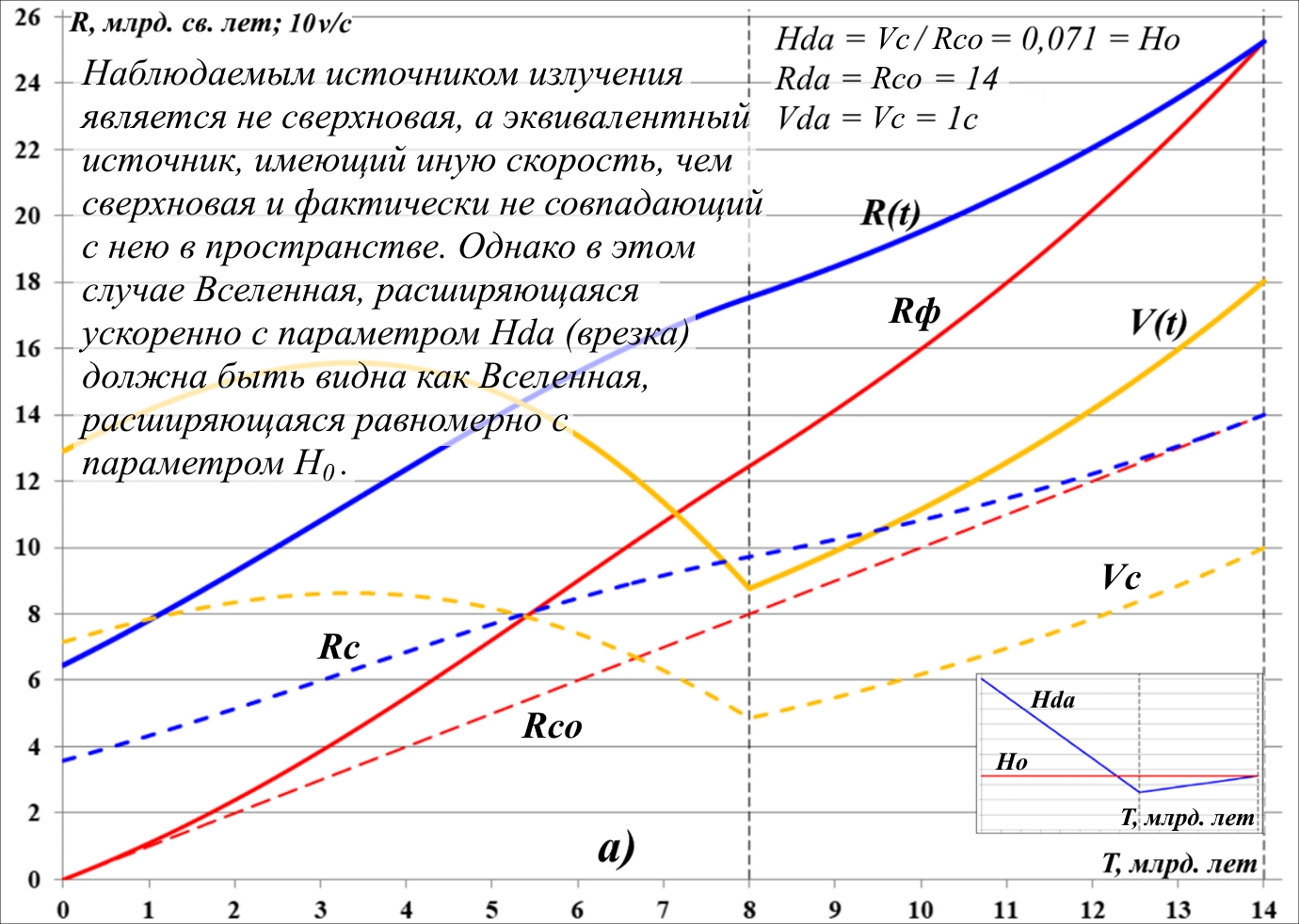
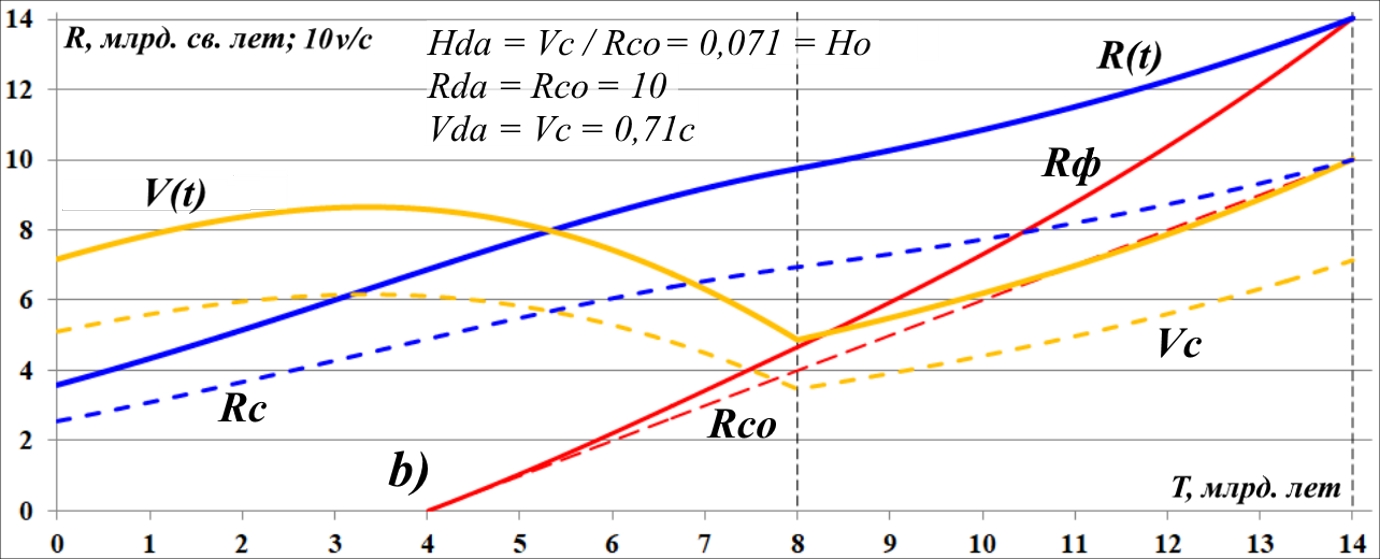
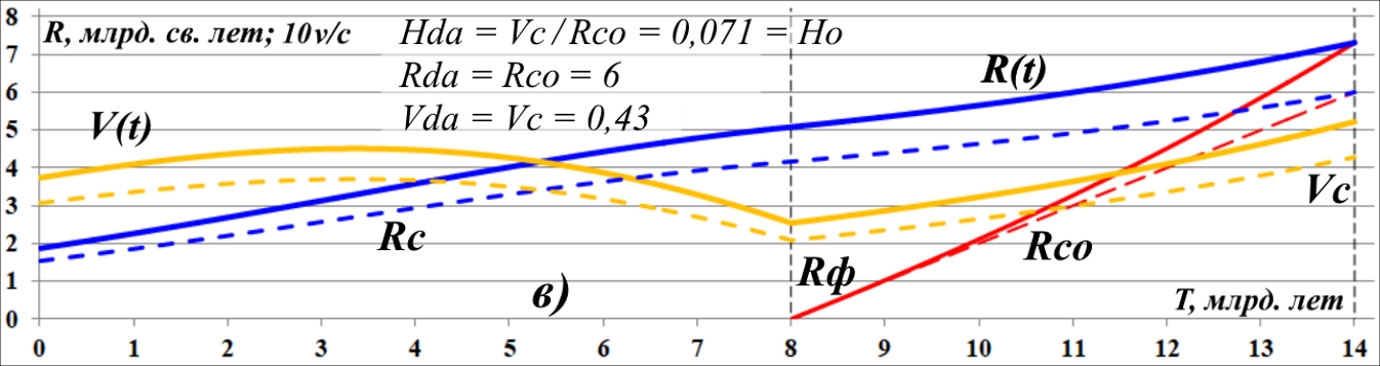
Рис.11.8. Графики движения действительного "источника" фотонов.

Учитывая указанное обстоятельство, на этот рисунок нам следует добавить ещё два графика "дистанция-скорость", как показано на рис.11.8. Согласно этим графикам "исходная" удалённость "действительного" источника фотонов меньше, чем исходная удалённость наблюдаемой сверхновой, а его скорость даже от самой дальней сверхновой теперь уже не превышает скорости света. В этом случае может возникнуть желание определять скорость такого действительного источника фотонов как разность скоростей. Действительно, Земля удаляется от сверхновой со скоростью V(t), а источник фотонов – со скоростью Vc. Следовательно, Земля от источника удаляется вроде бы с разностной скоростью: V(t) – Vc.

Однако, во-первых, наблюдаемой величиной является только Vc, а скорость V(t) для наблюдения недоступна, она сверхсветовая. Во-вторых, такой разностный подход сразу же приводит к труднообъяснимой, даже абсурдной ситуации. При вычислениях наблюдаемый параметр Хаббла Hda в этом случае стремительно уменьшается по мере приближения точки вспышки сверхновой к Земле с 0,06 (самая дальняя сверхновая) до 0,0007 (самая ближняя сверхновая). Как видно на рис.11.8: