Искусство цвета. Цветоведение: теория цветового пространства

Этим новым органом являются колбочки, конические образования, выстилающие изнутри заднюю стенку глаза в центральной ямке, т. е. в том месте глаза, где получаются самые точные изображения, даваемые светом, проникающим сюда через хрусталик. В боковых частях воспринимающего органа, служащих для общего дополнения положения, находится другой, более простой орган — палочки. В глазах вышеупомянутых животных и цветно-слепых людей имеются только палочки. Наблюдения показали, что распознавание и различение цветов происходит только в центральной ямке сетчатки и осуществляется посредством колбочек. В боковых областях своего глаза каждый человек является цветнослепым, т. к. при помощи палочек он различает только светлое и темное[6].

Дальше будет подробно изложено, какому упрощению подвергает наш глаз все колоссальное многообразие попадающего в него света, чтобы видеть цвета, как он их видит. Здесь же мы должны лишь настойчиво подчеркнуть факт существования этого упрощения, факт очень важный для всего учения о цветах.

В свете этих рассуждений можно поставить вопрос: нельзя ли ожидать в будущем еще большего приспособления нашего глаза к многообразию световых лучей? Ответ должен быть решительно утвердительным. Уже теперь мы имеем некоторые признаки этого. Пока, однако, эти успехи настолько слабо выражены, что не имеют практического значения.

Цвета вещей

Если представим себе значительные изменения солнечного света в течение дня с одной стороны, состояние нашего зрительного аппарата: – с другой, и сравним с этими вечно меняющимися условиями зрения, большое постоянство, которое проявляют цвета окружающих нас предметов, то придется с удивлением спросить: каким же образом в итоге действия столь изменчивых факторов получается такой постоянный результат. Это постоянство в действительности создается не нашим зрительным аппаратом, но основывается на другом, чисто физическом явлении, закономерно связанном с нашими ощущениями.

Это физическое явление есть отражение света поверхностями тел. Мы видим, что каждое тело отражает определенную часть падающего на него света. Тело, которое отражает все падающие на него лучи и при этом их рассеивает, называется белым. Из этого не следует, что тело нам кажется белым потому, что оно отражает много света. Белая бумага и в сумерках кажется белой, хотя она отражает очень мало света. Но так как даже и вечером она отражает почти все лучи света, мы называем: ее белой. Чтобы дать правильное определение «белого», мы должны знать, какое имеется в данное время общее освещение; мы должны, следовательно, рассматривать цвет, как явление относительное, соотнесенное. Если исключить эту возможность соотнесения путем смотрения через темную трубку, то мы оказываемся не в состоянии отличить белое от серого.

Отражает ли данная поверхность все лучи света или только часть их, зависит исключительно от ее свойств, но не зависит ни в какой мере ни от освещения, ни от настроенности глаза. Отсюда и происходит постоянство цветов предметов. Так как отражение света есть постоянная величина, которая не зависит от силы света, – всегда отражается определенная доля падающего света, будь то свет сильный или слабый, – мы и видим один и тот же цвет белым, вне зависимости от силы освещения. При этом нам становится ясной и важность закона Фехнера, по которому мы ощущаем отношения, но не абсолютные величины.

На таких же точно основаниях мы называем черной поверхность, у которой отражение света равно нулю. Серая поверхность есть такая, которая отражает одинаковые доли всех лучей спектра. Цветная же поверхность отражает различные доли различных световых лучей.

Во всех случаях отражение света зависит исключительно от тела, которому принадлежит данная поверхность и ни в какой мере не зависит от других причин. По привычке, в результате опыта, мы связываем эти отражательные свойства с нашими ощущениями. Насколько сильна эта привычка, мы видим из опыта Геринга, описанного выше, в главе первой. Можно прекрасно знать, что нижняя бумага белая и что в отверстии нет никакой серой поверхности, и все-таки мы воспринимаем ее как серую. Уменьшив верхний картон настолько, чтоб он был немного больше отверстия и увеличив нижнюю бумагу настолько, чтоб ее можно было видеть выступающей из-за картона со всех сторон, – мы заметим, что цвет отверстия сблизится с цветом всей бумаги, и покажется нам белым. Существует среднее положение, при котором можно видеть отверстие белым или серым в зависимости от направления внимания.

Вышеизложенные рассуждения имеют основоположное значение для измерительного отдела науки о цветах. Если бы отсутствовало постоянство коэффициента отражения (Remission), мы не имели бы величины, достаточно устойчивой для того, чтобы сделать возможными числовые определения. То субъективно изменчивое, что присуще существу цвета, регулируется отношением к этой объективной величине (отражению). И усовершенствование нашей способности распознавать верно цвета зависит и в общем, и у каждого отдельного лица непосредственно от того, насколько определенно и уверенно данный человек согласует свои ощущения с постоянными величинами отражения. При ежедневном опыте мы приобретаем в этом большую уверенность и без научной какой-либо подготовки. Только при совсем необычайном освещении (например, при свете пламени натрия) способность подобного приспособления расстраивается.

Глава IV

Ахроматические цвета

Общее. Эта генетически наиболее древняя область мира цветов еще и теперь занимает обособленное положение, сперва выделившись в особую замкнутую и более простую группу, впоследствии же оказавшись основной осью всей системы цветов. Мы обозначаем всю эту группу цветов, которая простирается от белого к черному через серый, как ахроматические цвета (unbunten Farben).

То, что мы и этого рода зрительные восприятия включаем в понятие цвета, не есть нечто произвольное, а вполне логически обосновано. Вначале думали, что белый, серый и черный цвета такие же обособленные элементы видимого, как и зеленый, красный и синий. Но впоследствии оказалось, что они всегда входят в состав всех цветов, имеющихся в окружающем нас мире вещей. Если бы мы отказались от включения этих цветов в общее понятие цвета, то это привело бы к неимоверным трудностям и противоречиям. Во все времена живописцы и красильщики, художники и маляры, не задумываясь, называли их цветами. Со времен Древней Греции, где черный и белый цвет были единственными, наряду с красным и желтым, и по сей день, эти два цвета на палитре и в красильном чану играют такую же роль, как и хроматические цвета. Отрицание их цветовой самостоятельности не исходит от знатоков этих явлений, а принадлежит философам, которые за черным, как понятием отрицательным (отсутствие света), не хотели признать самостоятельности. Но нужно только рассмотреть это явление с позитивной точки зрения и представить себе черный цвет, как полное лучепоглощение, чтобы устранить это недоразумение.

Таким образом, мы и будем рассматривать и изучать группу белого, серого и черного цветов, как самостоятельную и важную область мира цветов. Историческое первенство этих цветов находит свое отражение в том, что они занимают центральное место и входят во все ощущаемые нами цвета. То, что раньше не сознавали этого, было одной из основных причин, почему наука о цветах, начиная с Гельмгольца, так мало продвинулась вперед в сравнении с другими отраслями знания.

Происхождение ахроматических цветов

Мы воспринимаем как ахроматические те световые лучи, которые имеют тот же состав, что и солнечный свет, или исходящий из того же источника рассеянный дневной свет. Хотя состав дневного света постоянно меняется (как, например: при чистом небе он содержит гораздо больше синего, чем при пасмурной погоде), мы обладаем очень слабой чувствительностью к этим изменениям. Только к вечеру, когда желтые и красные лучи света особенно превалируют, благодаря лучепоглощению в воздухе, мы это «теплое» освещение воспринимаем, как нечто особенное.

Тот загадочный факт, что смеси лучей света различных чисел колебаний и различной длины волны мы воспринимаем, как простое ощущение белого или серого цвета, неоднократно, со времен Ньютона, привлекал к себе внимание. Гёте находил это настолько противоречивым и трудно допустимым, что отрицал анализ Ньютона и утверждал, что дневной свет объективно так же прост, как просто субъективное ощущение белого цвета. Гельмгольц указал на резкое различие между смесью звуковых тонов разной высоты и смесью световых лучей разных цветов. В первой смеси наше ухо может различать каждый тон в отдельности, во второй же глаз наш не способен видеть отдельно составляющие цвета. Объяснения этому противоречию он, однако, не дал. Также и Шопенгауэр, с его теорией качественного деления сетчатой оболочки глаза, не дал нам основных положений для чего-либо, что помогло бы нам психологически объяснить это явление.

Только генетическая точка зрения дает нам такое объяснение. Выше мы видели, что примитивный глаз не воспринимает ничего, кроме различий между сильным и слабым светом. Ступени развития глаза отличаются именно тем, что он постепенно начинает воспринимать разнородность света. Было время, когда ни одно живое существо не было способно воспринимать отличий в числе колебаний, – того, что мы теперь называем цветом. И современный наш глаз еще сохранил многие особенности этого состояния. Самая важная из них та, что и теперь мы всю массу световых лучей ощущаем как цвета: белый, серый и черный. Только представив себе это явление, как пережиток первобытного состояния, вместо того, чтобы рассматривать представление об ахроматических цветах как систематический результат нашего знакомства с хроматическими – как это еще и теперь непроизвольно случается с некоторыми – мы освобождаемся от всех трудностей.

Мы и по сей день обладаем аппаратом палочек в нашем глазу, который только и воспринимает ощущения ахроматические, вне зависимости от числа колебаний. Поэтому же эта область цветоощущения сохранится надолго, и нельзя себе представить, чтобы здесь в близкое время наступила какая-либо перемена.

Понятия

Идеально-белый цвет мы приписываем той поверхности, которая отражает все падающие на нее лучи света и при этом рассеивает их во все стороны. Хотя еще и не существует исследования, в коем белизна поверхности, обладающей всегда устойчивыми свойствами и по желанию изготовленной, была бы измерена в абсолютной мере, мы и теперь можем признать за бесспорное, что достаточно толстый слой сернокислого барита (сернобариевой соли) ближе всего в этом отношении к идеалу; возможная здесь ошибка может быть выражена лишь немногими сотыми долям, т. е. близка к порожной величине.

Идеально-черный цвет дает такая поверхность, которая не отражает никаких лучей. Ящик с отверстием, хорошо выкрашенный внутри черным, осуществляет этот идеал с точностью, которая лежит далеко за порогом чувствительности (абсолютно черное тело по Кирхгоффу).

Нейтрально-серым цветом обладает такая поверхность, которая отражает одинаковое количество всех падающих на нее лучей. Смеси из черных и белых красителей никогда не бывают нейтрально-серыми, большей частью они имеют синий оттенок вследствие тусклости (Trübungsfarbe). Чтобы сделать их нейтральными, необходимо примешать к ним определенное количество темно-желтого красителя (желтой охры). Удачно ли сделана эта примесь, мы узнаем при помощи вращающегося круга (диска) или другим путем оптического смешения чисто белого и чисто черного цвета и сравнения полученных таким образом смесей с цветом данной составленной нами краски. При этом легко бывает заметить остаток хроматического цвета; сообразно с этим смесь меняют до тех пор, пока не получится полное тождество окраски с нейтрально-серым.

Так как мы привыкли к синеватому оттенку серого цвета, получаемого от смешения соответствующих красителей, то нейтрально-серый цвет вначале кажется нам коричневатым, «мышиным», серым. Но очень скоро в нашей памяти прочно устанавливается представление чисто серого цвета и приобретается уверенность суждения при сравнениях. Однако после рассматривания хроматических цветов эта способность оценки на короткое время расстраивается благодаря возникновению последовательных образов.

Характеристика ахроматического ряда

Ряды ахроматических цветов также постепенны и непрерывны, как и все другие ряды цветов. Между идеально-черным и идеально-белым можно вставить бесконечно большое число средних ступеней, близких друг к другу настолько, что разница между ними будут лежать ниже порога.

Ахроматические цвета образуют одномерный ряд or темного к светлому, с белым и черным на концах. Каждый серый цвет имеет вполне определенное место в этом ряду, так что все вышележащие цвета выглядят темнее, а все ниже лежащие – светлее. Перейти от одного серого цвета к другому можно только по одному пути, а именно – через промежуточные серые цвета.

Благодаря существованию порога различения для ощущений серых цветов число различимых ступеней серого конечно. Для среднего глаза оно колеблется между 300 и 400.

Измерение ахроматических цветов

Ахроматические цвета можно измерять только обладая идеально белой поверхностью или такой поверхностью, у которой известно ее отношение к идеальному белому цвету. Тогда постепенно уменьшают количественно-учитываемым образом освещение этой белой поверхности до тех пор, пока она не станет такой же серой, как та поверхность, которую мы с ней сравниваем. Теперь обе поверхности отражают одинаковое количество света, потому что мы их уравняли. Так как количество света отраженного нашей белой поверхностью нам известно, то мы узнаем и ту долю белого света, которую отражает данная измеряемая серая поверхность, в зависимости от своих особенностей.

Такого рода измерения можно производить любым фотометром. Специально для этой цели сконструированный полутеневой фотометр мною описан в другом: месте – «Physikalische Farbenlehre». 2 aufl. S. 80. Leipzig, 1923.

Всякий серый цвет определяется его светлотой (Helligkeit) или содержанием в нем белого цвета, т. е. тем количеством белого света, которое он отражает. Все эти числовые величины – суть правильные дроби. Каждый серый цвет можно выразить уравнением W + S = 1, где W означает содержание белого, a S – черного. Если W = О, то мы имеем дело с идеально черным; если же S = 0, то перед нами идеально белая поверхность.

Точность этих измерений в лучшем случае доходит до 0,2–0,3 % благодаря существованию порога ощущения. Для практических целей обычно достаточно и одной десятой этой точности, и даже меньше. В особенности там, где оценка производится с точки зрения эстетической, пределы ошибок могут доходить до 10 % наличного содержания белого.

Для краткости, количественные индексы серых цветов изображают не просто дробью (десятичной), а лишь двумя цифрами, отбрасывая запятую и ноль, стоящий перед ними. Таким образом серый 25 содержит 0,25 белого, а черный с содержанием 0,04 белого выражается в виде 04.

Закон Фехнера

Если мы построим ряд ахроматических цветов, которые содержат 1,0, 0,9, 0,8, 0,7, 0,6 до 0,1 и 0,0 белого, то он никоим образом не будет производить впечатления ряда одинаковоудаленных друг от друга ступеней. Между 1,0, 0,9, 0,8 и т. д. различия так незначительны, что на первый взгляд их вовсе нельзя отличить друг от друга; зато между 0,2, 0,1 и 0,0 образуются слишком большие переходы. Для получения одинаковых расстояний мы должны ступени в белом конце увеличить, а в черном уменьшить.

Это следует из закона Фехнера. Как раздражение в этом случае мы должны рассматривать количество белого цвета, которое содержится в данных ахроматических цветах. По закону же Фехнера эти количества только тогда могут вызвать равномерно отстоящие друг от друга ступени серого цвета, когда сами они расположены в геометрический ряд.

Возникает лишь вопрос: какой же знаменатель надо брать? Принимая во внимание требования рационального нормирования – о чем речь впереди – мы должны поступить следующим образом. Так как все наши исчисления ведутся по десятичной системе, то мы вначале выражаем ступени серого ряда с содержанием белого в количествах: 1,00, 0,10, 0,01, 0,001 и т. д. Таким образом, мы получаем нисходящий геометрический ряд с фактором 1/10. Но, очевидно, что эти ступени будут слишком большими.

Необходимо каждую из них разделить, следуя десятичной системе, еще на 10 ступеней. Эти ступени можно найти, если взять числа, соответствующие логарифмам, равным 1,000, 0,900, 0,800, 0,700, 0,600…0,100 и принять наибольшее из них за 1. Таковыми окажутся в результате числа 1,00, 0,79, 0,63, 0,50, 0,40, 0,32, 0,25, 0,16, 0,125, 0,100. Если вставим десять ступеней между 0,100 и 0,010, то найдем эти же числа, только в десять раз уменьшенные. То же повторится между 0,010 и 0,001 и т. д. Так как разница между двумя ступенями в среднем составляет около 20 %, то она лежит значительно выше порога, а потому ощутима. Дальнейшее деление на десять новых, более мелких ступеней, неприемлемо, так как разница между этими делениями будет лежать уже ниже порога различения.

Данные величины делят непрерывный серый ряд на одинаково отстоящие для нашего восприятия отрезки. Нам же нужны не отрезки, а точки – т. е. определенные серые цвета. Эти цвета мы и можем получать посредством смешения всех цветов каждого данного отрезка ряда. Соответствующие им числа суть средние геометрические двух граничных чисел. Мы получаем, таким образом, следующий ряд, который обозначаем сокращенно, как было указано выше, цифрами, показывающими процентное содержание белого цвета:

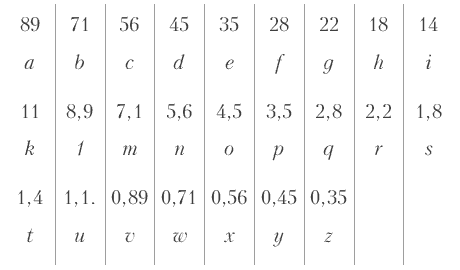
Мы заканчиваем наш ряд на 0,35, так как очень мало таких поверхностей, которые бы отражали света так мало или еще меньше. Теоретически можно продолжать этот ряд до бесконечности. Под числами находятся буквы латинской азбуки, которые обозначают ступени серого ряда, так же, как в музыке тона обозначаются буквами. Каждая буква может обозначать написанное над нею количество белого света (в процентах) или количество черного цвета, если возьмем число дополнительное до 100. Таким образом, буква i может означать 14 % белого цвета или 86 % черного. На практике для большинства случаев эти деления еще слишком мелки. Поэтому мы из каждых двух чисел опускаем одно и получаем практический серый ряд (шкалу бело-черного). Мы обрываем его на букве р, так как у буквы р находится самый глубокий черный цвет, который можно получить на бумаге при помощи типографской черной туши:

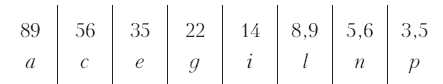
На прилагаемой таблице № 1 эти ступени а с е g i l n p и представлены. Очень хорошо было бы заучить их наизусть, для того чтобы можно было различать ступени серых цветов: и не имея перед глазами масштаба для сравнения. Для неопытного человека, который ничего не знает о расположении цветов, мысль о таком заучивании покажется абсурдом. Но нужно только попробовать это сделать, чтобы убедиться в ее осуществимости. Такое заучивание совершенно осваивает нас с миром ахроматических цветов.

Бесконечность и порог ощущения

Приведенный выше геометрический ряд серых цветов начинается с идеально-белого цвета, который вполне определяется условиями полного отражения и рассеивания. Хотя И. Ламберт еще в XVII веке дал такое определение белому цвету и это определение нашло свое применение и в других отраслях науки, как, например, в астрономии, – для авторов, работающих в области науки о цветах, оно осталось но сей день чуждым. Даже Геринг приводит хорошо известный опыт (с отражением дневного света от посеребренного покровного стеклышка, лежащего на белой бумаге) – имеющий целью доказать, что белый цвет можно усиливать безгранично. Мы тут наталкиваемся на ошибочное смешение белого цвета с блеском. Посеребренное покровное стеклышко не рассеивает свет, а только отражает его; оно поэтому не белое, а блестящее.

Несколько иначе проявляет себя черный конец ряда. Первый, описанный нами выше, ахроматический ряд был расположен непосредственно по степеням светлоты и носит поэтому название аналитического ряда и заканчивается черным цветом со светлотой, равняющейся нулю. Такой черный цвет мы можем всегда воспроизвести в отверстии ящика, окрашенного изнутри в черный цвет. Не существует, однако, ни одного такого красящего вещества, которое дало бы этот черный цвет, в чем мы легко убеждаемся, когда сравниваем различные черные окраски с таким отверстием вычерненного внутри ящика. Составленный согласно закону Фехнера геометрический ряд выражает этот факт тем, что совершенно черный цвет является в нем бесконечно удаленным. Сколько бы мы ни продолжали этот ряд, всегда можно прибавить еще одну ступень, которая была бы меньше предыдущей в определенном количественном отношении.

На практике все-таки этот ряд имеет предел благодаря вышеозначенному свойству всех черных тел отражать всегда и некоторое измеримое количество белых лучей. Этот предел очень непостоянен и с развитием техники постепенно удаляется.

Здесь необходимо вспомнить также и о существовании порога ощущения, благодаря которому при известной силе света наше ощущение этого света уже прекращается, так как раздражение лежит ниже порога, а поэтому для нас неощутимо. Этим обстоятельством вызывается необходимость дать цветовому ряду законченный вид.

Тут же необходимо указать и на следующее: шкала серых цветов, изображенная в виде нисходящего геометрического ряда, представляет собой не один только «ряд Фехнера», а бесконечное множество таковых. Это происходит оттого, что таковой ряд выражает ведь не силу падающего света, но величины отражения. В зависимости от силы освещения, ступени шкалы будут давать самые различные количества света. В особенности при слабом свете – многие ступени конца черного ряда могут опуститься ниже порога и будут все выглядеть черными.

В этом можно убедиться, рассматривая такую шкалу в сумерках. При хорошем же свете даже ступени r и t находятся выше порога чувствительности и их можно легко отличить друг от друга.

Это и послужило причиной того, что при выработке шкалы мы пользовались исключительно законом Фехнера, не обращая внимания на порог чувствительности в темном конце. Включение этого обстоятельства оправдало бы себя только при определенном освещении, не говоря уже о существовании индивидуальных различий в величине порога. Шкала, предназначенная для общего пользования, не должна содержать этих переменных величин, если мы желаем, чтоб она была достаточно универсальна. Тот, кто пользуется шкалой, должен со своей стороны обратить внимание на то, какова средняя интенсивность освещения вокруг его рабочего стола. Сообразуясь с этим он и выбирает область шкалы, наиболее ему подходящую.

Пространственная схема

Несмотря на то, что вышеизложенные отношения между аналитической и психологической серой шкалой так просты, что для их объяснения не требуется рисунка, мы все-таки считаем полезным дать таковой. Это необходимо, потому, что в дальнейшем, в более сложном случае, с цветными треугольниками одинаковых тонов, нам придется делать подобные же передвижки, и если мы здесь познакомимся с более простым случаем, то в дальнейшем нам будет легче понять все излагаемое.

На рис. 4 левое деление представляет собою аналитическую гамму, разделенную на сто ступеней. Правое деление представляет собой точки acegilnprt практической шкалы серых цветов, расположенных соответственно содержанию в них белого цвета. Из рисунка видно, как велики расстояния ас и cl, как они быстро уменьшаются и в точках r и t так приближаются друг к другу, что становится невозможным нанести между ними еще какие-нибудь точки. Теоретически все-таки мы должны поместить между точкой t и конечной точкой еще бесконечное множество ступеней шкалы серого.

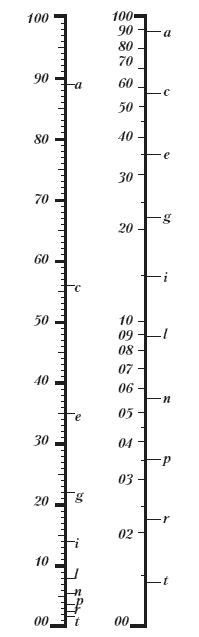
Рис. 4

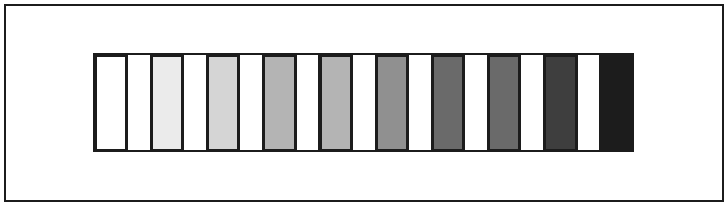
Рис. 5

Мы можем представить это изображение и в другом виде, расположив ступени серой шкалы, которые мы воспринимаем, как равно отстоящие друг от друга, на одинаковых расстояниях друг от друга, как то сделано на рисунке шкалы (рис. 5). В таком случае масштаб, обозначающий количество белого, мы должны уже нарушить так, что точки вблизи белого будут сближены друг с другом, точки же, лежащие к темному концу, – все больше раздвинуты. Левая сторона правого рисунка рис. 4 и изображает такие деления, которые соответствуют одинаковоотстоящим друг от друга, ступеням Фехнеровского ряда, написанным справа. Деления слева соответствуют логарифмической счетной линейке. В направлении сверху вниз они соответствуют нисходящему геометрическому ряду и повторяются между 10 и 01, так же как между 100 и 10, с той только разницей, что величины расстояния между ними здесь в десять раз меньше. Теоретически мы это деление можем продолжать до бесконечности, с интервалами от 01 до 001, от 001 до 0001 и так далее. Практически к этому прибегать не приходится, так как существует очень мало поверхностей, которые отражают меньше одной сотой доли падающего на них света. Здесь мы имеем, следовательно, изображенными графически, те самые отношения, о которых только что говорили выше. Такое деление, как на рис. 5, называется логарифмическим делением. Шкалу серых цветов, расположенную согласно закону Фехнера, тоже поэтому называют логарифмическим рядом или логарифмической шкалой. Такое логарифмическое деление всегда необходимо там, где закон Фехнера находит свое применение. Это касается особенно всякого рода нормировки, значение коей для работы и обихода необычайно велико. И самым ценным следствием внесения в науку о цветах меры и числа является именно возможность ныне нормировать весь мир цветов.