Физика повседневности. От мыльных пузырей до квантовых технологий

3. Интенсивность звука, издаваемого говорящим, уменьшается как 1/R2 по мере удаления от него, при отсутствии препятствий или фокусировки звука в одном направлении

Отсюда следует, что условия полного отражения для звуковой волны, распространяющейся из воды в воздух, не соблюдаются. Когда исходящая от дна моря звуковая волна доходит до поверхности, всегда возникают преломленная и отраженная волны. Еще одно следствие: в случае акустической волны преломленный луч не отклоняется от вертикали, а, наоборот, приближается к ней.

Значит, предположение, что поверхность океана может быть отражающей поверхностью, неверно? Не так быстро! Фактически доля энергии, которая преломляется на границе между водой и воздухом, во многом зависит от угла падения и соотношения скоростей между средами. В случае очень разных скоростей, как в нашей ситуации, интенсивность преломленной (вышедшей в воздух) волны невелика вне зависимости от угла падения. Таким образом, на поверхности океана отражение почти полное: доказано, что не более 1 % интенсивности падающей звуковой волны, распространяющейся почти горизонтально, проходит из воды в воздух. Следовательно, поверхность океана, похоже, способна хорошо отражать звук из глубин…

4. Пример направленного распространения акустических волн в воздухе. Дети делятся секретом… Держа руку у рта, девочка предотвращает распространение звукового сигнала во всех направлениях

Так что же, мы, наконец, нашли объяснение распространения звука на большие расстояния в океанах? Увы, нет – по двум причинам. Во-первых, часть энергии все равно теряется каждый раз, когда звуковой луч попадает на поверхность океана. Во-вторых, она почти всегда неровная, что препятствует отражению звуковой волны. В конечном счете поверхность океана, за исключением случаев штиля, не может сформировать верхнюю границу природного океанического волновода, который мы пытаемся разыскать. Что касается дна океана, то оно еще меньше подходит для образования такой границы. Донные отложения не отражают звук, а, наоборот, склонны поглощать его. Таким образом, стенки океанического проводника звука должны находиться где-то между дном и поверхностью… именно здесь мы их и обнаружим! Чтобы продолжить наше расследование, давайте подробнее рассмотрим процесс распространения звука в океане.

Скорость звука в морской воде

В такой жидкости, как морская вода, скорость звука зависит от ее свойств, которые неодинаковы в разных частях океана. Здесь и находится ключ к решению нашей задачи! В зависимости от содержания соли, температуры и давления воды, скорость звука варьирует от 1400 до 1540 м/с. Например, давление на глубине возрастает, что, как правило, делает звук быстрее. Также звук распространяется быстрее при более высокой температуре. Но более плотная холодная вода опускается на дно океана. Эти два противодействующих эффекта объясняют изменение скорости звука в зависимости от глубины (илл. 5). В непосредственной близости от поверхности резкое понижение температуры сначала приводит к постепенному уменьшению скорости звука c. На больших глубинах изменение температуры не так ощутимо, преобладает эффект увеличения давления, и это приводит к возрастанию c по мере приближения ко дну. Глубина zm чаще всего составляет от 1000 до 1200 м, но может достигать и 2000 м на низких широтах, где теплым остается более толстый слой воды. В высоких широтах, наоборот, zm может составлять всего 500 или даже 200 м, или еще меньше в полярных регионах. Изменение солености в зависимости от глубины, как правило, незначительно и не оказывает заметного эффекта.

Отражение и преломление световых волн

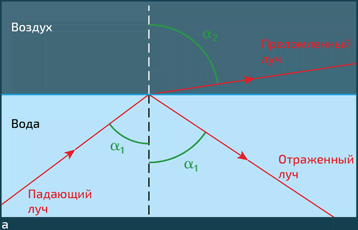
Напомним свойства отражения и преломления в случае оптики. Если луч света из среды 1 попадает на границу (предположительно плоскую) со средой 2, часть света отражается в среду 1, а другая часть проходит в среду 2 (см. илл. а): это явление преломления. Угол преломления α2 связан с углом падения α1 законом Снеллиуса:

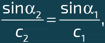
где c1 и c2 – скорости света соответственно в средах 1 и 2.

Эту формулу можно также написать, используя индексы преломления сред 1 и 2, соответственно n1 = c/c1 и n2 = c/c2, где c – скорость света в вакууме.

Если световой луч попадает на поверхность с достаточно большим углом падения α1, то величина

становится больше 1, и не существует такого значения угла α2, которое соответствовало бы приведенной выше формуле. Таким образом, преломление луча оказывается невозможным, и происходит полное внутреннее отражение (см. илл. b). Это явление используется в оптических волноводах: луч претерпевает целый ряд отражений внутри проводника, и поэтому свет распространяется по нему с минимальными потерями. Самый известный пример оптического волновода – оптоволокно.

Как и световые волны, звуковые волны могут отражаться и преломляться. Формула Снеллиуса остается применимой и к описанию поведения «звуковых лучей», но c 1 и c 2 в этом случае, очевидно, представляют собой скорости звука, а не света.

Преломление и отражение светового луча (красные стрелки), выходящего из воды (показатель преломления равен 1,33) в воздух (показатель преломления близок к 1,0)

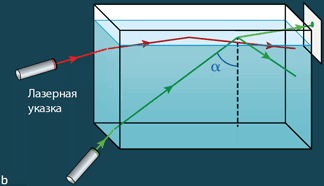
Опыт с лазерными указками демонстрирует явление полного отражения на границе между водой и воздухом. Луч, падающий на поверхность воды под небольшим углом α (зеленый), подвергается лишь частичному отражению: часть энергии покидает воду с преломленным лучом, и на экране появляется световое пятно. Скользящий луч (красный) испытывает полное внутреннее отражение

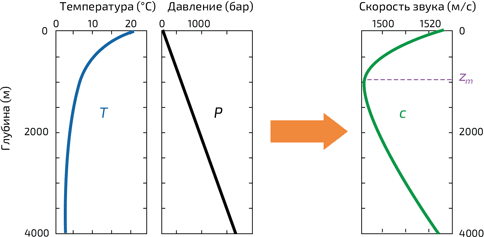
5. Пример изменения скорости звука с в океане в зависимости от глубины. В результате повышения давления и понижения температуры по мере приближения ко дну скорость достигает минимума на глубине zm, чаще всего около 1000 м

Когда звук распространяется зигзагами

Теперь рассмотрим звуковой луч, источник которого находится на глубине zm. Независимо от того, пойдет ли он вверх или вниз, в области, в которой он оказывается, скорость звука выше, чем на оси. Таким образом, в результате последовательного прохождения слоев воды на своем пути звуковой луч постепенно искривляется, вплоть до скользящего падения под таким углом, для которого происходит полное отражение (см. врезку). Тогда он начинает искривляться в направлении увеличения (или уменьшения) глубины, пока снова не достигнет глубины zm, где изменение скорости звука меняет знак. Таким образом, луч движется по зигзагообразной траектории между двумя плоскостями (илл. 6).

Эти две плоскости эквивалентны верхней и нижней границам волновода, у которого нет боковых стенок. Тем не менее благодаря описанному явлению звук способен распространяться в океане на большие расстояния. Наконец-то мы закончили расследование!

Эффективность океанического волновода

Не все исходящие из источника звуковые лучи попадают в этот «океанический волновод». Первоначально звук из источника распространяется во всех направлениях, и превращение его в «звуковой луч» зависит от угла, образующегося между ним и вертикалью. Если этот угол достаточно велик, то звуковой луч распространяется безгранично. Если же угол слишком мал, звуковой луч достигнет поверхности или дна океана. Но дно океана неровное, и оно, как и поверхность (кроме редких моментов, когда она совершенно спокойна), рассеивает звук. Таким образом, море, как правило, может послужить волноводом только для звуковых лучей, которые не достигают ни поверхности, ни дна океана. На практике существуют «акустические каналы», по которым звук передается на большие расстояния, и «теневые зоны», куда звук никогда не попадает.

Звуковые волноводы, созданные человеком

Распространение звука в газах или жидкостях представляет собой возмущение, периодически изменяющее в пространстве и времени плотность частиц, эту среду составляющих. Любой выделенный объем жидкости локально подвергается периодической череде сжатий и расширений.

Скорость звука в жидкостях и твердых телах, вообще говоря, выше, чем в газах. Это и не удивительно, ведь в вакууме звук не распространяется вообще, а разреженный газ имеет плотность промежуточную между вакуумом и конденсированным веществом. Однако если скорость звука в двух средах сильно отличается, то передача звука из одной в другую может быть затруднена. Это явление используется в стетоскопе – инструменте, который доносит в ухо врача звуки из грудной клетки пациента. Первоначально он представлял собой простую деревянную трубку.

Другой пример волновода, основанного на явлении полного отражения, которое возникает при переходе звука из воздуха в твердое тело, – это старинная система акустических труб, соединяющая различные уровни на кораблях. Сделанная обычно из меди или латуни, она передает приказ с капитанского мостика в машинное отделение. В таком волноводе волна практически одномерна – это означает, что интенсивность звуковой волны остается постоянной по всей длине трубы, даже на удалении от источника. Затухание звука в воздухе настолько низкое, что, если бы можно было построить прямую трубку длиной 750 км и избежать поглощения звука стенками, она послужила бы телефоном между Парижем и Марселем. К сожалению, скорость звука в воздухе составляет всего 340 м/с, так что слова из Парижа в Марсель добирались бы более получаса…

Изучение распространения звука в океанах серьезно интересовало британских и американских ученых во время Второй мировой войны. Тогда речь шла об обнаружении немецких подводных лодок раньше, чем они подплывут достаточно близко, чтобы атаковать американские или английские суда. Акустическое обнаружение подводных лодок с помощью сонаров сыграло важную роль в битве за Атлантику: в 1943 году, после тяжелых потерь, союзники сумели уничтожить значительное количество немецких подлодок, установив тем самым свое превосходство на море.

6. Акустический луч (красный), излучаемый на глубине zm, проходит между двумя плоскостями, от которых он полностью отражается. Зависимость скорости звука от глубины c (z) в океане представлена зеленой кривой. Значения z1 и z2 (считаем, что глубина равна 0 на поверхности) зависят от угла падения луча на глубине zm и определяются законом Снеллиуса: c (z1) = c (z2) = cm/sin α (zm)

Простая модель

Интересно рассмотреть случай, когда скорость звука c – простая функция глубины z. Например, функция, имеющая минимум в zm: c (z) = c (zm) + k (z – zm) 2, где k – константа. В этом случае кривая, иллюстрирующая изменение скорости звука в зависимости от глубины (зеленая на илл. 5 и 6), является параболой. На самом деле это приближение почти всегда справедливо для глубин z, близких к zm. Звуковой луч, немного отклоняющийся от горизонтали, следует по синусоиде, период которой не зависит от угла падения, так что все звуковые лучи в одной вертикальной плоскости сходятся в точках оси z = zm (илл. 7). Эти точки аналогичны фокусам оптических приборов, таких как линзы, в которых сходятся падающие световые лучи, поэтому наблюдается явление фокусировки звуковых волн. Параболическая форма кривой хорошо описывает изменение скорости звука в зависимости от частоты в глубинах океана. Однако, поскольку кривая c (z) на практике не является параболой, то фокусировка звука не идеальна.

Заключение

Когда звук излучается на соответствующей глубине в море, значительная часть звуковой энергии оказывается заперта в «акустических каналах». Достаточное ли это объяснение для прохождения звука от Австралии до Бермудских островов? Попробуем подсчитать. Хотя рассмотренный нами механизм описывает именно распространение звука в океане, остаются возможными еще два направления. Звуковая волна, излучаемая в середине океана, проходит в течение времени t расстояние R порядка сзв. t, где сзв. – средняя скорость звука в воде, скажем, 1500 м/с. Даже если предполагается, что потери равны нулю, энергия звуковой волны должна распределяться по всей, примерно цилиндрической, поверхности зоны 2πRh, где разница в глубине h между верхней и нижней границами канала может достигать глубины океана. Таким образом, интенсивность звука уменьшается как 1/R по мере удаления от источника. Это происходит не так резко, как затухание, пропорциональное 1/R2 звука в воздухе (илл. 3), но и оно едва ли оставляет надежду на то, что звук, раздавшийся в Австралии, будет услышан на Бермудах. Однако если приемник звука находился в точке фокуса, где сходятся звуковые лучи (илл. 7), а величина h невелика, то в принципе отголосок взрыва мог быть услышан. Кроме того, можно допустить, что колебания солености и температуры в толще океана на пути звуковых лучей создают и вертикальные отражающие стенки, препятствующие рассеянию энергии звуковой волны. И все же удивительно, что звук достигает Бермудских островов в обход мыса Доброй Надежды, учитывая дополнительное поглощение энергии, например, пузырьками воздуха или планктоном.

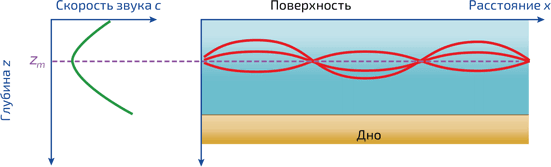
7. Явление фокусировки звуковых лучей

8. Пример миража в Ливийской пустыне. По мере приближения к раскаленному песку солнечные лучи встречают все более горячий воздух (и, следовательно, среду с уменьшающимся показателем преломления): таким образом, они, как и звуковые лучи на илл. 7, все сильнее отклоняются вплоть до отражения. Наблюдателю кажется, что в продолжении этих отраженных лучей он видит воду

Распространение звука в естественных подводных каналах – не единственный случай волновода, созданного природой. Еще несколько примеров связаны со спецификой распространения электромагнитных волн. Наиболее эффектны миражи, которые возникают из-за непрямолинейного распространения света в очень неравномерно нагретой атмосфере (илл. 8). Кроме того, можно вспомнить короткие радиоволны, которые распространяются на большие расстояния благодаря отражению в ионосфере – верхней области атмосферы на высоте от 60 до 800 км. При определенных условиях радиоприемник может принимать радиопередачи из других стран.

Глава 3

Цвета моря и неба

Когда стоит хорошая погода, днем небо голубое, а в сумерках – алое. Через несколько часов опускается ночная тьма, и на черном небе вспыхивают мириады звезд. Днем облака белые или сероватые. В дождливую погоду иногда появляется радуга… Какие физические принципы объясняют все эти цвета? Ответ вы найдете в этой главе. И поскольку речь идет о небесах, мы поговорим и об их крылатых обитателях– птицах и насекомых.

Море и небо дарят нам разнообразные цвета, вдохновившие многих художников. Аркадий Рылов воспроизвел эти цвета на картине, выставленной в Третьяковской галерее в Москве (илл. 1). Белые хмурые облака плывут по небу всех оттенков синего. Поверхность моря более темная, подошвы волн – почти черные, а гребни местами образуют белые «барашки».

Цвет моря и сила ветра

Количество «барашков» и высота волн зависят от скорости ветра. Эта информация имеет важное значение для моряков: для определения скорости ветра они пользуются эмпирической таблицей, которую разработал британский адмирал сэр Фрэнсис Бофорт (1774–1857) (см. главу 2). На картине Рылова наличие небольшого количества «барашков» свидетельствует о ветре 12–19 км/ч, то есть 7–10 морских узлов. Такой ветер считается слабым и соответствует силе в 3 балла по шкале Бофорта.

1. «В голубом просторе», картина художника-символиста Аркадия Рылова (1870–1939)

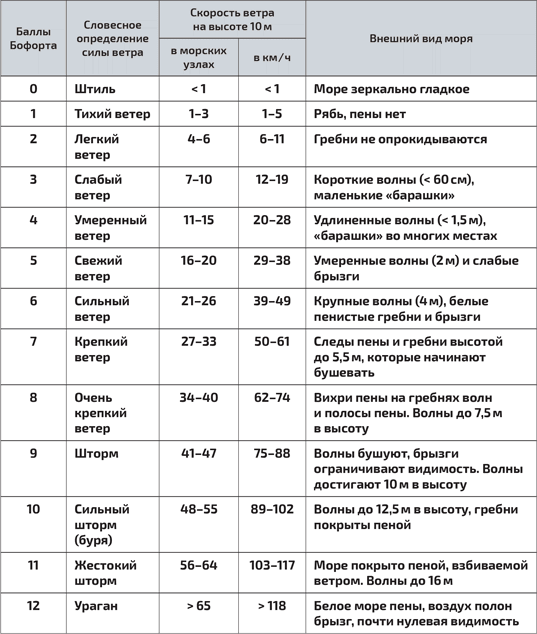
Шкала Бофорта

Представление о скорости ветра можно получить не только с помощью шкалы Бофорта, но и по контрасту между яркостью моря и неба. Они одинаковы, когда на море штиль, а горизонт едва различим. Как правило, легчайшего ветра достаточно, чтобы встревожить поверхность воды и создать контраст: небо ярче моря, горизонт выглядит как четкая линия. Это явление было изучено несколько десятилетий назад российскими учеными на борту исследовательского судна «Дмитрий Менделеев»

Яркость морской поверхности зависит от угла наблюдения. Действительно, луч света, падающий на поверхность моря, как частично преломляется, так и частично отражается (см. главу 2, «Отражение и преломление световых волн»). Интенсивность отраженного луча зависит, в частности, от показателя преломления воды и угла падения. Чем острее угол, тем сильнее отражение. Поэтому поверхность моря кажется более яркой у горизонта, чем вблизи наблюдателя.

А что насчет его цвета? Цвет поверхности практически непредсказуем, так как зависит от многих факторов, таких как глубина моря, положение солнца, цвет неба, наличие взвешенных частиц и водорослей и т. д. Все эти факторы влияют на отражение света от поверхности, его рассеяние и поглощение в воде. И все же море чаще всего синее. Причина в том, что вода поглощает меньше света в диапазоне между 400 и 500 нм (синего), чем в остальной части видимого спектра (см. ниже). Да, вода поглощает мало синего! Стакан воды выглядит совершенно прозрачным. Но начиная с толщины в несколько метров вода начинает заметно поглощать свет.

Цветовое зрение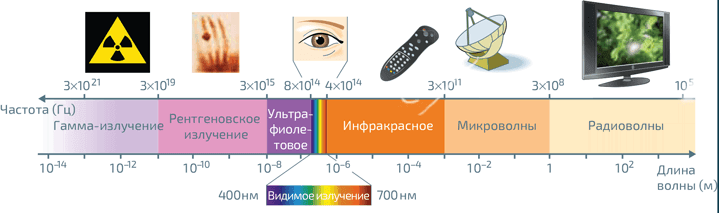

Различные области электромагнитного излучения и их применение. Узкая область между 400 и 800 нм (то есть на частотах между 800 и 400 ТГц) соответствует видимому спектру. Каждое излучение, или «спектральный цвет», обладает своей длиной волны λ, которая связана с частотой υ отношением λ = c/υ, где c – скорость света в вакууме

Человеческий глаз чувствителен к электромагнитному излучению волн длиной от 400 до 800 нм (см. илл.). Объекты кажутся цветными, либо когда они излучают свет, будучи достаточно нагретыми (как кусок раскаленного железа), либо когда они освещены и «рассеивают» (иными словами, возвращают) часть полученного света извне. Свет, попадающий в глаза, обычно полихроматичен, то есть содержит излучения с различными длинами волны в разных пропорциях. Эта композиция и определяет воспринимаемый нами цвет. Таким образом, объект, поглощающий все световое излучение, кажется черным; объект, излучающий электромагнитное излучение всех длин волн от 400 до 800 нм с сопоставимой интенсивностью, выглядит белым.

В глазу цветовое восприятие обеспечивается клетками, называемыми колбочками, которые выстилают заднюю поверхность сетчатки. Существует три типа колбочек (см. илл.), передающих сигналы в мозг, который интерпретирует их и получает визуальное ощущение цвета. Воспринимаемые цвета не ограничиваются цветами радуги или «спектральными цветами», которые возникают вследствие разложения белого света. Пурпурный, например, получается путем объединения красного (около 680 нм) и синего (около 480 нм) света. Кроме того, один и тот же воспринимаемый цвет может соответствовать свету самых разных композиций. Например, объект может казаться желтым, когда он излучает монохроматический свет длиной волны около 580 нм, или излучает свет видимого диапазона, лишенный своей сине-фиолетовой части, или даже комбинацию красного и зеленого светов.

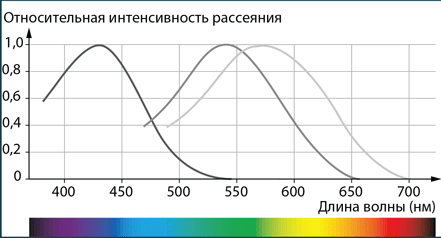
Чувствительность трех типов колбочек в зависимости от длины волны

Цвет неба в хорошую погоду

В то время как предсказать цвет моря непросто, цвет неба в хорошую погоду легко объясняется физическими принципами, выявленными английским физиком лордом Рэйли (Рэлеем) (1842–1919). В отсутствие облаков цвет неба определяется результатом взаимодействия солнечного излучения с компонентами атмосферы Земли, а именно с неоднородностями (флуктуациями) плотности молекул азота и кислорода.

Как эти молекулы ведут себя, попав в поле солнечного излучения? Рассмотрим монохроматический свет, обладающий заданной длиной волны λ. Он представляет собой колеблющиеся в плоскостях, перпендикулярных направлению распространения света, с частотой υ магнитное и электрическое поля. Под действием колеблющегося электрического поля электроны в молекулах также колеблются с частотой υ. В результате и сама молекула становится маленьким излучателем, испуская свет той же частоты, что и падающая волна. Это похоже на то, как излучает электромагнитные радиоволны теле- или радиоантенна. В случае молекул и солнечного света длина его волны оказывается много большей размера молекул, и такое рассеяние называется «рассеянием Рэлея». Расчеты показывают, что интенсивность рассеянного света оказывается пропорциональной четвертой степени частоты υ4 (или 1/λ4). Это утверждение называется законом Рэлея – Джинса (илл. 2).

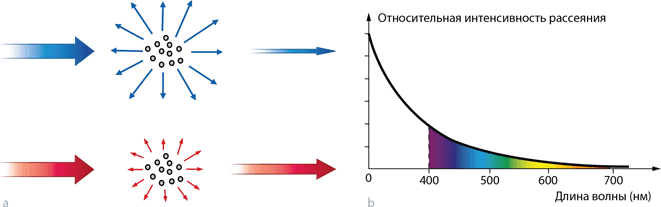
2. Рассеяние света молекулами и закон Рэлея. Под воздействием падающего монохроматического света (a) молекулы переизлучают свет той же длины волны во всех направлениях. Синему цвету соответствует длина волны около 450 нм, а красному – около 650 нм. (b) Согласно закону Рэлея, четвертая степень отношения 650/450 равна 4,3, то есть интенсивность рассеяния синего примерно в 4 раза выше, чем красного

Как все это связано с цветом неба? Согласно закону Рэлея, рассеяние электромагнитных волн оказывается значительно интенсивнее для высоких частот по сравнению с низкими. Это означает, что молекулы атмосферы сильнее рассеивают синий цвет, чем красный, зеленый или желтый. Таким образом, наших глаз преимущественно достигают именно световые лучи синего цвета. Вот почему небо синее! Следуя этому рассуждению, можно было бы предположить, что небо должно быть фиолетовым, так как фиолетовое излучение обладает более высокой частотой, чем синее. В действительности в спектре солнечного излучения доля фиолетового меньше, чем синего. Кроме того, и максимальная чувствительность человеческого глаза находится в области зеленого (555 нм). В результате фиолетовая часть спектра солнечного излучения оказывается подавленной в восприятии человеческого глаза, и небо видится синим (см. главу 3, «Цветовое зрение»).

3. a. Днем чистое небо кажется синим, так как молекулы атмосферы сильно рассеивают синюю компоненту солнечного излучения.

b. На закате доходящий до нас солнечный свет преодолевает гораздо более толстый слой атмосферы, и небо пламенеет

Небо на закате… и после

На закате небо над горизонтом принимает красивый розовый оттенок (илл. 3). Этот цвет также обусловлен рассеянием солнечного света в атмосфере. Поскольку свет распространяется во всех направлениях, то до нас доходит лишь его часть, а остальное возвращается в пространство. Часть солнечной энергии, возвращающаяся за пределы земной атмосферы, невелика, однако для некоторых явлений она может оказаться существенной (илл. 4). В видимом излучении разница между энергией, получаемой поверхностью земли и верхними слоями атмосферы, обусловлена прежде всего рассеянием. Так, мы видим, что в дневное время энергия, получаемая на земле, меньше падающей на верхние слои атмосферы примерно на 25 % в синем и на 10 % – в красном диапазонах. На закате эти пропорции изменяются, поскольку свету приходится преодолевать гораздо большую толщу атмосферы (илл. 5). Таким образом, синий свет почти целиком рассеивается, и наблюдатель на земле видит в основном красный.