Слова и числа

Третий по распространенности арабский алфавит. Он происходит от арамейского и возник примерно в 4 веке нашей эры. Арабский алфавит содержит 28 букв для обозначения согласных, а гласные пишутся выше или ниже согласных. Порядок записи знаков справа налево. Необычным в нем является и то, что одна и та же буква пишется неодинаково в зависимости от того, какое место она занимает – стоит отдельно, или стоит в начале слова, в середине, в конце. Можно много говорить о разнообразии и своеобразии чужих алфавитов, но пора заострить внимание на родном – русском.

Создателями славянской азбуки были просвещённые братья Кирилл и Мефодий, происходившие родом из греческого города Салоники. Приблизительно в середине 9 века они перевели с греческого на старославянский язык христианские богослужебные книги. Отдавая им дань уважения, следует заметить, что в происхождении двух славянских алфавитов глаголицы и кириллицы остается много неразгаданного. Большинство ученых считают, что Кирилл создал все-таки глаголицу, а кириллица была составлена в Восточной Болгарии для приближения славянского письма к торжественному византийскому. До 11-12 веков кириллица и глаголица употреблялись параллельно, впоследствии кириллица вытеснила глаголицу. Состав и форма букв кириллицы изменялись с течением времени. Серьезную реформу русской азбуки провел Петр I в 1708 и 1710 годах. Он изъял несколько дублетных букв, обозначающих один и тот же звук, ввел в состав алфавита букву э, установил разное начертание прописных и строчных букв, отменил цифровое значение кириллических букв и ввел арабские цифры, утвердил графику гражданского шрифта для печати светских книг.

Реформы Петра I затрагивали состав алфавита и графику, но не коснулись орфографии, то есть правописания, которое оставалось очень сложным. Провести дальнейшее упорядочение алфавита и упрощение правописания, следовательно, его демократизацию, удалось только в 1917-1918 годах. Чтобы ни говорили о советской власти современные реформаторы, но писать стало проще и удалось добиться всеобщей грамотности населения огромной страны. Только некоторых почитателей старины даже в наше время так и тянет написать коммерсантъ.

Устная речь состоит из звуков. В письменной речи звуки обозначаются буквами. Сейчас вы читаете текст, и далее повествование будет проходить в письменном виде, поэтому теперь наш путь обратно от буквы к слову.

Буквы – это условные знаки, которыми обозначаются звуки речи на письме.

В русском языке 33 буквы. Перечень букв, в принятом порядке называется алфавитом.

Буквы делятся на гласные и согласные. В русском алфавите 10 гласных букв: а, е, ё, и, о, у, ы, э, ю, я;

20 согласных букв: б, в, г, д, ж, з, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ, и остаются ещё три сиротинушки.

й – одиннадцатая буква русского алфавита, называется и краткое, обозначает полугласный звук. Звук й не образует слога и тем сходен с согласным.

Буквы ъ и ь не обозначают никаких звуков.

ъ – двадцать восьмая буква русского алфавита, называется твердый знак. В современной орфографии употребляется лишь как разделительный знак (например: разъезд, объявление).

ь – тридцатая буква русского алфавита, называется мягкий знак. Её употребление в современной орфографии гораздо шире:

– для обозначения мягкости предшествующего согласного;

– как разделительный знак перед я, ю, е, ё;

– в окончании именительного и винительного падежей единственного числа существительных женского рода на ч и щ, а также на ж и ш;

– в повелительной форме глагола, оканчивающегося на ч, ш, ж;

– в неопределенной форме глагола;

– во 2-ом лице единственного числа настоящего и будущего простого времени.

Согласные в свою очередь делятся на 10 звонких и 10 глухих. Кроме того, 4 согласные буквы называются шипящими, причем одна из них (ж) находится в звонких, а три (ч, ш, щ) в глухих согласных. Это неизменные атрибуты букв. Но есть еще деление букв, которое не является постоянным, а изменяется в зависимости от слов, в которых они употребляются.

Гласные буквы делятся на ударные и безударные. Если в слове больше одного слога, то слоги произносятся с разной силой. Один из них выделяется голосом, он называется ударным. Гласная буква в слове, на которую приходится ударение, называется ударной; все остальные гласные в слове называются безударными.

Большинство согласных в слове бывают твердыми или мягкими. На письме мягкость предшествующего согласного обозначается буквами е, ё, и, ь, ю, я. Причем согласные ж, ц, ш в русском языке произносятся всегда твердо, а согласные ч, щ – только мягко.

Все буквы могут быть написаны большими (прописными) или маленькими (строчными). Большая буква начинает предложение, с большой буквы пишутся имена собственные, различные названия.

Система письма, основанная на подобном алфавите, называется консонантно-вокалической, то есть согласно-гласной.

Со стороны наш алфавит кажется четкой устоявшейся системой, и только присмотревшись, понимаешь, не все пока бесспорно. В среде филологов нет единого мнения по поводу буквы ё: одни её считают полноправным членом алфавита, другие – нет. Что греха таить, при наборе текста на клавиатуре мы редко употребляем эту букву, заменяя её буквой е. Даже клавиша с этой буквой спряталась в левом верхнем углу клавиатуры, и нажимаем мы её реже других, только когда особо держим в голове, что нужно набрать именно эту букву. В результате приходится сталкиваться с поразительными фактами. В солидном словаре:

Словарь русского языка: В 4-х т.

АН СССР, Ин-т рус. яз.;

под. ред. А П. Евгеньевой

М.: Русский язык, 1985-1988,

приведен полный алфавит в начале каждого тома. В самом же словаре про букву е сказано, что она шестая, про букву и сказано, что она девятая, буква у – двадцатая, э – тридцать первая, я – тридцать третья. Посмотрите на алфавит и посчитайте. Получается, что буква ё – никакая. Всех сосчитали, а её – нет. Как это может быть – непонятно. Уже этот факт говорит о том, что и словесникам неплохо бы знать математику. Поэтому, отбросив споры языковедов, возьмем за аксиому (как говорят математики), что в русском алфавите 33 равноправных буквы. Еще одно замечание касается названия буквы э. Иногда её называется просто э, а иногда э оборотное. Будем проще, то есть называть эту букву э.

В некоторых книгах приводится алфавит, в котором три буквы ъ, ы, ь написаны только маленькими и для них нет написания большой буквы [19]. Тем самым, наверное, хотят подчеркнуть, что эти буквы не могут стоять в начале слова. В «Этимологическом словаре русского языка» М. Фасмера особо указано, что буква ы никогда не может начинать слово. Действительно, твердый знак и мягкий знак не могут стоять в начале слова. Правда, при перечислении букв, мне пришлось поставить их в начале предложения. Как их нужно было написать? Сейчас на компьютерной клавиатуре эти знаки можно напечатать большими буквами и это правильное дополнение, ведь иногда заголовки статей в газетах, книгах набирают целиком большими буквами, чтобы выделить их графически. Относительно буквы ы появились примеры, опровергающие приведенные высказывания. Она может стоять в начале слова, это подтвердили поиски в различных словарях и географическом атласе. Например, в Туве существует село Ырбан, в Коми – гора Ыджыдпарма. У тюркских народов есть музыкальный жанр, который называется ыр. Вот вам эта буква в начале слова и прописная и строчная. Дело в том, что язык, как совокупность слов не является чем-то раз и навсегда зафиксированным. Различные народы общаются между собой, мировая цивилизация воспринимается как нечто единое, и происходит взаимопроникновение языков. Слова, возникшие в одном языке, заимствуются другими в результате глобальных общепланетных процессов. Река, протекающая где-то в Замбии, должна быть как-то названа в русском издании Атласа мира, это касается и названий городов, государств. Отдельные личности по результатам своей деятельности становятся общеизвестными и их имена включаются в энциклопедические словари других стран, следовательно, входят в различные языки. Пределом этого развития должно стать создание единого общепланетного языка землян. Подобные попытки делались, например, язык эсперанто, но они были искусственны. Русская поговорка гласит: «Насильно мил не будешь». Кроме географических названий, имен людей, незримый процесс глобализации языка идет в математике, химии, где ученые всех стран используют одинаковые знаки цифр, символы операций, знаки и формулы химических элементов и соединений. Математические и химические выражения уже стали общепонятны. Процесс идет!

Теория множеств и алфавиты

Школьным учителям-предметникам, нужно постоянно помнить о межпредметных связях и на своих уроках стараться показать единство человеческих знаний, а не их разобщенность по отдельным наукам. Например, изучение основ математической теории множеств можно успешно проводить, иллюстрируя введение новых понятий примерами из русского алфавита.

Множество – одно из основных, фундаментальных понятий математики, которое нельзя определить через другие понятия, поэтому его можно только более или менее доходчиво описать. Множество – это любое собрание определенных и различимых между собой объектов мыслимое как единое целое. Эти объекты называются элементами или членами множества. Существенно для понимания, что здесь собрание предметов само рассматривается как один объект. Множество деревьев – это сад или лес, множество учащихся – класс или школа, множество работников предприятия – коллектив, множество птиц – стая. Для обозначения множеств обычно используют большие латинские буквы. Множество может быть конечным, когда конечно число входящих в него элементов. Например, множество букв русского алфавита конечно и состоит из 33 элементов. С другой стороны, множество всевозможных упорядоченных наборов букв бесконечно, если не накладывать ограничений на длину этих наборов.

Конечное множество можно задать простым перечислением его элементов. Для этого принята следующая форма записи: R={а, б, в, г, д, е, ё, ж, з, и, й, к, л, м, н, о, п, р, с, т, у, ф, х, ц, ч, ш, щ, ъ, ы, ь, э, ю, я}.

Так мы задали множество букв русского алфавита. Определим подобным образом еще несколько конечных множеств, состоящих из тех же букв и собранных по некоторым индивидуальным для каждого множества признакам:

G={а, е, ё, и, о, у, ы, э, ю, я},

S={б, в, г, д, ж, з, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ},

P={й},

Z={ъ, ь},

D={б, в, г, д, ж, з, л, м, н, р},

T={к, п, с, т, ф, х, ц, ч, ш, щ},

X={ж, ш, ч, щ}.

Другой способ задания множества – описательный. Нужно сформулировать предложение, которое описывает данное множество так, что его нельзя спутать ни с каким другим и о любом объекте можно точно сказать принадлежит ли он этому множеству или нет. Тогда перечисленные выше множества букв будут определяться так:

G – множество гласных букв русского алфавита,

S – множество согласных букв,

P – множество полугласных букв,

Z – множество букв, которым не соответствует никакого звука в устной речи, иначе говоря – множество знаков,

D – множество звонких согласных,

T – множество глухих согласных,

X – множество шипящих согласных.

Бесконечное множество нельзя задать перечислением всех его элементов, но часто можно описать их свойства. Встречаются и конечные множества с той же степенью неопределенности. Например, до сих пор ученым не удалось расшифровать письменность острова Пасхи. До нас дошли несколько десятков табличек, покрытых рисуночными значками, вырезанными зубом акулы по дереву. Эти письмена аборигены называют кохау ронго-ронго – «говорящее дерево». Множество знаков-иероглифов в письменности острова Пасхи, можно определить этим предложением, но нельзя с уверенностью и точно перечислить, хотя это множество заведомо конечное.

Множества G, S, …, X содержат разное количество элементов и среди них есть одно, для которого используется специальное название. Множество, содержащее единственный элемент называется одноэлементным или единичным множеством. Речь идет о множестве P={й}, которое содержит единственную букву, обозначающую полугласный звук, то есть звук не образующий слога. Можно задать и пустое множество, в котором не содержится ни одного элемента. Так как это множество никак не характеризуется своими отсутствующими элементами, то логично утверждать, что может быть только одно множество, не имеющее элементов. Для его обозначения принят специальный знак Ø.

Отношения между объектами и множествами описываются понятием принадлежности. Для записи этого отношения есть два специальных знака принадлежит и не принадлежит.

означает, что буква а – гласная и является элементом множества гласных букв, то есть принадлежит ему.

означает, что буква а не является согласной и не принадлежит множеству согласных букв. В качестве сокращения можно записывать отношение принадлежности сразу для нескольких элементов:

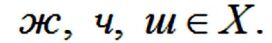
Отношения между множествами определяются следующими утверждениями.

Два множества равны в том и только в том случае, когда они состоят из одних и тех же элементов. Для обозначения равенства двух множеств применяется обычный знак равно {a, e, o}={e, o, a}. Порядок расположения элементов при их перечислении не важен, он не меняет состава множества.

Соответственно, два неравных множества отличаются, по крайней мере, одним своим элементом (X≠ {ж, ш, ч}).

Если каждый элемент множества А одновременно является элементом множества В, то говорят, что А включено в В или А есть подмножество множества В. Символически записывается:

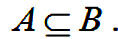
Выражение В содержит А является синонимом для выражения А включено в В.

Если одновременно выполняются два условия: А включено в В и А≠В, то говорят, что множество А строго включено в В или А есть истинное подмножество множества В

Пустое множество является подмножеством любого другого множества, то есть для любого множества А:

Знак включения как и знаки равенства и принадлежности имеет свое отрицание, которое выражается соответствующим перечеркнутым знаком, означающим, что А не является подмножеством множества В:

Применительно для ранее введенных буквенных множеств можно написать следующие утверждения:

Попробуйте самостоятельно дать им словесную формулировку.

Каждое не пустое множество (А≠Ø) имеет по крайней мере два различных подмножества: само А и Ø. Кроме того, каждый элемент множества А определяет некоторое подмножество множества А. Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается P(А).

Например, если С={у, р, о, к}, то P(С)= {С, {у, р, о}, {у, р, к }, {у, о, к}, {р, о, к}, {у, р}, {у, о}, {у, к}, {р, о}, {р, к}, {о, к}, {у}, {р}, {о}, {к}, Ø }.

Для конечного множества А, состоящего из n элементов, множество-степень P(А) содержит 2n элементов. Действительно, в предыдущем примере мы получили 24=16 элементов.

Множества – это математические объекты и над ними можно выполнять некоторые операции.

Объединением множеств А и В называется множество всех предметов, которые являются элементами множества А или элементами множества В. Обозначается:

Слово или в этом определении имеет не исключающий, а собирательный смысл. Например, если мы объединим множество глухих согласных и множество звонких согласных, то получим множество всех согласных букв:

Справедлива и такая запись:

Пересечением множеств А и В называется множество всех предметов, являющихся элементами обоих множеств А и В одновременно. Обозначается:

Среди звонких согласных есть только одна шипящая, буква – ж, а среди глухих три шипящих, поэтому:

Два множества называются непересекающимися, если у них нет общих элементов:

и пересекающимися, если

Множество гласных букв и множество согласных букв не имеют общих элементов – они непересекающиеся:

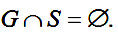
Дополнением множества А до множества В называется множество тех элементов множества В, которые не являются элементами множества А. Обозначается:

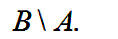
Дополнением множества глухих согласных до множества всех согласных будет множество звонких согласных:

Теперь попробуйте самостоятельно объяснить словами следующие символические записи и проверьте их правильность:

Для графической иллюстрации отношений, которые могут иметь место между различными множествами, часто используют так называемые диаграммы Венна. На этих диаграммах множества условно изображаются геометрическими фигурами с соблюдением отношений включения, пересечения и т. д.

В наших рассуждениях все рассматриваемые множества являются подмножествами по отношению к множеству всех букв русского алфавита R. В этом случае оно называется универсальным множеством, и его изображаем в виде прямоугольника, а все подмножества входящими в прямоугольник кругами. Непересекающиеся множества изображаются непересекающимися кругами, а включению множеств соответствует изображение одного круга целиком внутри другого. Для букв русского алфавита можно вычертить следующие диаграммы.

На первой диаграмме Венна показаны названия множеств, без состава их элементов, но с соблюдением отношений включения и пересечения. В данном примере самое большое множество, включающее в себя все остальные в качестве подмножеств – это множество всех букв русского алфавита. Далее даем подробную диаграмму без названий множеств, но с изображением конкретного состава элементов каждого из них.

Теперь с целью расширения кругозора и в качестве исходной базы для последующих упражнений введем еще несколько буквенных множеств, основанных на алфавитах других языков. Для простоты изложения будем рассматривать только маленькие (строчные) буквы. Возьмем уже известную нам латиницу L={a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, x, y, z}. Следующее множество А определим как множество букв английского алфавита, а уж вы сами вспомните какие буквы в него входят и сколько их [?]. Еще два множества – алфавиты бывших союзных республик, имеющих разную ориентацию: эстонский алфавит создан на основе латинского (Эстония всегда ориентировалась на Запад), и казахский алфавит, созданный на основе русского.

В эстонском алфавите 23 основных буквы, которые употребляются для передачи слов родного языка, и 9 букв (f, š, z, ž, c, q, w, x, y) используемых только в недавних заимствованиях из других языков и иноязычных именах собственных.

E={a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, š, t, u, v, w, x, y, z, ž, ä, õ, ö, ü}.

В казахский алфавит полностью входят 33 буквы русского алфавита, три буквы из латинского алфавита (ү, h, i) и шесть своеобразных букв (ə, ғ, қ, ң, ө, ұ), – всего 42 буквы.

К={а, ə, б, в, г, ғ, д, е, ё, ж, з, и, й, к, қ, л, м, н, ң, о, ө, п, р, с, т, у, ұ, ү, ф, х, h, ц, ч, ш, щ, ъ, ы, i, ь, э, ю, я}

[?-1]

Определите множества, которые получатся в результате следующих операций:

Примечание: В данном упражнении нас интересует только графическая сторона вопроса. Если рассматривать алфавиты так, как они записаны здесь – маленькими буквами, то у русского и латинского алфавитов есть одинаковые знаки: а, с, е, …, поэтому их пересечение не является пустым множеством.

[?-2]

Верны ли следующие утверждения:

[?-3]

Постройте диаграммы Венна для следующих множеств, считая универсальным множество всех алфавитов:

В процессе работы над книгой меня постоянно волновал вопрос: кому это будет нужно? Учитель-словесник отмахнется от математики, зачем ему теория множеств, учитель математики отмахнется от букв, алфавитов, слов, потому что ему всегда удобнее объяснять материал на числах и получится мой труд ради собственного удовольствия. Изрядную долю сомнений вносили знакомые учителя, зачастую именно так и высказываясь. Но меня не покидает надежда, что молодое поколение учителей будет мыслить по-другому, шире и разностороннее. Ученикам никогда не будет интересна нудная, хотя и необходимая, зубрежка правил, и, чтобы не отбить окончательно у них желание учиться, нужно использовать любую возможность сделать свой предмет увлекательным. Кому станет хуже, если на математике ученики повторят русский алфавит, распределение его букв по видам, узнают новые алфавиты.

Топология букв

Еще немного чистой математики, причем не изучаемой в школе, применительно к языковому исходному материалу. Посмотрим на буквы с точки зрения топологии.

Топология (греч. topos – место и logos – слово, понятие, учение) – раздел математики, изучающий наиболее общие свойства геометрических фигур (свойства, не изменяющиеся при любых непрерывных преобразованиях фигур).

Представьте себе, что большие печатные буквы сделаны из гибкого и растяжимого материала, например из проволоки, и их можно распрямлять, растягивать, выводить из плоскости, переворачивать и переносить в другое место. Подобные преобразования называются топологическими. Две буквы называются топологически эквивалентными, если их можно перевести друг в друга такими непрерывными деформациями (не разрешается разрезать или склеивать буквы!). Например, возьмем проволочную букву Г, из нее легко можно сделать буквы С или П, распрямив и согнув по-другому, но нельзя сделать букву О, для этого проволоку нужно спаять или склеить, а эта операция запрещена. По признаку топологической эквивалентности все буквы можно разбить на несколько классов. Буквы Г, З, И, Л, М, П, С относятся к простейшему классу, распрямив, их можно все превратить в отрезок прямой ________. Если распрямить буквы Е, Т, У, Ц, Ч, Ш, Э получатся три отрезка, спаянные одним концом в общей точке и так далее.