Физические основы теории роупджампинга

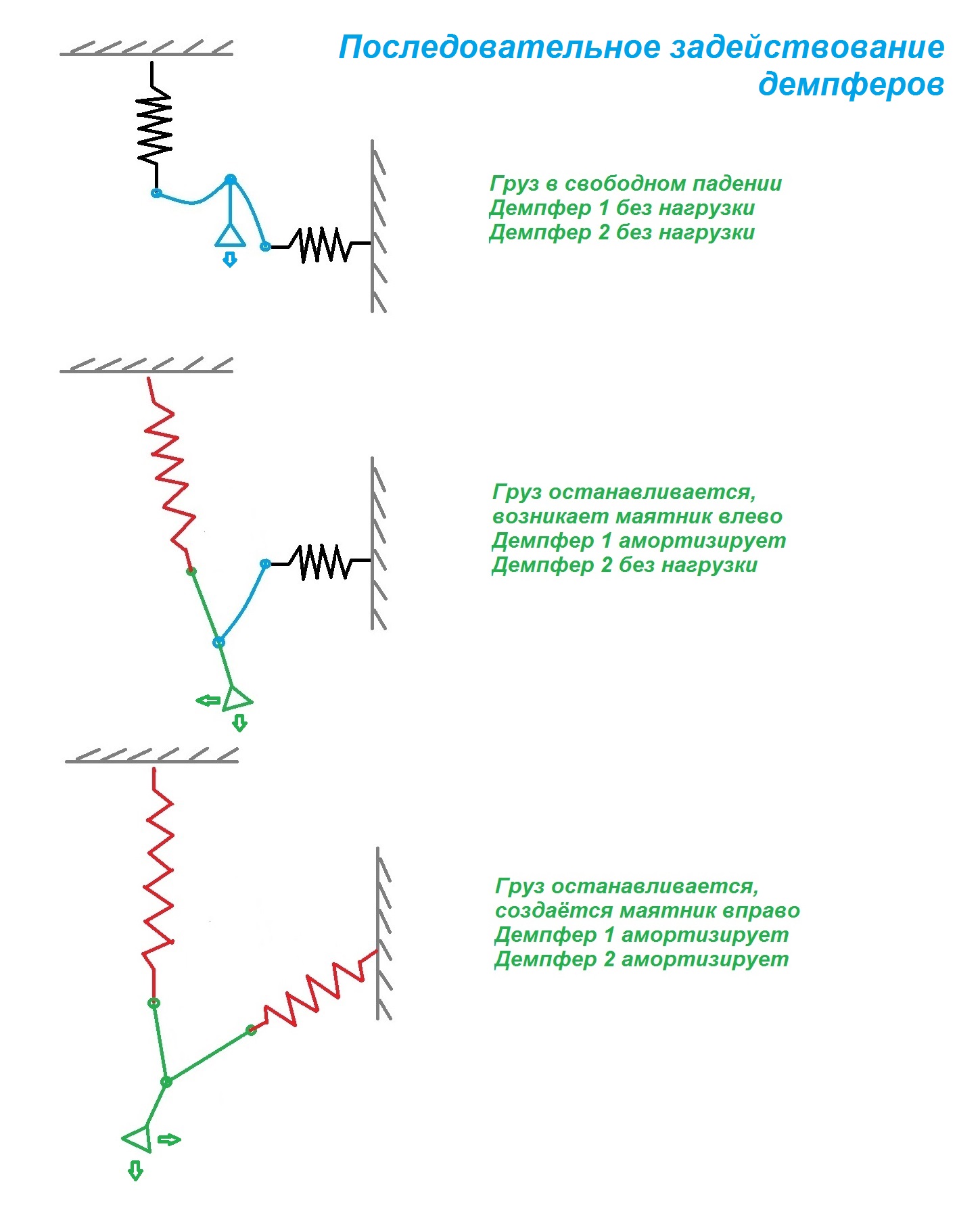
Для описания порядка соединения введем понятие: направление демпфера. Демпфер имеет два конца, и от одного к другому, вдоль него, действует сила упругости. Конец, от которого действует сила, – это вход. А тот, к которому действует – это выход.

Соединение указывает на вид механической связи между элементами: последовательно – это когда выход одного демпфера прикреплён ко входу другого; параллельное соединение – это когда входы элементов скреплены между собой, и выходы этих демпферов соединены аналогично.

Задействование же раскрывает временной момент вступления демпферов в амортизацию: последовательно – это один элемент после другого; параллельно – это одновременно.

Понятие комплексной композиции

После реализации системы остановки свободного падения зачастую выявляется какое-нибудь одно наиболее удачное свойство, а другие далеко не всегда выдающиеся. Например, большая упругость или значительный маятник, малая перегрузка или удобство спуска. И для нового решения подход к организации торможения прыгуна возможен с заранее заложенным набором таких свойств. Что наиболее просто выполнимо, если объединять системы целиком, и использовать их как готовые структурные демпферы в общем наборе амортизаторов. Этот метод создания называется комплексной композицией систем.

В качестве примера такого создания предлагается комплексная троллейная система. В ней объединена троллейная комбинированная система и перпендикулярная система V-плеч. Удачным свойством троллейной системы принимается быстрая «доставка» анкерного устройства страховочной системы в оптимальную зону перпендикулярной амортизации. Особенно, при значительных углах наклона и слабом значении предварительного натяжения. Перпендикулярный демпфер ценен своей подвижностью, особенно на небольших отклонениях от предварительного натяжения.

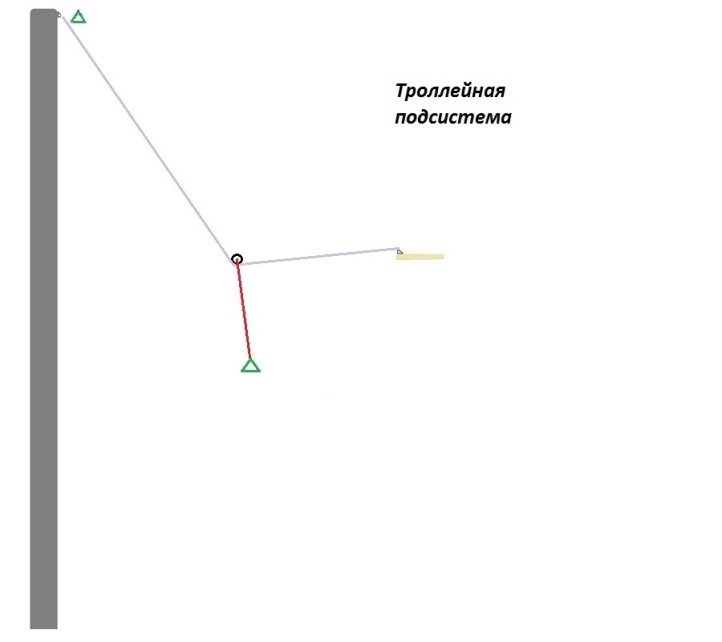
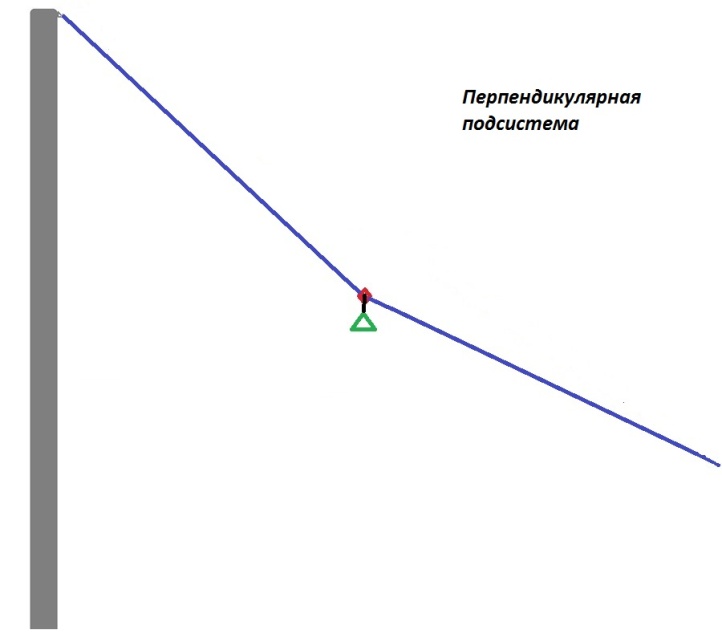
Объединение производится через внедрение троллея в верхнюю часть наклонного перпендикулярного демпфера. Для сохранения упругих свойств подсистемы перпендикулярной амортизации верхняя часть комплексной системы, объединяющая троллей и верхний фрагмент линии перпендикулярной амортизации, должна иметь модуль продольной упругости (Юнга) равный значению одинарного нижнего фрагмента перпендикулярной амортизации.

Технически, если одну линию надо заменить на две таких же, не меняя общую жёсткость фрагмента, следует в два раза увеличить их длины, а вместо анкерной точки замещаемого фрагмента установить блок-ролики. С одновременным созданием анкерных точек после роликов на удалении, равном заменяемому фрагменту. Подобная операция называется расщеплением жёсткости.

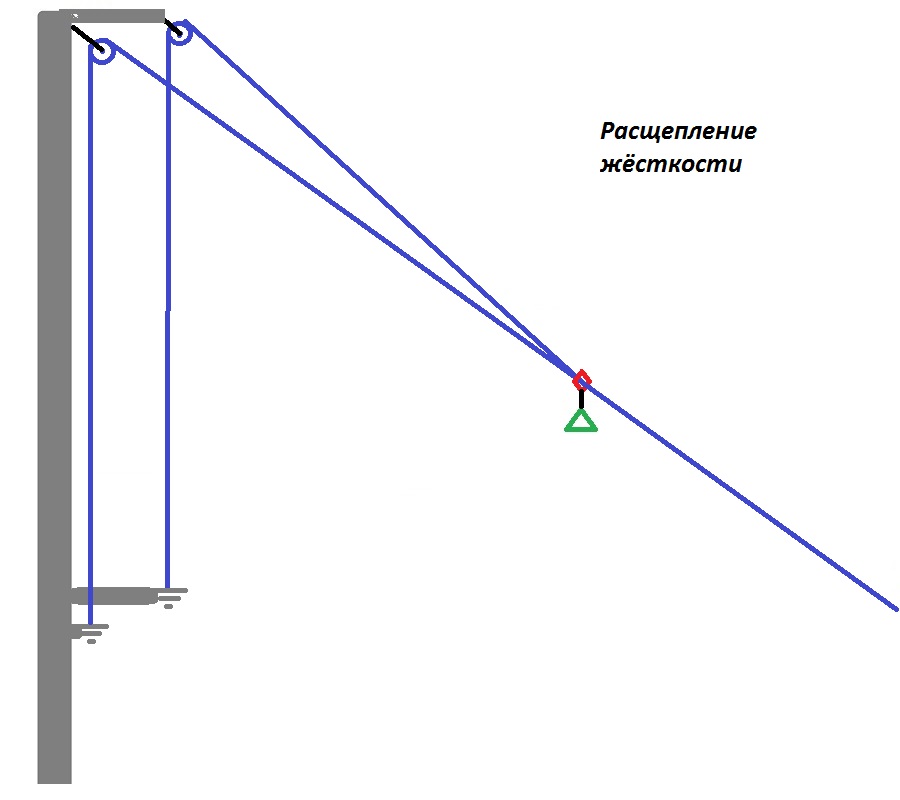
Выполним расщепление жёсткости верхнего фрагмента демпфера перпендикулярной амортизации. Нижнюю линию организуем в качестве троллейной комбинированной системы. Теперь нижняя анкерная точка наклонного троллея имеет фиксированное динамическое размещение. Причём, в точке оптимальной перпендикулярной амортизации V-подсистемы. И пусть все расстановки удовлетворяют безопасности по факторам запаса высоты и маятника. Соотношения длин, масс и коэффициентов упругости подсистем будут обеспечивать апериодический переходный процесс (когда не будет «подскакивания» выше уровня предварительного натяжения ни ролика, ни опорной точки второй анкерной линии во время съезда).

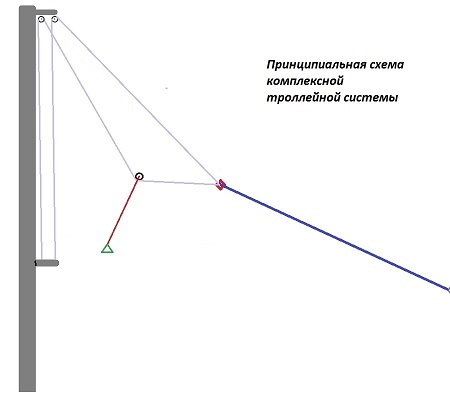
Общее рассмотрение динамики новой системы указывает на бОльшие амортизационные свойства, чем в каждой из объединяемых систем отдельно. Троллейная система становится «мягче» на анкерной линии с уменьшенной жёсткостью. А перпендикулярная V-система создаёт «плавающее» основание для троллея, что дополнительно увеличивает глубину остановки падения и «смягчает» остановку ролика. Этот пример обосновывает целесообразность комплексного проектирования.

Анализ ударного воздействия

Явление удара возникает при взаимодействии макроскопических тел с быстрым изменением скорости за очень короткий промежуток времени. Вследствие значительного изменения скорости от ударяемого тела к ударяющим передаются большие ускорения, направленные противоположно ударяемому телу. Как следствие, передаются и большие силы инерции, вызывающие существенные напряжения во взаимодействующих телах.

С точки зрения биомеханики человек представляет собой звеньевую систему. Периферические звенья, в общей массе, приблизительно равны массе центральных звеньев – туловища. Когда система остановки падения через страховочную обвязку, сблокированную на центральных звеньях, воздействует на прыгуна, центральные звенья сжимаются обвязкой, а периферические звенья увлекаются вслед упругими связями сухожилий и мышц. Чем быстрее ускоряется центр масс, тем сильнее нагружаются связи, вследствие инертности звеньев. Существуют предельные переносимые человеком значения растяжений и сдавливаний в связях. Чем меньшие силы инерции возникают в человеке, тем «мягче» он ощущает торможение, воспринимая его только через увеличение собственного веса (перегрузку) без разрушающих биомеханическую конструкцию внутренних напряжений.

Само описание траекторий движения звеньев и сил между ними сложно из-за существенного вклада внутренних колебательных степеней свободы. Поэтому в решении инженерных задач широко используются обобщённые энергетические характеристики взаимодействия. Для этого удобно использовать понятие механической мощности.

Когда на движущееся тело действует сила, то она совершает работу. Скалярное произведение вектора силы на вектор скорости характеризует скорость совершения работы этой силой и является мощностью N:

,

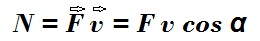
где α – угол между векторами силы F и скорости v.

В анализе движения различают мгновенную w(t) и среднюю W(T) мощность.

Мгновенная мощность в текущий момент времени отображает состояние развития воздействия через точку приложения силы и равна:

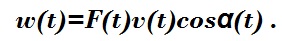
Средняя мощность вычисляется отношением интеграла мгновенной мощности за характерный промежуток времени T к величине этого промежутка:

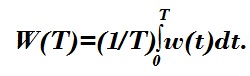
Определим переменные для вычисления мощности нагрузки на прыжковую систему.

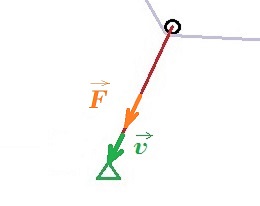
В соответствии с Третьим законом Ньютона, сила нагрузки F(t) численно равна силе натяжения линейного демпфера, подсоединённого к прыгуну, и противоположно направлена ей. По закону Гука сила упругости противоположно направлена деформации, а значит, и скорости её изменения. Следовательно, нагрузка сонаправлена скорости деформации. Таким образом, косинус α равен значению 1.

Параметр v(t) равен скорости изменения длины линейного демпфера.

Поэтому когда значение мгновенной мощности w(t) положительно – это отображается нарастание воздействия прыгуна на систему остановки падения и, одновременно, нарастание реакции системы на спортсмена.

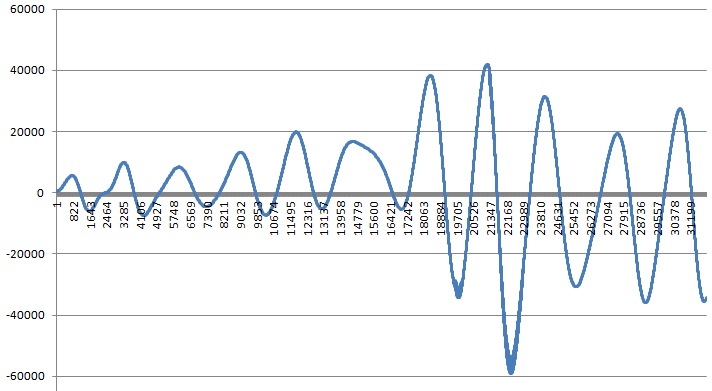
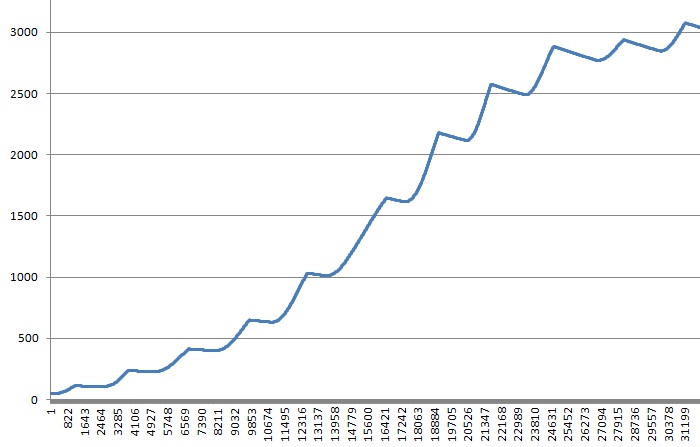
На рисунке изображён смоделированный расчет мгновенной мощности воздействия прыгуна на комбинированную блочную систему для объекта высотой 88 метров. Суммарный вклад ударной нагрузки вносят только положительные значения мгновенной мощности: только значения

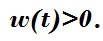
Анализ взаимодействия осуществляется через нахождение средней ударной мощности на положительных интервалах значений w(t) в течение остановки падения.

При наличии нескольких интервалов сперва выполняют усреднение мощности в течение каждого интервала для уменьшения осцилляций итоговой кривой при анализе.

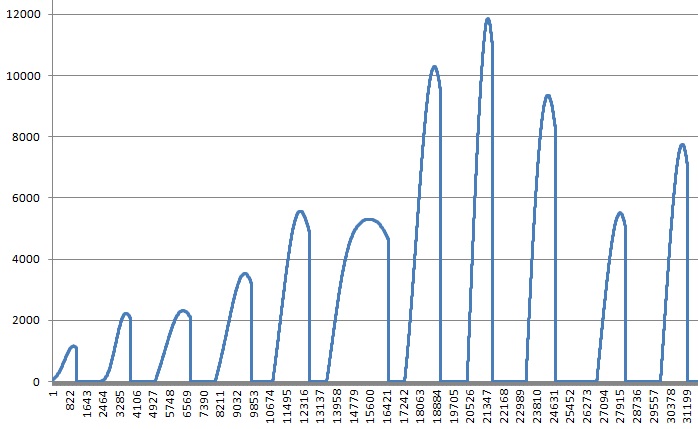
А потом, используя проведённое преобразование, последовательно усредняют результат в течение всего интервала торможения

T

.

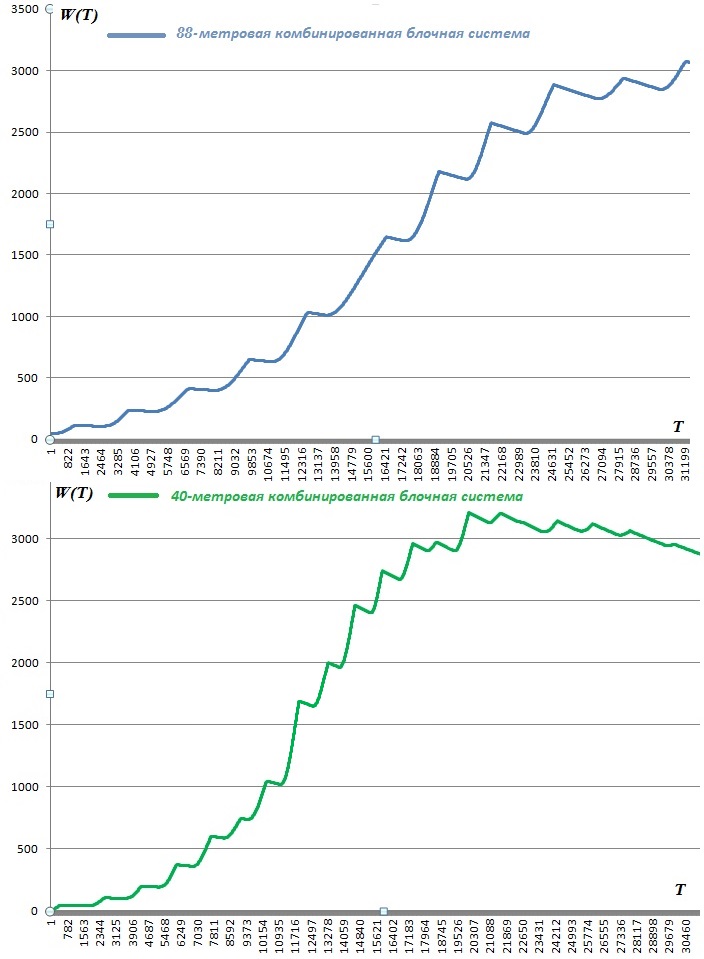
Получившаяся кривая средней мощности W(T) характеризует степень ударного воздействия через крутизну наклона. Чем быстрее нарастает кривая – тем сильнее ударное воздействие. Более пологая кривая указывает на меньшие внутренние напряжения у спортсмена при остановке падения. Не вдаваясь в математические методы оценки, графическое представление позволяет просто сравнивать прыжковые системы, если отобразить их кривые средней мощности на одной координатной плоскости в одинаковом масштабе.

Пример на рисунке показывает, что торможение блочной комбинированной системой с высоты 88 метров будет «мягче» восприниматься человеком по сравнению с установленной подобной системой на объекте высотой 40 метров вследствие бОльшей пологости кривой средней мощности нагрузки. При том, что значение максимальной перегрузки в обоих случаях составило 40 м/с².

Необходимость исследования спроектированных прыжковых систем

Как и во всяком инженерном строительном решении, при создании новой прыжковой системы изначально требуется выполнить технический расчёт. Затем осуществляется предварительное проектирование, результатом которого становится первообразное решение задачи остановки падения. Оно представляет собой готовый к монтажу вариант системы в полностью описанных элементах, включающих массогабаритные характеристики.

Полное аналитическое описание торможения верёвками громоздко и сложно к применению в практическом смысле. Поэтому предлагается комбинированный подход с использованием упрощённого описания элементов. Для них принимаются во внимание только главные свойства, причём набор этих качеств может отличаться в зависимости от размеров и условий эксплуатации оригинала.

С одной стороны, надо принимать во внимание девиацию (разброс параметров) реальных характеристик элементов, а также возможность значительного влияния неучтённых качеств. С другой стороны нахождение в системе человека, как самого ценного и непредсказуемого элемента. И, собственно, сама стоимость оборудования имеет не малую величину. Поэтому моделирование первообразной системы, а затем исследование модели и систематизация данных о её «поведении» представляет собой важнейший этап на пути профессионального разработчика.

С учётом полученных данных корректируется исходный проект. Или вносятся изменения в модель. Или регистрируется достаточность соответствия, что дает проекту путёвку на тестовое создание оригинала.

Технология моделирования включает в себя более двух десятков разновидностей. Применительно к роупджампингу, мы посчитали достаточными для проектирования три вида. Компьютерное моделирование с численным и графическим выводом, формальное информационное моделирование на базе таблиц Excel и физическое моделирование.

Компьютерное моделирование на примере комбинированной двукратной полиспастной прыжковой системы

Исследование достаточности упрощённого описания в компьютерном моделировании проводили на действующей прыжковой системе. Комбинированная двукратная полиспастная система предполагает фиксированное размещение одинарных блоков на гибких анкерных линиях. Через них пропущен линейный демпфер – двойная верёвка. Одним концом верёвки соединены с прыгуном, другим концом – с анкерными точками. Линейный демпфер представляет собой одновременно и поводок, и стопор.

Для упрощения аналитического описания, прыжковая система была представлена набором материальных точек, связанных между собой линейными структурными демпферами с постоянными значениями модулей продольной упругости. Также было принято решение о рассмотрении двумерной модели, ибо самые важные вопросы исследования мы связывали с высотами, скоростями, силами натяжений и перегрузками. Коридор маятника на этом этапе был исключен из рассмотрения.

В программе моделирования производится непрерывное численное интегрирование координат двух материальных точек, соответствующих прыгуну и креплениям блоков-роликов. При этом учитывается аэродинамическое сопротивление роупджампера по значению текущей скорости и положению в пространстве.

В расчете ускорений определяющими, кроме ускорения свободного падения, выступают, во-первых, силы упругости, возникающие при удлинении демпферов (двойных верёвок). А во-вторых, значения массы, сосредоточенные в материальных точках. Предполагалось также, что для высот до 100 метров инерция верёвок не потребует усложнённой сегментной реализации в модели.

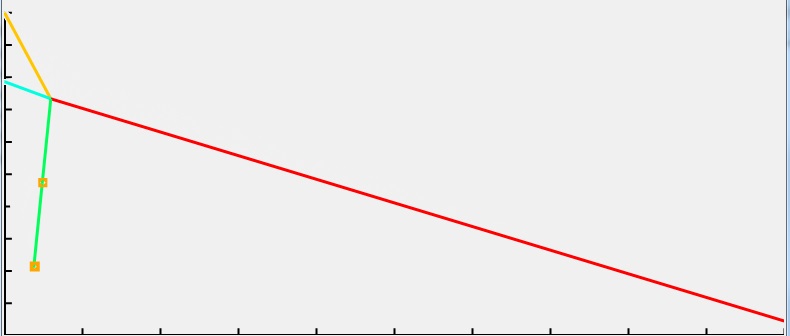
Рисунок представляет собой кадр из видео-ролика отображения работы модели. Цвета означают силы натяжения: чем краснее, тем сильнее. Результат моделирования, после сравнения с реальной системой, подтвердил достаточность упрощения.

Таким образом, появилась возможность исследования параметров прыжковой системы. И, наконец, позволило определить оптимальные диапазоны сил натяжения анкерных линий, геометрические размеры и размещения элементов, предельные нагрузки и глубины падения. А также эта модель использовалась для определения меры ударного индикатора нагрузки.

Формальное информационное моделирование

Составление компьютерной модели имеет дело с мгновенными характеристиками амортизации прыжка: силами, координатами, скоростями, углами. По трудоёмкости значительно, а по анализу сложно: нужно сравнивать большое множество получаемых данных, которые надо выводить в графической и цифровой форме одновременно.

Поэтому. Для оценки разнонаправленных неоднородных процессов, особенно в потенциальных полях сил (коими являются как сила тяжести, так и силы упругости) применяется энергетический метод. Суть его состоит в том, что, с некоторыми ограничениями, сумма потенциальной и кинетической энергии остаётся неизменной.

Итак, зафиксировав конструкцию системы, математически находят взаимно однозначное соответствие между растяжениями демпферов системы. Потом создают таблицу эксперимента, где для каждого набора упругих деформаций рассчитаны силы и работы, обеспечивающие данное состояние системы. А также рассчитана суммарная работа элементов и перегрузка в демпфере прыгуна.

Определив массу прыгуна и задав глубину падения, определяем скорость до начала торможения (здесь один раз, предварительно, составляется таблица методом математического моделирования: масса – глубина падения – скорость). Далее фиксируем значение кинетической энергии прыгуна в начале торможения. В таблице находим ближайшую строчку, где значение полной работы амортизации больше полной энергии прыгуна. Это процедура и есть испытание формального информационного эксперимента. Именно таким образом мы в нашей книге исследовали базовые структурные демпферы.

Строчка эксперимента сразу показывает деформации, силы и распределение энергий в элементах, которые образуются в точке остановки падения. Таким образом, становится ограниченным для исследователя диапазон изменения системы. А при допустимых значениях сил и перегрузки можно переходить к анализу фактора маятника.

Физическое моделирование

Кинематическая сложность траектории объектов при действии не постоянных во времени и по направлению сил ни у кого не вызывает сомнения. Поэтому создание компьютерной модели для оценки маятниковых движений обоснованно занимает значительный промежуток времени. Если рассматривать эффективность разработки системы, то, при полученных удовлетворительных результатах информационного моделирования, гораздо проще и быстрее воспользоваться методом физического моделирования. В нашем случае он состоит в эксперименте на уменьшенном оборудовании с последующим воспроизведением записанного процесса в, соответствующем уменьшению размеров, отмасштабированном временном виде. Задача состоит в том, чтобы наблюдать траекторию груза в модели как реальный процесс: временные рамки прохождения траектории в модели и оригинале должны совпадать. Уменьшив в модели высоту и жёсткость демпферов, следует соответственно уменьшить и массу груза модели. Вывод этого коэффициента преобразования разберём на примере.

Пусть моделирование проведём на тонкой одинарной верёвке диаметром 2 мм, эквивалентной сбросу тестового груза на одинарной верёвке диаметром 10 мм. Условно предположим для обеих верёвок одинаковые модули Юнга. Соотношение площадей сечения одной 10 мм верёвки и одной мм верёвки, в таком случае, будет равно коэффициенту уменьшения жёсткости Kж, пропорциональному уменьшению площадей сечения. Kж = (10*10) / (2*2) = 25. А масштаб уменьшения по высоте возьмем, для примера, Kh = 10.

По закону сохранения энергии, без учета сопротивления воздуха, приобретённая грузом кинетическая энергия равна потенциальной энергии запаса высоты до начала торможения:

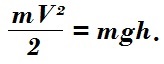
Таким образом, приобретённая скорость V связана зависимостью квадратного корня от высоты пролёта груза h

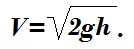
Поэтому уменьшение высоты h в модели в Kh раз изменит приобретённую скорость Vмодели:

Итак, коэффициент уменьшения приобретённой скорости Kскорости составляет:

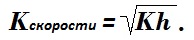
Система до начала торможения находится в покое и получает кинетическую энергию груза на амортизацию. Под её воздействием система деформируется, поглощая и её, и нарастающую потенциальную энергию груза до остановки. Уравнение закона сохранения энергии для системы выглядит так:

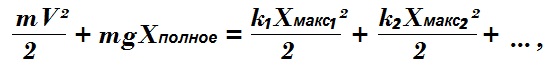
где Xполное – это глубина падения груза от начала взаимодействия до момента остановки падения;

Xмакс₁, Xмакс₂, … – максимальные деформации линейных фрагментов системы в момент остановки;

k₁, k₂, … – коэффициенты жесткости линейных фрагментов системы.

Изменение в модели приобретённой грузом скорости в Kскорости раз для сохранения равенства должно привести к изменению с одинаковым коэффициентом каждого слагаемого уравнения закона сохранения энергии:

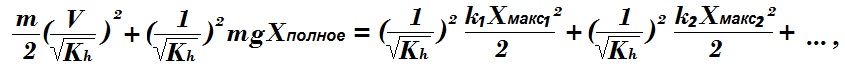
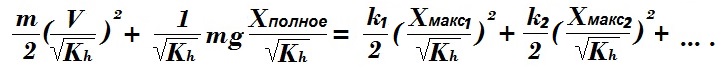
Учтём уменьшение в модели жёсткости в Kж раз. Аналогично требуется деление каждого слагаемого уравнения системы этот коэффициент:

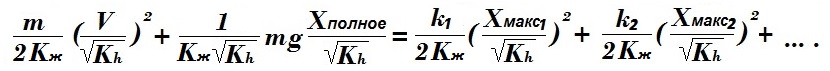
Параметры Vмодели, Xполное модели и все Xмакс модели все стали меньше с одинаковым коэффициентом:

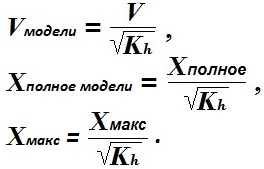
Далее в получившемся уравнении сохранения энергии заменим массу груза на массу модели, используя коэффициент массы уменьшения Kмассы у слагаемого потенциальной энергии:

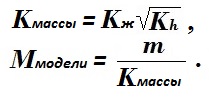
Для модели с такими параметрами запишем получившееся уравнение закона сохранения энергии:

Итак, в граничном положении остановки падения модель будет геометрически подобна первообразной системе, поскольку и деформации элементов подобны, и глубина падения, и потенциальная энергия в момент остановки падения подобны оригиналу. А вот кинетическая энергия модели в момент остановки будет для такой массы увеличена в Kскорости раз от подобного значения оригинала. Поэтому для анализа кинематики движения нужно уменьшение масштаба времени в соответствующее число Kскорости раз. Это можно выполнить либо увеличив массу в Kскорости раз – но такие растяжения не выдержат верёвки модели. Либо, записав на видео процесс, с помощью программ обработки видео, а затем воспроизвести его замедленно.

В нашем примере высота была уменьшена в Kh = 10 раз, соответственно, воспроизведение надо замедлить в Kскорости = 3,16 раза.

Также рассчитаем в примере коэффициент уменьшения массы Kмассы, который в соответствии с преобразованиями равен произведению коэффициента уменьшения жёсткости демпферов на коэффициент уменьшения скорости Kскорости:

Kмассы = 25* sqrt (10) = 79 раз. Это, для моделирования сброса нашего тестового груза 140 кг, дает массу груза модели Mмодели:

Mмодели = 140 / 79 = 1,77 кг.

Что касается значений сил упругости в модели, то, по закону Гука, они изменятся в соответствии с изменением коэффициента уменьшения жесткости Kж: