Физические основы теории роупджампинга

Прыжок

Чем обладает прыгун на высоте, и что он обретает после отделения от помоста, кроме незабываемых эмоций?

Энергия. Высота обеспечивает запас потенциальной энергии. И часть её с каждым мгновением падения преобразуется в кинетическую.

Чем дольше падение, тем больше значение кинетической энергии, прыгун получает импульс.

В состоянии свободного падения на человека действуют две основные силы: сила притяжения Земли и сила сопротивления окружающей среды – воздуха.

С определенного момента для остановки падения прыгуна добавляется действие системы уменьшения приобретенного импульса.

Способы остановки падения

Торможение свободного падения может происходить двумя способами, действующими одновременно или раздельно.

Первый способ состоит во взаимодействии с окружающей средой объекта торможения – в нашем случае с воздухом. Второй способ в переводе кинетической энергии объекта в потенциальную энергию сопряженных с ним элементов, причем как упругими деформациями, так и трением.

Первый способ в большей мере применим для парашютного спорта, прыжков в воду.

Второй способ одной из возможностей приводит нас к созданию веревочных систем остановки падения, давших начало экстремальному виду спорта – прыжкам с верёвкой или роупджампингу.

Комбинированный метод изучения

Решение задач действия непостоянных во времени сил (упругих деформаций и аэродинамических сопротивлений) принципиально может быть получено через решение систем дифференциальных уравнений. Общий вывод и анализ этих решений сложен как в научном, так и в практическом рассмотрении.

Именно этим определялось предыдущее плачевное состояние в теории и, как следствие, в безопасности.

Поэтому за основу был принят комбинированный подход. Аналитические данные в этой сфере получаются, в большинстве случаев, симбиозом двух методов: численного математического моделирования и частными физико-математическими решениями с упрощающими ограничениями.

Главным образом, модель создаётся из рассмотрения системы материальных точек во взаимодействии, в соответствии с законами Ньютона. А после выполняется численное интегрирование. Результаты представляются как в графическом, так и численном виде.

Импульс

До принятия решения о параметрах необходимой системы торможения следует определить, каким импульсом будет обладать прыгун в начале остановки.

Здесь на первое место выходит противоборство силы тяжести и силы аэродинамического сопротивления воздуха.

Экспериментально установлено, что сила сопротивления зависит от скорости движения: чем больше скорость, тем больше сила. При движении в воздухе эта сила пропорциональна квадрату скорости с некоторым коэффициентом сопротивления, который зависит от различных параметров:

Поскольку, для высот до 250 метров спортсмен не развивает равновесной скорости падения, определение значения скорости свободного падения происходит методом математического моделирования. На высотах от 15 до 300 метров она в диапазоне от 12 м/с до 50 м/с. Ниже данные моделирования для прыгуна массой 100 кг, показывающие достижение скорости свободного падения после пролёта определённой высоты:

Произведение массы тела на скорость и представляет собой импульс, а половина произведения массы на квадрат скорости – кинетическую энергию, которые нуждаются в «гашении».

Чем длительнее будет его «гашение», тем меньше будет сила торможения (в соответствии с импульсной формулировкой Второго закона Ньютона), а, значит, и нагрузки: как на систему, так и на человека.

Оценить длительность торможения без специального оборудования сложнее, чем выполнить оценку длины траектории торможения.

Работа системы по остановке падения A определяется как интеграл скалярного произведения вектора равнодействующей сил торможения в точке траектории F(S) на вектор бесконечно малого перемещения dS в этой точке.

A = ∫ dA = ∫ F(S)*dS.

Чем длиннее будет траектория основного действия сил, тем меньшими их значениями может быть выполнена работа. Следует отметить, что при определённых условиях, главное действие сил может быть осуществлено на коротком участке общей траектории остановки падения, а на основном участке пути почти отсутствовать. И тогда силы торможения останутся велики даже при длинной траектории.

Глубина остановки и максимальная перегрузка в линейной системе

Рассмотрим идеальный случай остановки падения веревкой, жестко закреплённой одним концом, а другим концом подсоединённой к прыгуну – торможение линейной системой. Пусть остановка происходит только за счет упругой деформации, изменяющейся по закону Гука и без учёта сопротивления воздуха.

Сила по ходу торможения не постоянна, она возрастает по мере растяжения упругого элемента с коэффициентом жесткости k, и, очевидно, будет максимальной Fм при максимальном растяжении Xм.

Рассчитаем, какая максимальная перегрузка возникает при таком торможении.

По закону сохранения энергии работа силы упругости по остановке падения равна сумме двух энергий: приобретённой прыгуном кинетической энергии до начала остановки падения плюс запасу потенциальной энергии спортсмена от высоты начала торможения до высоты его завершения:

Отсюда, по Второму закону Ньютона, максимальное ускорение равно:

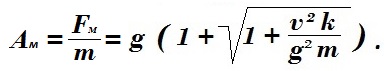
Теперь найдем максимальный коэффициент жёсткости k для максимально допустимого ускорения Aм в точке остановки падения:

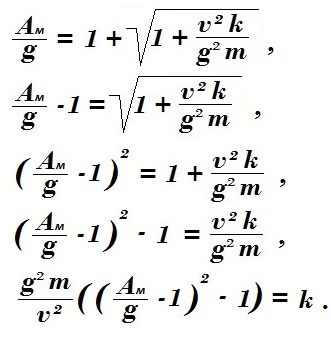
Для альпинистской практики комиссия УИАА пределом таких нагрузок дает порог не выше 400 кгс :=: 3920 Н, даже при наличии комбинированной системы обвязки. Что при массе m=100 кг дает значение 40 м/с2 (а при массе m = 70 кг, соответственно, 56 м/с2 ) .

Например, для скорости 20 м/с коэффициент жёсткости k будет равен:

k = (9,81²)*100/(20²)*((40/9,81-1)²-1)=204 Н/м.

Значение максимальной перегрузки G равно отношению максимальной силы торможения, приложенной к прыгуну, к весу прыгуна:

Таким образом, есть два важных вывода. Первый – это минимальное значение перегрузки для любой линейной системы равно 2. Второй вывод говорит об обратной нелинейной зависимости перегрузки от массы прыгуна m, при определённой достигнутой скорости v до начала торможения: чем больше масса, тем меньше перегрузка.

Значение максимальной перегрузки, которое наиболее часто используется как критерий предельного внешнего воздействия, является необходимым, но не достаточным условием для определения безопасной нагрузки на спортсмена. Практика также доказывает этот факт при сравнении разных систем остановки свободного падения или сравнении систем одного типа, спроектированных для разных высот прыжка на одинаковые значения максимальных перегрузок.

Объяснение этого связано с рассмотрением торможения как быстрого неравноускоренного взаимодействия страховочной системы и человека, которое включает биомеханику ударного контакта. Для анализа такого процесса требуются более сложные механические параметры, чем просто максимальное ускорение. В дальнейшем это явление будет разобрано как углублённое исследование критерия безопасного торможения.

Оценка длины тормозящей верёвки линейной системы

Закон Гука через модуль Юнга имеет такой вид:

.

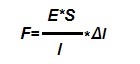
Коэффициент жёсткости k при таком написании вычисляется как:

.

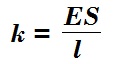
Подставив в уравнение максимального коэффициента жёсткости k для максимально допустимого ускорения Aм, получим:

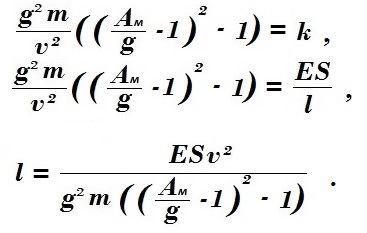
Предположим торможение динамической веревкой, жестко закреплённой одним концом, без учета сопротивления воздуха.

Установим параметры для динамической веревки 10 мм:

E = 200 МПа,

S = 0, 00008 кв м.

Определим, какова должна быть длина этой веревки l при заданном значении максимального тормозящего ускорения Aм=40 м/с². Для остановки падения прыгуна массой m=100 кг со скорости v=20 м/с понадобится такая минимальная длина одинарной динамической верёвки:

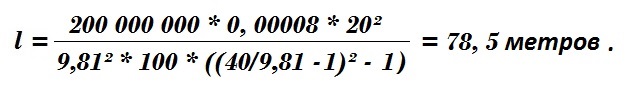
Сводная таблица основных параметров линейной системы

Для практического применения, после выбора веревки торможения, удобно представить расчетные данные в общей таблице. Они позволят правильно на конкретном объекте построить систему остановки падения.

Во всех системах канатного доступа для работы на высоте используется принцип дублирования, и прыжки с верёвкой не исключение. Поэтому человек должен быть подсоединён к прыжковой системе двумя верёвками. Штатное торможение осуществляется двумя верёвками. Но в случае выхода из строя одной, торможение будет выполнено с помощью оставшейся другой верёвки. Что обязательно принимать в рассмотрение для построения системы остановки падения.

Таким образом, введём параметры: полная глубина падения и предельная глубина торможения. Полная глубина падения (штатная) получается из суммирования глубины свободного падения и расчётной глубины торможения X2S. Предельная глубина торможения (аварийная) определяется из суммирования глубины свободного падения и расчётной глубины торможения XS для одной верёвки вместо двух.

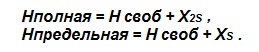
Выразим в формуле максимального растяжения Xм коэффициент жёсткости k через модуль Юнга:

Одна верёвка вместо двух соответствует уменьшению площади S в два раза. Поэтому подставим в формулу максимального растяжения Xм значения площадей S и 2S:

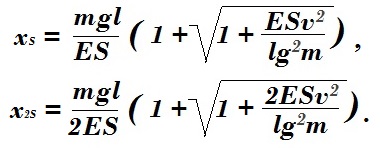
Из формулы максимальное растяжение для меньшей площади сечения увеличится в соответствии с пропорцией:

.

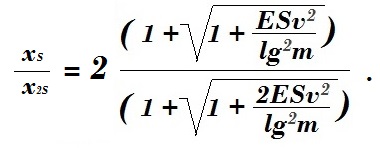
Возьмем, для примера, двойную динамическую веревку 10 мм. Один конец пары верёвок жёстко закреплён.

E = 200 МПа,

S = 2*0, 00008 = 0,00016 кв м, – двойная.

Масса прыгуна m = 100 кг.

Максимальная сила перегрузки Fм = 3920 H.

Итак, для заданных параметров рассчитаем длину требуемой двойной верёвки торможения l при разных достигнутых скоростях и соответствующих им глубинах завершения свободного падения без учёта сопротивления воздуха в процессе торможения. Далее определим глубины торможения: штатную X2S и аварийную XS. И, наконец, получим предельную расчётную глубину торможения Hпредельная. Полученные данные представим в таблице.

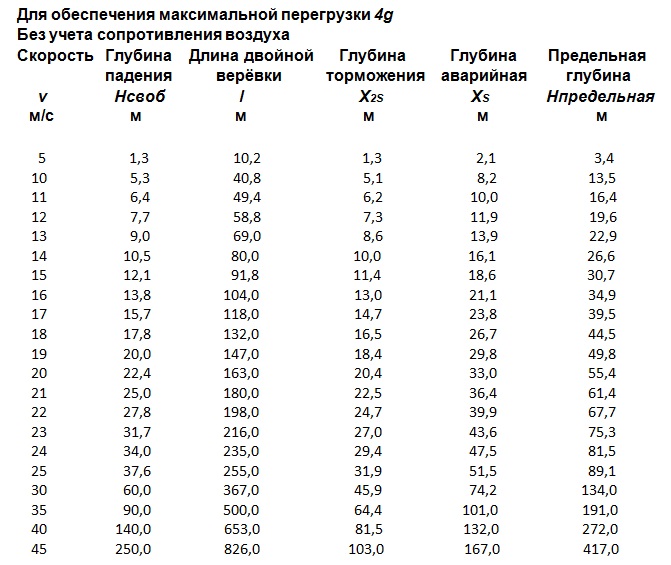
Определение глубины падения для объекта при линейной системе

Чтобы определить, с какой высоты должен быть выполнен прыжок для получения определённой глубины падения, надо сложить желаемую глубину падения с предельной глубиной торможения (на случай обрыва одной из веревок) и умножить эту сумму на технический коэффициент запаса (Kзап = от 1,2 до 1,33):

Пример: для глубины падения Hсвоб = 12,1 метра получаем искомую высоту объекта:

Hобъекта = Hпредельная * Kзап.

Hобъекта = 30,7 * 1,2 = 36,8 метров, и длину двойной верёвки торможения надо использовать не менее 91,8 метров.

Такой расчет выполняют реже, лишь для достижения спортивных целей. Скажем, подобрать объект, чтобы совершить акробатический трюк.

Самой важной задачей представляется другая. Определить на имеющемся объекте максимальную безопасную глубину падения и количество тормозящей верёвки.

Итак, измерив высоту объекта, находим

Hпредельная = Hобъекта / Kзап.

А затем получаем подбором по таблице:

Hсвоб и l двойная.

Пример: для объекта высотой Hобъекта = 38 метров и Kзап = 1,2 имеем:

Hпредельная = 38 / 1,2 = 31,7 метра. По таблице определяем ближайшее меньшее Hпредельная = 30,7 метра, а также для неё глубину падения Hсвоб = 12,1 метра и количество двойной динамической верёвки l двойная = 91,8 метров.

Перпендикулярная амортизация

Расчётные данные для стандартных динамических верёвок показывают значительную длину амортизирующей верёвки, которая обеспечивает безопасную глубину торможения.

Предлагается расположить фрагмент растяжения в перпендикулярном направлении и использовать свойство V-образного разложения сил.

Желаемое свойство состоит в следующем. Нагрузка на плечи V-образного натяжения при угле между плечами более 120 градусов всегда больше силы оттяжки. Таким образом, амортизирующее растяжение располагают по V-плечам, сохраняя направление перемещения соединения, в процессе торможения, перпендикулярно линии крепления плеч.

.

Это позволяет наиболее эффективно получить максимальное поглощение энергии при торможении за счет перемещения центрального узла плеч на начальном этапе амортизации.

Важным геометрическим свойством V-систем является тот факт, что приращению (деформации) длины плеч 2*Δl соответствует более значительное перемещение точки соединения плеч. Длиннее траектория в диапазоне изменения силы при деформации.

Рассмотрим предельный для использования в амортизации угол между плечами V-системы равный 120 градусам. Это наиболее просто увидеть, воспользовавшись тригонометрическими пропорциями в прямоугольном треугольнике с углом 60 градусов.

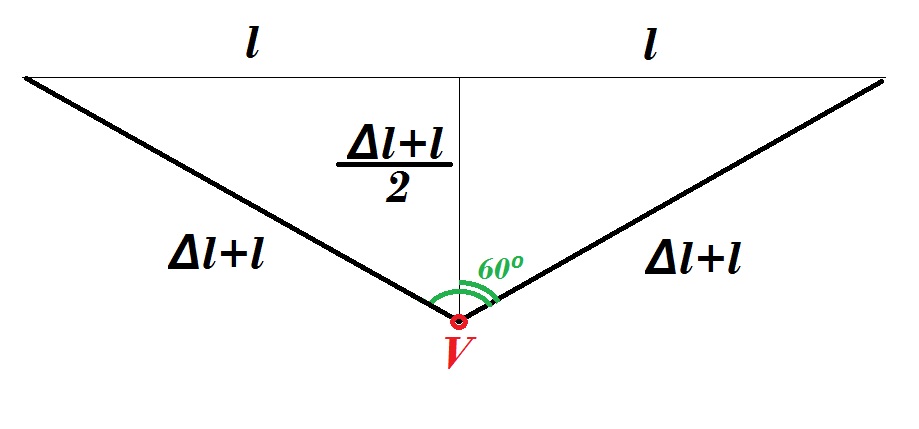
Тогда относительное удлинение каждого плеча равно (Δl / l) = 1 / (sin (120⁰/2)) – 1 = 0,155.

Суммарное относительное удлинение V-системы составит: 2 * (Δl / l) = 2*0,155 = 0,31.

А относительное перемещение точки V-плеч равно: cos (120⁰/2) = 0,5.

Таким образом, даже предельное для использования перемещение соединения V-плеч преодолевает расстояние в 0,5 / 0,31 = 1,61 раза больше, чем сама деформация верёвки.

Ниже представлена таблица преимущества перемещения точки соединения V-плеч для непредельных углов перпендикулярной амортизации:

Описание комбинированной системы

В соответствии со свойствами соединения упругих систем, их последовательное соединение увеличивает мягкость системы, а параллельное увеличивает жесткость.

Размещаем последовательно две системы для комбинации их свойств в направлении возрастания мягкости. Первая система представляет собой V-образную амортизацию натянутой верёвкой (одинарной или двойной – по принципу дублирования), закреплённой на противоположных концах. Вторая – это линейная амортизация верёвкой (также, одинарной или двойной), которая закреплена одним концом в середине V-образной, а второй свободный конец подсоединён к прыгуну.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.