 полная версия
полная версияSix Lectures on Light. Delivered In The United States In 1872-1873
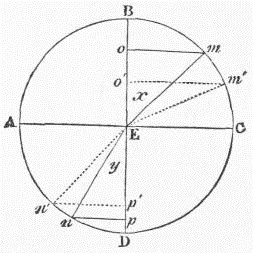
Fig. 5
In all cases where the light is incident from air upon the surface of a solid or a liquid, or, to speak more generally, when the incidence is from a less highly refracting to a more highly refracting medium, the reflection is partial. In this case the most powerfully reflecting substances either transmit or absorb a portion of the incident light. At a perpendicular incidence water reflects only 18 rays out of every 1,000; glass reflects only 25 rays, while mercury reflects 666 When the rays strike the surface obliquely the reflection is augmented. At an incidence of 40°, for example, water reflects 22 rays, at 60° it reflects 65 rays, at 80° 333 rays; while at an incidence of 89½°, where the light almost grazes the surface, it reflects 721 rays out of every 1,000. Thus, as the obliquity increases, the reflection from water approaches, and finally quite overtakes, the perpendicular reflection from mercury; but at no incidence, however great, when the incidence is from air, is the reflection from water, mercury, or any other substance, total.
Still, total reflection may occur, and with a view to understanding its subsequent application in the Nicol's prism, it is necessary to state when it occurs. This leads me to the enunciation of a principle which underlies all optical phenomena—the principle of reversibility.5 In the case of refraction, for instance, when the ray passes obliquely from air into water, it is bent towards the perpendicular; when it passes from water to air, it is bent from the perpendicular, and accurately reverses its course. Thus in fig. 5, if m E n be the track of a ray in passing from air into water, n E m will be its track in passing from water into air. Let us push this principle to its consequences. Supposing the light, instead of being incident along m E or m′ E, were incident as close as possible along C E (fig. 6); suppose, in other words, that it just grazes the surface before entering the water. After refraction it will pursue say the course E n″. Conversely, if the light start from n″, and be incident at E, it will, on escaping into the air, just graze the surface of the water. The question now arises, what will occur supposing the ray from the water to follow the course n‴ E, which lies beyond n″ E? The answer is, it will not quit the water at all, but will be totally reflected (along E x). At the under surface of the water, moreover, the law is just the same as at its upper surface, the angle of incidence (D E n‴) being equal to the angle of reflection (D E x).
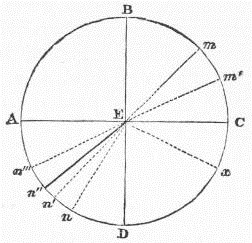
Fig. 6
Total reflection may be thus simply illustrated:—Place a shilling in a drinking-glass, and tilt the glass so that the light from the shilling shall fall with the necessary obliquity upon the water surface above it. Look upwards through the water towards that surface, and you see the image of the shilling shining there as brightly as the shilling itself. Thrust the closed end of an empty test-tube into water, and incline the tube. When the inclination is sufficient, horizontal light falling upon the tube cannot enter the air within it, but is totally reflected upward: when looked down upon, such a tube looks quite as bright as burnished silver. Pour a little water into the tube; as the liquid rises, total reflection is abolished, and with it the lustre, leaving a gradually diminishing shining zone, which disappears wholly when the level of the water within the tube reaches that without it. Any glass tube, with its end stopped water-tight, will produce this effect, which is both beautiful and instructive.
Total reflection never occurs except in the attempted passage of a ray from a more refracting to a less refracting medium; but in this case, when the obliquity is sufficient, it always occurs. The mirage of the desert, and other phantasmal appearances in the atmosphere, are in part due to it. When, for example, the sun heats an expanse of sand, the layer of air in contact with the sand becomes lighter and less refracting than the air above it: consequently, the rays from a distant object, striking very obliquely on the surface of the heated stratum, are sometimes totally reflected upwards, thus producing images similar to those produced by water. I have seen the image of a rock called Mont Tombeline distinctly reflected from the heated air of the strand of Normandy near Avranches; and by such delusive appearances the thirsty soldiers of the French army in Egypt were greatly tantalised.
The angle which marks the limit beyond which total reflection takes place is called the limiting angle (it is marked in fig. 6 by the strong line E n″). It must evidently diminish as the refractive index increases. For water it is 48½°, for flint glass 38°41', and for diamond 23°42'. Thus all the light incident from two complete quadrants, or 180°, in the case of diamond, is condensed into an angular space of 47°22' (twice 23°42') by refraction. Coupled with its great refraction, are the great dispersive and great reflective powers of diamond; hence the extraordinary radiance of the gem, both as regards white light and prismatic light.
§ 5. Velocity of Light. Aberration. Principle of least Action
In 1676 a great impulse was given to optics by astronomy. In that year Olav Roemer, a learned Dane, was engaged at the Observatory of Paris in observing the eclipses of Jupiter's moons. The planet, whose distance from the sun is 475,693,000 miles, has four satellites. We are now only concerned with the one nearest to the planet. Roemer watched this moon, saw it move round the planet, plunge into Jupiter's shadow, behaving like a lamp suddenly extinguished: then at the other edge of the shadow he saw it reappear, like a lamp suddenly lighted. The moon thus acted the part of a signal light to the astronomer, and enabled him to tell exactly its time of revolution. The period between two successive lightings up of the lunar lamp he found to be 42 hours, 28 minutes, and 35 seconds.
This measurement of time was so accurate, that having determined the moment when the moon emerged from the shadow, the moment of its hundredth appearance could also be determined. In fact, it would be 100 times 42 hours, 28 minutes, 35 seconds, after the first observation.
Roemer's first observation was made when the earth was in the part of its orbit nearest Jupiter. About six months afterwards, the earth being then at the opposite side of its orbit, when the little moon ought to have made its hundredth appearance, it was found unpunctual, being fully 15 minutes behind its calculated time. Its appearance, moreover, had been growing gradually later, as the earth retreated towards the part of its orbit most distant from Jupiter. Roemer reasoned thus: 'Had I been able to remain at the other side of the earth's orbit, the moon might have appeared always at the proper instant; an observer placed there would probably have seen the moon 15 minutes ago, the retardation in my case being due to the fact that the light requires 15 minutes to travel from the place where my first observation was made to my present position.'
This flash of genius was immediately succeeded by another. 'If this surmise be correct,' Roemer reasoned, 'then as I approach Jupiter along the other side of the earth's orbit, the retardation ought to become gradually less, and when I reach the place of my first observation, there ought to be no retardation at all.' He found this to be the case, and thus not only proved that light required time to pass through space, but also determined its rate of propagation.
The velocity of light, as determined by Roemer, is 192,500 miles in a second.
For a time, however, the observations and reasonings of Roemer failed to produce conviction. They were doubted by Cassini, Fontenelle, and Hooke. Subsequently came the unexpected corroboration of Roemer by the English astronomer, Bradley, who noticed that the fixed stars did not really appear to be fixed, but that they describe little orbits in the heavens every year. The result perplexed him, but Bradley had a mind open to suggestion, and capable of seeing, in the smallest fact, a picture of the largest. He was one day upon the Thames in a boat, and noticed that as long as his course remained unchanged, the vane upon his masthead showed the wind to be blowing constantly in the same direction, but that the wind appeared to vary with every change in the direction of his boat. 'Here,' as Whewell says, 'was the image of his case. The boat was the earth, moving in its orbit, and the wind was the light of a star.'
We may ask, in passing, what, without the faculty which formed the 'image,' would Bradley's wind and vane have been to him? A wind and vane, and nothing more. You will immediately understand the meaning of Bradley's discovery. Imagine yourself in a motionless railway-train, with a shower of rain descending vertically downwards. The moment the train begins to move, the rain-drops begin to slant, and the quicker the motion of the train the greater is the obliquity. In a precisely similar manner the rays from a star, vertically overhead, are caused to slant by the motion of the earth through space. Knowing the speed of the train, and the obliquity of the falling rain, the velocity of the drops may be calculated; and knowing the speed of the earth in her orbit, and the obliquity of the rays due to this cause, we can calculate just as easily the velocity of light. Bradley did this, and the 'aberration of light,' as his discovery is called, enabled him to assign to it a velocity almost identical with that deduced by Roemer from a totally different method of observation. Subsequently Fizeau, and quite recently Cornu, employing not planetary or stellar distances, but simply the breadth of the city of Paris, determined the velocity of light: while Foucault—a man of the rarest mechanical genius—solved the problem without quitting his private room. Owing to an error in the determination of the earth's distance from the sun, the velocity assigned to light by both Roemer and Bradley is too great. With a close approximation to accuracy it may be regarded as 186,000 miles a second.
By Roemer's discovery, the notion entertained by Descartes, and espoused by Hooke, that light is propagated instantly through space, was overthrown. But the establishment of its motion through stellar space led to speculations regarding its velocity in transparent terrestrial substances. The 'index of refraction' of a ray passing from air into water is 4/3. Newton assumed these numbers to mean that the velocity of light in water being 4, its velocity in air is 3; and he deduced the phenomena of refraction from this assumption. Huyghens took the opposite and truer view. According to this great man, the velocity of light in water being 3, its velocity in air is 4; but both in Newton's time and ours the same great principle determined, and determines, the course of light in all cases. In passing from point to point, whatever be the media in its path, or however it may be refracted or reflected, light takes the course which occupies least time. Thus in fig. 4, taking its velocity in air and in water into account, the light reaches G from I more rapidly by travelling first to O, and there changing its course, than if it proceeded straight from I to G. This is readily comprehended, because, in the latter case, it would pursue a greater distance through the water, which is the more retarding medium.
§ 6. Descartes' Explanation of the Rainbow
Snell's law of refraction is one of the corner-stones of optical science, and its applications to-day are million-fold. Immediately after its discovery Descartes applied it to the explanation of the rainbow. A beam of solar light falling obliquely upon a rain-drop is refracted on entering the drop. It is in part reflected at the back of the drop, and on emerging it is again refracted. By these two refractions, and this single reflection, the light is sent to the eye of an observer facing the drop, and with his back to the sun.
Conceive a line drawn from the sun, through the back of his head, to the observer's eye and prolonged beyond it. Conceive a second line drawn from the shower to the eye, and enclosing an angle of 42½° with the line drawn from the sun. Along this second line a rain-drop when struck by a sunbeam will send red light to the eye. Every other drop similarly situated, that is, every drop at an angular distance of 42½° from the line through the sun and eye, will do the same. A circular band of red light is thus formed, which may be regarded as the boundary of the base of a cone, with its apex at the observer's eye. Because of the magnitude of the sun, the angular width of this red band will be half a degree.
From the eye of the observer conceive another line to be drawn, enclosing an angle, not of 42½°, but of 40½°, with the prolongation of the line drawn from the sun. Along this other line a rain-drop, at its remote end, when struck by a solar beam, will send violet light to the eye. All drops at the same angular distance will do the same, and we shall therefore obtain a band of violet light of the same width as the red band. These two bands constitute the limiting colours of the rainbow, and between them the bands corresponding to the other colours lie.
Thus the line drawn from the eye to the middle of the bow, and the line drawn through the eye to the sun, always enclose an angle of about 41°. To account for this was the great difficulty, which remained unsolved up to the time of Descartes.
Taking a pen in hand, and calculating by means of Snell's law the track of every ray through a raindrop, Descartes found that, at one particular angle, the rays, reflected at its back, emerged from the drop almost parallel to each other. They were thus enabled to preserve their intensity through long atmospheric distances. At all other angles the rays quitted the drop divergent, and through this divergence became so enfeebled as to be practically lost to the eye. The angle of parallelism here referred to was that of forty-one degrees, which observation had proved to be invariably associated with the rainbow.
From what has been said, it is clear that two observers standing beside each other, or one above the other, nay, that even the two eyes of the same observer, do not see exactly the same bow. The position of the base of the cone changes with that of its apex. And here we have no difficulty in answering a question often asked—namely, whether a rainbow is ever seen reflected in water. Seeing two bows, the one in the heavens, the other in the water, you might be disposed to infer that the one bears the same relation to the other that a tree upon the water's edge bears to its reflected image. The rays, however, which reach an observer's eye after reflection from the water, and which form a bow in the water, would, were their course from the shower uninterrupted, converge to a point vertically under the observer, and as far below the level of the water as his eye is above it. But under no circumstances could an eye above the water-level and one below it see the same bow—in other words, the self-same drops of rain cannot form the reflected bow and the bow seen directly in the heavens. The reflected bow, therefore, is not, in the usual optical sense of the term, the image of the bow seen in the sky.
§ 7. Analysis and Synthesis of Light. Doctrine of Colours
In the rainbow a new phenomenon was introduced—the phenomenon of colour. And here we arrive at one of those points in the history of science, when great men's labours so intermingle that it is difficult to assign to each worker his precise meed of honour. Descartes was at the threshold of the discovery of the composition of solar light; but for Newton was reserved the enunciation of the true law. He went to work in this way: Through the closed window-shutter of a room he pierced an orifice, and allowed a thin sunbeam to pass through it. The beam stamped a round white image of the sun on the opposite wall of the room. In the path of this beam Newton placed a prism, expecting to see the beam refracted, but also expecting to see the image of the sun, after refraction, still round. To his astonishment, it was drawn out to an image with a length five times its breadth. It was, moreover, no longer white, but divided into bands of different colours. Newton saw immediately that solar light was composite, not simple. His elongated image revealed to him the fact that some constituents of the light were more deflected by the prism than others, and he concluded, therefore, that white light was a mixture of lights of different colours, possessing different degrees of refrangibility.
Let us reproduce this celebrated experiment. On the screen is now stamped a luminous disk, which may stand for Newton's image of the sun. Causing the beam (from the aperture L, fig. 7) which produces the disk to pass through a lens (E), we form a sharp image of the aperture. Placing in the track of the beam a prism (P), we obtain Newton's coloured image, with its red and violet ends, which he called a spectrum. Newton divided the spectrum into seven parts—red, orange, yellow, green, blue, indigo, violet; which are commonly called the seven primary or prismatic colours. The drawing out of the white light into its constituent colours is called dispersion.
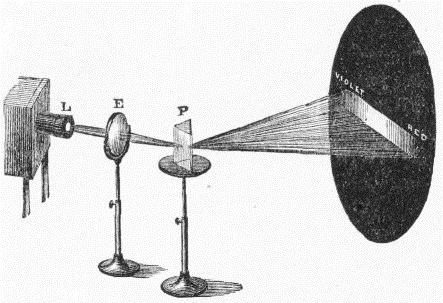
Fig. 7.
This was the first analysis of solar light by Newton; but the scientific mind is fond of verification, and never neglects it where it is possible. Newton completed his proof by synthesis in this way: The spectrum now before you is produced by a glass prism. Causing the decomposed beam to pass through a second similar prism, but so placed that the colours are refracted back and reblended, the perfectly white luminous disk is restored.
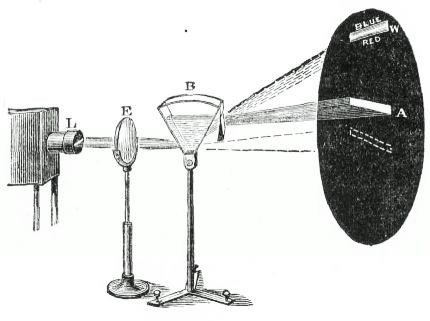
Fig. 8.
In this case, refraction and dispersion are simultaneously abolished. Are they always so? Can we have the one without the other? It was Newton's conclusion that we could not. Here he erred, and his error, which he maintained to the end of his life, retarded the progress of optical discovery. Dollond subsequently proved that by combining two different kinds of glass, the colours can be extinguished, still leaving a residue of refraction, and he employed this residue in the construction of achromatic lenses—lenses yielding no colour—which Newton thought an impossibility. By setting a water-prism—water contained in a wedge-shaped vessel with glass sides (B, fig. 8)—in opposition to a wedge of glass (to the right of B), this point can be illustrated before you. We have first of all the position (dotted) of the unrefracted beam marked upon the screen; then we produce the narrow water-spectrum (W); finally, by introducing a flint-glass prism, we refract the beam back, until the colour disappears (at A). The image of the slit is now white; but though the dispersion is abolished, there remains a very sensible amount of refraction.
This is the place to illustrate another point bearing upon the instrumental means employed in these lectures. Bodies differ widely from each other as to their powers of refraction and dispersion. Note the position of the water-spectrum upon the screen. Altering in no particular the wedge-shaped vessel, but simply substituting for the water the transparent bisulphide of carbon, you notice how much higher the beam is thrown, and how much richer is the display of colour. To augment the size of our spectrum we here employ (at L) a slit, instead of a circular aperture.6
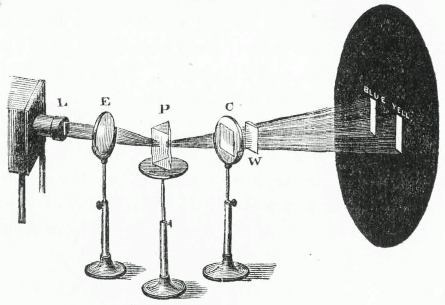
Fig. 9.
The synthesis of white light may be effected in three ways, all of which are worthy of attention: Here, in the first instance, we have a rich spectrum produced by the decomposition of the beam (from L, fig. 9). One face of the prism (P) is protected by a diaphragm (not shown in the figure), with a longitudinal slit, through which the beam passes into the prism. It emerges decomposed at the other side. I permit the colours to pass through a cylindrical lens (C), which so squeezes them together as to produce upon the screen a sharply defined rectangular image of the longitudinal slit. In that image the colours are reblended, and it is perfectly white. Between the prism and the cylindrical lens may be seen the colours, tracking themselves through the dust of the room. Cutting off the more refrangible fringe by a card, the rectangle is seen red: cutting off the less refrangible fringe, the rectangle is seen blue. By means of a thin glass prism (W), I deflect one portion of the colours, and leave the residual portion. On the screen are now two coloured rectangles produced in this way. These are complementary colours—colours which, by their union, produce white. Note, that by judicious management, one of these colours is rendered yellow, and the other blue. I withdraw the thin prism; yellow and blue immediately commingle, and we have white as the result of their union. On our way, then, we remove the fallacy, first exposed by Wünsch, and afterwards independently by Helmholtz, that the mixture of blue and yellow lights produces green.
Restoring the circular aperture, we obtain once more a spectrum like that of Newton. By means of a lens, we can gather up these colours, and build them together, not to an image of the aperture, but to an image of the carbon-points themselves.
Finally, by means of a rotating disk, on which are spread in sectors the colours of the spectrum, we blend together the prismatic colours in the eye itself, and thus produce the impression of whiteness.
Having unravelled the interwoven constituents of white light, we have next to inquire, What part the constitution so revealed enables this agent to play in Nature? To it we owe all the phenomena of colour, and yet not to it alone; for there must be a certain relationship between the ultimate particles of natural bodies and white light, to enable them to extract from it the luxury of colour. But the function of natural bodies is here selective, not creative. There is no colour generated by any natural body whatever. Natural bodies have showered upon them, in the white light of the sun, the sum total of all possible colours; and their action is limited to the sifting of that total—the appropriating or absorbing of some of its constituents, and the rejecting of others. It will fix this subject in your minds if I say, that it is the portion of light which they reject, and not that which they appropriate or absorb, that gives bodies their colours.
Let us begin our experimental inquiries here by asking, What is the meaning of blackness? Pass a black ribbon through the colours of the spectrum; it quenches all of them. The meaning of blackness is thus revealed—it is the result of the absorption of all the constituents of solar light. Pass a red ribbon through the spectrum. In the red light the ribbon is a vivid red. Why? Because the light that enters the ribbon is not quenched or absorbed, but in great part sent back to the eye. Place the same ribbon in the green of the spectrum; it is black as jet. It absorbs the green light, and renders the space on which that light falls a space of intense darkness. Place a green ribbon in the green of the spectrum. It shines vividly with its proper colour; transfer it to the red, it is black as jet. Here it absorbs all the light that falls upon it, and offers mere darkness to the eye.
Thus, when white light is employed, the red sifts it by quenching the green, and the green sifts it by quenching the red, both exhibiting the residual colour. The process through which natural bodies acquire their colours is therefore a negative one. The colours are produced by subtraction, not by addition. This red glass is red because it destroys all the more refrangible rays of the spectrum. This blue liquid is blue because it destroys all the less refrangible rays. Both together are opaque because the light transmitted by the one is quenched by the other. In this way, by the union of two transparent substances, we obtain a combination as dark as pitch to solar light. This other liquid, finally, is purple because it destroys the green and the yellow, and allows the terminal colours of the spectrum to pass unimpeded. From the blending of the blue and the red this gorgeous purple is produced.



