The Fontana History of Chemistry

Like Darwin’s Origin of Species, Lavoisier’s Traité was a hastily written abstract or prolegomena to a much larger work he intended to write that would have included a discussion of affinity, and animal and vegetable chemistry. Like Darwin’s book, it was all the more readable and influential for being short and introductory. If more information was required, Fourcroy’s encyclopedic text and its many English and German imitations soon provided reference and instruction. But this was not the end of the chemical revolution. To complete it, Lavoisier’s elements had to be reunited with the older corpuscular traditions of Boyle and Newton. This was to be the contribution of John Dalton.

4 A New System of Chemical Philosophy

Atoms are round bits of wood invented by Mr Dalton.

(H. E. ROSCOE, 1887)

Before Dalton came on the scene, chemistry can hardly be described as an exact science. A wealth of empirical facts had been established and many theories had been erected that bound them together, not the least impressive of which were Lavoisier’s new dualistic views of chemical composition and his explanations of combustion and acidity. Most of eighteenth-century chemical activity had been qualitative. Despite the Newtonian dream of quantifying the forces of attraction between chemical substances and the compilation of elaborate tables of chemical affinity, no powerful quantitative generalizations had emerged. Although these empirically derived affinity relations often allowed the course of a particular chemical reaction to be predicted, it was not possible to say, or to calculate, how much of each ingredient was needed to perform a reaction successfully and most economically. Dalton’s chemical atomic theory, and the laws of chemical combination that were explained by it, were to make such calculations and estimates possible – to the benefit of efficient analysis, synthesis and chemical manufacture.

As a consequence of the power of the corpuscular philosophy, by the end of the seventeenth century it had become a regulative principle, or self-evident truth, that all matter was ultimately composed of microscopic ‘solid, hard, impenetrable, moveable’ particles. As we saw in the second chapter, however, such ultimate descriptions of Nature were of little use to practical chemists, who preferred to adopt a number of empirically derived elementary substances as the basic ‘stuffs’ of chemical investigation. Lavoisier’s famous definition of the element in 1789 made it clear that speculations concerning the ultimate particles or atoms of matter were a waste of time; chemistry was to be based on experimental knowledge1:

All that can be said upon the number and nature of elements [i.e. in an Aristotelian or Paracelsian sense] is, in my opinion, confined to discussions entirely of a metaphysical nature. It is an unsolvable problem capable of an infinity of solutions none of which probably accord with Nature. I shall be content, therefore, in saying that if by the term elements we mean to express those simple and indivisible atoms of which matter is composed, it seems extremely probable we know nothing at all about them; however, if instead we apply the term elements or principles of bodies, to express our idea of the last point which analysis is capable of reaching, we must admit as elements, all the substances into which we are capable, by any means, to reduce bodies during decomposition. Not that we can be certain that these substances we consider as simple may not be compounded of two, or even a greater number of principles; but, since these principles cannot be separated, or rather since we have not hitherto discovered the means of separating them, they act with regard to us as simple substances, and we ought never to suppose them compounded until experiment and observation has proved them to be so.

For the same reason, although Dalton believed in physical atoms, most of his interpreters were content with a theory of chemical atoms – the ‘minima’ of the experimentally defined elements. Whether these chemical atoms were themselves composed from homogeneous or heterogeneous physical atoms was to go beyond the evidence of pure stoichiometry.

Stoichiometry was a subject invented by the German chemist Jeremias Richter (1762–1807), who had studied mathematics with the great philosopher, Immanuel Kant, at the University of Königsberg, and for whom he wrote a doctoral thesis on the use of mathematics in chemistry. This was, in practice, nothing grander than an account of the determination of specific gravities, from which Richter calculated the supposed weights of phlogiston in substances. Just as Kepler had searched for mathematical relations and harmony in astronomical data gathered by Tycho Brahe, so Richter spent his spare time as a chemical analyst in the Berlin porcelain works searching for arithmetical relations in chemistry. As Partington noted sardonically, Richter spent his entire life finding ‘regularities among the combining proportions where nature had not provided any’.

The exception was his discovery in 1792, while investigating double decompositions, that, because neutral products were formed, the reactants must ‘have amongst themselves a certain fixed ratio of mass’.

If, e.g., the components of two neutral compounds are A – a, a and B – b, b, then the mass ratios of the new neutral compounds produced by double decomposition are unchangeably A – a:b and B – b:a.

This law of neutrality was a special case of what came to be known as the law of reciprocal proportions. Richter referred to the study of these ratios as ‘stoichiometry’ and went on to examine how a fixed weight of an acid was neutralized by different weights of various bases. This investigation led him to claim, erroneously, that combining proportions formed arithmetical and geometrical series. It was Ernst Fischer, a Berlin physicist, who, when translating Berthollet’s Recherches sur la lois de l’affinité into German in 1802, pointed out that Richter’s results could be tabulated to show equivalent weights of a series of acids and bases. If 1000 parts of sulphuric acid was taken as a standard and the base equivalents needed for neutralization arranged in one column, and the amounts of other acids needed to neutralize these bases in another, then an analyst could gather at a glance how much of a particular base would neutralize a particular acid:

Thus, 672 equivalents of ammonia neutralized 427 of fluoric, 577 of carbonic and 712 of muriatic acids. Analysts now had a definite method of controlling the accuracy of their work and of calculating beforehand the composition of salts under investigation.

Dalton’s atomic theory was to provide a rational explanation for these regularities. There has been some debate as to whether Dalton was directly influenced by Richter. He certainly knew of Richter’s investigations, but probably not until after he had derived his own explanation from other sources.

DALTON’S ‘NEW SYSTEM’

What was ‘new’ in John Dalton’s A New System of Chemical Philosophy? The obvious reply seems to be the introduction of chemical atomism – the idea that each of Lavoisier’s undecompounded bodies was composed from a myriad of homogeneous atoms, each element’s atom differing slightly in mass. The surprising thing, however, is that only one chapter of barely five pages in the 916-page treatise was devoted to the epoch-making theme. These five pages, together with four explanatory plates, appeared at the end of the first part of the New System, which was published in Manchester in 1808 and dedicated to the professors and students of the Universities of Edinburgh and Glasgow, who had heard Dalton lecture on ‘Heat and the Chemical Elements’ in 1807, and to the members of Manchester’s Literary and Philosophical Society, who had ‘uniformly promoted’ Dalton’s researches. A second, continuously paginated, part of the New System, dedicated to Humphry Davy and William Henry, was published in 1810. Astonishingly, the third part, labelled as a second volume, did not appear until 1827. Even then the design was incomplete and a promised final part concerned with ‘complex compounds’ was never published.

Dalton’s apparent dilatoriness is easily explained by the fact that he earned his living as a private elementary teacher, which left him little time for the exacting experimental work and evidence upon which he based the New System. For it was a ‘new’ approach that he was taking, familiar though his scheme has become. Dalton recognized his innovation as being a ‘doctrine of heat and general principles of chemical synthesis’. A theory of mixed gases, which he developed in 1802, led him in 1803 to ‘new views’ on heat as a factor in the way elements (or, rather, atoms) combined together, a process he referred to as ‘chemical synthesis’. The fact that chemical compounds, or compound atoms (molecules), might be binary, ternary, quaternary, and so on up to a maximum of twelve atoms, gave Dalton a structure for his text: a detailed experimental examination of heat and the gaseous state, a theory of atomism and combination, which included the measure of atomic mass as a relative atomic weight, followed by a detailed account of the properties of the known elements, their binary combinations, ternary combinations and so on. Thus, although the exegesis of the atomic theory was limited to five pages, the whole of the New System was, in fact, imbued with a new stoichiometric approach to chemistry – that elements compounded together in fixed proportions by weight because of attractions and repulsions between the tiny particles of heat and elementary forms that made up laboratory chemicals. Inevitably, because Dalton was a slow worker and unable to spare time from teaching for research and writing, it was left largely to others, notably Thomas Thomson and Jacob Berzelius, to exploit the full consequences of Dalton’s insight.

DALTON’S LIFE

John Dalton (1766–1844) was born at Eaglesfield in Cumbria, the son of a weaver, and, like most contemporary members of the Society of Friends, was a man of some learning. The highly efficient Quaker network of schooling and informal education ensured that Dalton received a good schooling; he himself began to teach village schoolchildren when he reached the age of twelve. In his teens he mastered sufficient geometry to be able to study Newton’s Principia. At the age of fifteen, Dalton and his brother moved to Kendall, in the English Lake District, where they acquired their own school, which offered Greek, Latin, French and mathematics. At Kendall, Dalton was befriended by the blind Quaker scholar, John Gough, who further encouraged Dalton’s mathematical abilities and knowledge of Newtonian natural philosophy, including the work of Boyle and Boerhaave. The constant stimulation of rapidly changing weather conditions among the mountains and lakes of Westmorland and Cumberland (present-day Cumbria) interested him in meteorology. The records he kept over a five-year period were published in Meteorological Essays in 1793. In the same year, on Gough’s recommendation, Dalton moved to Manchester as tutor in mathematics and natural philosophy at New College, a Dissenting academy that had begun its distinguished life elsewhere as the Warrington Academy. Here Priestley had taught between 1761 and 1767.

Although Manchester New College moved to York in 1803, Dalton, finding Manchester congenial, spent the remainder of his life there as a private teacher and industrial consultant. Not only was there an abundance of paid work in Manchester for private tutors because of a rising industrial middle class (Dalton’s most famous pupil was a brewer’s son, the physicist James Prescott Joule), but the presence of the Literary and Philosophical Society, whose Secretary Dalton became in 1800 and President from 1817 until his death, proved a congenial venue for the presentation and articulation of his scientific work. Dalton read his first scientific paper, on self-diagnosed colour blindness (long after known as Daltonism) to the Society in 1794. He went on reading papers and reports to the Society up to his death. From about 1815 onwards, however, Dalton failed more and more to keep pace with the chemical literature. In 1839 he suffered the ignominy of having a paper of his on phosphates and arsenates rejected by the Royal Society on the grounds that a superior account of these salts had already been published by Thomas Graham.

Despite such failings, Dalton retained the respect of the chemical and scientific communities. Together with two other Dissenters from Anglicanism, Michael Faraday and Robert Brown, the botanist, and despite the angry opposition of Oxford High Churchmen, Dalton was awarded an honorary degree by Oxford University in 1832. A year later the government awarded him a Civil List pension for life, and in 1834 Edinburgh University gave him another honorary degree. His final accolade was a public funeral in Manchester. Even if we grant that some of these honours served a secondary purpose of drawing attention to scientists and their contribution to culture in Victorian Britain, we are bound to ask: What did Dalton do to merit such public honours?

THE ATOMIC THEORY

The straightforward answer is that Dalton rendered intelligible the many hundreds of quantitative analyses of substances that were recorded in the chemical literature and that he provided a model for the long-standing assumption made by chemists that compounds were formed from the combination of constant amounts of their constituents. He regarded chemical reactions as the reshuffling of atoms into new clusters (or molecules), these atoms and compound atoms being pictured in a homely way as little solid balls surrounded by a variable atmosphere of heat.

This statement, however, tells us little about Dalton’s originality; after all, the atomic theory of matter had existed for a good two-thousand years before Dalton’s birth. In Ireland, at the end of the eighteenth century, William Higgins (1762–1825) had used atomism in his A Comparative View of the Phlogiston and Antiphlogiston Theories (1789) to refute the phlogistic views of his countryman, Richard Kirwan. Higgins later claimed that Dalton had stolen his ideas – an inherently implausible notion that, nevertheless, has been supported by several historians in the past. In fact, Dalton’s originality lay in solving the problem of what philosophers of science have called transduction; he derived a way of calculating the relative weights of the ultimate particles of matter from observations and measurements that were feasible in the laboratory. Although atomic particles could never be individually weighed or seen or touched, Dalton provided a ‘calculus of chemical measurement’ that for the first time in history married the theory of atoms with tangible reality. He had transduced what had hitherto been a theoretical entity by building a bridge between experimental data and hypothetical atoms.

Dalton’s calculus involved four basic, but reasonable, assumptions. First, it was supposed that all matter was composed of solid and indivisible atoms. Unlike Newton’s and Priestley’s particles, Dalton’s atoms contained no inner spaces. They were completely incompressible. On the other hand, recognizing the plausibility of Lavoisier’s caloric model of changes of phase, Dalton supposed that atoms were surrounded by an atmosphere of heat, the quantity of which differed according to the solid, liquid or gaseous phase of the aggregate of atoms. A gas, for example, possessed a larger atmosphere of heat than the same matter in the solid state. Secondly, Dalton assumed, as generations of analysts before him had done, that substances (and hence their atoms) were indestructible and preserved their identities in all chemical reactions. If this law of conservation of mass and of the elements was not assumed, of course, transmutation would be possible and chemists would return to the dark days of alchemy. Thirdly, in view of Lavoisier’s operational definition of elements, Dalton assumed that there were as many different kinds of atoms as there were elements. Unlike Boyle and Newton, for Dalton there was not one primary, homogeneous ‘stuff’; rather, particles of hydrogen differed from particles of oxygen and all the particles that had so far been defined as elementary.

In these three assumptions Dalton moved away completely from the tradition of eighteenth-century matter theory, which had emphasized the identity of matter and of all material substances. In so doing. Dalton intimately bound his kind of atomism to the question of how elements were to be defined. In a final assumption, he proposed to do something that neither Lavoisier nor Higgins had thought of doing, namely to rid metaphysical atomism of its intangibleness by fixing a determinable property to it, that of relative atomic weight. To perform this transductive trick, Dalton had to make a number of simple assumptions about how atoms would combine to form compound atoms, the process he termed chemical synthesis. In the simplest possible case, ‘when only one combination of two bodies can be obtained, it must be presumed to be a binary one, unless some cause appear to the contrary’. In other words, although substances A and B might combine to form A2B2, it is simpler to assume that they will usually form just AB. Similarly, if ‘two combinations are observed, they must be presumed to be a binary and a ternary’:

A + 2B = AB2 or 2A + B = A2B

Dalton made similar rules for cases of three and four compounds of the same elements, and pointed out that the rules of synthesis also applied to the combination of compounds:

CD + DE = CD2E etc.

These assumptions of simplicity of composition, which, as we shall see, had a theoretical justification, have long since been replaced by different criteria. Although they led to many erroneous results, the assumptions proved fruitful since they allowed relative atomic weights to be calculated. Two examples, both given by Dalton, will suffice.

Hydrogen and oxygen were known to form water. Before 1815, when hydrogen peroxide was discovered, this was the only known compound of these two gases. Dalton quite properly assumed, therefore, that they formed a binary compound; in present-day symbols:

H + O = HO

From Humboldt and Gay-Lussac’s analyses of water, it was known that 87.4 parts by weight of oxygen combined with 12.6 parts of hydrogen to form water. This ratio, H : O :: 12.6 : 87.4, must also be the ratio of the individual weights of hydrogen and oxygen atoms that make up the binary atom of water. Since hydrogen is the lightest substance known, it made sense to’ adopt it as a standard and to compare all heavier chemical objects with it. If the hydrogen atom is defined as having a weight of 1, the relative atomic weight of an atom of oxygen will be roughly 7. (Dalton always rounded calculations up or down to the nearest whole number.) Similarly, Dalton assumed ammonia to be a binary compound of azote (nitrogen) and hydrogen. From Berthollet’s analysis he calculated the relative atomic weight of nitrogen to be 5 or, after further experiments in 1810, 6.

TABLE 4.1 Some of Dalton’s relative weights.

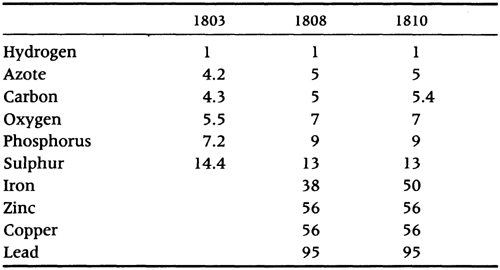
Dalton was well aware of the arbitrary nature of his rules of simplicity. In the second part of the New System in 1810 he allowed the possibility that water could be a ternary compound, in which case oxygen would be 14 times heavier than hydrogen; or, if two atoms of oxygen were combined with one of hydrogen, oxygen’s atomic weight would be 3.5. This uncertainty was to plague chemists for another fifty years.

From the beginning, Dalton symbolized his atoms2:

… by a small circle, with some distinctive mark; and the combinations consist in the juxta-position of two or more of these.

The synthesis of water and ammonia were represented as:

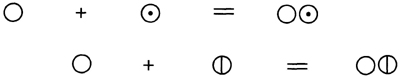
Such symbols referred to the atom and were therefore conceptually very different from alchemical symbols or those of Hassenfratz and Adet, which only had a hazy or qualitative meaning. Earlier symbols had been a shorthand; Dalton’s circles conveyed a theoretical meaning as well as being a convenient abbreviation.

Dalton was never to become reconciled to the symbols introduced by Berzelius, even though he himself used alphabetical abbreviations within circles for elements such as iron, sulphur, copper and lead. In 1837, soon after the British Association for the Advancement of Science had persuaded British chemists to adopt Berzelius’ symbols, Dalton wrote a testimonial for Thomas Graham’s application for the Chair of Chemistry at University College London.

Berzelius’s symbols are horrifying: a young student in chemistry might as soon learn Hebrew as make himself acquainted with them. They appear like a chaos of atoms. Why not put them together in some sort of order?…[They] equally perplex the adepts of science, discourage the learner, as well as to cloud the beauty and simplicity of the Atomic Theory.

Clearly Dalton felt strongly about his innovation and was prepared to criticize a professorial candidate with one hand while supporting him with another. Indeed, Dalton suffered the first of his two strokes in April 1837 after angrily discussing symbols with a visitor.

Dalton’s symbols did not survive, mainly one suspects because they were an additional printing expense, but both they, as well as Berzelius’ simplification, encouraged people to acquire a faith in the reality of chemical atoms and enabled chemists to visualize relatively complex chemical reactions. As in mathematics, chemistry could advance only to a certain degree without an adequate symbolism for its deeper study. Between them, Lavoisier and Dalton completed a revolution in the language of chemistry.

Dalton’s hieroglyphs also reveal that he had a three-dimensional geometrical model of combination in mind. When three or more particles combined, he conceived that like particles stationed themselves as far apart as possible. This conception offers not only an important clue concerning the origins of Dalton’s atomic theory, but an explanation of his opposition to the notion derived from the volumetric combination of gases that equal volumes contained equal numbers of particles.

THE ORIGINS OF DALTON’S THEORY

How did Dalton come to think of weighing atoms? There have been many different attempts by chemists and historians to explain this. Dalton supplied three, mutually inconsistent, accounts of his voyage of discovery. Reconstruction has been made difficult by the fact that most of Dalton’s surviving papers were destroyed during the Second World War, and, but for the fact that Henry Roscoe and Arthur Harden quoted from them in a historical study published in 1896, historians would have been hard-pressed for evidence. Although the debate over influences remains unresolved, all historians agree that Dalton must have come to his ‘new views’ through the study of the physical properties of gases, which in turn depended upon his youthful interest in meteorology. For, once air had been shown to be heterogeneous, and not a homogeneous element, the question arose whether oxygen, nitrogen, carbon dioxide and water vapour were chemically combined in air (perhaps a compound actually dissolved in the water vapour?) or merely mixed together. The fact that atmospheric air appeared to be homogeneous and that its gaseous components were not stratified according to their specific gravities (itself an indication that chemists like Priestley were prepared to think in terms of the specific weights of gas particles long before Dalton) made most late-eighteenth-century chemists believe that atmospheric gases were chemically combined.