The Number Mysteries: A Mathematical Odyssey through Everyday Life

Take a piece of wire and bend it into a square. Dip it in bubble mixture and blow. Why isn’t it a cube-shaped bubble that comes out the other side? Or if the wire is triangular, why can’t you blow a pyramid-shaped bubble? Why is it that, regardless of the shape of the frame, the bubble comes out as a perfect spherical ball? The answer is that nature is lazy, and the sphere is nature’s easiest shape. The bubble tries to find the shape that uses the least amount of energy, and that energy is proportional to the surface area. The bubble contains a fixed volume of air, and that volume does not change if the shape changes. The sphere is the shape that has the smallest surface area which can contain that fixed amount of air. That makes it the shape that uses the least amount of energy.

Manufacturers have long been keen to copy nature’s ability to make perfect spheres. If you’re making ball bearings or shot for guns, getting perfect spheres could be a matter of life and death, since a slight imperfection in the spherical shape could lead to a gun backfiring or a machine breaking down. The breakthrough came in 1783 when a Bristol-born plumber, William Watts, realized that he could exploit nature’s predilection for spheres.

When molten iron is dropped from the top of a tall tower, like the bubble the liquid droplets form into perfect spheres during their descent. Watts wondered whether, if you stuck a vat of water at the bottom of the tower, you could freeze the spherical shapes as the droplets of iron hit the water. He decided to try his idea out in his own house in Bristol. The trouble was that he needed the drop to be further than three floors to give the falling molten lead time to form into spherical droplets.

So Watts added another three storeys on top of his house and cut holes in all the floors to allow the lead to fall through the building. The neighbours were a bit shocked by the sudden appearance of this tower on the top of his home, despite his attempts to give it a Gothic twist with the addition of some castlelike trim around the top. But so successful were Watts’s experiments that similar towers soon shot up across England and America. His own shot tower stayed in operation until 1968.

Although nature uses the sphere so often, how can we be sure that there isn’t some other strange shape that might be even more efficient than the sphere? It was the great Greek mathematician Archimedes who first proposed that the sphere was indeed the shape with the smallest surface area containing a fixed volume. To try to prove this, Archimedes began by producing formulas for calculating the surface area of a sphere and volume enclosed by it.

FIGURE 2.01 William Watts’s clever use of nature to make spherical ball bearings.

Calculating the volume of a curved shape was a significant challenge, but he applied a cunning trick: slice the sphere with parallel cuts into many thin layers, and then approximate the layers by discs. Now, he knew the formula for the volume of a disc: it was just the area of the circle times the thickness of the disc. By adding together the volumes of all these different sized discs, Archimedes could get an approximation for the volume of the sphere.

FIGURE 2.02 A sphere can be approximated by stacking different sized discs on top of one another.

Then came the clever bit. If he made the discs thinner and thinner until they were infinitesimally thin, the formula would give an exact calculation of the volume. It was one of the first times that the idea of infinity was used in mathematics, and a similar technique would eventually become the basis for the mathematics of the calculus developed by Isaac Newton and Gottfried Leibniz nearly two thousand years later.

Archimedes went on to use this method to calculate the volumes of many different shapes. He was especially proud of the discovery that if you put a spherical ball inside a cylindrical tube of the same height, then the volume of the air in the tube is precisely half the volume of the ball. He was so excited by this that he insisted a cylinder and a sphere should be carved on his gravestone.

Although Archimedes had successfully found a method to calculate the volume and surface area of the sphere, he didn’t have the skills to prove his hunch that it is the most efficient shape in nature. Amazingly, it was not until 1884 that the mathematics became sophisticated enough for the German Hermann Schwarz to prove that there is no mysterious shape with less energy that could trump the sphere.

How to make the world’s roundest football

Many sports are played with spherical balls: tennis, cricket, snooker, football. Although nature is very good at making spheres, humans find it particularly tricky. This is because most of the time we make the balls by cutting shapes from flat sheets of material which then have to be either moulded or sewn together. In some sports a virtue is made of the fact that it’s hard to make spheres. A cricket ball consists of four moulded pieces of leather sewn together, and so isn’t truly spherical. The seam can be exploited by a bowler to create unpredictable behaviour as the ball bounces off the pitch.

In contrast, table-tennis players require balls that are perfectly spherical. The balls are made by fusing together two celluloid hemispheres, but the method is not very successful since over 95% are discarded. Ping-pong ball manufacturers have great fun sorting the spheres from the misshapen balls. A gun fires balls through the air, and any that aren’t spheres will swing to the left or to the right. Only those that are truly spherical fly dead straight and get collected on the other side of the firing range.

How, then, can we make the perfect sphere? In the build-up to the football World Cup in 2006 in Germany there were claims by manufacturers that they had made the world’s most spherical football. Footballs are very often constructed by sewing together flat pieces of leather, and many of the footballs that have been made over the generations are assembled from shapes that have been played with since ancient times. To find out how to make the most symmetrical football, we can start by exploring ‘balls’ built from a number of copies of a single symmetrical piece of leather, arranged so that the assembled solid shape is symmetrical. To make it as symmetrical as possible, the same number of faces should meet at each point of the shape. These are the shapes that Plato explored in his Timaeus, written in 360BC.

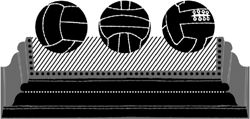
FIGURE 2.03 Some early designs for footballs.

What are the different possibilities for Plato’s footballs? The one requiring fewest components is made by sewing together four equilateral triangles to make a triangular-based pyramid called a tetrahedron—but this doesn’t make a very good football because there are so few faces. As we shall see in Chapter 3, this shape may not have made it onto the football pitch, but it does feature in other games that were played in the ancient world.

Another configuration is the cube, which is made of six square faces. At first sight this shape looks rather too stable for a football, but actually its structure underlies many of the early footballs. The very first World Cup football used in 1930 consisted of 12 rectangular strips of leather grouped in six pairs and arranged as if assembling a cube. Although now rather shrunken and unsymmetrical, one of these balls is on display at the National Museum of Football in Preston, in the North of England. Another rather extraordinary football that was also used in the 1930s is also based on the cube and has six H-shaped pieces cleverly interconnected.

Let’s go back to equilateral triangles. Eight of them can be arranged symmetrically to make an octahedron, effectively by fusing two square-based pyramids together. Once they are fused together, you can’t tell where the join is.

The more faces there are, the rounder Plato’s footballs are likely to be. The next shape in line after the octahedron is the dodecahedron, made from 12 pentagonal faces. There is an association here with the 12 months of the year, and ancient examples of these shapes have been discovered with calendars carved on their faces. But of all Plato’s shapes, it’s the icosahedron, made out of 20 equilateral triangles, that approximates best to a spherical football.

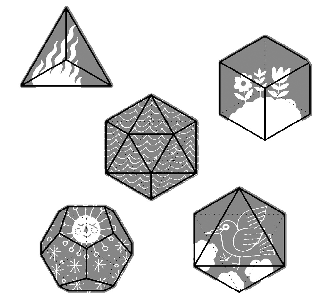
FIGURE 2.04 The Platonic solids were associated with the building blocks of nature.

Plato believed that together these five shapes were so fundamental that they were related to the four classical elements, the building blocks of nature: the tetrahedron, the spikiest of the shapes, was the shape of fire; the stable cube was associated with earth; the octahedron was air; and the roundest of the shapes, the icosahedron, was slippery water. The fifth shape, the dodecahedron, Plato decided represented the shape of the universe.

How can we be sure that there isn’t a sixth football Plato might have missed? It was another Greek mathematician, Euclid, who in the climax to one of the greatest mathematical books ever written proved that it’s impossible to sew together any other combinations of a single symmetrical shape to make a sixth football to add to Plato’s list. Called simply The Elements, Euclid’s book is probably responsible for founding the analytical art of logical proof in mathematics. The power of mathematics is that it can provide 100% certainty about the world, and Euclid’s proof tells us that, as far as these shapes go, we have seen everything—there really are no other surprises waiting out there that we’ve missed.

Make a goal out of card and see how good the different shapes are for finger football. Try some of the tricks in this video: http://bit.ly/Fingerfooty which you can also see by using your smartphone to scan this code.

How Archimedes improved on Plato’s footballs

What if you tried to smooth out some of the corners of Plato’s five footballs? If you took the 20-faced icosahedron and chopped off all the corners, then you might hope to get a rounder football. In the icosahedron, five triangles meet at each point, and if you chop off the corners you get pentagons. The triangles with their three corners cut off become hexagons, and this so-called truncated icosahedron is in fact the shape that has been used for footballs ever since it was first introduced in the 1970 World Cup finals in Mexico. But are there other shapes made from a variety of symmetrical patches that could make an even better football for the next World Cup?

It was in the third century BC that the Greek mathematician Archimedes set out to improve on Plato’s shapes. He started by looking at what happens if you use two or more different building blocks as the faces of your shape. The shapes still needed to fit neatly together, so the edges of each type of face had to be the same length. That way you’d get an exact match along the edge. He also wanted as much symmetry as possible, so all the vertices—the corners where the faces meet—had to look identical. If two triangles and two squares met at one corner of the shape, then this had to happen at every corner.

The world of geometry was forever on Archimedes’ mind. Even when his servants dragged a reluctant Archimedes from his mathematics to the baths to wash himself, he would spend his time drawing geometrical shapes in the embers of the chimney or in the oils on his naked body with his finger. Plutarch describes how ‘the delight he had in the study of geometry took him so far from himself that it brought him into a state of ecstasy’.

It was during these geometric trances that Archimedes came up with a complete classification of the best shapes for footballs, finding 13 different ways that such shapes could be put together. The manuscript in which Archimedes recorded his shapes has not survived, and it is only from the writings of Pappus of Alexandria, who lived some 500 years later, that we have any record of the discovery of these 13 shapes. They nonetheless go by the name of the Archimedean solids.

Some he created by cutting bits off the Platonic solids, like the classic football. For example, snip the four ends off a tetrahedron. The original triangular faces then turn into hexagons, while the faces revealed by the cuts are four new triangles. So four hexagons and four triangles can be put together to make something called a truncated tetrahedron (Figure 2.05).

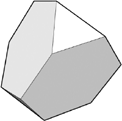
FIGURE 2.05

In fact, seven of the 13 Archimedean solids can be created by cutting bits off Platonic solids, including the classic football of pentagons and hexagons. More remarkable was Archimedes’ discovery of some of the other shapes. For example, it is possible to put together 30 squares, 20 hexagons and 12 ten-sided figures to make a symmetrical shape called a great rhombicosidodecahedron (Figure 2.06).

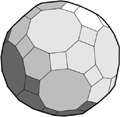
FIGURE 2.06

It was one of these 13 Archimedean solids that was behind the new Zeitgeist ball introduced at the World Cup in Germany in 2006 and heralded as the world’s roundest football. Made up of 14 curved pieces, the ball is actually structured around the truncated octahedron. Take the octahedron made up of eight equilateral triangles, and cut off the six vertices. The eight triangles become hexagons, and the six vertices are replaced by squares (Figure 2.07).

FIGURE 2.07

Perhaps future World Cups might feature one of the more exotic of Archimedes’ footballs. My choice would be the snub dodecahedron, made up of 92 symmetrical pieces—12 pentagons and 80 equilateral triangles (Figure 2.08).

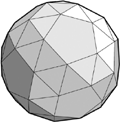
FIGURE 2.08

Pictures of all 13 Archimedean solids can be found at http://bit.ly/Archimedean or by using your smartphone to scan this code.

Even to the last, Archimedes’ mind was on things mathematical. In 212BC the Romans invaded his home of Syracuse. He was so engrossed in drawing diagrams to solve a mathematical conundrum that he was completely unaware of the fall of the city around him. When a Roman soldier burst into his rooms with sword brandished, Archimedes pleaded to at least be able to finish his calculations before he ran him through. ‘How can I leave this work in such an imperfect state?’ he cried. But the soldier was not prepared to wait for the QED, and hacked Archimedes down in mid-theorem.

What shape do you like your tea?

Shapes have become a hot issue not just for football manufacturers but also for the tea drinkers of England. For generations we were content with the simple square, but now teacups are swimming with circles, spheres and even pyramid-shaped tea bags in the nation’s drive to brew the ultimate cuppa.

The tea bag was invented by mistake at the beginning of the twentieth century by a New York tea merchant, Thomas Sullivan. He’d sent customers samples of tea in small silken bags, but rather than removing the tea from the bags, customers assumed they were meant to put the whole bag in the water. It took until the 1950s for the British to be convinced by such a radical change to their tea-drinking habits, but today it is estimated that over 100 million tea bags are dunked each day in the UK.

For years, the trusty square had allowed tea drinkers to make a cuppa without the hassle of having to wash out used tea leaves from teapots. The square is a very efficient shape—it was easy to make square tea bags, and there was no wastage of unused bits of bag material. For fifty years PG Tips, the leading manufacturer of tea bags, stamped out billions of tea bags a year in their factories up and down the country.

But in 1989, their main rival, Tetley, made a bold move to capture the market by changing the shape of the tea bag: they introduced circular bags. Although the change was little more than an aesthetic gimmick, it worked. Sales of the new shape soared. PG Tips realized that they had to go one better if they were to retain their customers. The circle might have excited punters, but it was still a flat, two-dimensional figure. So the team at PG decided to take a leap into the third dimension.

The PG Tips team knew that we are an impatient lot when it comes to our tea. On average, the bag stays in the cup for just 20 seconds before being hoisted out. If you cut open the average two-dimensional bag after it has been dunked for just 20 seconds you’ll find that the tea in the middle is completely dry, not having had time to get into contact with the water. The researchers at PG believed that a three-dimensional bag would behave like a mini teapot, giving all the leaves the chance to make contact with the water. They even enlisted a thermo-fluids expert from London University’s Imperial College to run computer models to confirm their belief in the power of the third dimension to improve the flavour of tea.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.