The Number Mysteries: A Mathematical Odyssey through Everyday Life

Some readers might recognize this sequence from Dan Brown’s novel The Da Vinci Code. They are in fact the first code that the hero has to crack on his way to the Holy Grail.

It isn’t only rabbits and Dan Brown who like these numbers. The number of petals on a flower is often a Fibonacci number. Trillium has three, a pansy has five, a delphinium has eight, marigolds have 13, chicory has 21, pyrethrum 34, and sunflowers often have 55 or even 89 petals. Some plants have flowers with twice a Fibonacci number of petals. These are plants, like some lilies, that are made up of two copies of a flower. And if your flower doesn’t have a Fibonacci number of petals, then that’s because a petal has fallen off … which is how mathematicians get round exceptions. (I don’t want to be inundated with letters from irate gardeners, so I’ll concede that there are a few exceptions which aren’t just examples of wilting flowers. For example, the starflower often has seven petals. Biology is never as perfect as mathematics.)

As well as in flowers, you can find the Fibonacci numbers running up and down pine cones and pineapples. Slice across a banana and you’ll find that it’s divided into 3 segments. Cut open an apple with a slice halfway between the stalk and the base, and you’ll see a 5-pointed star. Try the same with a Sharon fruit, and you’ll get an 8-pointed star. Whether it’s populations of rabbits or the structures of sunflowers or fruit, the Fibonacci numbers seem to crop up whenever there is growth happening.

The way shells evolve is also closely connected to these numbers. A baby snail starts off with a tiny shell, effectively a little one-by-one square house. As it outgrows its shell it adds another room to the house and repeats the process as it continues to grow. Since it doesn’t have much to go on, it simply adds a room whose dimensions are based on those of the two previous rooms, just as Fibonacci numbers are the sum of the previous two numbers. The result of this growth is a simple but beautiful spiral.

Actually these numbers shouldn’t be named after Fibonacci at all, because he was not the first to stumble across them. In fact they weren’t discovered by mathematicians at all, but by poets and musicians in medieval India. Indian poets and musicians were keen to explore all the possible rhythmic structures you can generate by using combinations of short and long rhythmic units. If a long sound is twice the length of a short sound, then how many different patterns are there with a set number of beats? For example, with eight beats you could do four long sounds or eight short ones. But there are lots of combinations between these two extremes.

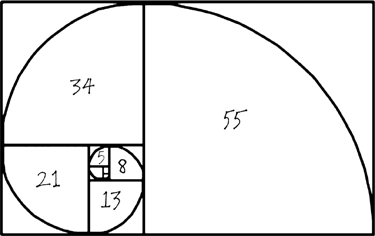
FIGURE 1.23 How to build a shell using Fibonacci numbers.

In the eighth century AD the Indian writer Virahanka took up the challenge to determine exactly how many different rhythms are possible. He discovered that as the number of beats goes up, the number of possible rhythmic patterns is given by the following sequence: 1, 2, 3, 5, 8, 13, 21, … He realized, just as Fibonacci did, that to get the next number in the sequence you simply add together the two previous numbers. So if you want to know how many possible rhythms there are with eight beats you go to the eighth number in the sequence, which is got by adding 13 and 21 to arrive at 34 different rhythmic patterns.

Perhaps it’s easier to understand the mathematics behind these rhythms than to try to follow the increasing population of Fibonacci’s rabbits. For example, to get the number of rhythms with eight beats you take the rhythms with six beats and add a long sound or take the rhythms with seven beats and add a short sound.

There is an intriguing connection between the Fibonacci sequence and the protagonists of this chapter, the primes. Look at the first few Fibonacci numbers:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Every pth Fibonacci number, where p is a prime number, is itself prime. For example, 11 is prime, and the 11th Fibonacci number is 89, a prime. If this always worked it would be a great way to generate bigger and bigger primes. Unfortunately it doesn’t. The 19th Fibonacci number is 4,181, and although 19 is prime, 4,181 is not: it equals 37×113. No mathematician has yet proved whether infinitely many Fibonacci numbers are prime numbers. This is another of the many unsolved prime number mysteries in mathematics.

How can you use rice and a chessboard to find primes?

Legend has it that chess was invented in India by a mathematician. The King was so grateful to the mathematician that he asked him to name any prize as a reward. The inventor thought for a minute, then asked for 1 grain of rice to be placed on the first square of the chessboard, 2 on the second, 4 on the third, 8 on the fourth, and so on, so that each square got twice as many grains of rice as were on the previous square.

The King readily agreed, astonished that the mathematician wanted so little—but he was in for a shock. When he began to place the rice on the board, the first few grains could hardly be seen. But by the time he’d got to the 16th square, he was already needing another kilogram of rice. By the 20th square, his servants had to bring in a wheelbarrow full. He never reached the 64th and last square on the board. By that point the total number of grains of rice on the board would have been a staggering

18,446,744,073,709,551,615

If we tried to repeat the feat at the heart of London, the pile of rice on the 64th square would stretch to the boundaries of the M25 and would be so high that it would cover all the buildings. In fact, there would be more rice in this pile than has been produced across the globe in the last millennium.

FIGURE 1.24 Repeated doubling makes numbers grow very quickly.

Not surprisingly, the King of India failed to give the mathematician the prize he had been promised and was forced into parting with half his fortune instead. That’s one way maths can make you rich.

But what has all this rice got to do with finding big prime numbers? Ever since the Greeks had proved that the primes go on for ever, mathematicians had been on the look-out for clever formulas that might generate bigger and bigger primes. One of the best of these formulas was discovered by a French monk called Marin Mersenne. Mersenne was a close friend of Pierre de Fermat and René Descartes, and he functioned like a seventeenth-century Internet hub, receiving letters from scientists all across Europe and communicating ideas to those he thought could develop them further.

His correspondence with Fermat led to the discovery of a powerful formula for finding huge primes. The secret of this formula is hidden inside the story of the rice and the chessboard. As you count up the grains of rice from the first square of the chessboard, the cumulative total quite often turns out to be a prime number. For example, after three squares there are 1+2+4=7 grains of rice, a prime number. By the fifth square there are 1+2+4+8+16=31 grains of rice.

Mersenne wondered whether it would turn out to be true that whenever you landed on a prime number square on the chessboard, the number of grains of rice up to that point might also be a prime. If it was, it would give you a way of generating bigger and bigger primes. Once you’d counted the prime number grains of rice, just move to this square on the chessboard and count the number of grains of rice up to this point, which Mersenne hoped would be an even bigger prime.

Unfortunately for Mersenne and for mathematics, his idea didn’t quite work. When you look on the 11th square of the chessboard, a prime number square, then up to that point there are a total of 2,047 grains of rice. Sadly, 2,047 is not prime—it equals 23×89. But although Mersenne’s idea didn’t always work, it has led to some of the largest prime numbers that have been discovered.

The Guinness Book of Primes

In the reign of Queen Elizabeth I, the largest known prime number was the number of grains of rice on the chessboard up to and including the 19th square: 524,287. By the time that Lord Nelson was fighting the Battle of Trafalgar, the record for the largest prime had gone up to the 31st square of the chessboard: 2,147,483,647. This ten-digit number was proved to be prime in 1772 by the Swiss mathematician Leonhard Euler, and it was the record-holder until 1867.

By 4 September 2006, the record had gone up to the number of grains of rice that would be on the 32,582,657th square, if we had a big enough chessboard. This new prime number has over 9.8 million digits, and it would take a month and a half to read it out loud. It was discovered not by some huge supercomputer but by an amateur mathematician using some software downloaded from the Internet.

The idea of this software is to utilize a computer’s idle time to do computations. The program it uses implements a clever strategy that was developed to test whether Mersenne’s numbers are prime. It still took a desktop computer several months to check Mersenne numbers with 9.8 million digits, but this is a lot faster than methods for testing whether a random number of this size is prime. By 2009, over ten thousand people had joined what has become known as the Great Internet Mersenne Prime Search, or GIMPS.

Be warned, though, that the search is not without its dangers. One GIMPS recruit worked for a telephone company in America and decided to enlist the help of 2,585 of the company’s computers in his search for Mersenne primes. The company began to get suspicious when its computers were taking five minutes rather than five seconds to retrieve telephone numbers.

If you want your computer to join the GIMPS, you can download the software at www.mersenne.org, or scan this code with your smartphone.

When the FBI eventually found the source of the slowdown, the employee owned up: ‘All that computational power was just too tempting for me,’ he admitted. The telephone company didn’t feel sympathetic to the pursuit of science, and fired the employee.

After September 2006, mathematicians were holding their breath to see when the record would pass the 10,000,000-digit barrier. The anticipation was not just for academic reasons—a prize of $100,000 was waiting for the person who got there first. The prize money was put up by the Electronic Frontier Foundation, a California-based organization that encourages collaboration and cooperation in cyberspace.

It was two more years before the record was broken. In a cruel twist of fate, two record-breaking primes were found within a few days of each other. The German amateur prime number sleuth Hans-Michael Elvenich must have thought he’d hit the jackpot when his computer announced on 6 September 2008 that it had just found a new Mersenne prime with 11,185,272 digits. But when he submitted his discovery to the authorities, his excitement turned to despair—he had been beaten to it by 14 days. On 23 August, Edson Smith’s computer in the maths department at UCLA had discovered an even bigger prime, with 12,978,189 digits. For the University of California at Los Angeles, breaking prime number records is nothing new. UCLA mathematician Raphael Robinson discovered five Mersenne primes in the 1950s, and two more were found by Alex Hurwitz at the beginning of the 1960s.

The developers of the program used by GIMPS agreed that the prize money shouldn’t simply go to the lucky person who was assigned that Mersenne number to check. $5,000 went to the developers of the software, $20,000 was shared among those who had broken records with the software since 1999, $25,000 was given to charity and the rest went to Edson Smith in California.

If you still want to win money by looking for primes, don’t worry about the fact that the 10,000,000-digit mark has been passed. For each new Mersenne prime found there is a prize of $3,000. But if it’s the big money you’re after, there is $150,000 on offer for passing 100 million digits and $200,000 if you can make it to the billion-digit mark. Thanks to the Ancient Greeks, we know that such record primes are waiting out there for someone to discover them. It’s just a matter of how much inflation will have eaten into the worth of these prizes before someone eventually claims the next one.

How to write a number with 12,978,189 digits

Edson Smith’s prime is phenomenally large. It would take over 3,000 pages of this book to record its digits, but luckily a bit of mathematics can produce a formula that expresses the number in a much more succinct manner.

The total number of grains of rice up to the Nth square of the chessboard is

R=1+2+4+8+…+2N–2+2N–1

Here’s a trick to find a formula for this number. It looks totally useless at first sight because it is so obvious: R=2R–R. How on earth can such an obvious equation help in calculating R? In mathematics it often helps to take a slightly different perspective, because then everything can suddenly look completely different.

Let’s first calculate 2R. That just means doubling all the terms in the big sum. But the point is that if you double the number of grains of rice on one square, the result is the same as the number grains on the next square along. So

2R=2+4+8+16+…+2N–1+2N

The next move is to subtract R. This will just knock out all the terms of 2R except the last one:

R=2R–R=(2+4+8+16+…+2N–1+2N)–(1+2+4+8+…+2N…2 +2N–1)

=(2+4+8+16+…+2N–1–)+2N–1–(2+4+8+…+2N–2+2N–1)

=2N–1

So the total number of grains of rice on the Nth square of the chess board is 2N–1, and this is the formula responsible for today’s record-breaking primes. By doubling enough times then taking 1 away from the answer you might just hope to hit a Mersenne prime, as primes found using this formula are called. To get Edson Smith’s 12,978,189-digit prime set N=43,112,609 in this formula.

How to cross the universe with a dragon noodle

Rice is not the only food associated with exploiting the power of doubling to create large numbers. Dragon noodles, or la mian noodles, are traditionally made by stretching the dough between your arms and then folding it back again to double the length. Each time you stretch the dough, the noodle becomes longer and thinner, but you need to work quickly because the dough dries out quickly, disintegrating into a noodly mess.

Cooks across Asia have competed for the accolade of doubling the noodle length the most times, and in 2001 the Taiwanese cook Chang Hun-yu managed to double his dough 14 times in two minutes. The noodle he ended up with was so thin that it could be passed through the eye of a needle. Such is the power of doubling that the noodle would have stretched from Mr Chang’s restaurant in the centre of the Taipei to the outskirts of the city, and when it was cut there were a total of 16,384 noodles.

This is the power of doubling, and it can very quickly lead to very big numbers. For example, if it were possible for Chang Hunyu to have carried on and doubled his noodle 46 times, the noodle would be the thickness of an atom and would be long enough to reach from Taipei to the outer reaches of our solar system. Doubling the noodle 90 times would get you from one side of the observable universe to the other. To get a sense of how big the current record prime number is, you would need to double the noodle 43,112,609 times and then take one noodle away to get the record prime discovered in 2008.

What are the odds that your telephone number is prime?

One of the geeky things that mathematicians always do is to check their telephone number to see whether it is prime. I moved house recently and needed to change my telephone number. I hadn’t had a prime telephone number at my previous house (house number 53, a prime) so I was hoping that at my new house (number 1, an ex-prime) I might be luckier.

The first number the phone company gave me looked promising, but when I put it into my computer and tested it I found that it was divisible by 7. ‘I’m not sure I’m going to remember that number … any chance of another number?’ The next number was also not prime—it was divisible by 3. (An easy test to see whether your number is divisible by 3: add up all the digits of your telephone number, and if the number you get is divisible by 3 then so is the original number.) After about three more attempts, the exasperated telephone company employee snapped: ‘Sir, I’m afraid I’m just going to give you the next number that comes up.’ Alas, I now have an even telephone number, of all things!

So what were the chances of me getting a prime telephone number? My number has eight digits. There is approximately a 1 in 17 chance that an eight-digit number is prime, but how does that probability change as the number of digits increases? For example, there are 25 primes under 100, which means that a number with two or fewer digits has a 1 in 4 chance of being prime. On average, as you count from 1 to 100 you get a prime every four numbers. But primes get rarer the higher you count.

The table below shows the changes in probability:

Primes get rarer and rarer, but they get rarer in a very regular way. Every time I add a digit, the probability decreases by about the same amount, 2.3, each time. The first person to notice this was a fifteen-year-old boy. His name was Carl Friedrich Gauss (1777–1855), and he would go on to become one of the greatest names in mathematics.

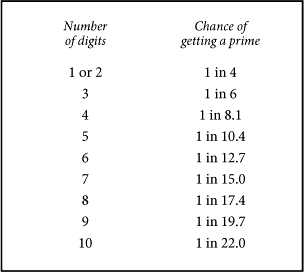
TABLE 1.2

Gauss made his discovery after being given a book of mathematical tables for his birthday which contained in the back a table of prime numbers. He was so obsessed with these numbers that he spent the rest of his life adding more and more figures to the tables in his spare time. Gauss was an experimental mathematician who liked to play around with data, and he believed that the way the primes thinned out would carry on in this uniform way however far you counted through the universe of numbers.

But how can you be sure that something strange won’t suddenly happen when you hit 100-digit numbers, or 1,000,000-digit numbers? Would the probability still be the same as adding on 2.3 for each new digit, or could the probabilities suddenly start behaving totally differently? Gauss believed that the pattern would always be there, but it took until 1896 for him to be vindicated. Two mathematicians, Jacques Hadamard and Charles de la Vallée Poussin, independently proved what is now called the prime number theorem: that the primes will always thin out in this uniform way.

Gauss’s discovery has led to a very powerful model which helps to predict a lot about the behaviour of prime numbers. It’s as if, to choose the primes, nature used a set of prime number dice with all sides blank except for one with a PRIME written on it:

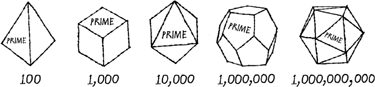
FIGURE 1.25 Nature’s prime number dice.

To decide whether each number is going to be prime, roll the dice. If it lands prime side up, then mark that number as prime; if it’s blank side up, the number isn’t prime. Of course, this is just a heuristic model—you can’t make 100 indivisible just by a roll of the dice. But it will give a set of numbers whose distribution is believed to be very like that of the primes. Gauss’s prime number theorem tells us how many sides there are on the dice. So for three-digit numbers, use a six-sided dice or a cube with one side prime. For four-digit numbers, an eight-sided dice—an octahedron. For five, digits a dice with 10.4 sides … of course, these are theoretical dice because there isn’t a polyhedron with 10.4 sides.

What’s the million-dollar prime problem?

The million-dollar question is about the nature of these dice: are the dice fair or not? Are the dice distributing the primes fairly through the universe of numbers, or are there regions where they are biased, sometimes giving too many primes, sometimes too few? The name of this problem is the Riemann Hypothesis.

Bernhard Riemann was a student of Gauss’s in the German city of Göttingen. He developed some very sophisticated mathematics which allows us to understand how these prime number dice are distributing the primes. Using something called a zeta function, special numbers called imaginary numbers and a fearsome amount of analysis, Riemann worked out the mathematics that controls the fall of these dice. He believed from his analysis that the dice would be fair, but he couldn’t prove it. To prove the Riemann Hypothesis, that is what you have to do.

Another way to interpret the Riemann Hypothesis is to compare the prime numbers to molecules of gas in a room. You may not know at any one instance where each molecule is, but the physics says that the molecules will be fairly evenly distributed around the room. There won’t be one corner with a concentration of molecules, and at another corner a complete vacuum. The Riemann Hypothesis would have the same implication for the primes. It doesn’t really help us to say where each particular prime can be found, but it does guarantee that they are distributed in a fair but random way through the universe of numbers. That kind of guarantee is often enough for mathematicians to be able to navigate the universe of numbers with a sufficient degree of confidence. However, until the million dollars is won, we’ll never be certain quite what the primes are doing as we count our way further into the never-ending reaches of the mathematical cosmos.

TWO

The Story of the Elusive Shape

The great seventeenth-century scientist Galileo Galilei once wrote:

The universe cannot be read until we have learnt the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word. Without these, one is wandering about in a dark labyrinth.

This chapter presents the A–Z of nature’s weird and wonderful shapes: from the six-pointed snowflake to the spiral of DNA, from the radial symmetry of a diamond to the complex shape of a leaf. Why are bubbles perfectly spherical? How does the body make such hugely complex shapes like the human lung? What shape is our universe? Mathematics is at the heart of understanding how and why nature makes such a variety of shapes, and it also gives us the power to create new shapes as well as the ability to say when there are no more shapes to be discovered.

It isn’t only mathematicians who are interested in shapes: architects, engineers, scientists and artists all want to understand how nature’s shapes work. They all rely on the mathematics of geometry. The Ancient Greek philosopher Plato put above his door a sign declaring: ‘Let no one ignorant of geometry enter here.’ In this chapter I want to give you a passport to Plato’s home, to the mathematical world of shapes. And at the end I’ll reveal another mathematical puzzle, one whose solution is worth another million dollars.

Why are bubbles spherical?