In your search for a secretary, there are two ways you can fail: stopping early and stopping late. When you stop too early, you leave the best applicant undiscovered. When you stop too late, you hold out for a better applicant who doesn’t exist. The optimal strategy will clearly require finding the right balance between the two, walking the tightrope between looking too much and not enough.

If your aim is finding the very best applicant, settling for nothing less, it’s clear that as you go through the interview process you shouldn’t even consider hiring somebody who isn’t the best you’ve seen so far. However, simply being the best yet isn’t enough for an offer; the very first applicant, for example, will of course be the best yet by definition. More generally, it stands to reason that the rate at which we encounter “best yet” applicants will go down as we proceed in our interviews. For instance, the second applicant has a 50/50 chance of being the best we’ve yet seen, but the fifth applicant only has a 1-in-5 chance of being the best so far, the sixth has a 1-in-6 chance, and so on. As a result, best-yet applicants will become steadily more impressive as the search continues (by definition, again, they’re better than all those who came before)—but they will also become more and more infrequent.

Okay, so we know that taking the first best-yet applicant we encounter (a.k.a. the first applicant, period) is rash. If there are a hundred applicants, it also seems hasty to make an offer to the next one who’s best-yet, just because she was better than the first. So how do we proceed?

Intuitively, there are a few potential strategies. For instance, making an offer the third time an applicant trumps everyone seen so far—or maybe the fourth time. Or perhaps taking the next best-yet applicant to come along after a long “drought”—a long streak of poor ones.

But as it happens, neither of these relatively sensible strategies comes out on top. Instead, the optimal solution takes the form of what we’ll call the Look-Then-Leap Rule: You set a predetermined amount of time for “looking”—that is, exploring your options, gathering data—in which you categorically don’t choose anyone, no matter how impressive. After that point, you enter the “leap” phase, prepared to instantly commit to anyone who outshines the best applicant you saw in the look phase.

We can see how the Look-Then-Leap Rule emerges by considering how the secretary problem plays out in the smallest applicant pools. With just one applicant the problem is easy to solve—hire her! With two applicants, you have a 50/50 chance of success no matter what you do. You can hire the first applicant (who’ll turn out to be the best half the time), or dismiss the first and by default hire the second (who is also best half the time).

Add a third applicant, and all of a sudden things get interesting. The odds if we hire at random are one-third, or 33%. With two applicants we could do no better than chance; with three, can we? It turns out we can, and it all comes down to what we do with the second interviewee. When we see the first applicant, we have no information—she’ll always appear to be the best yet. When we see the third applicant, we have no agency—we have to make an offer to the final applicant, since we’ve dismissed the others. But when we see the second applicant, we have a little bit of both: we know whether she’s better or worse than the first, and we have the freedom to either hire or dismiss her. What happens when we just hire her if she’s better than the first applicant, and dismiss her if she’s not? This turns out to be the best possible strategy when facing three applicants; using this approach it’s possible, surprisingly, to do just as well in the three-applicant problem as with two, choosing the best applicant exactly half the time.*

Enumerating these scenarios for four applicants tells us that we should still begin to leap as soon as the second applicant; with five applicants in the pool, we shouldn’t leap before the third.

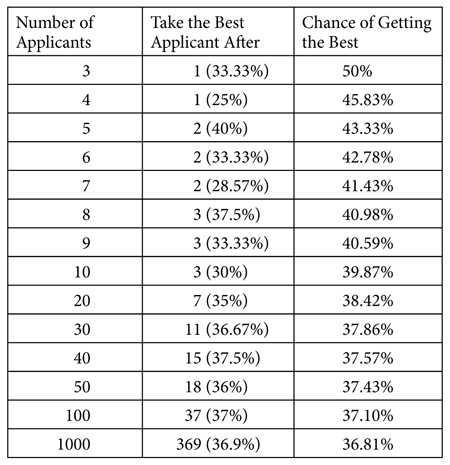
As the applicant pool grows, the exact place to draw the line between looking and leaping settles to 37% of the pool, yielding the 37% Rule: look at the first 37% of the applicants,* choosing none, then be ready to leap for anyone better than all those you’ve seen so far.

How to optimally choose a secretary.

As it turns out, following this optimal strategy ultimately gives us a 37% chance of hiring the best applicant; it’s one of the problem’s curious mathematical symmetries that the strategy itself and its chance of success work out to the very same number. The table above shows the optimal strategy for the secretary problem with different numbers of applicants, demonstrating how the chance of success—like the point to switch from looking to leaping—converges on 37% as the number of applicants increases.

A 63% failure rate, when following the best possible strategy, is a sobering fact. Even when we act optimally in the secretary problem, we will still fail most of the time—that is, we won’t end up with the single best applicant in the pool. This is bad news for those of us who would frame romance as a search for “the one.” But here’s the silver lining. Intuition would suggest that our chances of picking the single best applicant should steadily decrease as the applicant pool grows. If we were hiring at random, for instance, then in a pool of a hundred applicants we’d have a 1% chance of success, and in a pool of a million applicants we’d have a 0.0001% chance. Yet remarkably, the math of the secretary problem doesn’t change. If you’re stopping optimally, your chance of finding the single best applicant in a pool of a hundred is 37%. And in a pool of a million, believe it or not, your chance is still 37%. Thus the bigger the applicant pool gets, the more valuable knowing the optimal algorithm becomes. It’s true that you’re unlikely to find the needle the majority of the time, but optimal stopping is your best defense against the haystack, no matter how large.

Lover’s Leap

The passion between the sexes has appeared in every age to be so nearly the same that it may always be considered, in algebraic language, as a given quantity.

—THOMAS MALTHUS

I married the first man I ever kissed. When I tell this to my children they just about throw up.

—BARBARA BUSH

Before he became a professor of operations research at Carnegie Mellon, Michael Trick was a graduate student, looking for love. “It hit me that the problem has been studied: it is the Secretary Problem! I had a position to fill [and] a series of applicants, and my goal was to pick the best applicant for the position.” So he ran the numbers. He didn’t know how many women he could expect to meet in his lifetime, but there’s a certain flexibility in the 37% Rule: it can be applied to either the number of applicants or the time over which one is searching. Assuming that his search would run from ages eighteen to forty, the 37% Rule gave age 26.1 years as the point at which to switch from looking to leaping. A number that, as it happened, was exactly Trick’s age at the time. So when he found a woman who was a better match than all those he had dated so far, he knew exactly what to do. He leapt. “I didn’t know if she was Perfect (the assumptions of the model don’t allow me to determine that), but there was no doubt that she met the qualifications for this step of the algorithm. So I proposed,” he writes.

“And she turned me down.”

Mathematicians have been having trouble with love since at least the seventeenth century. The legendary astronomer Johannes Kepler is today perhaps best remembered for discovering that planetary orbits are elliptical and for being a crucial part of the “Copernican Revolution” that included Galileo and Newton and upended humanity’s sense of its place in the heavens. But Kepler had terrestrial concerns, too. After the death of his first wife in 1611, Kepler embarked on a long and arduous quest to remarry, ultimately courting a total of eleven women. Of the first four, Kepler liked the fourth the best (“because of her tall build and athletic body”) but did not cease his search. “It would have been settled,” Kepler wrote, “had not both love and reason forced a fifth woman on me. This one won me over with love, humble loyalty, economy of household, diligence, and the love she gave the stepchildren.”

“However,” he wrote, “I continued.”

Kepler’s friends and relations went on making introductions for him, and he kept on looking, but halfheartedly. His thoughts remained with number five. After eleven courtships in total, he decided he would search no further. “While preparing to travel to Regensburg, I returned to the fifth woman, declared myself, and was accepted.” Kepler and Susanna Reuttinger were wed and had six children together, along with the children from Kepler’s first marriage. Biographies describe the rest of Kepler’s domestic life as a particularly peaceful and joyous time.

Both Kepler and Trick—in opposite ways—experienced firsthand some of the ways that the secretary problem oversimplifies the search for love. In the classical secretary problem, applicants always accept the position, preventing the rejection experienced by Trick. And they cannot be “recalled” once passed over, contrary to the strategy followed by Kepler.

In the decades since the secretary problem was first introduced, a wide range of variants on the scenario have been studied, with strategies for optimal stopping worked out under a number of different conditions. The possibility of rejection, for instance, has a straightforward mathematical solution: propose early and often. If you have, say, a 50/50 chance of being rejected, then the same kind of mathematical analysis that yielded the 37% Rule says you should start making offers after just a quarter of your search. If turned down, keep making offers to every best-yet person you see until somebody accepts. With such a strategy, your chance of overall success—that is, proposing and being accepted by the best applicant in the pool—will also be 25%. Not such terrible odds, perhaps, for a scenario that combines the obstacle of rejection with the general difficulty of establishing one’s standards in the first place.

Kepler, for his part, decried the “restlessness and doubtfulness” that pushed him to keep on searching. “Was there no other way for my uneasy heart to be content with its fate,” he bemoaned in a letter to a confidante, “than by realizing the impossibility of the fulfillment of so many other desires?” Here, again, optimal stopping theory provides some measure of consolation. Rather than being signs of moral or psychological degeneracy, restlessness and doubtfulness actually turn out to be part of the best strategy for scenarios where second chances are possible. If you can recall previous applicants, the optimal algorithm puts a twist on the familiar Look-Then-Leap Rule: a longer noncommittal period, and a fallback plan.

For example, assume an immediate proposal is a sure thing but belated proposals are rejected half the time. Then the math says you should keep looking noncommittally until you’ve seen 61% of applicants, and then only leap if someone in the remaining 39% of the pool proves to be the best yet. If you’re still single after considering all the possibilities—as Kepler was—then go back to the best one that got away. The symmetry between strategy and outcome holds in this case once again, with your chances of ending up with the best applicant under this second-chances-allowed scenario also being 61%.

For Kepler, the difference between reality and the classical secretary problem brought with it a happy ending. In fact, the twist on the classical problem worked out well for Trick, too. After the rejection, he completed his degree and took a job in Germany. There, he “walked into a bar, fell in love with a beautiful woman, moved in together three weeks later, [and] invited her to live in the United States ‘for a while.’” She agreed—and six years later, they were wed.

Knowing a Good Thing When You See It: Full Information

The first set of variants we considered—rejection and recall—altered the classical secretary problem’s assumptions that timely proposals are always accepted, and tardy proposals, never. For these variants, the best approach remained the same as in the original: look noncommittally for a time, then be ready to leap.

But there’s an even more fundamental assumption of the secretary problem that we might call into question. Namely, in the secretary problem we know nothing about the applicants other than how they compare to one another. We don’t have an objective or preexisting sense of what makes for a good or a bad applicant; moreover, when we compare two of them, we know which of the two is better, but not by how much. It’s this fact that gives rise to the unavoidable “look” phase, in which we risk passing up a superb early applicant while we calibrate our expectations and standards. Mathematicians refer to this genre of optimal stopping problems as “no-information games.”

This setup is arguably a far cry from most searches for an apartment, a partner, or even a secretary. Imagine instead that we had some kind of objective criterion—if every secretary, for instance, had taken a typing exam scored by percentile, in the fashion of the SAT or GRE or LSAT. That is, every applicant’s score will tell us where they fall among all the typists who took the test: a 51st-percentile typist is just above average, a 75th-percentile typist is better than three test takers out of four, and so on.

Suppose that our applicant pool is representative of the population at large and isn’t skewed or self-selected in any way. Furthermore, suppose we decide that typing speed is the only thing that matters about our applicants. Then we have what mathematicians call “full information,” and everything changes. “No buildup of experience is needed to set a standard,” as the seminal 1966 paper on the problem put it, “and a profitable choice can sometimes be made immediately.” In other words, if a 95th-percentile applicant happens to be the first one we evaluate, we know it instantly and can confidently hire her on the spot—that is, of course, assuming we don’t think there’s a 96th-percentile applicant in the pool.

And there’s the rub. If our goal is, again, to get the single best person for the job, we still need to weigh the likelihood that there’s a stronger applicant out there. However, the fact that we have full information gives us everything we need to calculate those odds directly. The chance that our next applicant is in the 96th percentile or higher will always be 1 in 20, for instance. Thus the decision of whether to stop comes down entirely to how many applicants we have left to see. Full information means that we don’t need to look before we leap. We can instead use the Threshold Rule, where we immediately accept an applicant if she is above a certain percentile. We don’t need to look at an initial group of candidates to set this threshold—but we do, however, need to be keenly aware of how much looking remains available.

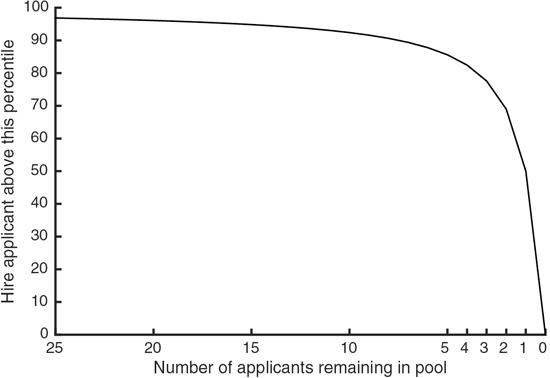
The math shows that when there are a lot of applicants left in the pool, you should pass up even a very good applicant in the hopes of finding someone still better than that—but as your options dwindle, you should be prepared to hire anyone who’s simply better than average. It’s a familiar, if not exactly inspiring, message: in the face of slim pickings, lower your standards. It also makes clear the converse: with more fish in the sea, raise them. In both cases, crucially, the math tells you exactly by how much.

The easiest way to understand the numbers for this scenario is to start at the end and think backward. If you’re down to the last applicant, of course, you are necessarily forced to choose her. But when looking at the next-to-last applicant, the question becomes: is she above the 50th percentile? If yes, then hire her; if not, it’s worth rolling the dice on the last applicant instead, since her odds of being above the 50th percentile are 50/50 by definition. Likewise, you should choose the third-to-last applicant if she’s above the 69th percentile, the fourth-to-last applicant if she’s above the 78th, and so on, being more choosy the more applicants are left. No matter what, never hire someone who’s below average unless you’re totally out of options. (And since you’re still interested only in finding the very best person in the applicant pool, never hire someone who isn’t the best you’ve seen so far.)

The chance of ending up with the single best applicant in this full-information version of the secretary problem comes to 58%—still far from a guarantee, but considerably better than the 37% success rate offered by the 37% Rule in the no-information game. If you have all the facts, you can succeed more often than not, even as the applicant pool grows arbitrarily large.

Optimal stopping thresholds in the full-information secretary problem.

The full-information game thus offers an unexpected and somewhat bizarre takeaway. Gold digging is more likely to succeed than a quest for love. If you’re evaluating your partners based on any kind of objective criterion—say, their income percentile—then you’ve got a lot more information at your disposal than if you’re after a nebulous emotional response (“love”) that might require both experience and comparison to calibrate.

Of course, there’s no reason that net worth—or, for that matter, typing speed—needs to be the thing that you’re measuring. Any yardstick that provides full information on where an applicant stands relative to the population at large will change the solution from the Look-Then-Leap Rule to the Threshold Rule and will dramatically boost your chances of finding the single best applicant in the group.

There are many more variants of the secretary problem that modify its other assumptions, perhaps bringing it more in line with the real-world challenges of finding love (or a secretary). But the lessons to be learned from optimal stopping aren’t limited to dating or hiring. In fact, trying to make the best choice when options only present themselves one by one is also the basic structure of selling a house, parking a car, and quitting when you’re ahead. And they’re all, to some degree or other, solved problems.

When to Sell

If we alter two more aspects of the classical secretary problem, we find ourselves catapulted from the realm of dating to the realm of real estate. Earlier we talked about the process of renting an apartment as an optimal stopping problem, but owning a home has no shortage of optimal stopping either.

Imagine selling a house, for instance. After consulting with several real estate agents, you put your place on the market; a new coat of paint, some landscaping, and then it’s just a matter of waiting for the offers to come in. As each offer arrives, you typically have to decide whether to accept it or turn it down. But turning down an offer comes at a cost—another week (or month) of mortgage payments while you wait for the next offer, which isn’t guaranteed to be any better.

Selling a house is similar to the full-information game. We know the objective dollar value of the offers, telling us not only which ones are better than which, but also by how much. What’s more, we have information about the broader state of the market, which enables us to at least roughly predict the range of offers to expect. (This gives us the same “percentile” information about each offer that we had with the typing exam above.) The difference here, however, is that our goal isn’t actually to secure the single best offer—it’s to make the most money through the process overall. Given that waiting has a cost measured in dollars, a good offer today beats a slightly better one several months from now.

Having this information, we don’t need to look noncommittally to set a threshold. Instead, we can set one going in, ignore everything below it, and take the first option to exceed it. Granted, if we have a limited amount of savings that will run out if we don’t sell by a certain time, or if we expect to get only a limited number of offers and no more interest thereafter, then we should lower our standards as such limits approach. (There’s a reason why home buyers look for “motivated” sellers.) But if neither concern leads us to believe that our backs are against the wall, then we can simply focus on a cost-benefit analysis of the waiting game.

Here we’ll analyze one of the simplest cases: where we know for certain the price range in which offers will come, and where all offers within that range are equally likely. If we don’t have to worry about the offers (or our savings) running out, then we can think purely in terms of what we can expect to gain or lose by waiting for a better deal. If we decline the current offer, will the chance of a better one, multiplied by how much better we expect it to be, more than compensate for the cost of the wait? As it turns out, the math here is quite clean, giving us an explicit function for stopping price as a function of the cost of waiting for an offer.

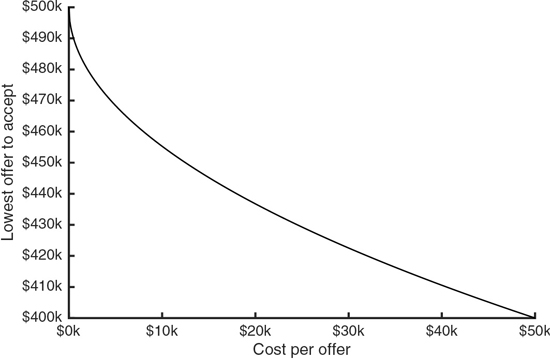
This particular mathematical result doesn’t care whether you’re selling a mansion worth millions or a ramshackle shed. The only thing it cares about is the difference between the highest and lowest offers you’re likely to receive. By plugging in some concrete figures, we can see how this algorithm offers us a considerable amount of explicit guidance. For instance, let’s say the range of offers we’re expecting runs from $400,000 to $500,000. First, if the cost of waiting is trivial, we’re able to be almost infinitely choosy. If the cost of getting another offer is only a dollar, we’ll maximize our earnings by waiting for someone willing to offer us $499,552.79 and not a dime less. If waiting costs $2,000 an offer, we should hold out for an even $480,000. In a slow market where waiting costs $10,000 an offer, we should take anything over $455,279. Finally, if waiting costs half or more of our expected range of offers—in this case, $50,000—then there’s no advantage whatsoever to holding out; we’ll do best by taking the very first offer that comes along and calling it done. Beggars can’t be choosers.

Optimal stopping thresholds in the house-selling problem.

The critical thing to note in this problem is that our threshold depends only on the cost of search. Since the chances of the next offer being a good one—and the cost of finding out—never change, our stopping price has no reason to ever get lower as the search goes on, regardless of our luck. We set it once, before we even begin, and then we quite simply hold fast.

The University of Wisconsin–Madison’s Laura Albert McLay, an optimization expert, recalls turning to her knowledge of optimal stopping problems when it came time to sell her own house. “The first offer we got was great,” she explains, “but it had this huge cost because they wanted us to move out a month before we were ready. There was another competitive offer … [but] we just kind of held out until we got the right one.” For many sellers, turning down a good offer or two can be a nerve-racking proposition, especially if the ones that immediately follow are no better. But McLay held her ground and stayed cool. “That would have been really, really hard,” she admits, “if I didn’t know the math was on my side.”

This principle applies to any situation where you get a series of offers and pay a cost to seek or wait for the next. As a consequence, it’s relevant to cases that go far beyond selling a house. For example, economists have used this algorithm to model how people look for jobs, where it handily explains the otherwise seemingly paradoxical fact of unemployed workers and unfilled vacancies existing at the same time.

In fact, these variations on the optimal stopping problem have another, even more surprising property. As we saw, the ability to “recall” a past opportunity was vital in Kepler’s quest for love. But in house selling and job hunting, even if it’s possible to reconsider an earlier offer, and even if that offer is guaranteed to still be on the table, you should nonetheless never do so. If it wasn’t above your threshold then, it won’t be above your threshold now. What you’ve paid to keep searching is a sunk cost. Don’t compromise, don’t second-guess. And don’t look back.

<1 2 3 >

На страницу:

Перейти

2 из 3