Теория и практика распознавания инженерных сооружений, промышленных предприятий и объектов железнодорожного транспорта при дешифрировании аэроснимков

Основой ИНС является искусственный нейрон, который является отдаленным подобием биологического нейрона (рисунок 2.3).

Рисунок 2.3 – Упрощение от биологического нейрона к искусственному нейрону

Искусственный нейрон имеет несколько входов (аналоги синапсов в биологическом нейроне) и один выход (аналог аксона).

Математически нейрон выполняет функцию суммирования S входных сигналов Х с учетом их весов W, и затем результат обрабатывается функцией активации F. Результат на выходе Y зависит от входных сигналов X и их весов W, а также от функции активации. Коэффициенты W являются элементами памяти нейрона и основными элементами обучения нейронной сети.

Функция активации ограничивает амплитуду выходного сигнала нейрона. Обычно нормализованный диапазон амплитуд выходного сигнала нейрона лежит в интервале [0, 1] или [-1, 1].

На вход функции активации подается сумма всех произведений сигналов и весов этих сигналов.

Наиболее часто используемыми функциями (рисунок 2.4) активации являются:

1. Пороговая функция. Это простая кусочно-линейная функция. Если входное значение меньше порогового, то значение функции активации равно минимальному допустимому, иначе – максимально допустимому.

2. Линейный порог. Это несложная кусочно-линейная функция. Имеет два линейных участка, где функция активации тождественно равна минимально допустимому и максимально допустимому значению и есть участок, на котором функция строго монотонно возрастает.

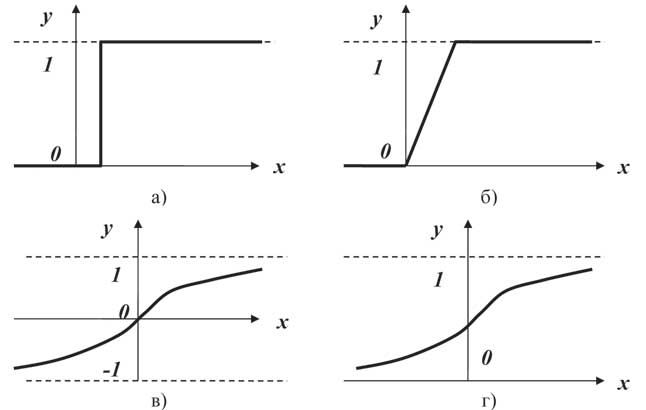
Рисунок 2.4 – Типы функции активации нейрона: а) функция единичного скачка; б) функция единичного скачка с линейным порогом; в) гиперболический тангенс у=th(x); г) функция сигмоида у=1/(1+exp(-ax))

3. Сигмоидальная функция, или сигмоида. Это монотонно возрастающая дифференцируемая S-образная нелинейная функция. Сигмоида позволяет усиливать слабые сигналы и не насыщаться от сильных сигналов.

4. Гиперболический тангенс. Эта функция принимает на входе произвольное вещественное число, а на выходе дает вещественное число в интервале от –1 до 1. Подобно сигмоиде, гиперболический тангенс может насыщаться. Однако, в отличие от сигмоиды, выход данной функции центрирован относительно нуля.

Объединение искусственных нейронов в группу формирует нейронную сеть (рисунок 2.5).

Рисунок 2.5 – Схема формирования нейронной сети

Слой нейронной сети – это множество нейронных элементов, на которые в каждый такт времени параллельно поступает информация от других нейронных элементов сети.

Простая нейронная сеть состоит из входного слоя, скрытого слоя и выходного слоя. Сети, содержащие много скрытых слоев, часто называют глубинными нейронными сетями.

2.6. Топология искусственных нейронных сетей

Среди основных топологий нейронных сетей можно выделить полносвязные, сверточные и рекуррентные нейронные сети.

Полносвязные нейронные сети имеют несколько слоев, которые связаны между собой таким образом, что каждый нейрон последующего слоя имеет связь со всеми нейронами предыдущего слоя. Сложность сети резко возрастает от увеличения размерности входных данных и от количества скрытых слоев. Так, для анализа изображения форматом 28×28 элементов потребуется 784 нейрона в скрытом слое, и каждый из них должен иметь 784 входа для соединения с предыдущим слоем. Другая проблема заключается в том, что в полносвязной сети изображения представляют собой одномерные последовательности и при этом не учитываются особенности изображений как структуры данных. Тем не менее, для изображений небольших форматов можно использовать и полносвязную сеть.

Сверточные нейронные сети предназначены для обработки двумерных структур данных, прежде всего изображений. Сверточная сеть представляет собой комбинацию трех типов слоев:

– слои, которые выполняют функцию свертки над двумерными массивами данных (сверточные слои),

– слои, выполняющие функцию уменьшения формата данных (слой субдискретизации),

– полносвязные слои, завершающие процесс обработки данных.

Структура сверточных нейронных сетей принципиально многослойная. Работа сверточной нейронной сети обычно интерпретируется как переход от конкретных особенностей изображения к более абстрактным деталям и далее к еще более абстрактным деталям вплоть до выделения понятий высокого уровня. При этом сеть самонастраивается и вырабатывает необходимую иерархию абстрактных признаков (последовательности карт признаков), фильтруя маловажные детали и выделяя существенное. Примером классической сверточной нейронной сети является сеть VGG16 (рисунок 2.6).

Рисунок 2.6 – Структура классической сети VGG16

Сеть VGG-16 имеет 16 слоев и способна работать с изображениями достаточно большого формата 224×224 пикселя. В своей стандартной топологии эта сеть способна работать с датасетом изображений ImageNet, содержащим более 15 млн изображений, разбитых на 22000 категорий.

Рекуррентные нейронные сети отличаются от многослойных сетей тем, что могут использовать свою внутреннюю память для обработки последовательностей произвольной длины. Благодаря направленной последовательности связей между элементами рекуррентных сетей они применимы в таких задачах, где нечто целостное разбито на сегменты, например, распознавание рукописного текста или распознавание речи.

2.7. Обучение искусственных нейронных сетей

Для работы с нейронными сетями требуется их обучение под конкретную задачу. В частности, для решения задачи распознавания объектов на изображении требуется обучение сети по специально подготовленному набору данных, который содержит изображения всех классов распознаваемых объектов, сгруппированных в соответствующие разделы. Такой тип данных носит название датасет (набор данных, Data set).

Существует большое количество уже собранных и подготовленных датасетов для решения различных задач с использованием нейронных сетей (не только для задач распознавания объектов). Более того, существуют уже заранее обученные под решение конкретной задачи нейронные сети, которые можно взять в готовом виде. Но перечень таких сетей и датасетов не очень большой, и в общем случае перед разработчиком может стоять задача выбора конфигурации нейронной сети под конкретную задачу и создание соответствующей базы данных (датасета) для ее обучения.

Формирование датасета является наиболее трудоемкой частью процесса разработки, поэтому в первую очередь нужно проверить возможное наличие похожего датасета на доступных ресурсах. На этом ресурсе имеется более 50000 свободно распространяемых датасетов и более 400000 примеров реализаций нейронных сетей. В ряде случаев имеющиеся датасеты можно объединять, модифицировать и дополнять.

Процесс обучения нейронных сетей представляет собой сложный процесс обработки данных, который включает в себя последовательное предъявление данных на вход нейронной сети и сравнение выходных данных с их истинным значением, после чего вносится коррекция весовых коэффициентов нейронов в сторону уменьшения ошибки выходных данных. Этот процесс производится многократно с использованием данных из датасета. В процессе обучения используется часть датасета, которая носит название тренировочный набор. При этом данные из датасета могут предъявляться последовательно несколько раз.

К общим рекомендациям состава датасета относятся увеличение количества изображений с отмеченными целевыми объектами, а также включение в датасет изображений с возможными вариантами фона (частей изображения, не относящихся к целевым объектам). Большие по размерам и общему объему изображения увеличивают время обучения и работы классификатора. Для каждой сетевой модели рекомендуется подавать на вход изображения различных размеров. В экспериментах было установлено, что обучение сети на изображениях, повернутых относительно исходных на 90°, производится быстрее, чем на изображениях исходной видеопоследовательности.

Один цикл обучения с использованием всего датасета носит название эпоха. Как правило, для качественного обучения сети требуется много эпох. Процесс обучения нейронных сетей, имеющих много скрытых слоев, часто носит название глубокого обучения.

Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети. Затем по определенному правилу вычисляется ошибка, и происходит изменение весовых коэффициентов связей внутри сети в зависимости от выбранного алгоритма. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня (рисунок 2.7).

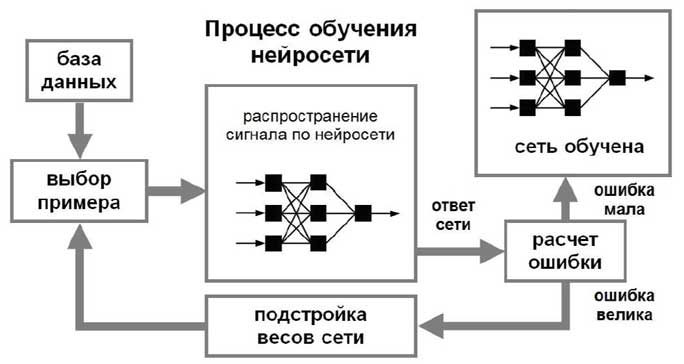
Рисунок 2.7 – Схема обучения нейронной сети

При обучении без учителя обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью. Для обучения нейронных сетей без учителя применяются сигнальные метод обучения Хебба и Ойа.

Математически процесс обучения можно описать следующим образом. В процессе функционирования нейронная сеть формирует выходной сигнал Y, реализуя некоторую функцию Y=G(X). Если архитектура сети задана, то вид функции G определяется значениями синаптических весов и смещенной сети.

Пусть решением некоторой задачи является функция Y=F(X), заданная параметрами входных-выходных данных (X1, Y1), (X2, Y2), …, (XN, YN), для которых Yk=F(Xk), где k=1, 2, …, N.

Обучение состоит в поиске (синтезе) функции G, близкой к F в смысле некоторой функции ошибки E.

Если выбрано множество обучающих примеров – пар (XN, YN), где k=1, 2, …, N) и способ вычисления функции ошибки E, то обучение нейронной сети превращается в задачу многомерной оптимизации, имеющую очень большую размерность, при этом, поскольку функция E может иметь произвольный вид, обучение в общем случае – многоэкстремальная невыпуклая задача оптимизации.

Для решения этой задачи могут использоваться следующие (итерационные) алгоритмы:

1. Алгоритмы локальной оптимизации с вычислением частных производных первого порядка:

градиентный алгоритм (метод наискорейшего спуска),

методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента,

метод сопряженных градиентов,

методы, учитывающие направление антиградиента на нескольких шагах алгоритма.

2. Алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка:

метод Ньютона,

методы оптимизации с разреженными матрицами Гессе,

квазиньютоновские методы,

метод Гаусса – Ньютона,

метод Левенберга – Марквардта и др.

3. Стохастические алгоритмы оптимизации:

поиск в случайном направлении,

имитация отжига,

метод Монте-Карло (численный метод статистических испытаний).

4. Алгоритмы глобальной оптимизации (задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция).

2.8. Алгоритм обучения однослойного нейрона

Обучение нейронной сети в задачах классификации происходит на наборе обучающих примеров X(1), X(2), …, X(Р), в которых ответ – принадлежность к классу А или B – известен. Определим индикатор D следующим образом: положим D(X)=1, если X из класса А, и положим D(X)=0, если X из класса B, то есть

где всякий вектор X состоит из n компонент: X=(x1, x2 …., xn).

Задача обучения персептрона состоит в нахождении таких параметров w1, w2, …, wn и h, что на каждом обучающем примере персептрон выдавал бы правильный ответ, то есть

Если персептрон обучен на большом числе корректно подобранных примеров и равенство (2.2) выполнено для почти всех X(i),i=1,Р, то в дальнейшем персептрон будет с близкой к единице вероятностью проводить правильную классификацию для остальных примеров. Этот интуитивно очевидный факт был впервые математически доказан (при некоторых предположениях) в основополагающей работе наших соотечественников В. Вапника и А. Червоненскиса еще в 1960-х годах.

На практике, однако, оценки по теории Вапника – Червоненскиса иногда не очень удобны, особенно для сложных моделей нейронных сетей. Поэтому практически, чтобы оценить ошибку классификации, часто поступают следующим образом: множество обучающих примеров разбивают на два случайно выбранных подмножества, при этом обучение идет на одном множестве, а проверка обученного персептрона – на другом.

Рассмотрим подробнее алгоритм обучения персептрона.

Шаг 1. Инициализация синаптических весов и смещения.

Значения всех синаптических весов модели полагают равными нулю: wi=0, i=1,n; смещение нейрона h устанавливают равны некоторому малому случайному числу. Ниже, из соображений удобства изложения и проведения операций будем пользоваться обозначением w0= —h.

Обозначим через wi(t), i=1,n вес связи от i-го элемента входного сигнала к нейрону в момент времени t.

Шаг 2. Предъявление сети нового входного и желаемого выходного сигналов.

Входной сигнал X=(x1, x2 …., xn) предъявляется нейрону вместе с желаемым выходным сигналом D.

Шаг 3. Адаптация (настройка) значений синаптических весов. Вычисление выходного сигнала нейрона.

Перенастройка (адаптация) синаптических весов проводится по следующей формуле:

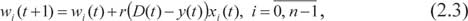
где D(t) – индикатор, определенный равенством (2.1), а r – параметр обучения, принимающий значения меньшие 1.

Описанный выше алгоритм – это алгоритм градиентного спуска, который ищет параметры, чтобы минимизировать ошибку. Алгоритм итеративный. Формула итераций выводится следующим образом.

Введем риск

где суммирование идет по числу опытов (t – номер опыта), при этом задано максимальное число опытов – Т.

Подставим вместо F формулу для персептрона, вычислим градиент по w. В результате мы получим указанную выше формулу перенастройки весов.

В процессе обучения вычисляется ошибка δ(t)=D(t) – y(t).

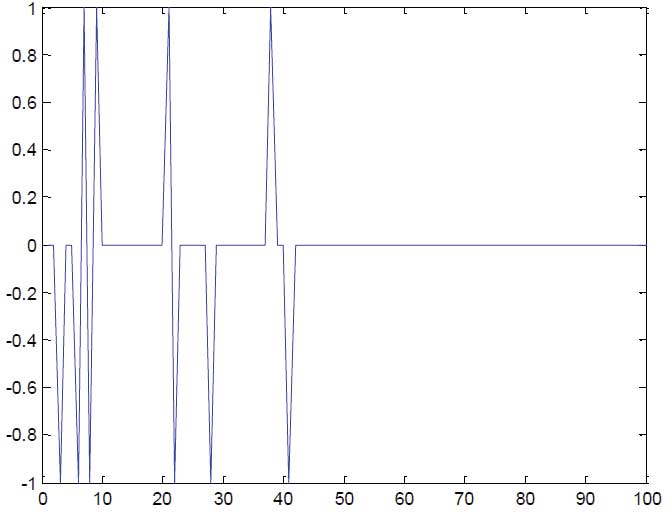
Рисунок 2.8 – График изменения ошибки в процессе обучения нейросети

На рисунке 2.8 изображен график, показывающий, как меняется ошибка в ходе обучения сети и адаптации весов. На нем хорошо видно, что, начиная с некоторого шага, величина δ(t) равна нулю. Это означает, что персептрон обучен.

2.9. Дешифрирование объектов с помощью технологий искусственного интеллекта

При автоматизированном (автоматическом) дешифрировании изображений решаются задачи, которые по классификации Гонсалеса и Вудса делятся на задачи высокого и низкого уровня. К задачам высокого уровня относятся:

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.